インスタントンとトンネル効果 (2) : 二重井戸型ポテンシャルにおけるインスタントン

※本記事は インスタントンとトンネル効果 (1) : 経路積分とWKB近似 の続きです。

今回は二重井戸型ポテンシャルにおける基底状態のエネルギー$E_0$の評価法について書きます。この系にはEuclid空間における古典解であるインスタントン解が存在します。この解による分配関数を用い、WKB近似における$E_0$の表式を求めます。

具体的なインスタントン分配関数の計算は次回行います。

本記事はRef.Sakitaに基づきます。またこの話題に関してはRef.Colemanが有名ですので文献として載せておきます。

二重井戸型ポテンシャルにおけるインスタントン

次の量子系を考えます（質量は1にしている）：
\begin{align} L&=\frac{1}{2}\dot q^2-V(q), \ \ V(q)=\frac{1}{g^2}U(gq)\\ &U(x)=\frac{\omega^2}{8a^2}(x^2-a^2)^2 \end{align}
ポテンシャル$V(a)$は以下のような形をしています（図1左）：

二重井戸型ポテンシャル。$g$が小さくなると最小点を隔てるポテンシャル障壁が大きくなる

このポテンシャルは$g\to 0$において$q=0$でのポテンシャル障壁が無限に高くなり、2つの独立した無限に深い井戸の系になります（図1右）。この場合のエネルギー準位は簡単に求めることができます。$q=a/g+\tilde q$として$q\sim a/g$でのポテンシャルは$g\to 0$のとき
\begin{align} V(q\sim a/g)\sim g^2\frac{\omega^2}{8a^2}\frac{4a^2}{g^2}\tilde q^2=\frac{1}{2}\omega^2\tilde q^2 \end{align}
です。これは調和振動子のポテンシャルであり、エネルギー準位は
\begin{align} E_n=\hbar \omega(n+1/2) \end{align}
となります。すなわち$g\to 0$では、$q=\pm a/g$に周期$\omega$の調和振動子が独立に存在します。よってこの極限における基底状態のエネルギー$E_0$は
\begin{align} E_0=\frac{1}{2}\hbar\omega \end{align}
であり、二重縮退しています。

しかし$g$が有限のとき、実際には$x=\pm a$付近の波動関数はトンネル効果で双方に漏れ出し、これによりエネルギーの縮退が解けます。以下、この基底状態のエネルギーをインスタントン解を用いてWKB近似で求めます。

基底状態のエネルギーの求め方

ここでは$E_0$の計算を以下のように行います。次の量
\begin{align} Z(\beta)=e^{-W(\beta)}:=\sum_n e^{-\beta E_n} \end{align}
を導入します。このとき
\begin{align} W(\beta)=-\ln\left(\sum_n e^{-\beta E_n}\right) \end{align}
ですが、$\beta\to +\infty$のとき、カッコ内の$\exp$の和は$E_0$の寄与で支配されます。よって
\begin{align} \lim_{\beta\to +\infty}W(\beta)=\beta E_0 \end{align}
ゆえに
\begin{align} E_0=\lim_{\beta\to +\infty}\frac{1}{\beta}W(\beta) \end{align}
です。ここで$Z(\beta)$は虚時間における分配関数であり、経路積分で以下のように表されます（Appendix参照）：
\begin{align} Z(\beta)&=\int {\cal D}q(\tau)\exp \left[ -\int^\beta_0\left(\frac{\dot q^2}{2}+V(q)\right)d\tau \right]\\ &=\text{const}\int{\cal D}x \exp \left[ -\frac{1}{g^2}\int_0^\beta d\tau \left( \frac{\dot x^2}{2}+U(x) \right) \right] \tag{1}\label{partfunc} \end{align}
前回の記事 より、$g^2$は$\hbar$と同じ役割を担っており、$g\to 0$のときWKB近似が使えることがわかります。WKB近似では$V$ではなく$U$で議論することに注意してください。

インスタントン解

$g\to 0$におけるWKB近似を用いるために、$Z(\beta)$に寄与する古典解を求めます。

Eq.\eqref{partfunc}から得られる古典的な運動方程式は以下です：
\begin{align} -\ddot x+\frac{\partial U}{\partial x}=0, \ \ \text{ただし}x(\beta)=x(0) \end{align}
ここで微分$\ddot x$は$\tau$による二階微分を表します。この運動方程式は、通常のポテンシャル$U$を逆さまにした系の運動に対応します（図2）。

ポテンシャル$U$を逆さまにしたグラフ

さらに境界条件より、時刻が$0$から$\tau$まで経過すると、元の位置に戻る運動を考えます。

この系に存在する古典解を考察します。
まず
\begin{align} x(\tau)=\pm a \end{align}
という解が存在します。これはずっと2つの山の頂上に留まる解です（図3）。

$x=-a$に留まる解

これは上記方程式の運動としては不安定なので、物理的ではないと思うかもしれませんが、元の系では安定な停留点の寄与を与えます。ポテンシャルがひっくり返っているのはあくまで計算上のテクニックであり、実際に物理量に寄与するか否かはこの系の運動の直感から類推してはいけないことに注意してください。

この系には更に、無限の過去にどちらかの山頂に存在し、無限の未来にもうひとつの山頂にたどり着く解が存在します（図4）。

無限の過去に$x=-a$に存在し、無限の未来で$x=a$に辿り着く解

この運動に対応する解は以下のように表されます：
\begin{align} x(\tau)=\pm a\tanh \left(\frac{\omega} {2}(\tau-\tau_0)\right) \end{align}
グラフにすると下図のようになります：

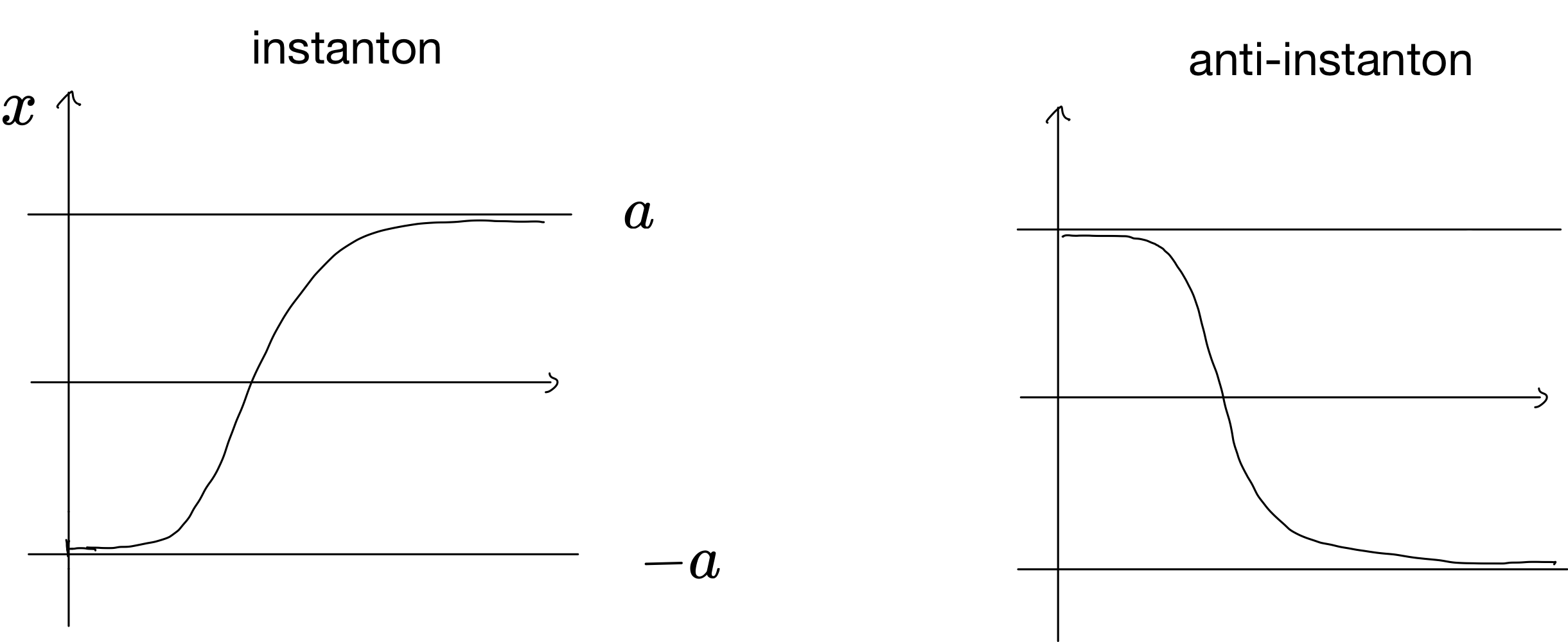インスタントン解（左図）と反インスタントン解（右図）

$-a$から$a$に辿り着く解をインスタントン、$a$から$-a$に辿り着く解を反インスタントンと言います。これらが運動方程式を満たすことはすぐに確かめられます。またこの解には$\tau_0$という任意パラメータが存在し、谷を通過する時刻に対応します。この任意パラメータの存在は時間並進不変性の反映です。

ただし、$x(\beta)=x(0)$より、片方の山から転がり落ちてもう一度同じ山の頂上に辿り着く解のみが分配関数に寄与します。インスタントンではそのような解を完全に記述することはできませんが、近似的にはインスタントンと反インスタントンをかけたものがそれに対応します。図6からわかるように、インスタントン・反インスタントンの時間方向の距離が十分離れているときに近似が良くなります。

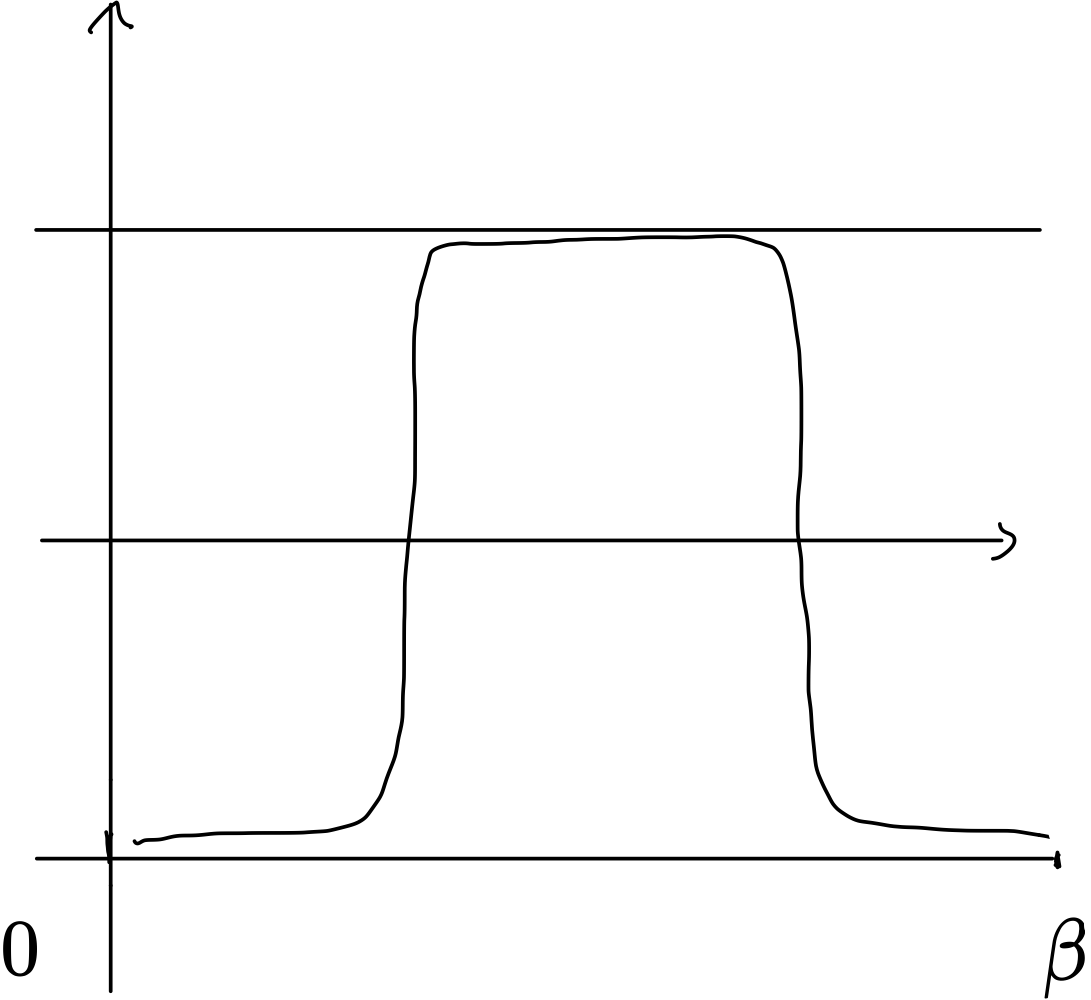インスタントンと反インスタントンの積

インスタントンペアの分配関数への寄与

ある山頂からもう一方の山頂に戻る解はすべて積分に寄与します。インスタントン・反インスタントンの組の数を$n$として、それらをすべて足しあげることを考えます。

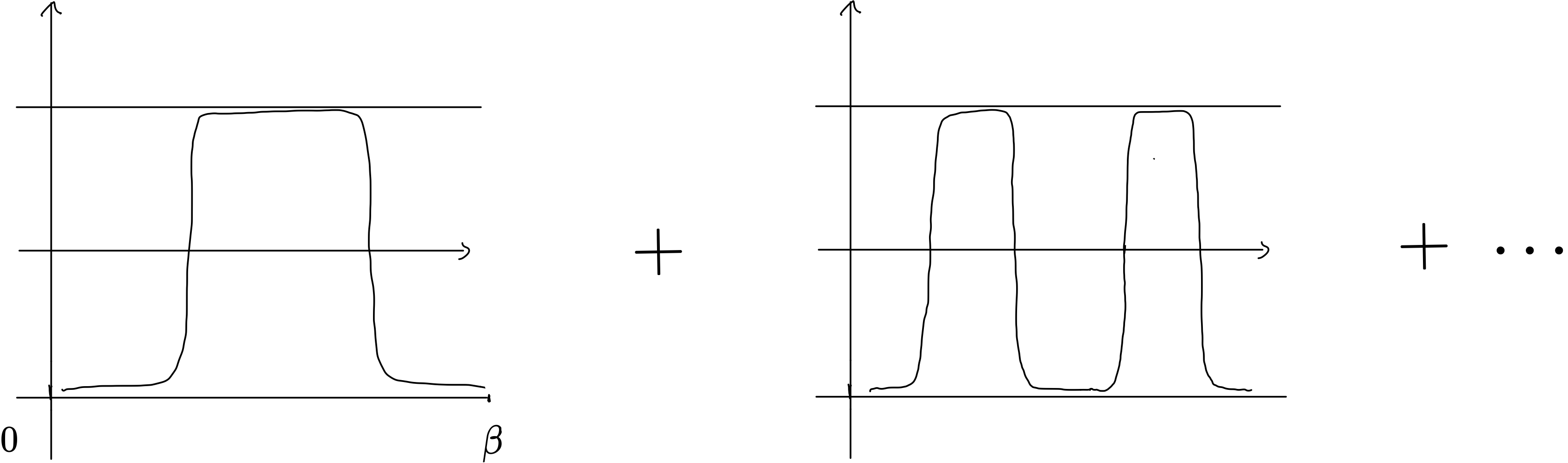インスタントンペアの分配関数の足し上げ

$n=1$の場合に関し、これがどのような積分の寄与をもたらすか考察します。$n=1$の解は図7の一番左のグラフです。まず、インスタントンと反インスタントの分配関数は同じなので、以下これらを$Z_1$と表記します。ここでインスタントンと反インスタントンが存在している領域を1および2とラベルします（図8）。経路積分および$\exp$の肩の虚時間の積分もこれらの領域に分割します。

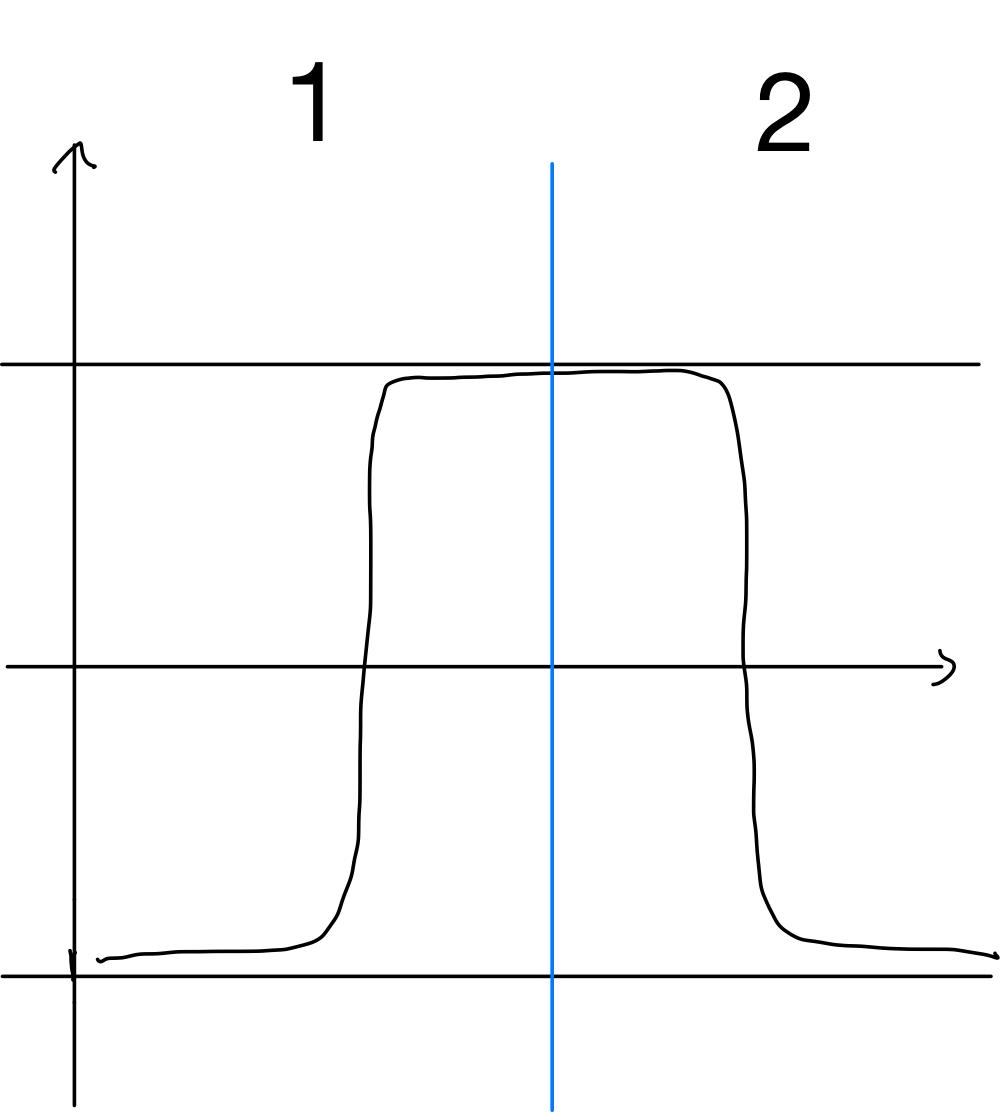領域を1と2にわける

$\beta\to \infty$では、$[0,\beta]$の範囲に比べ、（反）インスタントンが隣の山に移る時間間隔は非常に狭くなります。この状況では、全領域にインスタントンが1つ存在する状態の分配関数$Z_1$を、$x=a$に留まり続ける状態の分配関数$Z_0$で割ると、領域1にインスタントンが存在する分配関数を、領域1で$x=a$に留まる分配関数でわったものになります（図9）。

インスタントンの分配関数を$x=a$の停留点に留まる分配関数でわる

式で書けば
\begin{align} \frac{Z_1}{Z_0}=\frac{\displaystyle\int^{1+2}_{(1I)}{\cal D}x\exp\left[-\int^{1+2}d\tau L\right]}{\displaystyle\int^{1+2}_{(0)}{\cal D}x\exp\left[-\int^{1+2}d\tau L\right]} &= \frac{\displaystyle\int^{1}_{(1I)}{\cal D}x\exp\left[-\int^{1}d\tau L\right]\int^{2}_{(1I)}{\cal D}x\exp\left[-\int^{2}d\tau L\right]}{\displaystyle\int^{1}_{(0)}{\cal D}x\exp\left[-\int^{1}d\tau L\right]\int^{2}_{(0)}{\cal D}x\exp\left[-\int^{2}d\tau L\right]}\\ &\fallingdotseq \frac{\displaystyle\int^{1}_{(1I)}{\cal D}x\exp\left[-\int^{1}d\tau L\right]}{\displaystyle\int^{1}_{(0)}{\cal D}x\exp\left[-\int^{1}d\tau L\right]}\\ \end{align}
となります。ここで積分記号の上についている数字は領域を、下についているカッコつきの記号はインスタントンの数を表しています。同様に、全領域に反インスタントンが1つ存在する状態の分配関数$Z_1$を$Z_0$で割ると、領域2に反インスタントンが存在する分配関数を、領域2において$x=a$に留まる分配関数でわったものになります。

以上から、インスタントンペアが1組ある場合の分配関数$Z_{I+\bar I}$は
\begin{align} Z_{I+\bar I}/Z_0\sim (Z_1/Z_0)^2 \end{align}
になります（図10）。

インスタントンペアの分配関数の計算

この議論は一般の$n$コのインスタントンペアが存在する場合に容易に拡張できて
\begin{align} Z_{n(I+\bar I)}/Z_0\sim (Z_1/Z_0)^{2n} \end{align}
となります。

ただしこれらの関係には更に係数がつきます。なぜなら、例えば1組のインスタントンペアの場合、$Z_{I+\bar I}/Z_0$では1の領域にインスタントンおよび2の領域に反インスタントンが存在するという制限があるのに対し、$(Z_1/Z_0)^2$ではそのような制限がつかないからです。この制限は、分配関数を計算する際の（反）インスタントンの中心座標の積分の制限に対応します。制限つきの$n$コの（反）インスタントンの中心座標$\tau_1,\tau_2,\cdots,\tau_n$の積分は
\begin{align} \int_0^\beta d\tau_1 \int_0^{\tau_1} d\tau_2 \cdots \int_0^{\tau_{n-1}}d\tau_n \end{align}
です。これと制限なしの積分
\begin{align} \int_0^\beta d\tau_1 \int_0^\beta d\tau_2 \cdots \int_0^\beta d\tau_n \tag{1}\label{allint} \end{align}
との関係は
\begin{align} \int_0^\beta d\tau_1 \int_0^{\tau_1} d\tau_2 \cdots \int_0^{\tau_{n-1}}d\tau_n =\frac{1}{n!}\int_0^\beta d\tau_1 \int_0^\beta d\tau_2 \cdots \int_0^\beta d\tau_n \end{align}
です。なぜなら、Eq.\eqref{allint}の積分は一辺が$\beta$の$n$次元超立方体の体積ですが、これを$\tau_{i_1}>\tau_{i_2}>\cdots>\tau_{i_n}$を満たす領域に分解したとき、その領域の数は$i_1$から$i_n$に$1$から$n$を割り当てる通りの数$n!$であり、また各分割領域は同じ体積だからです。

以上より
\begin{align} Z_{n(I+\bar I)}=\frac{1}{(2n)!}A^{2n} Z_0, \ \ A:= \frac{\displaystyle\int_{(1I)}{\cal D}x\exp\left[ -\int_0^\beta d\tau L \right]}{\displaystyle\int_{(0)}{\cal D}x\exp\left[ -\int_0^\beta d\tau L \right]} \end{align}
を得ます。最終的に計算したい分配関数$Z(\beta)$は、ペアの個数に関して和をとり、かつ$x=a$又は$x=-a$から出発して元に戻る2通りの場合があることから
\begin{align} Z(\beta)=2Z_0\sum_{n=0}^\infty \frac{1}{(2n)!}A^{2n} =2Z_0\cosh A=Z_0(\exp(A)+\exp(-A)) \end{align}
となります。$x(\beta)=x(0)$の制限があるため、ペアで足し上げなければならないことに注意してください。

$W(\beta)=-\ln Z(\beta)$より、$E_0$は
\begin{align} E_0=-\lim_{\beta\to \infty}\frac{1}{\beta}W(\beta) =-\lim_{\beta\to \infty}\frac{1}{\beta}\ln Z_0 -\lim_{\beta\to \infty}\frac{1}{\beta}\ln (\exp(A)+\exp(-A)) \end{align}
$Z_0$は$x=a$に留まり続ける解の周りの量子ゆらぎを${\cal O}(\hbar^0)$まで取り入れた場合の分配関数であり、この運動は調和振動子であるから
\begin{align} Z_0=\sum_n \exp\left[-\omega\left(\frac{1}{2}+n\right)\beta\right] \end{align}
であり、基底状態のエネルギーは$\omega/2$になります。よって
\begin{align} E_0=\frac{\omega}{2}-\lim_{\beta\to \infty}\frac{1}{\beta}\ln (\exp(A)+\exp(-A)) \end{align}
を得ます。第２項がトンネル効果による基底状態のエネルギーのずれです。

改めて結果を公式の形で記しておきます。

今回はここまで。おしまい。${}_\blacksquare$

【次の記事】 インスタントンとトンネル効果 (3) : ゼロモードの除去、トンネル効果によるエネルギーシフト

Appendix: 統計系の分配関数の経路積分表示

統計力学的分配関数が経路積分表示を持つことを、以下簡単に紹介します。

分配関数は以下のように定義されます：

\begin{align} Z(\beta):={\rm tr}e^{-\beta \hat H} \end{align}
$\rm tr$は同じ状態ではさんで和を取ることを意味します。これは基底に依存しない量です。

基底として位置の固有状態$|q\rangle$をとります。すると
\begin{align} Z(\beta)=\int dq \langle q|e^{-\beta\hat H}| q\rangle \end{align}
となります。ここで$\beta=it$とすると、$e^{-\beta\hat H}$は虚時間における時間間隔$-i\beta$の時間発展演算子とみなすことができます。よって$Z(\beta)$は
\begin{align} Z(\beta)=\langle q,t=-i\beta|q,t=0\rangle \end{align}
という遷移振幅とみなすことができます。ただし初期状態と終状態は同じ$q$の状態であるという条件がつく（およびその状態で和をとる）ことに注意してください。つまり、虚時間を$\tau=it$で定義すると、$\tau=0$と$\tau=\beta$で周期境界条件が課されることになります。

こうするとあとは通常の経路積分表示の導出と同じ議論により、$Z(\beta)$を経路積分で表すことができます。虚時間を$N$等分し、時間発展演算子を$N$等分した微小時間間隔の時間発展演算子$\exp(-i\hat H\epsilon)$を導入します。ここで$\epsilon$は$t$の刻み幅であり虚数です。虚時間$\tau\in{\mathbb R}$（実数！）の刻み幅$\epsilon_\tau$との関係は$\epsilon_\tau=i\epsilon$です。各虚時刻において$q,p$の完全系を挟み、行列要素を計算すれば
\begin{align} Z(\beta)&=\prod_{i}\int dq_i \int \frac{dp_i}{2\pi} \exp \left( i\epsilon\sum_j^N \left\{ p_j(q_{j+1}-q_j)/\epsilon-H(q_j,p_j) \right\} \right)\\ &=\prod_{i}\int dq_i \int \frac{dp_i}{2\pi} \exp \left( \epsilon_\tau\sum_j^N \left\{ ip_j(q_{j+1}-q_j)/\epsilon_\tau-H(q_j,p_j) \right\} \right)\\ &\xrightarrow{\epsilon_\tau\to 0}\int {\cal D}q\int{\cal D}p \exp\left\{\int_0^\beta d\tau\left(ip\dot q-H(q,p)\right)\right\}\\ & \ \ \ \ \ \ (q,p: \text{periodic}, \ \ \dot q:=dq/d\tau) \end{align}
のように表せます。Hamiltonianを$\frac{1}{2}p^2+V(q)$と仮定し、$p$の積分を実行すれば、本文のEq.\eqref{partfunc}を得ます。詳しくは例えばKugoをご参照ください。

$\beta$は統計系では$1/T$（$T$は温度）であり、それゆえ$Z(\beta)$は温度を伴う理論の分配関数を表しています。大学で習うような物性系ではスピン系が扱われることが多く、基底として位置の固有状態をとることはあまりないかと思います。しかし上記の議論を用いると、例えば場の量子論にも温度を導入することができます。このようなformalismは松原武生等により議論され、虚時間形式とか松原形式と呼ばれます。${}_\blacksquare$