複素平面上の格子点に零点をもつ関数

三角関数の無限積を拡張した以下のような関数について考えました。
$$ f(z) = z \prod_{(n,m) \neq (0,0)} \left(1-\frac{z}{n + i m}\right) $$
追記：間違いを訂正しました

背景

複素関数は２次元の静電場を表すことを知り、いろいろな電荷分布における電場を考えました。位置$a$にある電荷$Q_a$の作る電場は
$$ w = (Q_a/2\pi) \ln (z-a) $$
という関数で表され、複数の電荷が作る電場は

\begin{eqnarray} w &=& (Q_a/2\pi) \ln (z-a) + (Q_b/2\pi) \ln (z-b) + (Q_c/2\pi) \ln (z-c) + ~.. \\ &=& (1/2\pi) \ln((z-a)^{Q_a}(z-b)^{Q_b}(z-c)^{Q_c} ~ ..) \end{eqnarray}
と表せます。ここで$z=x+ iy$は空間座標を表し、$w=\phi+ i\nu$ は電位と等電位線にそった位置を表します。これから電気力線や等電位線を求めるためには、これの逆関数を求め、$z=f^{-1}(w)$の形にする必要があります。

直線に並んだ電荷の列が作る電場

対数の中を$g(z)$とすると$2 \pi w =\ln g(z)$ という形になります。電荷を１とし実軸状に間隔１で並べたものを考えると
$$ g(z) = z(z-1)(z+1)(z-2)(z+2)(z-3)(z+3) ~ .. $$
になります。ここで$\ln g(z) + C$のように定数項を足すことは、電位の基準をずらすことと同じです。電位の基準はどこにとってもいいので、$g(z)$に好きな定数を掛けることができます。なので
\begin{eqnarray} g(z) &=& \pi z(1-z)(1+z)(1-z/2)(1+z/2)(1-z/3)(1+z/3) ~ .. \\ &=& \sin(\pi z) \end{eqnarray}
を考えます。
$$ 2 \pi w = \ln \sin(\pi z) $$
より
$$ z = \frac{\arcsin (e^{2 \pi w})}{\pi} $$
これを描画すると以下のようになります。
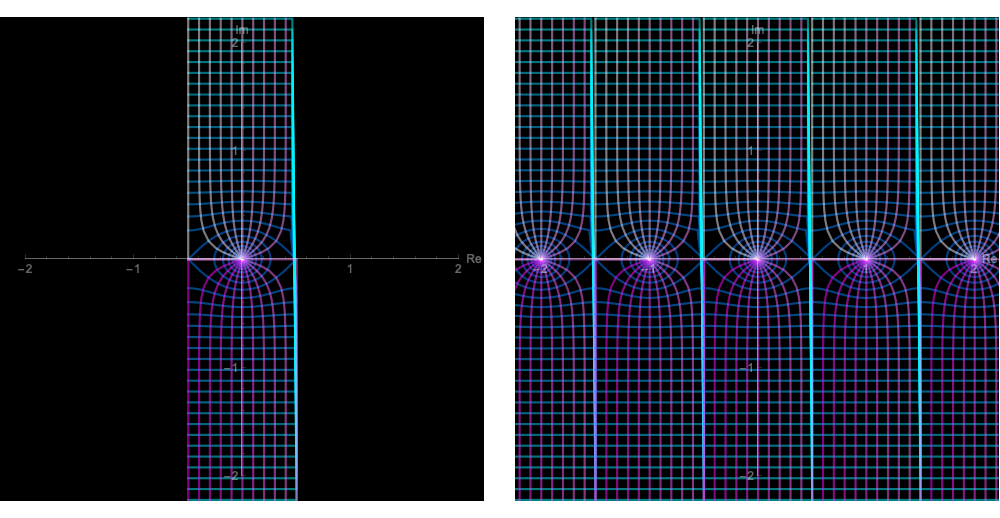並んだ電荷が作る電場
複素関数が多価のときもプログラムの関数は一つの主値を返すよう作られているので、別の分岐の関数を手動で求めて足さないといけません。$\arcsin(x)$は実軸に$\pi$ずらすだけなので簡単です。

正と負が交互に並んだ電荷の列が作る電場

$$ g(z) = z\frac{z^2-4}{z^2-1}\frac{z^2-16}{z^2-9}\frac{z^2-36}{z^2-25} ~ .. $$
定数倍はノーカンなので
$$ g(z) = z\frac{1-z^2/4}{1-z^2}\frac{1-z^2/16}{1-z^2/9}\frac{1-z^2/36}{1-z^2/25} ~ .. = \frac{\sin(\pi z /2)}{\cos (\pi z /2)} = \tan (\pi z /2) $$
逆関数は
$$ z = \frac{2 \arctan (e^{2 \pi w})}{\pi} $$
正負が交互に並んだ場合

本題

ここまでくると、格子状にならんだ電荷が作る電場を知りたくなります。ここで冒頭の式がでてくるわけです。
$$ f(z) = z \prod_{(n,m) \neq (0,0)} \left(1-\frac{z}{n + i m}\right) $$
まず$n$についての掛け算を先にします。下図の青の方向です。
格子
まず以下の式
\begin{eqnarray} \frac{\sin \pi (a -b)}{\sin \pi a} &=& \frac{(a-b) (1 -(a-b))(1+(a-b))(1 -(a-b)/2)(1 -(a-b)/2)~..}{a(1-a)(1+a)(1-a/2)(1+a/2)~..} \\ &=&\left(1 - \frac{b}{a}\right) \left(1 - \frac{b}{a-1}\right) \left(1 - \frac{b}{a+1}\right) \left(1 - \frac{b}{a-2}\right) \left(1 - \frac{b}{a+2}\right) ~.. \tag{1} \label{eq1} \end{eqnarray}に$a=i m,b=z$を代入して
$$ \frac{\sin \pi (i m -z)}{\sin \pi i m} = \left(1 - \frac{z}{im}\right) \left(1 - \frac{z}{im-1}\right) \left(1 - \frac{z}{im+1}\right) \left(1 - \frac{z}{im-2}\right) \left(1 - \frac{z}{im+2}\right) ~.. $$
を得ます。$m=0$ のとき
$$ \sin \pi z = \pi z(1-z)(1+z)(1-z/2)(1+z/2)(1-z/3)(1+z/3) ~.. $$
であることをふまえ$m$についての積をとると
$$ f(x) = \frac{\sin \pi z}{\pi} \prod_{m\neq 0} \frac{\sin \pi (im -z)}{\sin \pi im} $$
${\sin i z = i \sinh z}$と加法定理を使うと
$$ \frac{\sin \pi (im -z)}{\sin \pi im} = \cos \pi z - i \coth \pi m ~ \sin \pi z $$
$m$にマイナスをかけると複素共役になるので
\begin{eqnarray} f(x) &=& \frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} (\cos^2 \pi z+ \coth^2 \pi m ~ \sin^2 \pi z) \\ &=& \frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) \end{eqnarray}
となります。今度は$m$についての掛け算を先にしてみます。\eqref{eq1}に$a=i n,b=z i$を代入し
$$ \frac{\sin \pi (i n - i z)}{\sin \pi n i} = \left(1 - \frac{z}{n }\right) \left(1 - \frac{z}{n-i}\right) \left(1 - \frac{z}{n+i}\right) \left(1 - \frac{z}{n-2i}\right) \left(1 - \frac{z}{n+2i}\right) ~.. $$
これから同様の計算をし
\begin{eqnarray} f(z) &=& \frac{\sinh \pi z}{\pi} \prod_{n=1}^{\infty} (\cosh^2 \pi z- \coth^2 \pi n ~ \sinh ^2 \pi z) \\ &=& \frac{\sinh \pi z}{\pi} \prod_{n=1}^{\infty} \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi n}\right) \end{eqnarray}

おかしい

この２つの式はかける順番を変えただけで同じはずですが、これらの関数には縦横の"向き"が違っています。そもそも縦横対称の格子なのに向きが生じる時点でおかしいです。実際
$$ f_1(z) = \frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) $$
$$ f_2(z) = \frac{\sinh \pi z}{\pi} \prod_{n=1}^{\infty} \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi n}\right) $$
とすると$f_1(z)$は$ \mathrm{Im}(z) \to \infty $で発散して、$\mathrm{Re}(z) \to \infty$ では発散しません。また$f_1(i z) = i f_2(z)$となり向きが90度回転します。ある程度で打ち切った部分積をMathematicaの描画関数で描かせると以下のようになります。
$\frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right)$
"正解"を知るため$9 \times 9$の格子についての積を描画すると以下のようになります。
$9 \times 9$の格子による$f(z)$

似たようなケースは例えば以下の級数でも起こります。
$1 - 1/2 + 1/3 - 1/4 + 1/5 - ~.. = \ln 2$
これは以下のように足し方を変えると違う値になります。
$(1 + 1/3) - 1/2 + (1/5 + 1/7) - 1/4 + (1/9 + 1/11) - 1/6 + ~.. = (3/2) \ln 2$
今回もx方向とy方向で均等に掛けないために違いが生まれたようです。

均等な掛け方を考える

方法1

なるべく均等にかけるため下図のように4つをまとめて掛けたらどうなるでしょうか
4つづつまとめる
$$ \left(1 \pm \frac{x}{n \pm i m}\right) $$
の形の項をすべてかけると
$$ \left(1 - \frac{x^2}{(n + i m)^2}\right) \left(1 - \frac{x^2}{(n - i m)^2}\right) $$
という形になります。ここで
\begin{eqnarray} \frac{\cos 2\pi b - \cos2 \pi a}{1 - \cos2 \pi a} &=& \frac{\sin((a+b)\pi)}{\sin (a\pi)}\frac{\sin((a-b)\pi)}{\sin (a\pi)}\\ &=& \left(\left(1 + \frac{b}{a}\right) \left(1 + \frac{b}{a-1}\right) \left(1 + \frac{b}{a+1}\right) \left(1 + \frac{b}{a-2}\right) \left(1 + \frac{b}{a+2}\right) ~ ..\right) \cdot \\ && \left(\left(1 - \frac{b}{a}\right) \left(1 - \frac{b}{a-1}\right) \left(1 - \frac{b}{a+1}\right) \left(1 - \frac{b}{a-2}\right) \left(1 - \frac{b}{a+2}\right) ~ ..\right) \\ &=& \left(1 - \frac{b^2}{a^2}\right) \left(1 - \frac{b^2}{(a-1)^2}\right) \left(1 - \frac{b^2}{(a+1)^2}\right) \left(1 - \frac{b^2}{(a-2)^2}\right) \left(1 - \frac{b^2}{(a+2)^2}\right) ~ .. \end{eqnarray}
これに$a=im,b = z$をいれると
\begin{eqnarray} \frac{\cos 2\pi z - \cos 2\pi i m}{1 - \cos 2\pi i m} &=& \left(1 + \frac{z^2}{m^2}\right) \left(1 - \frac{z^2}{(1-im)^2}\right) \left(1 - \frac{z^2}{(1+im)^2}\right) \left(1 - \frac{z^2}{(2-im)^2}\right) \left(1 - \frac{z^2}{(2+im)^2}\right) ~ .. \end{eqnarray}
また
\begin{eqnarray} \frac{\cos 2\pi z - \cos 2\pi i m}{1 - \cos 2\pi i m} &=& \frac{\cos 2\pi z - \cosh 2\pi m}{1 - \cosh 2\pi m} = 1 - \frac{1 - \cos \pi z}{1 - \cosh \pi m} \\ &=&1 + \frac{\sin^2 (\pi z)}{\sinh^2 (\pi m)} \end{eqnarray}
$m=0$のときは$\sin \pi z/\pi$をかければよく
\begin{eqnarray} f(x) &=& \frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 (\pi z)}{\sinh^2 (\pi m)}\right) \end{eqnarray}
前と同じ形になりました。はじめ計算ミスをしていて違うことをしているつもりでしたが、結局同じことをしていました。失礼しました。

方法2

均等に二重カウントする
上図の同じ色のラインをまとめてかけていくと、すべての点で二重カウントされることがわかります。この計算は結果的にさきほどの$f_1(z),f_2(z)$の積になるので
$$ f(x) ^2 = \frac{\sin \pi z}{\pi} \frac{\sinh \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi m}\right) $$
よって
$$ f(x) = \sqrt{\frac{\sin \pi z}{\pi} \frac{\sinh \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi m}\right)} $$
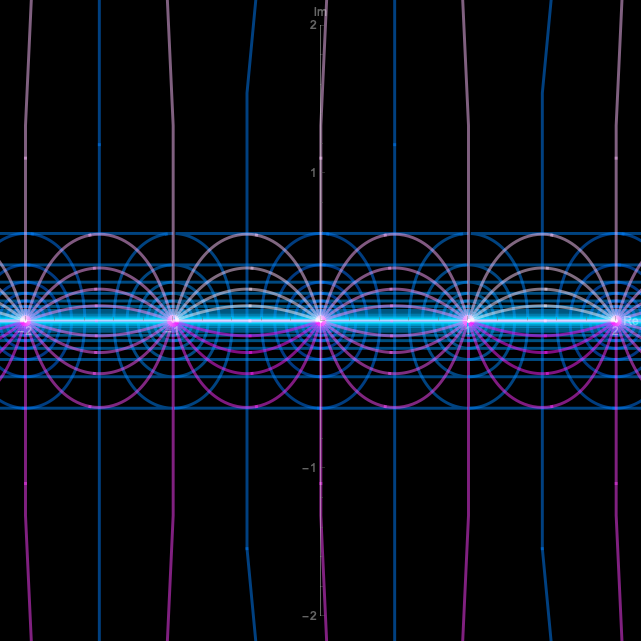
これを描画すると以下のようになりました。
$\sqrt{\frac{\sin \pi z}{\pi} \frac{\sinh \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi m}\right)}$
ルートを取ったので正負が逆になっているところがありますが、正しく分岐をとれば$9 \times 9$の格子のものと十分に一致することがわかりました。しかしこの関数は周期的な模様はあるのですが、x方向、y方向ともに完全な周期性はありません。

まとめ

$$ f(z) = z \prod_{(n,m) \neq (0,0)} \left(1-\frac{z}{n + i m}\right) $$
はかける順番により以下のような違う関数に近づく

• はじめに$n$についてかける場合
  $$ f_1(z) = \frac{\sin \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) $$
• はじめにmについてかける場合
  $$ f_2(z) = \frac{\sinh \pi z}{\pi} \prod_{n=1}^{\infty} \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi n}\right) $$
• 均等にかける場合
  \begin{eqnarray} f_3(z) &=& \sqrt{f_1(x)f_2(x)} \end{eqnarray}
  これらどの関数もxy両方向の完全な周期性はない

物理として解く

周期的な電位分布$\phi(x,y)$は以下のようにフーリエ級数展開できます。
$$ \phi(x,y) = \sum_{n,m=-\infty}^{\infty}c_{n,m} e^{2 \pi i (n x + m y)} $$
ここで
$$ c_{n,m} = \int_{-1/2}^{1/2} dx \int_{-1/2}^{1/2} dy ~ \phi(x,y) e^{- 2 \pi i (n x + m y)} $$
ここで$x:(-1/2,1/2)$$y:(-1/2,1/2)$の領域を基本領域としました。これを用いてポアソンの方程式$-\nabla^2 \phi = \rho(x)$を解きます。ところで複素関数で電場を表す場合、$\phi + i \nu = f(x+iy)$となりますが、
コーシー・リーマンの方程式$\phi_x = \nu_y,\phi_y,-\nu_x$より$\nabla^2\phi=0$が成り立ちます。これは正則な点では成立しますが、対数分岐点で右辺が有限になります。実はガウスの定理とコーシーの積分定理は関係していて領域$S$の境界を$\partial S$とし
$$ \int_S \nabla^2 \phi ~ dS = \int_{\partial S} f'(z) dz $$
です。なので$\nabla^2 \phi$が有限な点に$1/z$の積分にあたる対数分岐点があるわけです。
同じことを言ってるのがポアソンの方程式で、電荷がある点だけ$\nabla^2 \phi $が有限になります。これを使うと
\begin{eqnarray} \nabla^2 \phi(x,y) &=& -\rho(x,y) &=& - 4 \pi^2 \sum_{n,m}(n^2+m^2)c_{n,m} e^{2 \pi i (n x + m y)} \end{eqnarray}
となります。後に考えたことですが、$f$が全面で正則だと左辺が0になり、これを満たすのは$c_{0,0}$以外$0$となるときなので、楕円関数のリウヴィルの第一定理と同じことだと思います。
この式に$e^{-2 \pi i (Nx+My)}$をかけ$x:(-1/2,1/2)$$y:(-1/2,1/2)$の領域で積分します。
\begin{eqnarray} \int_{-1/2}^{1/2} dx \int_{-1/2}^{1/2} dy ~\rho(x,y) e^{-2 i \pi (Nx+My)} &=& 4 \pi^2 (N^2+M^2)c_{N,M} \end{eqnarray}
$\rho(x,y)=4 \pi^2 \delta(x,y)$とします。すると
$$ c_{n,m} =\frac{1}{(n^2+m^2)} $$
$c_{0,0}=\infty$となりますが、定数項なので一次元のときと同じように、電位の基準を調節すれば取り除けます。よって
\begin{eqnarray} \phi(x,y) &=& \sum_{(n,m)\neq(0,0)} \frac{e^{2 \pi i (n x + m y)}}{n^2+m^2} \\ &=& \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{2}{n^2+m^2} (\cos(2 \pi (nx+my)) \cos(2 \pi (nx-my))) \\ &+& \sum_{n=1}^{\infty}\frac{2}{n^2} \cos(2 n \pi x) +\sum_{n=1}^{\infty}\frac{2}{n^2} \cos(2 n \pi y ) \end{eqnarray}
部分和をプロットしてみると以下のようになります。
$\phi(x,y)$
これに対応する複素関数はあるのかということなのですが、$ e^{2 \pi i (n x + m y)}$ の$n x + m y$の部分が$dxdy$の正方形を一般には歪めるので正則な操作になりません。ただ和をとるときに$(n,m)$の組をうまくとればいけそうな気もします。

楕円関数

いろいろ関連分野について調べたところ、楕円関数がこれに関係あることがわかりました。複素平面で格子の周期性をもつ関数を楕円関数とよぶそうです。（これのことだったのか！！！）
今回得た２つの関数はテータ関数$\theta_1$ とヴァイエルシュトラスの$\sigma$函数で表せることがわかりました。
まずテータ関数$\theta_1(v,\tau)$を
$$ \theta_1(v,\tau) = \frac{1}{i} \sum_{n=-\infty}^{\infty} (-1)^n q^{(n+1/2)^2}z^{n+1/2} ~~ (q=e^{\pi i \tau },z = e^{2 \pi i v }) $$
とします。すると
\begin{eqnarray} \frac{\sin \pi z}{\pi} \prod_{k=1}^{\infty} \left(1+\left(\frac{\sin \pi z}{\sinh \pi k}\right)^2\right) = e^{-\pi/3}\cdot \theta_1(z, i) \end{eqnarray}
となるようです。そして
$$ g_2=\left(\frac{\Gamma(1/4)^4}{4\pi}\right)^2,g_3=0 $$
としたときのヴァイエルシュトラスの$\sigma$函数で
\begin{eqnarray} \sqrt{\frac{\sin \pi z}{\pi} \frac{\sinh \pi z}{\pi} \prod_{m=1}^{\infty} \left(1+ \frac{\sin^2 \pi z}{\sinh^2 \pi m}\right) \left(1 - \frac{\sinh^2 \pi z}{\sinh^2 \pi m}\right)} = \sigma(z) \end{eqnarray}
となります。そして
$$ e^{-\pi/3}\cdot \theta_1(z, i) = \sigma(z) e^{\pi z^2/2} $$
だそうです。ここらへんは後に勉強しようと思います。

数学に"訂正"された！

格子電荷の電場に対応する正解の複素関数はヴァイエルシュトラスの$\sigma$函数のようです。これの逆関数は求まらなそうなので、Mathematicaの等高線を書かせる関数で$\ln \sigma(z)$の実数部分の等高線を描画します。
$\textrm{Re}(\ln \sigma(z)$)
すきまに負電荷が挟まってる！！！
現実の結晶とかはこうなっているので、数学のほうが現実に詳しいってことでしょうか？驚きです。

ありがとうございました。