組合せ論と母関数２：自然数の分割

はじめに

prevの結果を使います。

自然数の分割

$a,b,c,..$の代わりに$q,q^2,q^3,..$を使います。すると積は指数の和になり、自然数の分割に関係した式になります。

べき乗和

べき乗和は以下のようになります。
\begin{eqnarray} p_1&=&q+q^2+q^3+~.. = \frac{q}{1-q}\\ p_2&=&q^2+q^4+q^6+~.. = \frac{q^2}{1-q^2}\\ p_3&=&q^3+q^6+q^9+~.. = \frac{q^3}{1-q^3}\\ ~.. \end{eqnarray}
べき乗和の母関数より
\begin{eqnarray} P &=& \frac{qz}{1-qz} + \frac{q^2z}{1-q^2z} + \frac{q^3z}{1-q^3z} +~.. \\ &=& \frac{qz}{1-q} + \frac{q^2z^2}{1-q^2} + \frac{q^3z^3}{1-q^3} + \end{eqnarray}

基本対称式

k次の基本対称式は異なるk個の文字からなる項の和です。
\begin{eqnarray} s_1&=&q+q^2+q^3+q^4+q^5+q^6+q^7+~.. \\ s_2&=&q^3+q^4+2q^5+2q^6+3q^7+3q^8+4q^9+4q^{10}+~.. \\ s_3&=&q^6+q^7+2q^8+3q^9+4q^{10}+5q^{11}+7q^{12}+8q^{13}~.. \\ ~.. \end{eqnarray}
$s_k$は$q,q^2,q^3..$のうち$k$個の異なる文字からなる項の総和ですが、$q$の指数は異なる自然数の和になり、この和が$j$になる組み合わせの数が$q^j$の係数となります。$j$を$k$個の異なる自然数に分割する方法の数を$q_k(j)$とすると、以下のように表せます。
\begin{eqnarray} s_k&=&\sum_{j=1}q_k(j) q^j \end{eqnarray}
ちなみにk個の異なる自然数に分割できる最小の自然数は$k(k+1)/2$なので、$j< k(k+1)/2$のとき、$q_k(j)=0$です。つまり級数は$q^{k(k+1)/2}$から始まります。ニュートンの恒等式より
\begin{eqnarray} s_1 &=& \frac{q}{1-q}\\ 2s_2 &=& \frac{qs_1}{1-q} - \frac{q^2}{1-q^2}\\ 3s_3 &=& \frac{qs_2}{1-q} - \frac{q^2s_1}{1-q^2} + \frac{q^3}{1-q^3}\\ .. \end{eqnarray}
これより
\begin{eqnarray} s_1 &=& \frac{q}{1-q}\\ s_2 &=& \frac{q^3}{(1-q)(1-q^2)}\\ s_3 &=& \frac{q^6}{(1-q)(1-q^2)(1-q^3)}\\ ~.. \end{eqnarray}
これから以下のような予想ができます。
\begin{eqnarray} s_1 &=& p_1\\ s_2 &=& p_1 p_2\\ s_3 &=& p_1 p_2 p_3\\ ~.. \end{eqnarray}
別の方法でもこの結果を得ることができます。
\begin{eqnarray} R(z) &=& (1+qz)(1+q^2z)(1+q^3z)~..\\ &=&1 + s_1 z + s_2 z^2 +~.. \\ &=&(1+qz)R(qz) \end{eqnarray}
これから係数比較により
\begin{eqnarray}  & 1 & ~~~ & z & ~~~ & z^2 & ~~~ & z^3 & ~~~ & z^4 & & .. \\   & 1 & & s_1 & & s_2 & & s_3 & & s_4 & & .. \\ =~& 1 &  & q s_1 & & q^2 s_2 & & q^3 s_3 & & q^4 s_4& & ..\\   &   &  & q &   & q^2 s_1 & & q^3 s_2 & & q^4 s_3 & & .. \\  \end{eqnarray}
よって
\begin{eqnarray}  s_1 &=& q (s_1+1) \\ s_2 &=& q^2 (s_2+s_1) \\ s_3 &=& q^3 (s_3+s_2) \\ .. \end{eqnarray}
これより
\begin{eqnarray} s_1 &=& \frac{q}{1-q}\\ s_2 &=& \frac{q^3}{(1-q)(1-q^2)}\\ s_3 &=& \frac{q^6}{(1-q)(1-q^2)(1-q^3)}\\ ~.. \end{eqnarray}
一般に
$$ s_m = \frac{q^{m(m+1)/2}}{(1-q)(1-q^2)~..(1-q^m)}　=\sum_{j=1}^{\infty}q_m(j) q^j $$
となります。よって
\begin{eqnarray} R&=&(1+qz)(1+q^2z)(1+q^3z)~..\\ &=&1 + \frac{qz}{1-q} + \frac{q^3z^2}{(1-q)(1-q^2)} + \frac{q^6z^3}{(1-q)(1-q^2)(1-q^3)} +~.. \end{eqnarray}

自然数の分割

$n$を$m$個の異なる自然数に分割する方法の数を$q_m(n)$とします。いまの結果から
$$ s_m = \frac{q^{m(m+1)/2}}{(1-q)(1-q^2)..(1-q^m)} = \sum_{k=1}q_m(k)q^k $$
両辺に$q^{-m}$をかけると
$$ \frac{q^{m(m-1)/2}}{(1-q)(1-q^2)..(1-q^m)} = \sum_{k=1}q_m(k)q^{k-m} $$
$k< m(m+1)/2$のとき$q_m(k)=0$なので$q$の指数がマイナスの項などは生じません。後者から前者を引くと
\begin{eqnarray}  &&\frac{q^{m(m-1)/2}-q^{m(m+1)/2}}{(1-q)(1-q^2)..(1-q^m)} \\ &=& \frac{q^{m(m-1)/2}}{(1-q)(1-q^2)..(1-q^{m-1})} = \sum_{k=1}q_{m-1}(k)q^k \end{eqnarray}
これから$q^k$の係数を比較して以下の関係式を得ます。

ヤング図形による図解

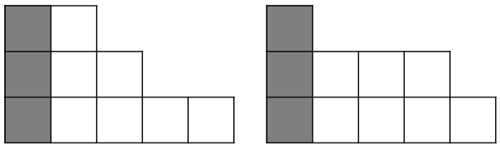左：1を含まない分割,　 右：1を含む分割
自然数の分割はヤング図形により表すことができます。例えば図1はそれぞれ$2+3+5$ ,$1+4+5$という分割を表します。$q_m(n)$個のヤング図形はすべて、１を含む分割か、１を含まない分割のいずれかに分類できます。まず1を含まない場合（左図）、色のついたブロックを消すと、縦の段数はmのまま、ブロック数は$n-m$になります。このとき残ったヤング図形は$q_m(n-m)$に対応します。1を含む場合、同様に色のついたブロックを消すと、ブロック数は同じく$n-m$になりますが、縦の段数が一つ減るので$q_{m-1}(n-m)$に対応するヤング図形になります。よって$q_m(n)= q_m(n-m) + q_{m-1}(n-m)$が成り立ちます。

異なるルールの分割数との関係

$j$を$m$個の異なる自然数に分割する数を$p_m(j)$として
\begin{eqnarray} \frac{q^{m(m+1)/2}}{(1-q)(1-q^2)~..(1-q^m)}　= \sum_{j=1}^{\infty}q_m(j) q^j \end{eqnarray}
ですが
\begin{eqnarray} \frac{1}{(1-q)(1-q^2)~..(1-q^m)} \end{eqnarray}
は完全斉次式の母関数の形をしています。これは重複を許した組み合わせの項からなるので、重複を許した自然数の分割に関係します。用語の使用に関してですが、重複を許すルールをデフォルトにし、許さない場合は「異なる」をつけることにします。$j$を$1,2,~..,m$によって分割する数を$p_{\leq m}(j)$（独自の記法）とすると
\begin{eqnarray} \frac{1}{(1-q)(1-q^2)~..(1-q^m)} = \sum_{j=1}^{\infty}p_{\leq m}(j) q^j \end{eqnarray}
よって

ヤング図形による図解

左：$q_m(n)$, 右：$p_{\leq m}(n-m(m+1)/2) $
$m$個の異なる自然数からなる分割において、分割を$(a_1,a_2,..,a_m)$のように表し、昇順にすると隣合う数字は必ず１以上の差があります。このため$b_k\ge0$となる$(b_1,b_2,..b_m)$を使って$(a_1,a_2,..,a_m)=(1,2,..,m)+(b_1,b_2,..,b_m)$と表せます。図２の左図のグレーの部分が$(1,2,..,m)$という分割に対応します。グレーの部分のブロック数は$m(m+1)/2$なのでこれを引いた$(b_1,b_2,..,b_m)$は$n-m(m+1)/2$の分割に対応します。$(b_1,b_2,..,b_m)$は図2の右図のように並べることができ、これは$n-m(m+1)/2$を1からmまでの自然数で分割する方法に等しくなります。

完全斉次式

\begin{eqnarray} h_1&=&q+q^2+q^3+q^4+q^5+q^6+q^7+~.. \\ h_2&=&q^2+q^3+2q^4+2q^5+3q^6+3q^7+4q^8+4q^9+~.. \\ h_3&=&q^3+q^4+2q^5+3q^6+4q^7+5q^8+7q^9+8q^{10}~.. \\ ~.. \end{eqnarray}
$j$を$k$個の自然数に分割する方法の数を$p_k(j)$とすると、以下のように表せます。
\begin{eqnarray} h_k&=&\sum_{j=1}^{\infty}p_k(j) q^j \end{eqnarray}

\begin{eqnarray} V(z)&=&\frac{1}{(1-qz)(1-q^2z)(1-q^3z)~..}\\ &=&1 + h_1 z + h_2 z^2 +~..\\ &=& (1-qz)V(qz) \end{eqnarray}
から係数比較より
\begin{eqnarray}  h_1 &=& q(h_1+1) \\ h_2 &=& q (h_2 q+h_1) \\ h_3 &=& q (h_3 q^2+h_2) \\ .. \end{eqnarray}
よって
\begin{eqnarray}  h_1 &=& \frac{q}{1-q} \\ h_2 &=& \frac{q^2}{(1-q)(1-q^2)} \\ h_3 &=& \frac{q^3}{(1-q)(1-q^2)(1-q^3)} \\ .. \end{eqnarray}
一般に
$$ h_m = \frac{q^m}{(1-q)(1-q^2)~..(1-q^m)}=\sum_{j=1}^{\infty}p_m(j) q^j $$
となります。よって
\begin{eqnarray} V&=&\frac{1}{(1-qz)(1-q^2z)(1-q^3z)~..}\\ &=&1 + \frac{qz}{1-q} + \frac{q^2z^2}{(1-q)(1-q^2)} + \frac{q^3z^3}{(1-q)(1-q^2)(1-q^3)} +~.. \end{eqnarray}

異なるルールの分割数との関係

基本対称式の結果と比較すると
\begin{eqnarray}  s_1 &=& h_1 \\ s_2 &=& q h_2 \\ s_3 &=& q^3 h_3 \\ s_4 &=& q^6 h_4 \\ .. \end{eqnarray}
一般に
\begin{eqnarray}  s_m &=& q^{m(m-1)/2} h_m \end{eqnarray}
これから以下の関係を得ます。

ヤング図形による図解

左：$q_m(n)$, 右：$p_{m}(n-m(m-1)/2)$
$(a_1,a_2,..,a_m)=(0,1,..,m-1)+(b_1,b_2,..,b_m)$のように分割すると$ (b_1,b_2,..b_m)$は$b_k\ge1$となり、ブロック数は$n-m(m-1)/2$となります。$(b_1,b_2,..b_m)$の数は$n-m(m-1)/2$をm個の自然数で分割する方法に等しくなります。

分割数の再帰式

いまの式を公式１
\begin{eqnarray} q_m(n+m)= q_m(n) + q_{m-1}(n) \end{eqnarray}
に代入すると
\begin{eqnarray} p_m(n-m(m-3)/2)= p_m(n-m(m-1)/2) + p_{m-1}(n-(m-1)(m-2)/2) \end{eqnarray}
変数を置き換えると以下の式を得ます。

ヤング図形による図解

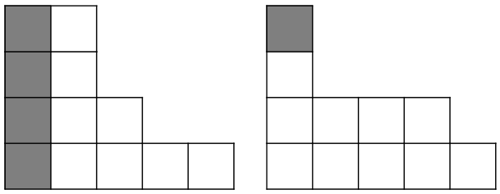左：1を含まない分割,　 右：1を含む分割
nをm個に分割する方法は、1を含む分割とそうでない分割に分けれます。１を含まない分割から、グレーの部分を引くと、n-mをm個に分割するヤング図形になるので、$p_m(n-m)$に対応します。１を含む分割は右図のヤング図形になります。これからグレー部分を引くと$p_m(n-1)$に対応するヤング図形になります。このため
$p_m(n)= p_m(n-m) + p_{m-1}(n-1)$
となります。

問題によってヤング図形の操作が違う理由

同じ議論が$q_m(n)$にも使えるじゃないかと思われるかもしれませんが、$q_m(n)$では、１が一回しか使えないので、その１を引くと、2以上の異なる自然数からなる分割となり、分割のルールが変わってしまいます。逆に$p_m(n)$の１を含む場合からnを引くと、１の個数によって異なる個数への分割になってしまいます。同じルールの分割数どうしの関係を得たいので、問題によってヤング図形の操作が違うのです。

z=1のとき

$z=1$とすると$m$個に分割するという制限がなくなります。nを異なる自然数に分割する数を$q(n)$,nを自然数に分割する数を$p(n)$とすると
\begin{eqnarray} R &=& (1+q)(1+q^2)(1+q^3)~.. &=& 1 + \sum_{n=1}^{\infty} q(n) q^n \\ V &=& \frac{1}{(1-q)(1-q^2)(1-q^3)~..} &=& 1 + \sum_{n=1}^{\infty} p(n) q^n \end{eqnarray}
となります。

オイラーの分割恒等式

\begin{eqnarray} (1+q)(1+q^2)(1+q^3)~.. &=& \frac{(1-q^2)(1-q^4)(1-q^6)(1-q^8)..}{(1-q)(1-q^2)(1-q^3)(1-q^4)..}\\ &=& \frac{1}{(1-q)(1-q^3)(1-q^5)..} \end{eqnarray}
なのでnを異なる自然数に分割する方法の数を$q(n)$、nを奇数によって分割する数を$p_{odd}(n)$とすると

組み合わせ論的考察

全ての自然数は$(2n-1)*2^m$という形で表せます。これを表にすると
\begin{eqnarray} &&1,2,4,..\\ &&3,6,12,..\\ &&5,10,20,..\\ &&7,14,28,.. \end{eqnarray}
二進数表記を考えれば、全ての自然数は先頭の奇数2n-1と末尾の連続する０の数mを用いた、(n,m)という組に一意に対応することが分かると思います。
\begin{eqnarray} 1&\cdot&(1,10,100,1000,..)\\ 11&\cdot&(1,10,100,1000,..)\\ 101&\cdot&(1,10,100,1000,..)\\ ..&& \end{eqnarray}
全ての自然数はこの表のどれかに対応するので、異なる自然数への分解はこの表のいくつかを埋めたものに対応します。各行の埋まりかたは自然数$a,b,c,..$の二進数表示と対応させることができ、
\begin{eqnarray} 1&\cdot&a\\ 11&\cdot&b\\ 101&\cdot&c\\ ..&& \end{eqnarray}
というように表せます。これは奇数を用いた分割を表します。例えば$13=3+4+6$は
\begin{eqnarray} 1&\cdot&(0,0,1)\\ 11&\cdot&(1,1) \end{eqnarray}
なので$1\cdot100 + 11\cdot11 = 1\cdot4+3\cdot3 = 1+1+1+1+3+3+3$に対応します。

二進数表記の一意性

$a,b,c~..$として$q,q^2,q^4,q^8..$を考えます。
\begin{eqnarray} R(q)&=&(1+q)(1+q^2)(1+q^4)(1+q^8)~..\\ &=& 1+A q+Bq^2+Cq^3+~..\\ &=&(1+q)R(q^2) \end{eqnarray}
係数比較すると
\begin{eqnarray}  & 1 & ~~~ & q & ~~~ & q^2 & ~~~ & q^3 & ~~~ & q^4 & ~~~ & q^5 &.. \\   & 1 & & A & & B & & C & & D & & E & .. \\ =~& 1 &  &  & & A & & & & B & & & ..\\  &   &  & 1 &   & & & A & & & & B & .. \\  \end{eqnarray}
よって
\begin{eqnarray}  A&=&1\\ B&=&A&,&C&=&A\\ D&=&B&,&E&=&B\\ .. \end{eqnarray}
結局全て１になります。よって
\begin{eqnarray}  R(q)&=&(1+q)(1+q^2)(1+q^4)(1+q^8)~.. \\ &=& 1 + q + q^2 + q^3 + ~.. =\frac{1}{1-q} \end{eqnarray}
$q^k$の係数は$k$を異なる$1,2,4,8,..$で分割する方法の数なので、これが一通りしかないことをこの式は示しています。これは二進数表示が一意であるという証明になっています。

天秤ばかりの問題

さきほどの問題は、天秤ばかりでどんな分銅を持っていれば全ての自然数に対応できるかという問いの答えになります。すなわち1,2,4,8,..という分銅をもっていれば、それの組み合わせで全ての自然数の重さが測れます。しかしこれは天秤の一方だけに分銅をのせる場合の話で、分銅を測りたいものと一緒に乗せてもいいなら、もっと少ない種類の分銅でよくなります。それは1,3,9,27,..という分銅です。これらを引き算と足し算を使って組み合わせることで全ての自然数が表現できます。これをみるため以下のような式を考えます。
\begin{eqnarray}  R(q)&=&(q^{-1}+1+q)(q^{-3}+1+q^3)(q^{-9}+1+q^9)~.. \\ &=& (q^{-1}+1+q)P(q^3) \end{eqnarray}
\begin{eqnarray}  R(q) = ~..+cq^{-3}+bq^{-2}+aq^{-1}+1+Aq+Bq^2+Cq^3+~.. \end{eqnarray}
として係数比較すると
\begin{eqnarray}  &q^{-4} & ~~~ & q^{-3} & ~~~ & q^{-2} & ~~~ & q^{-1} & ~~~ & 1 & ~~~ & q & ~~~ & q^2 & ~~~ & q^3 & ~~~ & q^4 & .. \\   & d && c && b && a && 1 && A && B && C && D &.. \\ =& a && && && 1 && && && A && && &..\\ & && a && && && 1 && && && A && &..\\ & && && a && && && 1 && && && A &.. \end{eqnarray}
よって
\begin{eqnarray}  a&=&1&,&A&=&1\\ a&=&b=c=d&,&A&=&B=C=D\\ b&=&e=f=g&,&B&=&E=F=G\\ .. \end{eqnarray}
よって
\begin{eqnarray}  R(q)&=&(q^{-1}+1+q)(q^{-3}+1+q^3)(q^{-9}+1+q^9)~.. \\ &=& 1+q+q^{-1}+q^2+q^{-2}+q^3+q^{-3}+~..\\ \end{eqnarray}
$q^k$の係数は$k$を異なる$1,3,9,27,..$を足し算と引き算で組み合わせて分割する方法の数です。この方法ですべての整数を一意に表すことができます。