Euclidian Quantum Gravity

0.はじめに

　Physics Lab.では初めまして！東京大学の統合自然科学科に所属しています、3年のRelLimといいます。Physics Lab.2026 Advent Calendar16日目の記事として、Euclidean Quantum Gravityについて紹介します。
　みなさんはブラックホール熱力学という言葉を聞いたことがあるでしょうか。
　ブラックホールは馴染みのある(？)天体かもしれませんが、ブラックホールについての熱力学とはどういうことでしょうか。
　ブラックホールは、その存在がEinsteinの一般相対性理論により予言され、この宇宙に実際に存在することが観測されています。ブラックホールの表面は事象の地平面(Event horizon)とよばれ、ブラックホールの内部に落ち込んでしまったら、強い重力によって光でさえも脱出できません。ブラックホールについては、過去にMathlogにて 「Penrose diagram」 という記事を書いたので興味がありましたらぜひ見てみて下さい！
2022年に観測されたいて座$\text{A}^\ast$のブラックホールシャドウ
　さて、ブラックホールは古典的には外部には何も放出しない天体ですが、Hawkingは、量子効果を考えるならばブラックホールは熱輻射をしていることを示しました。これをHawking輻射と呼びます。すなわち、ブラックホールは温度を持つと考えられるということです。
　温度をもつならば、熱力学みたいな議論ができるのではないか？というモチベーションがブラックホール熱力学の始まりです。ブラックホールの力学法則と熱力学基本法則はかなり似た構造をしており、アナロジーを働かせることで、ブラックホールのエントロピーは表面積に比例すると考えることができます。このようにして考えられたエントロピーをBekenstein-Hawkingエントロピーとよびます。（詳しい議論に興味がある方は、過去に私がまとめた Black hole thermodynamics を見てみてください！）
　この記事では、ブラックホール熱力学へのアプローチの1つである、Euclidian Quantum Gravityについて紹介したいと思います。Hawking温度とBekenstein-Hawkingエントロピーに対して、また違った側面からの導出を紹介していきたいと思います。

1.正則性によるHawking温度の導出

　Hawkingは、重力崩壊する星のPenrose diagramにおいて、漸近的に平坦とみなせる$\mathscr{I}^\pm$でのBogoliubov変換を考えることにより、Hawking温度を導出しました。これは場の量子論に基づく厳密な結果です。しかしながら、厳密ゆえにこの計算はかなり大変なもので、物理的な解釈もなかなか難しいものになっていると感じます。
　そこで第1章では、熱場の理論と幾何学的な性質を用いたより直感的な議論から、Hawking温度を導出することを試みます。

1.1 熱場の理論(Thermal field theory)

　まずは、熱場の理論を紹介します。熱場の理論とは、有限温度における場の量子論です。ブラックホールが存在する背景時空上の場の量子論を考えることによって熱輻射が導かれたため、これを有限温度の場の量子論から見つめ直したいというモチベーションが生まれます。
　ここでは、Wick回転とKMS(Kubo-Martin-Schwinger)条件から、温度効果による虚時間の周期性を導きたいと思います。

1.1.1 Wick回転

　まずは、今後の議論で用いるWick回転について導入しておきます。これは次のような解析接続です。

\begin{align} \quad\quad t\to -i\tau\quad(\tau\in\mathbb{R}) \end{align}

　これは、Minkowski空間をEuclid空間へ置き換える変換に対応します。
\begin{align} \quad\quad -\dd{t}^2+\dd{x}^2+\dd{y}^2+\dd{z}^2 \longrightarrow \dd{\tau}^2+\dd{x}^2+\dd{y}^2+\dd{z}^2 \end{align}

　この$\tau$を虚時間とよびます。
　Wick回転は、Lorentzianな計量をEuclidianな計量に変換することで計算をしやすくすることが一つのモチベーションとしてありますが、特に熱場の理論ではこの虚時間な振る舞いが大切になります。 　

1.1.2 KMS条件

　では、具体的に熱場の理論を考えていきましょう。
　セットアップとして、温度$T$のカノニカル分布にある系を考えます。ハミルトニアンを$H$と置くとき、系の密度演算子$\rho$は次のように書かれます。
\begin{align} \quad\quad \rho=e^{-\beta H} \end{align}

ただし、逆温度$\beta=T^{-1}$を用いました。また、系の分配関数$Z(\beta)$は次のように書かれます。
\begin{align} \quad\quad Z(\beta)=\Tr(e^{-\beta H}) \end{align}

　以上を用いると、熱場の理論における演算子$A$の期待値$\ev{A}_\beta$は次のように計算されます。
\begin{align} \quad\quad \ev{A}_\beta\coloneqq\frac{1}{Z(\beta)}\Tr(Ae^{-\beta H}) \end{align}

　これが期待値になることを確認してみましょう。

　ここで、熱的Green関数を定義します。これは、場の量子論におけるGreen関数の熱場の理論における拡張です。

　ここで、Wick回転を考えます。$t=-i\tau,\:t'=-i\tau'\quad(\tau,\tau'\in\mathbb{R})$とすると、Wick回転した虚時間での熱的Green関数は次のように書かれます。

　また、以下では簡単のために空間成分$x,x'$を省略し、時間成分について議論します。そのため、以降では場の演算子を$O(-i\tau)$、熱的Green関数を$G_\beta(\tau,\tau')$として表します。
　では、熱的Green関数に対して一般的に成立するKMS条件を導きます。

　KMS条件により、逆温度$\beta$のカノニカル分布において、虚時間$\tau$は$\beta$の周期性を持つことが示されます。この本質は、有限温度をもつことが虚時間方向の時間発展とみなせることにあります。また、KMS条件を満たす系は熱平衡状態にあることも示されています⁽¹⁾。
　温度をもつことが虚時間の周期性として表れることが、Hawking温度を幾何学的な側面から導出するカギになります。

1.2 Hawking温度

　では、熱場の理論の枠組みを用いてHawking温度を幾何学的な側面から導出してみます。まずはSchwarzschild時空においてWick回転を行うことで、虚時間に自然に周期性が表れることを見ます。その後、KMS条件よりHawking温度を導出し、Hartle-Hawking stateを紹介します。

1.2.1 Schwarzschild時空における虚時間の周期性

　ここでは、Einstein.eqの球対称真空解であるSchwarzschild時空について考えます。
\begin{align} \quad\quad \dd{s}^2=-\qty(1-\frac{r_s}{r})\dd{t}^2+\qty(1-\frac{r_s}{r})^{-1}\dd{x}^2+r^2\dd{\Omega}_2 \quad\qty(\dd\Omega_2=\dd\theta^2+\sin^2\theta\dd\phi^2) \end{align}
　この時空において、Wick回転$t\to-i\tau$を考えると、次のようになります。
\begin{align} \quad\quad \dd{s}^2=\qty(1-\frac{r_s}{r})\dd{\tau}^2+\qty(1-\frac{r_s}{r})^{-1}\dd{x}^2+r^2\dd{\Omega}_2 \end{align}
　この計量の符号に注目します。このとき、$r>r_s$では$(+,+,+,+)$ですが、$r< r_s$では$(-,-,+,+)$となっています。そのため、$r>r_s$と$r< r_s$は同一の時空として記述できず、「異なる時空」ととらえるのが自然です。よって、以下では計量がEuclidianに振る舞う$r< r_s$の領域について考えます。
　ここで、事象の地平面：$r=r_s$近傍を考えるために次の座標$\rho$を導入します。
\begin{align} \quad\quad &r=r_s+\frac{\rho^2}{4r_s}\quad(\rho\ll r_s) \\ &\Longrightarrow \dd{r}=\frac{\rho}{2r_s}\dd{\rho},\quad1-\frac{r_s}{r}=\frac{\rho^2}{4r_s}+\cdots \end{align}
　これより、$r=r_s$近傍での線素の主要項は次のように表されます。
\begin{align} \quad\quad \dd s^2=\rho^2\frac{\dd{\tau^2}}{4r_s^2}+\dd\rho^2+r_s^2\dd\Omega_2+\cdots \end{align}
　この計量から、事象の地平面近傍の構造は$\mathbb{R}^2\times S^2$となることがわかります。具体的には次のように対応します。
\begin{align} \quad\quad \left\{ \begin{aligned} &\mathbb{R}^2:\dd\rho^2+\rho^2\frac{\dd\tau^2}{4r_s^2} \to \text{2次元平面}\\ &S^2:r_s^2\dd\Omega_2 \quad\quad\quad\to \text{半径$r_sの$2次元球面} \end{aligned} \right. \end{align}
　ここで、$\mathbb{R}^2$に対応する計量に注目すると、これは極座標表示に対応することがわかります。一般的な$\mathbb{R}^2$の極座標$(r,\theta)$との対応を眺めてみると、次のようになります。
\begin{align} \quad\quad \dd r^2+r^2\dd\theta^2\longleftrightarrow\dd\rho^2+\rho^2\frac{\dd\tau^2}{4r_s^2} \end{align}
　これより、$\rho$が動径成分に、$\tau/2r_s$が角度成分に対応することがわかります。前者の対応は、その定義からもかなり自然に感じられますが、後者の対応は非自明です。以下ではこの後者の対応についてさらに議論していきます。
　この対応より、$\tau/2r_s$は周期$2\pi$で同一視される必要があります。

　これが正則性より導かれることを見ます。
　$\tau$が角度成分に対応するために、これに周期性を要請することは自然です。いま、$\tau/2r_s$が周期$2\pi-\delta\:(\delta\neq0)$で同一視されると仮定します。このとき、$\rho-\tau$平面を$\mathbb{R}^3$空間に埋め込むと次の図のようになります。図1中の赤い線は、$\tau/2r_s$の同一視による張り合わせを表しています。
$\mathbb{R}^3$に埋め込まれた$\rho-\tau$平面
　このとき、$\rho=0$は円錐特異点(Conical singurality)となり、Riemannテンソルが発散します。
　これは、Schwarzschild時空がEinstein.eqの真空解であることに反します。Ricciテンソル$R_{\mu\nu}$をEinsteinテンソル$G_{\mu\nu}$を用いて書き直すと次のようになります。
\begin{align} \quad\quad R_{\mu\nu}=G_{\mu\nu}-\frac{1}{2}g_{\mu\nu}g^{\rho\sigma}G_{\rho\sigma} \end{align}
　真空解では、Einstein.eqより$G_{\mu\nu}=0$であるため、$R_{\mu\nu}=0$となります。しかしながら、円錐特異点がある場合は、その点においてRiemannテンソルが発散するためにこれが成立しません。そのため、円錐特異点の存在は真空解に矛盾します。よって、$\delta=0$となる必要があり、$\tau/2r_s$には$2\pi$の周期性が要請されることになります。 　

1.2.2 Hawking温度の導出

　1.2.1の議論により、Schwarzschild時空における虚時間$\tau$には$4\pi r_s$の周期性があることがわかりました。
　ここで、熱場の理論におけるKMS条件を思い出しましょう。KMS条件により、温度$T$のカノニカル分布で記述される系において、虚時間は$\beta=1/T$の周期性をもちます。また、この逆についても成立することを述べました。
　さて、この議論をSchwarzschild時空に適用すると、次が言えます。

　ブラックホールの質量を$M$としたとき、事象の地平面は$r_s=2M$となることから、温度$T_H$は次のように書かれます。
\begin{align} \quad\quad T_H=\frac{1}{8\pi M} \end{align}
　このようにして、Hawking温度が虚時間の周期性から導かれました！

　ここまでの議論の流れをもう一度たどってみます。
　Wick回転をした計量に対して$r< r_s$の領域を考え、真空解であるために正則性(Regularity)が要請されて、虚時間に周期性が現れました。よって、次の座標と計量によって記述される空間は完全に正則であるといえます。

　これをSchwarzschild時空のEuclidian切断とよびます。この空間を直感的につかむために、$\theta,\phi$を固定した2次元超平面を考えます。これは、$\tau$の周期性と$r=r_s$での正則性から次のようになります。

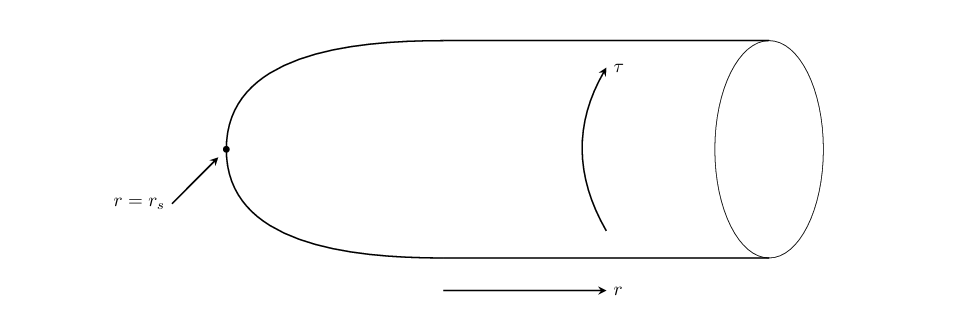Schwarzschild時空のEuclidian section

　$r$が大きい領域では、ほぼ円筒のような構造になり、$r\to r_s$では、その正則性から滑らかに閉じています。この幾何的な構造を、その形状からよく「葉巻のような構造」とよんだりします。
　また、Schwarzschild時空に立ち返ると、$r< r_s$の領域は$r=r_s$においてブラックホールに接していました。事象の地平面の外側の量子場が温度$T_H$の熱平衡状態にあるため、ブラックホールもまた温度$T_H$をもつ必要があります。これは、ブラックホールが物質を吸収すると同時に輻射を行う平衡状態にあると解釈されます。この状態のことをHartle-Hawking stateとよびます。

2. 経路積分によるブラックホールのエントロピーの導出

　第2章では、ブラックホール熱力学におけるもっとも重要な結果と言えるBekenstein-Hawkingエントロピーを、経路積分を用いたアプローチから導出していきます。
　古典的には、Bekenstein-Hawkingエントロピーは、ブラックホールが温度をもつことから熱力学的な取り扱いができると考え、ブラックホールの力学法則と熱力学基本法則の間にアナロジーを働かせることで導かれていました。本章では、これを重力場の作用から見つめ直します。
　重力場の作用に対する経路積分について扱い、Euclidian on-shell actionを議論することで境界項が本質的な役割を果たすことを見ていきましょう。

2.1 Euclidian重力経路積分

　重力場の作用に対する積分を扱うために、まずは分配関数の経路積分表示を考えます。その後、これを拡張して重力場の作用に対する経路積分を考えていきます。

2.1.1 分配関数の経路積分表示

　熱場の理論における分配関数を思い出してみましょう。温度$T=\beta^{-1}$のカノニカル分布にある系のハミルトニアンを$H$と置くとき、この系の分配関数$Z(\beta)$は次の形で表されていました。
\begin{align} \quad\quad Z(\beta)=\Tr e^{-\beta H} \end{align}
　ハミルトニアンが場の演算子$\phi$で書かれているとして、これを場の演算子の固有状態$\ket{\phi}$を用意すると、分配関数は次のように書かれます。
\begin{align} \quad\quad Z(\beta)=\int\mathcal{D}\phi \ev{e^{-\beta H}}{\phi} \end{align}
　ここで、温度が虚時間の時間発展であるとみなせることを思い出しましょう。つまり、$e^{-\beta H}$は虚時間における時間発展演算子であると思えば、場の量子論における経路積分への移行と全く同じ手続きを行うことができます。
　系のLagrangian密度が
\begin{align} \quad\quad \mathcal{L}=\frac{1}{2}\partial^2\phi-\frac{1}{2}m^2\phi^2-V(\phi) \end{align}のような形で書かれているならば、経路積分表示は次のように書かれるはずです。
\begin{align} \quad\quad Z(\beta) &= \int\mathcal{D}\phi\exp\qty[-\int_0^\beta\mathrm{d}\tau\mathrm{d}x^3\mathcal{L}_\text{E}] \\ &= \int\mathcal{D}\phi\exp\qty[-I_\text{E}(\beta)] \quad\qty(I_E(\beta)\coloneqq\int_0^\beta\mathrm{d}\tau\mathrm{d}x^3\mathcal{L}_\text{E}) \end{align}
　ただし、Wick回転をしてEuclid化したLagrangian密度を$\mathcal{L}_\text{E}$と書き、これによる作用を$I_\text{E}$としました。注意点は、虚時間は周期性があるため、$\tau$の積分範囲が$[0,\beta]$になっていて、作用が$\beta$に依存しているところです。

2.1.2 重力場の作用に対する経路積分

　それでは、ここまでの議論を拡張して重力場の作用を含めた経路積分を考えます。
　重力場を含めた作用$I$は、物質場$\phi$と計量$g_{\mu\nu}$についての汎関数になっています。そのため、分配関数は次のように表現されると考えられます。
\begin{align} \quad\quad Z=\int\mathcal{D}g_{\mu\nu}\mathcal{D}\phi \exp\qty(-I[g_{\mu\nu},\phi]) \end{align}
　ただし、Wick回転をしてEuclidianな空間として計算します。これは、1.2.2で見たように、計量が特異に振る舞わない領域で経路積分を実行することができるためです。
　では、これを計算してしまえばよいわけなのですが、そう簡単に計算できるものではありません。そのため、この経路積分を、古典的な運動方程式の解まわりでの鞍点近似によって評価することを考えます。
　場$g_{\mu\nu},\phi$を、古典的な運動方程式を満たす項$\bar{g}_{\mu\nu},\bar{\phi}$とそこからの摂動項$\delta g_{\mu\nu},\delta\phi$に分けます。
\begin{align} \quad\quad g_{\mu\nu}=\bar{g}_{\mu\nu}+\delta g_{\mu\nu},\quad\phi=\bar{\phi}+\delta\phi \end{align}
　これを用いて作用を次のように展開します。
\begin{align} \quad\quad I\qty[g_{\mu\nu},\phi]=I[\bar{g}_{\mu\nu},\bar{\phi}]+I_2\qty[\delta g_{\mu\nu},\delta\phi]+\cdots \end{align}
　第1項$ I[\bar{g}_{\mu\nu},\bar{\phi}]$が古典的な作用に、第2項$I_2\qty[\delta g_{\mu\nu},\delta\phi]$は2次の摂動項に、それ以降の項はより高次の摂動項に対応します。この展開を用いると、経路積分は次のように評価できます。
\begin{align} \quad\quad -\log Z=I[\bar{g}_{\mu\nu},\bar{\phi}]+\log\int\mathcal{D}\delta g_{\mu\nu}\mathcal{D}\delta\phi\exp(-I_2\qty[\delta g_{\mu\nu},\delta\phi])+\cdot \end{align}
　第1項が、鞍点まわりでの分配関数での主要項になり、第2項は2次の摂動に対する経路積分で、これは1ループの量子補正に対応します。
　ここからは、この量子補正を落とし、分配関数の主要項である$ I[\bar{g}_{\mu\nu},\bar{\phi}]$について詳しく議論していきます。

2.2 Einstein-Hilbert作用

　では、鞍点近似で評価するために、古典的な作用であるEinstein-Hilbert作用について具体的に議論しましょう。
\begin{align} \quad\quad I_{\text{EH}}\coloneqq-\frac{1}{16\pi}\int_\mathcal{M}\mathrm{d}^4x\sqrt{g}R \end{align}
　ただし、$g\coloneqq\det g_{\mu\nu}$、$\mathcal{M}$は時空全体であり、これはWick回転をしてEuclidianな作用にしてあります。
　Schwarzschild時空では、$R=0$であるため、この作用をそのまま用いても何かおもしろい結果が得られそうにありません。さらに、時空の体積は無限大であるため、このままでは長距離発散が現れます。そこで、時空は有限の値$r=r_0$まで広がっていると仮定します。これはいわゆるカットオフとしての役割を果たし、計算の最後において$r_0\to\infty$の極限をとります。時空の広さを有限と置いたため、時空は$r=r_0$において境界$\partial\mathcal{M}$を持ちます。
　さて、この過程においては境界条件をさらに深く考える必要があります。$I_\text{EH}$に対して$g_{\mu\nu}$で変分をとりEinstein.eqを導出する過程を眺めてみましょう。具体的な計算過程はAppendixに譲るとして、作用の変分は次の形になります。
\begin{align} \quad\quad \delta I_\text{EH} =-\frac{1}{16\pi}\int_\mathcal{M} \mathrm{d}^4x\sqrt{g}\qty(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R)\delta g^{\mu\nu}-\frac{1}{16\pi}\int_{\partial\mathcal{M}}\dd{\Sigma}_\rho\sqrt{g}\qty(g^{\mu\nu}\delta\Gamma^\rho{}_{\mu\nu}-g^{\mu\rho}\delta\Gamma^\nu{}_{\mu\nu}) \end{align}
　ただし、$\mathrm{d}\Sigma_\rho$は境界$\partial\mathcal{M}$の微小面積要素としました。第一項に、Einsteinテンソルが現れていて、Einstein.eqの気配を感じます。しかし、ここで注目するべきは第2項の存在です。Christoffel記号$\Gamma^\rho{}_{\mu\nu}$の変分を含むということは、この項は計量の変分$\delta g_{\mu\nu}$と、計量の一回微分の変分$\delta(\partial g_{\mu\nu})$を含みます。これが実は問題なのです。
　変分原理では、計量$g_{\mu\nu}$を端点にて固定するDirichlet境界条件のもとで計算するため、$\delta(\partial g_{\mu\nu})$を0とすることはできません。つまり、このままでは実はEinstein.eqは導かれないのです。基本的には時空は無限に広いとして、$\partial\mathcal{M}$を無限遠に飛ばすことで、その境界上では$\delta\Gamma^\rho{}_{\mu\nu}=0$として良いだろうと思ってEinstein.eqを導くことが多いと思いますが、これは物理的には厳しい要請であり、悪い言い方をすれば「誤魔化している」といえます。さらに、今回は発散を回避するために時空を有限領域と仮定する必要があり、なおさら不自然です。そのため、必然的に境界項を導入して作用を変更する必要があるのです。この境界項について詳しく見ていきましょう。

2.2.1 Gibbons-Hawking-York境界項

　ここでは、作用に対して次のGibbons-Hawking-York境界項を導入します。

　ただし、$y$は$\partial\mathcal{M}$の3次元座標、$h_{\mu\nu}$は$\partial\mathcal{M}$での誘導計量、$K\coloneqq h^{\mu\nu}K_{\mu\nu}$は外曲率$K_{\mu\nu}$のトレースです。$\partial\mathcal{M}$の外向きの単位法線ベクトルを$n^\mu$としたとき、誘導計量$h_{\mu\nu}$と外曲率$K_{\mu\nu}$は次で得られます。
\begin{align} \quad\quad h_{\mu\nu}&=g_{\mu\nu}-n_\mu n_\nu\\ K_{\mu\nu}&=\nabla_\mu n_\nu \end{align}
　この境界項を含めた$I\coloneqq I_\text{EH}+I_\text{GHY}$に対して変分原理を適用すると、問題になっていた変分がキャンセルされて、Dirichlet境界条件のみからEinstein.eqが得られます(詳しい計算はAppendixに譲りました)。よって、これを改めてEinstein-Hilbert作用として定義しておきましょう。

　それでは、この作用を用いて鞍点近似を計算していきましょう。
　Euclidian切断をしたSchwarzschild時空で、$K$を計算します。$\partial\mathcal{M}$は$r=r_0$の3次元超曲面であるから、誘導計量と法線ベクトルは次のようになります。
\begin{align} \quad\quad &h_{ij}\dd y^i\dd y^j=\qty(1-\frac{r_s}{r})\dd\tau^2+r^2\dd\Omega_2 \\ & n^\mu = \qty(1-\frac{r_s}{r})^{1/2}\delta^\mu_r \end{align}
　また、外曲率のトレースは次のように計算できます。
\begin{align} \quad\quad K &= h^{\mu\nu}K_{\mu\nu} \\ &= \qty(g^{\mu\nu}-n^\mu n^\nu)\nabla_\mu n_\nu \\ &= \nabla_\mu n^\mu-\frac{1}{2}n^\mu\nabla_\mu\qty(n^\nu n_\nu) \\ &= \nabla_\mu n^\mu\quad(\because n^2=\text{Const.}) \\ &= \frac{1}{\sqrt{g}}\partial_\mu\qty(\sqrt{g}n^\mu) \end{align}　
　これらより、$\partial\mathcal{M}$の外曲率は次のようになります。
\begin{align} \quad\quad K&=\left. \frac{1}{r^2\sin\theta}\partial_r\qty({r^2\sin\theta\sqrt{1-\frac{r_s}{r}}})\right|_{r=r_0} \\ &=\left. \frac{1}{r^2}\partial_r\qty[r^2\qty(1-\frac{r_s}{2r}-\frac{r_s^2}{8r^2}-\frac{r_s^3}{16r^3}\cdots)]\right|_{r=r_0} \\ &=\left.\frac{1}{r^2}\qty(2r-\frac{r_s}{2})+\mathcal{O}(r^{-4})\right|_{r=r_0} \\ &=\frac{2}{r_0}-\frac{r_s}{2r_0^2}+\mathcal{O}(r_0^{-4}) \end{align}

　これより、GHY項が次のように得られます。
\begin{align*} \quad\quad-\frac{1}{8\pi}\int_{\partial\mathcal{M}}\mathrm{d}^3y\sqrt{h}K &= \left. -\frac{1}{8\pi}\int^\beta_0\dd\tau\int^\pi_0\dd\theta\int^{2\pi}_0\dd\phi\:r^2\sin\theta\sqrt{1-\frac{r_s}{r}}K\right|_{r=r_0} \\ &= -\frac{1}{8\pi}\cdot 4\pi\beta\qty(2r_0-\frac{2r_s}{r_0})\qty(1-\frac{r_s}{2r_0}-\cdots) \\ &= \beta\qty(-r_0+\frac{3}{4}r_s)+\mathcal{O}(r_0^{-1}) \end{align*}

　これで計算が完了！めでたしめでたし！とはならないのが、ここからの難しいところです。2.2の冒頭でも述べたように、最後に$\partial\mathcal{M}$を無限遠に飛ばす極限をとる必要があります。しかしこの式を見ると、境界項は$r_0\to\infty$で発散してしまいます。この発散を取り除くためのカウンター項はどうすればよいでしょうか。

2.2.2 Einstein-Hilbert作用の繰り込み

　そこで、「平坦時空の寄与を差し引いて繰り込む」というアイデアを考えます。私たちは時空が曲がっていることによる効果を見たいため、（作用）＝（Schwarzschild時空だから出てくる部分）＋（平坦時空でも出てくる部分）と分解して、その後者を取り除こうというのがモチベーションです。黒体輻射のエネルギーを計算するときに、調和振動子の真空エネルギーを引いてしまうこととやりたいことは同じです。
　平坦時空として、$r=r_0$で$\partial\mathcal{M}$と同じような構造をもつものを選ぶのが適切なので、次のような計量をここでは選択しましょう。
\begin{align} \quad\quad \dd s^2_\text{flat} &= \dd r^2+\qty(1-\frac{r_s}{r_0})\dd\tau^2+r^2\dd\Omega_2 \\ &\eqqcolon \dd r^2+h_{ij}^\text{flat}\dd x^i\dd x^j \end{align}
　この計量は確かに平坦時空に対応します。また、平坦時空の$r=r_0$の超平面$\Sigma$での誘導計量$h_{ij}^\text{flat}$が、Schwarzschild時空の$\partial\mathcal{M}$での誘導計量$h_{ij}$に一致することも明らかです。それでは、この超平面$\Sigma$を境界にもつ平坦時空による作用への寄与$I_\text{flat}$を計算してみましょう。
　平坦時空のため、Ricciスカラーは0になります。そのため$I_\text{flat}$は境界項のみを計算すればよいことになります。平坦時空の計量を$g_{\mu\nu}^\text{flat}$、$\Sigma$の外曲率を$K_{\mu\nu}^\text{flat}$、外向きの単位法線ベクトルを$n_\mu^\text{flat}$と置けば、次のように計算されます。
\begin{align} \quad\quad g^\text{flat}&\coloneqq\det g_{\mu\nu}^\text{flat} \\ &= \qty(1-\frac{r_s}{r_0})r^4\sin^2\theta \\ h^\text{flat}&\coloneqq\det h_{\mu\nu}^\text{flat} \\ &= \qty(1-\frac{r_s}{r_0})r^4\sin^2\theta \\ n^\mu_\text{flat} &= \delta^\mu_r\\ K^\text{flat}&\coloneqq h^{\mu\nu}_{\text{flat}}K_{\mu\nu}^\text{flat} \\ &= \frac{1}{\sqrt{g^\text{flat}}}\partial_\mu\qty(\sqrt{g^\text{flat}}n^\mu_\text{flat}) \\ &= \frac{1}{\sqrt{g^\text{flat}}}\partial_r\qty(\sqrt{g^\text{flat}}) \\ &= \frac{1}{r^2}\partial_rr^2 \\ &= \frac{2}{r} \end{align}
　よって、$I_\text{flat}$は次のようになります。
\begin{align} \quad\quad I_\text{flat} &\coloneqq -\frac{1}{8\pi}\int_\Sigma \mathrm{d}^3y\sqrt{h^\text{flat}}K^\text{flat} \\ &= \left. -\frac{1}{8\pi}\int^\beta_0\dd\tau\int^\pi_0\dd\theta\int^{2\pi}_0\dd\phi\:2r\sin\theta\sqrt{1-\frac{r_s}{r_0}}\right|_{r=r_0} \\ &= \left. -\frac{1}{8\pi}\cdot4\pi\beta\cdot2r\sin\theta\sqrt{1-\frac{r_s}{r_0}}\right|_{r=r_0} \\ &= \beta\qty(-r_0+\frac{1}{2}r_s)+\mathcal{O}(r_0^{-1}) \end{align}
　以上を踏まえて、繰り込まれたEinstein-Hilbert作用$I_\text{ren}$を次のように定義します。

　このようにすると、発散項を取り除くことができます。次でこれを確認してみましょう。

2.3 Euclidian on-shell actionとBekenstein-Hawkingエントロピー

　それでは、2.2の結果を用いて、鞍点近似によって分配関数を計算してみましょう。
　ここでは、繰り込まれたEinstein-Hilbert作用をSchwarzschild時空で評価すればよいです。これをEuclidian on-shell action$I_\text{on-shell}$とよびます。on-shellとは「古典解を満たす」という意味であり、ここではEinstein.eqの真空解のことを指しています。Schwarzschild時空の場合の作用は2.2ですべて計算したので、これを代入してみましょう。
\begin{align} \quad\quad I_\text{on-shell}&=0-\beta\qty(-r_0+\frac{3}{4}r_s)+\beta\qty(-r_0+\frac{1}{2}r_s)+\mathcal{O}(r_0^{-1}) \\ &= \frac{1}{4}\beta r_s \\ &= \frac{\beta^2}{16\pi} \quad(\because\beta=4\pi r_s) \end{align}

　すると、確かにこの作用は$r_0$に依らないため、$r_0\to\infty$としても発散しません。これでようやく分配関数$Z(\beta)$を鞍点近似で計算できます。
\begin{align} \quad\quad -\log Z(\beta)\sim I_\text{on-shell}=\frac{\beta^2}{16\pi} \end{align}

　分配関数さえ計算できればもうこちらのものです。自由エネルギー$F$と内部エネルギー$E$を計算してみます。
\begin{align} \quad\quad F&=-\frac{1}{\beta}\log Z(\beta)=\frac{\beta}{16\pi} \\ E&=-\frac{\partial}{\partial\beta}\log Z(\beta)=\frac{\beta}{8\pi}=M \end{align}
　これらより、エントロピー$S$は次のようになります。
\begin{align} \quad\quad S&=\beta(E-F) \\ &= \frac{\beta^2}{16\pi} \\ &= \pi r_s^2\\ &= \frac{\mathcal{A}}{4} \quad(\mathcal{A}\coloneqq 4\pi r_s^2) \end{align}
　このようにして、Bekenstein-Hawkingエントロピーが確かに導かれました！

3.おわりに

　今回は、半古典近似の下での重力経路積分で得た分配関数から、Bekenstein-Hawkingエントロピーを導出しました。重力を完全に量子的に扱うことはまだできませんが、半古典近似の下でも非常に重要な洞察を得ることができます。近年は、この文脈でIsland formulaと呼ばれる非常に重要な結果が得られています(筆者である私もこれは勉強中です( ˙ ˙ *)ﾜｸﾜｸ…!!)。ますます今後の発展が楽しみです。
　ここまで読んでくださったそこのあなたも、重力と遊んでみませんか？ありがとうございました！

Appendix

　詳しい計算を一応載せました。
　そんなに大事でもないので、興味があったら見てみてください。
　途中で使っている公式1,2はAppendix.Cの公式集に載せています。

Appendix.A Einstein-Hilbert作用の変分

　Einstein-Hilbert作用の変分を計算してみます。
\begin{align}   \quad\quad\delta I_\text{EH}   =-\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}R_{\mu\nu}\delta g^{\mu\nu}   -\frac{1}{16\pi}\int\mathrm{d}^4 xR\delta\sqrt{g}   -\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}g^{\mu\nu}\delta R_{\mu\nu} \end{align}

　右辺の第2項を詳しく計算してみます。ここで、$g_{\mu\nu}$の行列式の変分について次が成立します。
\begin{align}   \quad\quad\delta g=g g^{\alpha\beta}\delta g_{\alpha\beta} \end{align}

　この結果から、$\sqrt{g}$の変分は次のように計算されます。
\begin{align*}   \quad\quad\delta\sqrt{g} &= \frac{1}{2\sqrt{g}}\delta g \\   &= \frac{1}{2}\sqrt{g}g^{\mu\nu}\delta g_{\mu\nu} \end{align*}

　添え字の上下をそろえるために、次のように変換します。
\begin{align*}   \quad\quad\delta g_{\mu\nu}&=\delta\qty(g_{\mu\alpha}g_{\nu\beta}g^{\alpha\beta}) \\   &= \delta^\alpha_\nu\delta g_{\mu\alpha}+\delta^\beta_\mu\delta g_{\nu\beta}+g_{\mu\alpha}g_{\nu\beta}\delta g^{\alpha\beta} \\   \therefore  \delta g_{\mu\nu}&=-g_{\mu\alpha}g_{\nu\beta}\delta g^{\alpha\beta} \end{align*}

　これらより、Einstein-Hilbert作用の変分は次のように整理されます。
\begin{align}   \quad\quad\delta I_\text{EH}   =-\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}\qty(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R)\delta g^{\mu\nu}   -\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}g^{\mu\nu}\delta R_{\mu\nu}   \end{align}

　ではRicciテンソルの変分の計算をします。天下り的ですが、次を計算してみます。
\begin{align*}   \quad\quad&\nabla_\alpha\qty(\delta\Gamma^\alpha{}_{\mu\nu})-\nabla_\nu\qty(\delta\Gamma^\alpha{}_{\mu\alpha}) \\   =&\qty(\partial_\alpha\delta\Gamma^\alpha{}_{\mu\nu}+\Gamma^\alpha{}_{\rho\alpha}\delta\Gamma^\rho{}_{\mu\nu}-\Gamma^\rho{}_{\mu\alpha}\delta\Gamma^\alpha{}_{\rho\nu}-\Gamma^\rho{}_{\nu\alpha}\delta\Gamma^\alpha{}_{\mu\rho}) \\   &\quad-\qty(\partial_\nu\delta\Gamma^\alpha{}_{\mu\alpha}+\Gamma^\alpha{}_{\rho\nu}\delta\Gamma^\rho{}_{\mu\alpha}-\Gamma^\rho{}_{\mu\nu}\delta\Gamma^\alpha{}_{\rho\alpha}-\Gamma^\rho{}_{\alpha\nu}\delta\Gamma^\alpha{}_{\mu\rho}) \\   =&\partial_\alpha\delta\Gamma^\alpha{}_{\mu\nu}-\partial_\nu\delta\Gamma^\alpha{}_{\mu\alpha}+\Gamma^\alpha{}_{\rho\alpha}\delta\Gamma^\rho{}_{\mu\nu}+\Gamma^\rho{}_{\mu\nu}\delta\Gamma^\alpha{}_{\rho\alpha}-\Gamma^\rho{}_{\mu\alpha}\delta\Gamma^\alpha{}_{\rho\nu}-\Gamma^\alpha{}_{\rho\nu}\delta\Gamma^\rho{}_{\mu\alpha} \\   =&\delta R_{\mu\nu} \end{align*}
　ただし、Christoffel記号の変分がテンソルとして振る舞うことを用いました。

　これを用いると、Einstein-Hilbert作用の変分の第3項は次のように整理されます。
\begin{align*}   \quad\quad&\int\mathrm{d}^4 x\sqrt{g}g^{\mu\nu}\delta R_{\mu\nu} \\   =&\int\mathrm{d}^4 x\sqrt{g}g^{\mu\nu}\qty[\nabla_\alpha\qty(\delta\Gamma^\alpha{}_{\mu\nu})-\nabla_\nu\qty(\delta\Gamma^\alpha{}_{\mu\alpha})] \\   =&\int\mathrm{d}^4 x\sqrt{g}\qty[\nabla_\alpha\qty(g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\nu})-\nabla_\nu\qty(g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\alpha})] \\   =&\int\mathrm{d}^4 x\qty[\partial_\alpha\qty(\sqrt{g}g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\nu})-\partial_\nu\qty(\sqrt{g}g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\alpha})] \\   =&\oint_{\partial\mathcal{M}}\mathrm{d}\Sigma_\alpha\sqrt{g}\qty(g^{\mu\nu}\delta\Gamma^{\alpha}{}_{\mu\nu}-g^{\mu\alpha}\delta\Gamma^\nu{}_{\mu\nu}) \end{align*}
　ただし、公式2を用い、最後の変形でGaussの法則を適用しました。
　以上により、Einstein-Hilbert作用の変分は次のようにまとめられます
\begin{align}   \quad\quad\delta I_\text{EH}   =-\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}\qty(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R)\delta g^{\mu\nu}   -\frac{1}{16\pi}\oint_{\partial\mathcal{M}}\mathrm{d}\Sigma_\alpha\sqrt{g}\qty(g^{\mu\nu}\delta\Gamma^{\alpha}{}_{\mu\nu}-g^{\mu\alpha}\delta\Gamma^\nu{}_{\mu\nu}) \end{align}

Appendix.B Gibbons-Hawking-York境界項の計算

　先ほどの変分の表面積分項をさらに計算してみます。以下明記しませんが、すべて境界$\partial\mathcal{M}$上で計算します。
　境界$\partial\mathcal{M}$においては、Dirichlet境界条件をとっていることから$\delta g_{\mu\nu}=0$であるため、次のように計算されます。
\begin{align*}   \quad\quad &g^{\alpha\nu}\delta\Gamma^{\mu}{}_{\alpha\nu}-g^{\mu\nu}\delta\Gamma^\alpha{}_{\nu\alpha} \\   =&\frac{1}{2}\qty[g^{\mu\nu}g^{\rho\sigma}\qty(\partial_\mu\delta g_{\sigma\nu}+\partial_\nu\delta g_{\mu\sigma}-\partial_\sigma\delta g_{\nu\mu})-g^{\mu\rho}g^{\nu\sigma}\qty(\partial_\mu\delta g_{\sigma\nu}+\partial_\nu\delta g_{\mu\sigma}-\partial_\sigma\delta g_{\mu\nu})] \\   =&\frac{1}{2}\qty[g^{\mu\nu}g^{\rho\sigma}\qty(\partial_\mu\delta g_{\sigma\nu}+\partial_\nu\delta g_{\mu\sigma}-\partial_\sigma\delta g_{\nu\mu})-g^{\mu\nu}g^{\rho\sigma}\qty(\partial_\sigma\delta g_{\mu\nu}+\partial_\nu\delta g_{\mu\rho}-\partial_\mu\delta g_{\sigma\nu})] \\   =&g^{\mu\nu}g^{\rho\sigma}\qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) \end{align*}

　これより、$\dd{\Sigma}_\mu\sqrt{g}=\mathrm{d}^3y n_\mu\sqrt{h}$としたときの法線ベクトル$n^\mu$を合わせると次が成立します。
\begin{align*}   \quad\quad&n_\alpha\qty(g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\nu}-g^{\mu\alpha}\delta\Gamma^\nu{}_{\mu\nu}) \\   =&n^\sigma g^{\mu\nu}\qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) \\   =&n^\sigma \qty(h^{\mu\nu}+n^\mu n^\nu)\qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) \\   =&n^\sigma h^{\mu\nu}\qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) + s^\sigma s^\mu s^\nu \qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) \\   =&n^\sigma h^{\mu\nu}\qty(\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}) \end{align*}

　ただし、最後の式変形では、$s^\sigma s^\mu$は$\mu\leftrightarrow\sigma$の入れ替えに対して対称であるが、$\partial_\mu\delta g_{\sigma\nu}-\partial_\sigma\delta g_{\mu\nu}$は反対称であることを用いました。
　また、$\partial\mathcal{M}$上では$\delta g_{\mu\nu}=0$であるため、$\partial_\sigma\delta g_{\mu\nu}$の$\partial\mathcal{M}$上への射影もまた0になるため、次のように整理されます。
\begin{align*}  \quad\quad n_\alpha\qty(g^{\mu\nu}\delta\Gamma^\alpha{}_{\mu\nu}-g^{\mu\alpha}\delta\Gamma^\nu{}_{\mu\nu})=-n^\sigma h^{\mu\nu}\partial_\sigma\delta g_{\mu\nu} \end{align*}

　以上をまとめると、Einstein-Hilbert作用の表面積分項は次のように整理されます。
\begin{align}  \quad\quad\int_{\partial\mathcal{M}}\mathrm{d}\Sigma_\alpha\sqrt{g}\qty(g^{\mu\nu}\delta\Gamma^{\alpha}{}_{\mu\nu}-g^{\mu\alpha}\delta\Gamma^\nu{}_{\mu\nu})=-\int\mathrm{d}^3y\sqrt{h}n^\sigma h^{\mu\nu}\partial_\sigma\delta g_{\mu\nu} \end{align}

　次に、Gibbons-Hawking-York境界項の変分を計算します。
　外曲率のトレース$K$について整理されます。
\begin{align*}   \quad\quad K&\coloneqq h^{\mu\nu}\nabla_\mu n_\nu \\   &= h^{\mu\nu}\qty(\partial_\mu n_\nu-\Gamma^\sigma{}_{\mu\nu}n_\sigma) \end{align*}

　$\partial\mathcal{M}$上では$\delta g_{\mu\nu}=0\to\delta h_{\mu\nu}=0$であり、また、$\delta n_\mu=0$であるから、$\partial_\sigma \delta g_{\mu\nu},\partial_\mu n_\nu$の$\partial\mathcal{M}$上への射影は0になります。これらより$K$の変分は次のように計算されます。
\begin{align*}   \quad\quad\delta K &= -h^{\mu\nu}(\delta\Gamma^\sigma{}_{\mu\nu})n_\sigma \\   &= -\frac{1}{2}h^{\mu\nu}g^{\rho\sigma}\qty(\partial_\mu\delta g_{\rho\nu}+\partial_\nu\delta g_{\mu\rho}-\partial_\rho\delta g_{\mu\nu})n_\sigma \\   &= \frac{1}{2}n^\sigma p^{\mu\nu}\partial_\sigma\delta g_{\mu\nu} \end{align*}

　これより、Gibbons-Hawking-York境界項の変分は次のようになります。
\begin{align*}   \quad\quad\delta I_\text{GHY}&=-\frac{1}{8\pi}\delta\int_{\partial\mathcal{M}}\mathrm{d}^3y\sqrt{h}K \\   &=-\frac{1}{16\pi}\int_{\partial\mathcal{M}}\mathrm{d}^3y\sqrt{h}n^\sigma p^{\mu\nu}\partial_\sigma\delta g_{\mu\nu} \end{align*}

　以上から、境界項を含めたEinstein-Hilbert作用の変分は次のようになります。
\begin{align*}   \quad\quad\delta(I_\text{EH}+I_\text{GHY}) &= -\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}\qty(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R)\delta g^{\mu\nu} \\   &\quad\quad\quad\quad+\int\mathrm{d}^3y\sqrt{h}n^\sigma h^{\mu\nu}\partial_\sigma\delta g_{\mu\nu}-\int\mathrm{d}^3y\sqrt{h}n^\sigma h^{\mu\nu}\partial_\sigma\delta g_{\mu\nu} \\   &= -\frac{1}{16\pi}\int\mathrm{d}^4 x\sqrt{g}\qty(R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R)\delta g^{\mu\nu} \end{align*}
　すると、たしかに綺麗に表面積分項がキャンセルされて、真空の場合のEinstein.eqが導かれます。　

Appendix.C 便利な公式集

　一般相対論の計算をするときにいろんなところで頻出します。名前がついていないのによく使うので、私は「便利な公式」とよく書いたりします。

\begin{align} \quad\quad \end{align}