Gradient flowによる微分方程式の数値計算

【修正履歴】

• 08May2024: 「$\omega$粒子により安定化したSkyrmion」の章の数値計算を正しいものに修正しました。また当該の章の「問題1」の式を修正しました（第1式左辺最後の項の分母を$m_\pi\to m_\omega$とした）。さらにその次の四角いテキストボックスの中の式を実用的に使いやすい形に書き換え、その下の当該式の説明を修正しました。

Gradient flow

本記事ではgradient flowと呼ばれる微分方程式の解法について説明します。呼び方は他にもあるかもしれませんが、ここではRef.Mantonに従いこのように呼びます。

微分方程式と汎関数の極小化

微分方程式と汎関数の極小化は密接に関係します。力学におけるLagrange形式はその典型例です。ある時刻$t$における物体の位置$x(t)$を、作用と呼ばれる$x(t)$の汎関数$S(x(t))$の$x(t)$に関する極小化で求めます。$S(x(t))$はLagrangian $L(x(t),\dot x(t))$の積分として
\begin{align} S(x(t))=\int dt L(x(t),\dot x(t)) \end{align}
と書かれます（ドットは時間微分）。一般には$L$は時刻$t$に陽に依存してもいいですが、ここでは陽には依存しないとします。$S(x(t))$の極値は$S(x(t))$を変分してゼロになる$x(t)$で与えられます。このとき$x(t)$は
\begin{align} \delta S(x(t))=0 \leftrightarrow \frac{d}{dt}\left( \frac{\partial L}{\partial \dot x} \right)-\frac{\partial L}{\partial x} =0 \end{align}
を満たします。$\leftrightarrow$の右辺の式はEuler-Lagrange方程式 (EL-eq.)と呼ばれます（※脚注）。

空間$\boldsymbol{x}$および時刻$t$に依存する何らかの場$\phi(x^\mu) \ (x^\mu:=(t,x,y,z))$の運動や状態も同様に最小作用の原理で書かれます。作用$S(\phi)$がLagrangian密度なる量$\mathcal{L}(\phi,\partial_\mu \phi)$の4次元積分で書かれるとします：
\begin{align} S(\phi):=\int d^4x \mathcal{L}(\phi,\partial_\mu \phi) \end{align}
$\partial_\mu \ (\mu=0,1,2,3)$とは$\partial_\mu=(\partial_t,\partial_x,\partial_y,\partial_z)$のことです。このときEL-eq.は
\begin{align} \partial_\mu \left(\frac{\partial\mathcal{L}}{\partial(\partial_\mu\phi)}\right) -\frac{\partial\mathcal{L}}{\partial\phi}=0 \ \ \ \ (\mu\mathrm{は和を取る}) \end{align}
です。静的な場の場合、空間座標$\boldsymbol{x}$のみに依存する関数$\phi(\boldsymbol{x})$のエネルギー汎関数$E(\phi(\boldsymbol{x}),\partial_i\phi(\boldsymbol{x}))$の極小化に帰着します（後述）。

Gradient flow

改めて以下の問題を考えます：
${}$
$\hspace{5cm}$$\xi(x)$に依存する汎関数$\Xi(\xi(x),\partial_x\xi(x))$を極小化し、$\xi(x)$を決定する
${}$
もちろんEL-eq.に相当する微分方程式を求め、それを解いて$\xi(x)$を決定してもよいです。一方で、微分方程式を解くかわりに、各$x$において$\Xi(\xi(x))$が最も下がる方向に$\xi(x)$を変形していくことで$\xi(x)$を求めることもできます。これがgradient flowの方法です。数値計算をするために$x$を離散化し、これを$x_i(i=1,\ldots N)$とすると、$\Xi$は$\xi_i:=\xi(x_i)$の多変数関数になります。こうすると汎関数微分は多変数関数$\Xi(\xi_i)$の偏微分になります。初期の$\xi^{(0)}_i$を用意し、これを$-\partial \Xi(\xi_i)/\partial \xi_i$(gradient descent)の方向に漸次落としていくことで$\Xi$を極小化する$\xi_i$を求めます。

最近の流行との対比でいうと、やっていることは機械学習における目的関数の極小化と同じです。

Gradient flowの利点: 境界値問題

微分方程式を直接解くことと比較したとき、gradient flowの方法のメリットはなんでしょうか。

微分方程式は境界条件が与えられて初めて解けます。数値計算では、$\xi(r)$の2階微分方程式なら2つの境界条件: $\xi(r=\mathrm{boundary}), \xi'(r=\mathrm{boundary})$を用い、差分化した方程式（＝漸化式）を使って端から解を構成します。

問題は境界条件が両端で与えられる場合です。物理学では往々にして$\xi(r=0)$と$\xi(r=\infty)$の値が与えられ、傾きがわからないことがあります。このような場合によく使われるのがシューティング法です。この方法では片側の境界条件を適当に与えてそれを変えながら解を構成し、逆側の境界条件を満たす解を探します。例えば$\xi'(r=0)$を適当に与えて解を$r$が大きいところまで構成し、$\xi(r=\text{large})$が与えられた値に近づくように$\xi'(r=0)$を調整します。非常にシンプルでわかりやすい方法です。しかし時に、解が$\xi,\xi'$の境界条件に非常に鋭敏であり、少し境界の値が違うだけで解が大きく変わってしまう場合があります。この場合たまごを机に立てるのにも似た繊細なチューニング作業が必要になります。また連立微分方程式のように求める解が複数存在する場合、シューティングのパラメータが複数になるため、パラメータ空間中の適切なパラメータの範囲が非常に狭くなり、とてつもないファインチューニングが必要になります。

このような場合に便利なのがgradient flowです。前述したように、この方法では最初に与えられた境界条件を満たす適当な関数を用意します。この初期の場を、系の汎関数を下げる方向に漸次変化させていくことで汎関数の極小解を求めます。$\xi$と$\xi'$の両方を知る必要はありません。初期の関数はもちろん真の解に近いほうがいいですが、特にトポロジカルな保存量がある場合などは、けっこう雑な初期関数でもちゃんと真の解に収束します。のちほどそのような具体例を示します。

Gradient flowのformalism

Gradient flowの方程式は非常にシンプルであり、以下で与えられます：
\begin{align} \kappa\partial_\tau\xi(x,\tau)=-\frac{\delta \Xi(\xi)}{\delta\xi(x,\tau)} \end{align}
ここで$\tau$は仮想時間です。$\xi$を$\tau=0$から発展させ、大きな$\tau$において$\xi(x,\tau)$の$\tau$に対する変化が止まれば、それが$\Xi$の極小を与える解です。

以下静的な場の配位を考えます。改めて$\xi$を$\phi$と書き直します。この場合汎関数$\Xi$は静的なエネルギーに対応するので、これを改めて$E(\phi)$で表します。これはラグランジアンの符号を反対にしたもので与えられます：$E(\phi)=-\int d^3x {\cal L}(\phi,\partial_i\phi)$（$i$は空間方向の足）。 $E(\phi)$の変分を計算すれば
\begin{align} \delta E(\phi) &=-\int d^3x\left( \frac{\partial{\cal L}}{\partial\phi}\delta \phi +\frac{\partial{\cal L}}{\partial(\partial_i\phi)}\delta(\partial_i\phi) \right)\\ &=-\int d^3x\left[\frac{\partial{\cal L}}{\partial\phi} -\partial_i\left(\frac{\partial{\cal L}}{\partial(\partial_i\phi)}\right)\right]\delta\phi\\{}\\ \therefore &-\frac{\delta E(\phi)}{\delta \phi} =\frac{\partial{\cal L}}{\partial\phi} -\partial_i\left(\frac{\partial{\cal L}}{\partial(\partial_i\phi)}\right) \end{align}
を得ます。右辺イコールゼロは$\phi$に対するEL-eq.にほかなりません (※符号に注意)。よって配位が運動方程式を満たす場合仮想時間に対する$\phi$の発展は止まり、正しい解が求まることがわかります。

静的な配位に対してラグランジアンが${\cal L}=-\frac{1}{2}{\boldsymbol \nabla}^2\phi-V(\phi)$（$V(\phi)$:ポテンシャル項）で与えられるとすれば
\begin{align} -\frac{\delta E(\phi)}{\delta \phi} ={\boldsymbol \nabla}^2\phi-\frac{\partial V}{\partial\phi} \end{align}
になります。

以上よりこの場合gradient flowの方程式は以下で与えられます：
\begin{align} \kappa\partial_0\phi&=\frac{\partial{\cal L}}{\partial\phi} -\partial_i\left(\frac{\partial{\cal L}}{\partial(\partial_i\phi)}\right)\\ \kappa\partial_0\phi&={\boldsymbol \nabla}^2\phi-\frac{\partial V}{\partial\phi} \ \ \ \ \ \left({\cal L}=-\frac{1}{2}{\boldsymbol \nabla}^2\phi-V(\phi)\text{の場合} \right) \end{align}
ここでは仮想時間の微分を$\partial_0$としました。ポテンシャルが下がる方向に$\phi$を落としていくので、ポテンシャルの$\phi$微分の符号は負です。$\partial_0\phi$を離散化すれば、それは1回の更新で$\phi$がどれだけ変化するかを表しています。更新を何度も繰り返し$\phi$が収束すれば、求める解が得られます。のちほど具体例を示します。

不安定性

gradient flowの計算においてひとつ気をつけるべきことがあります。それは不安定性です。前章の方程式は熱伝導方程式と同様の形をしています。そしてこの系には数値計算で不安定性が生じることが知られていますNeumann。

前述のgradient flowの方程式に含まれる$\kappa$は、1回の更新でどれだけ配位が変わるかを司るパラメータです。$\kappa$が小さい方が1回の更新による配位の変化が大きいので良いように思うかもしれません。しかし$\kappa$が小さいと不安定性が起きます。空間方向の分割幅に対し$\kappa$を十分大きくしておかないと、初期配位のフーリエモードの高周波成分がどんどん増幅されて数値計算が全くうまくいきません。このような現象が起きるときには$\kappa$を大きくして計算してください。必然更新回数は多くなります。

ちなみに機械学習でよく使われる最小化のアルゴリズムであるAdamを用いると、単純な最急降下法と比較し、不安定性が抑えられ更新回数が少なくて済むこともあります。

実際の数値計算

以下具体的にgradient flowの方法を説明するため、以下の文献

1. John C.Neu, "Vortices in Complex Scalar Fields," Physica D43, 385-406 (1990). Neu
2. G.S.Adkins, C.R.Nappi, "STABILIZATION OF CHIRAL SOLITONS VIA VECTOR MESONS," Physics Letters 137B 3,4 (1984). Adkins

に現れる非線形微分方程式をgradient flowで計算します。数値計算の話に焦点を当てるため、数学的・物理的な背景は基本的に省くことをご了承ください。

1. 非線形Schrödinger方程式における静的なvortex解

まずはNeuの文献の数値計算を行います。

2-dim.において次の微分方程式を解きます：
\begin{align} {\boldsymbol \nabla}^2\psi+(1-|\psi|^2)\psi=0 \end{align}
これは非線形Schrödinger方程式または非線形熱拡散方程式の静的なバージョンですNeu。

この系には渦の解 −vortex解− が存在します。これを求めるため、以下のansatzをおきます:
\begin{align} \psi({\boldsymbol x})=U(r)\exp[i(n\theta+\theta_0)] \tag{1} \end{align}
ここで$(r,\theta)$は2-dim.の極座標、$\theta_0$は任意定数、$n$はvortexのwinding numberです。これを上記の微分方程式に代入すると以下の方程式を得ます:
\begin{align} U''+\frac{1}{r}U'-\frac{n^2}{r^2}U+(1-U^2)U=0 \end{align}
ここでプライムは$r$微分を表します。境界条件は以下で与えられます：
\begin{align} U(r=0)=0, \ U(r=\infty)=1 \end{align}
以下この静的なvortex解を数値的に求めることを考えます。

Gradient flowの方程式

$\phi$および$U$に対するgradient flow eqs.は以下のようになります：
\begin{align} \kappa\partial_0\phi&={\boldsymbol \nabla}^2\phi+(1-\bar\phi\phi)\phi,\\ \kappa \partial_0 U&=U''+\frac{1}{r}U'-\frac{n^2}{r^2}U+(1-U^2)U \end{align}
$\partial_0$を離散化し、方程式を以下のように書き換えておきます：
\begin{align} U_{\rm new}=U+\alpha \left\{ U''+\frac{1}{r}U'-\frac{n^2}{r^2}U+(1-U^2)U\right\} \tag{2} \end{align}
こうすればgradient flow eq.を解くことは、EoMに係数をかけて元の配位に加えたものを新たな配位$U_{\textrm{new}}$とする作業を繰り返すことと等価であることがわかります。

数値計算の結果

実際にEq.(1)の1回巻き($n=1$)の解を求めてみます。そのためはまず、適切な境界条件 (Boundary Condition, BC) を持つ初期配位を用意してやります。

前記したようにBCは$U(r=0)=0, \ U(r=\infty)=1$で与えられます。さらに解の漸近形が以下のようになることがわかっていますNeu：
\begin{align} U^{(n)}(r)&\sim ar^{|n|}+{\cal O}(r^{|n|+2}) \hspace{1.1cm} \ \ \text{as} \ \ r\to 0,\\ &\sim 1-n^2/r^2+{\cal O}(1/r^4) \ \ \ \text{as}\ \ r\to\infty \end{align}
これらより初期配位として良さげな関数形のひとつは$\tanh$であることがわかります。実際にRef.Neuのグラフを読み取り$\tanh$でフィットすると
\begin{align} U(r)=\tanh(0.54795 r) \end{align}
程度がよいことがわかります。ちなみにグラフから数値を読み取る際WPDは便利です。

実際の初期配位は解からずらして
\begin{align} U^{\rm init}(r)=\tanh(0.3r) \end{align}
を用いて計算を始めます。

計算に用いたパラメータは以下です：

N=200, dr=0.05, reg=0.001,$\alpha$=0.001, Niter=4000

ここでNは区間の分割数、drは$r$の分割幅、$\alpha$はEq.(2)の式中の係数、regは$r=0$での発散を避けるパラメータ、Niterは$U_{\textrm{new}}$の計算の繰り返しの回数です。また$U'$および$U''$を各iterationの段階で計算しなければならないため、$U(r)$の両端の「さらに1点先」まで値が必要です。これに関しては両端の値をそのまま「その1点先」に使っています。すなわちNeumann BCを用いています。

これらのパラメータを用いてEq.(2)を繰り返し用い解を求めます。これをグラフにしたのが図1です。
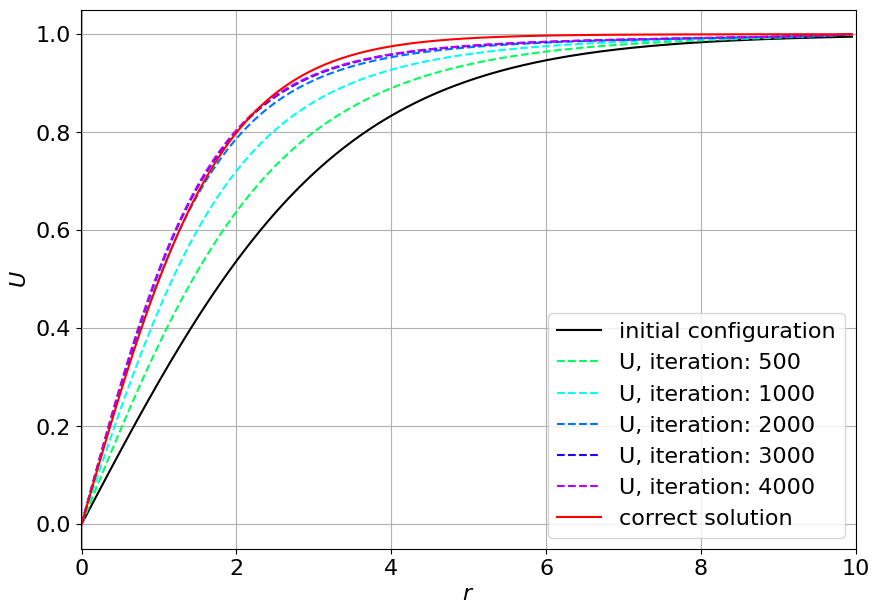vortex解のiterationへの依存性

黒実線は初期配位 ($\tanh(0.3r)$)、赤実線はEq.(1)の解（Ref.Neu）、破線がEq.(2)を繰り返し適用して得られた$U$です。図のキャプションにある"iteration"は各破線に対応する繰り返しの数です。この図から、始め真の解に大きく近づき、その後徐々に解付近に収束していく様子がわかります。iterationが4000でも真の解から少しずれていますが、様々な要因が考えられるためあまり気にしないでください。$\alpha$は前述した不安定性が起こらない程度に小さく取ります。

不安定性にさえ気をつければ、いいかげんな初期配位から始めても正しい解に収束します（図2および図3）。
初期配位を$\tanh(0.01r)$とした場合の$U$のiteration numberに対する変化 。
初期配位を$\tanh(10.0r)$とした場合の$U$のiteration numberに対する変化

図2では初期配位（黒実線）が$r=10$で1よりかなり小さな値となっています。いまBCはDirichletであり、図の両端からdrだけ離れた点（0-drおよび10+dr）における$U$の値を、初期配位を外挿して作成し用いています。よって図2では右端の$U$の値は1よりかなり小さな値で固定されています。それでも正しい解に収束するので、少なくともこの系ではかなり適当な初期配位を用意しても大丈夫なようです。これは$n=\pm 1$の解がトポロジカルに安定な解であることも関係していると思います(Ref.Neu)。

しかしながら初期条件に対する安定性は系に大きく依存するでしょうし、また方程式には自明な解$U(r)\equiv 0$も存在するので、初期配位には気を遣う方が賢明だと思います。

2. $\omega$粒子により安定化したSkyrmion

実は前章の例ではシューティング法を用いても簡単に解を求めることができます（確かそうだったと思います）。本章ではシューティング法では解を求めることが難しい系Adkinsを扱います。

Skyrme模型と呼ばれる、核子を記述する有効模型があります。これは非線形シグマ模型と呼ばれる系にSkyrme項を付加した模型です。この系にはSkyrmionと呼ばれるソリトン解が存在し、これは核子とみなすことができます。これに関しては記事にしていますのでそちらをご参照くださいSkyrmion。

非線形シグマ模型単独では安定したソリトン解は存在しないことが知られています。そこにSkyrme項を加えることで安定した解が存在しますSkyrmion。一方、Skyrme項ではなく、ベクトル粒子との相互作用を加えることで安定化させることもできますAdkinsZahed。ここでは$\omega$粒子と呼ばれるベクトル中間子を加えることでソリトン解を安定化させます。このソリトンをRef.Zahedにならい以下"$\omega$-stabilized Skyrmion"と呼ぶことにします。

詳細は省きますが、パイオン場の非線形表現$ U=\exp((2i/F_\pi)\boldsymbol{\tau}\cdot\boldsymbol{\pi})$（$\boldsymbol{\pi}:=(\pi^1,\pi^2,\pi^3)$はパイオン場。1,2,3の足はアイソスピンの足。$\boldsymbol{\tau}:=(\tau^1,\tau^2,\tau^3)$はパウリ行列。$F_\pi:$はパイオン崩壊定数）に関してはHedgehog ansatz
\begin{align} U=\exp(i\boldsymbol{\tau}\cdot\hat{\boldsymbol{x}}f(r)) \end{align}
を用います（$\hat{\boldsymbol{x}}:=\boldsymbol{x}/||\boldsymbol{x}||$）。ベクトルメソンである$\omega$粒子の場$\omega_\mu$に関してはその時間成分のみが存在するとして$\omega:=\omega_0$とします。自然単位系を採用し、すべての次元を持つ量をパイオン崩壊定数: $F_\pi=186\mathrm{MeV}$で測ると、$f,\omega$に関して以下の方程式が成立しますAdkins：
\begin{align} r^2f''+2rf'-(\sin 2f + m_\pi^2 r^2\sin f)+\frac{4\bar\beta}{m_\pi}\omega'\sin^2 f=0,\\ -r^2\omega''-2r\omega'+m_\omega^2r^2\omega=\frac{\bar\beta}{m_\omega} f'\sin^2f \end{align}
$r$は3次元極座標の動径座標、プライムは動径座標による微分、$m_\pi,m_\omega$はそれぞれパイオンおよび$\omega$粒子の質量とします。すべて$F_\pi$の単位で測られていることに注意してください。$m_\pi,m_\omega$はそれぞれ
\begin{align} m_\pi&=138\mathrm{MeV}/186\mathrm{MeV}=0.7419,\\ m_\omega&=782\mathrm{MeV}/186\mathrm{MeV}=4.204 \end{align}
です。また$r=1$は$1.061\mathrm{fm}$、すなわちだいたい$1\mathrm{fm}$です。そして$\bar\beta$は自由なパラメータとします。

境界条件は、パイオン場に関しては1回巻きの解を求めるので$f(0)=\pi,\ f(\infty)=0$、$\omega$に関しては$\omega(0):\mathrm{finite},\ \omega(\infty)=0$としますAdkins。

Ref.Adkinsでは$\bar\beta=1,5,10$に対して$r=4$付近（$\simeq 4\mathrm{fm}$）まで解を構成しています。$r=0$での傾きの情報がないですが、$\bar\beta=1,5$に関しては$r=0$からシューティング法を使って解を構成できます。しかしやってみればわかりますが、$\bar\beta=10$に関しては$r=4$付近まで解を構成するのはなかなか難しいです。

そこでgradient flowで解を構成してみます。この系のgradient flowの方程式は以下で与えられます。

$0\le r\le 5.4$の範囲で分割数$N=600$、分割の1区間の長さ$dr=0.009$で計算しました。また$\alpha_f = 0.000008, \alpha_\omega = 0.000008$とし、iterationの回数は$200000$としました。また初期の$f,\omega$の配位として、$\bar\beta=1.0$ではそれぞれ
\begin{align} f^{(\mathrm{init},\bar\beta=1)}(r) &=\frac{\pi}{1+0.5618r+14.12r^2},\\ \omega^{(\mathrm{init},\bar\beta=1)}(r) &=-\frac{1}{1+67.41r^4} \end{align}
を用いました。そして$\bar\beta=5.0$では$\bar\beta=1.0$の解、$\bar\beta=10.0$では$\bar\beta=5.0$の解を初期配位として用いています。

vortexの場合と同様、$f,\omega$の微分を両端の点で計算するため、両端の「1点先」の点が必要です。これに関しては、$f$の$r=0$における「1点先」は$\pi$で固定し、あとはNeumann BCを用いています。

図4が計算結果のグラフです。

$f(r),\omega(r)$の$\bar\beta=1,5,10$に対するグラフ。薄緑の点線及び点破線はそれぞれ$\beta=1.0$の計算時の$f$と$\omega$の初期配位を表す。

オレンジの線、水色の線、赤の線がそれぞれ$\bar\beta=1, 5, 10$に対応します。また太線（正の値の解）が$f(r)$、細い線（負の値の解）が$\omega(r)$に対応します。タイトルの$\alpha$は上に出てきた$\alpha_f,\alpha_\omega$のことです。薄い緑の点線および点破線は、それぞれ$\beta=1$における$f$と$\omega$の初期配位です。縦軸の$\omega$は質量次元1の量であり、$F_\pi$の単位で測っています（$f$は次元なし）。また横軸は文献と合わせるため$\mathrm{fm}$の単位でプロットしています。gradient flowを用いると$\bar\beta=10$でも解が求まり、かつRef.Adkinsと結果が一致します。iterationが20万回と多いのは、不安定性を避けるため1回の更新による配位変化を小さくしているためです。しかしこれだけ計算しても計算時間は短いです（今回使用したコードでは、1つの$\bar\beta$に対し10秒程度）。

この計算では$\beta=1.0$における$f$の初期配位の漸近形はある程度良いものを使わないと正しい解に辿り着きません。本計算ではRef.Adkinsの図から漸近形をフィットして使っています。これは$r$の大きい方の境界でNeumann BCを使っていることが関係していると思います。また$\alpha_{f,\omega}$はあまりに小さいとやはり正しい解に辿り着きません。当然ではありますが、gradient flowでも計算結果の各種パラメータに対する依存性はきちんと調べて収束性を確認しなければなりません。

ちなみにこの系では、$f$の配位が定まると、$\omega$の配位はGreen関数
\begin{align} G(r,r')=(2m_\omega rr')^{-1} \{ \exp(-m_\omega|r-r'|)-\exp(-m_\omega(r+r')) \} \end{align}
を用いて
\begin{align} \omega(r)&=\int_0^\infty dr'G(r,r') \left[-\frac{2\pi^2\bar\beta}{m_\omega} r'^2 B^0(r')\right], \\ B^0&=-\frac{1}{2\pi^2}\frac{f'\sin^2 f}{r^2} \end{align}
で与えられますAdkins。これを用いてシューティングやgradient flowを行うとより簡単に解を得ることができると思います。

まとめ

本記事では微分方程式を数値計算で解く際に有用であるgradient flowの方法に関して説明しました。Gradient flowの方法は、例えば境界条件で微分の値がわからないときなどに有用であり、特にシューティング法がうまく機能しないときには威力を発揮します。2つの例 −2-dim.におけるvortex解および$\omega$-stabilized Skyrmion− に関して具体的に数値計算を行い、両系で比較的簡単に解を構成できることを説明しました。

本記事では静的な場のみを扱い、汎関数として静的なエネルギーを扱いました。一方作用$S$に対してgradient flowを適用すれば、原理的には時間発展も求まるはずです。ただそのような例はあまり見たことがないので、うまく解が求まるかはよく知りません。

「Gradient flowのformalism」の章を見ればわかるのですが、Euler-Lagrange方程式さえわかっていれば、gradient flowの方程式を作ることは簡単です。計算アルゴリズムも非常に単純です。通常の方法で微分方程式が数値的に解けない場合、試してみるとよいかもしれません。

需要があるかわかりませんが、計算に使用したコードをGistに置いておきますcode_vortexcode_Skyrmion。プロット用コードも添付してあります。jupyter notebookにコードをコピペして使うと便利かと思います。

おしまい。${}_\blacksquare$

${}$

【脚注】 これは極値条件なので、実際には極大である可能性もあります。その場合解は不安定であり、安定性の議論が必要になります。