Tietzeの拡張定理

1. 写像$F$の定義より
   \begin{align} x \in \mathrm{LHS} &\iff \inf\{r \in D \mid x \in X(r)\} < t\\ &\iff \exists r \in D,\ x \in X(r),\ r < t\\ &\iff x \in \mathrm{RHS} \end{align}
   が成り立つ．
2. 1. $x \in \mathrm{LHS}$とし，$s \in D, t < s$とする．このとき$F(x) < s$より，$r \in D$であって$x \in X(r),\,r < s$なるものが存在するので，
      $$ x \in X(r) \subset X(s)$$
      が成り立つ．よって$x \in \mathrm{RHS}$を得る．
   2. $x \in \mathrm{RHS}$とする．もし$t < F(x)$であるとすると，$D \subset [0,1]$の稠密性より，$s \in D$であって$t < s < F(x)$なるものが存在する．このとき仮定より$x \in X(s)$であるが，
      $$ F(x) \leq s < F(x)$$
      となって不合理である．

$\tau([0,1])$の準開基の元の$F$による逆像が$X$の開集合であること，すなわち任意の$t \in [0,1]$に対して，
$$ F^{\leftarrow}([0,t[\,) \subset X$$
が開集合であること，および
$$ F^{\leftarrow}([0,t]) = X \smallsetminus F^{\leftarrow}(\,]t,1]) \subset X$$
が閉集合であることを示せばよい．

1. 1. inv-imgより
      \begin{align} F^{\leftarrow}([0,t[\,) &= \{x \in X \mid F(x) < t\}\\ &= \bigcup \{X(r) \mid r \in D,\ r < t\} \subset X \end{align}
      は開集合である．
   2. まづ
      $$ \bigcap \{X(s) \mid s \in D,\ t < s\} \subset \bigcap \{\cl(X(r)) \mid r \in D,\ t < r\}$$
      が成り立つことに注意する．逆に，$x \in \mathrm{RHS}$とし，$s \in D, t < s$とすると，$r \in D$であって$t < r < s$なるものが存在するので，
      $$ x \in \cl(X(r)) \subset X(s)$$
      が成り立ち，したがって$x \in \mathrm{LHS}$を得る．よってinv-imgより，
      \begin{align} F^{\leftarrow}([0,t]) &= \{x \in X \mid F(x) \leq t\}\\ &= \bigcap \{X(s) \mid s \in D,\ t < s\}\\ &= \bigcap \{\cl(X(r)) \mid r \in D,\ t< r\} \subset X \end{align}
      は閉集合である．
2. 1. まづ
      $$ \bigcup \{X(r) \mid r \in D,\ r < t\} \supset \bigcup \{\I(X(s)) \mid s \in D,\ s < t\}$$
      が成り立つことに注意する．逆に，$x \in \mathrm{LHS}$とすると，$r \in D, r < t$であって$x \in X(r)$なるものが存在するので，$s \in D$であって$r < s < t$なるものを取れば
      $$ x \in X(r) \subset \I(X(s)) \subset \mathrm{RHS}$$
      が成り立つ．よってinv-imgより
      \begin{align} F^{\leftarrow}([0,t[\,) &= \{x \in X \mid F(x) < t\}\\ &= \bigcup \{X(r) \mid r \in D,\ r < t\}\\ &= \bigcup \{\I(X(s)) \mid s \in D,\ s < t\} \subset X \end{align}
      は開集合である．
   2. inv-imgより
      \begin{align} F^{\leftarrow}([0,t]) &= \{x \in X \mid F(x) \leq t\}\\ &= \bigcap \{X(s) \mid s \in D,\ t < s\} \subset X \end{align}
      は閉集合である．

$a,b \in [0,1],a< b,$とする．このとき$n \in \mathbb{N}$であって
$$ \frac{1}{2^{n}} < b-a$$
なるものが存在する．いま
$$ a \in [0,1[\, = \bigcup_{i=0}^{2^{n}-1} \left[\frac{i}{2^{n}}, \frac{i+1}{2^{n}}\right[$$
であるから，$i \in [2^{n}-1] := \{0,\ldots,2^{n}-1\}$であって
$$ a \in \left[\frac{i}{2^{n}},\frac{i+1}{2^{n}}\right[$$
を満たすものが存在する．よって$r := (i+1)2^{-n} \in D$とおくと，
$$ a < r = \frac{i}{2^{n}} + \frac{1}{2^{n}} \leq a + \frac{1}{2^{n}} < b$$
が成り立つ．

(i)$\implies$(ii)

$A := X \smallsetminus W$とおくと，$A,C \subset X$は互いに交わらない閉集合なので，$U \in \tau(A,X), V \in \tau(C,X)$であって$U \cap V = \varnothing$を満たすものが存在する．このとき
$$ V \subset X \smallsetminus U \in \tau^{c}(X)$$
より，
$$ \cl(V) \subset X \smallsetminus U \subset X \smallsetminus A = W$$
が成り立つ．

(ii)$\implies$(iii)

$N := \cl(V)$とおけば
$$ C \subset V \subset \I(N) \subset N \subset W$$
が成り立つ．

(iii)$\implies$(i)

$W := X \smallsetminus A$とおくと，これは$C$の開近傍なので，$C$の閉近傍$N \subset X$であって$N \subset W$を満たすものが存在する．このとき，
$$ A = X \smallsetminus W \subset X \smallsetminus N$$
より，$U:= X \smallsetminus N \in \tau(X)$は$A$の開近傍であって$U \cap \I(N) = \varnothing$を満たす．

Step. 0

各$r \in D$に対して
$$ U_{A}(r) := \{x \in A \mid f(x) < r\} \subset \{x \in A \mid f(x) \leq r\} =: A(r)$$
とおく．$A(r) \subset X$は閉集合であることに注意する．また，
$$ U(r) := (X\smallsetminus A) \cup U_{A}(r) = X \smallsetminus f^{\leftarrow}([r,1]) \in \tau(X)$$
とおくと，
$$ r < s \implies A(r) \subset U(s)$$
が成り立つ．最後に，
$$ \Delta := \{(r,s) \in D \times D \mid r < s\}$$
とおき，
$$ (r',s') < (r,s) :\iff (r' < r) \land (s' < s)$$
と定める．

Step. 1

$((r_{n},s_{n}))_{n \in \mathbb{N}}$を$\Delta$の元の数え上げとする．$X$の開集合族$(W(r,s))_{(r,s) \in \Delta}$であって

1. $A(r) \subset W(r,s) \subset \cl(W(r,s)) \subset U(s)$;
2. $(r',s') < (r,s) \implies \cl(W(r',s')) \subset W(r,s)$;

を満たすものを，次のようにして定める：

1. $A(r_{0}) \subset U(s_{0})$に対して，cl-nhdより，開集合$W(r_{0},s_{0}) \in \tau(X)$であって
   $$ A(r_{0}) \subset W(r_{0},s_{0}) \subset \cl(W(r_{0},s_{0})) \subset U(s_{0})$$
   を満たすものが存在する．
2. $(W(r_{i},s_{i}))_{i \in [n]}$まで定まったとする．そこで
   $$ \Delta_{n} := \{(r_{0},s_{0}),\ldots,(r_{n},s_{n})\}$$
   とおいて，閉集合$C_{n+1} \subset X$と開集合$O_{n+1} \subset X$を
   \begin{align} C_{n+1} &:= A(r_{n+1}) \cup \bigcup\{\cl(W(r',s')) \mid (r',s') \in \Delta_{n},\ (r',s') < (r_{n+1},s_{n+1})\},\\ O_{n+1} &:= U(s_{n+1}) \cap \bigcap\{W(r,s) \mid (r,s) \in \Delta_{n},\ (r_{n+1},s_{n+1}) < (r,s)\} \end{align}
   で定める．明らかに$A(r_{n+1}) \subset U(s_{n+1})$であり，任意の$(r,s) \in \Delta_{n},(r_{n+1},s_{n+1}) < (r,s),$に対して
   $$ A(r_{n+1}) \subset A(r) \subset W(r,s)$$
   が成り立つので，$A(r_{n+1}) \subset O_{n+1}$を得る．また，$(r',s') \in \Delta_{n}, (r',s') < (r_{n+1},s_{n+1}),$とすると，
   $$ \cl(W(r',s')) \subset U(s') \subset U(s_{n+1})$$
   であり，任意の$(r,s) \in \Delta_{n},\ (r_{n+1},s_{n+1}) < (r,s),$に対して，$(r',s') < (r,s)$より
   $$ \cl(W(r',s')) \subset W(r,s)$$
   が成り立つので，$\cl(W(r',s')) \subset O_{n+1}$を得る．以上より
   $$ C_{n+1} \subset O_{n+1}$$
   が成り立つので，cl-nhdより，開集合$W(r_{n+1},s_{n+1}) \in \tau(X)$であって
   $$ C_{n+1} \subset W(r_{n+1},s_{n+1}) \subset \cl(W(r_{n+1},s_{n+1})) \subset O_{n+1}$$
   を満たすものが存在する．$C_{n+1},O_{n+1}$の定め方より，開集合族$(W(r_{i},s_{i}))_{i \in [n+1]}$は明らかに所期の条件を満たす．

Step. 2

$X$の閉被覆$(X(r))_{r \in D}$を
$$ X(r) := \begin{cases} \bigcap\{\cl(W(r,s)) \mid s \in D,\ r < s\} &, r < 1\\ X &, r = 1 \end{cases}$$
で定める．このとき

1. $r < s \implies X(r) \subset \I(X(s))$;
2. $A \cap X(r) = A(r)$;

が成り立つことを示す．

Step. 2-1

$(r,s) \in \Delta$とする．
$$ X(r) \subset X = \I(X(1))$$
であるから，$s < 1$としてよい．$D \subset [0,1]$の稠密性より，$s' \in D$であって$r < s' < s$なるものが存在する．このとき，$(r,s') < (s',s)$より，
$$ X(r) \subset \cl(W(r,s')) \subset W(s',s)$$
が成り立つ．一方，
$$ X(s) = \bigcap \{\cl(W(s,t)) \mid t \in D,\ s < t\}$$
であった．そこで$t \in D, s < t,$とすると，$(s',s) < (s,t)$より
$$ W(s',s) \subset \cl(W(s',s)) \subset W(s,t) \subset \cl(W(s,t))$$
が成り立つ．よって，
$$ W(s',s) \subset \bigcap\{\cl(W(s,t)) \mid t \in D,\ s < t\} = X(s)$$
となるので，
$$ X(r) \subset W(s',s) \subset \I(X(s))$$
が成り立つ．

Step. 2-2

$r \in D$とする．
$$ A \cap X(1) = A = A(1)$$
であるから，$r < 1$としてよい．

1. 任意の$s \in D, r < s,$に対して
   $$ A(r) \subset W(r,s) \subset \cl(W(r,s))$$
   が成り立つので，
   $$ A(r) \subset A \cap X(r)$$
   を得る．
2. 逆に，
   \begin{align} A \cap X(r) &\subset A \cap \bigcap\{U(s) \mid s \in D,\ r < s\}\\ &= \bigcap \{A \cap U(s) \mid s \in D,\ r < s\}\\ &= \bigcap \{U_{A}(s) \mid s \in D,\ r < s\}\\ &\supset A(r) \end{align}
   が成り立つが，$D \subset [0,1]$の稠密性より，
   $$ \bigcap\{U_{A}(s) \mid s \in D,\ r < s\} \subset A(r)$$
   も成り立つ．

以上より
$$ A \cap X(r) = A(r)$$
が成り立つ．

Step. 3

写像$\tilde{f} \colon X \to [0,1]$を
$$ \tilde{f}(x) := F_{(X(r))_{r\in D}}(x) = \inf\{r \in D \mid x \in X(r)\}$$
で定めると，contiより，これは連続写像である．あとは$\tilde{f}|A = f$を示せばよい．そこで$x \in A$とする．

1. 任意の$r \in D,x \in X(r)$に対して，
   $$ x \in A \cap X(r) = A(r)$$
   より，$f(x) \leq r$となるので，
   $$ f(x) \leq \tilde{f}(x)$$
   が成り立つ．
2. もし$f(x) < \tilde{f}(x)$であるとすると，$D \subset [0,1]$の稠密性より，$r \in D$であって$f(x) < r < \tilde{f}(x)$なるものが存在するが，このとき
   $$ x \in U_{A}(r) \subset A(r) = A \cap X(r) \subset X(r)$$
   より
   $$ \tilde{f}(x) \textcolor{orange}{\leq} r < \tilde{f}(x)$$
   となり不合理である．

写像$g \colon A_{0} \sqcup A_{1} \to [0,1]$を
$$ g(x) := \begin{cases} 0 &, x \in A_{0}\\ 1 &, x \in A_{1} \end{cases}$$
で定めると，これは連続であるから，tietzeより，連続写像$f \colon X \to [0,1]$であって$f|A_{0} \sqcup A_{1} = g$を満たすものが存在する．明らかに
$$ f^{\rightarrow}(A_{0}) \subset \{0\},\ f^{\rightarrow}(A_{1}) \subset \{1\}$$
が成り立つ．

連続写像$\varphi \colon \mathbb{R} \rightleftarrows \,]-1,1[\, \colon \psi$を
$$ \varphi(r) := \frac{2}{\pi}\arctan(r);\ \psi(s) := \tan\qty(\frac{\pi s}{2})$$
で定めると，これらは互いの逆写像である．そこで
$$ f_{0} := \id_{]-1,1[}^{[-1,1]} \circ \varphi \circ f \colon A \to \mathbb{R} \approx \,]-1,1[\, \subset [-1,1]$$
とおくと，tietzeより，連続写像$\tilde{f_{0}} \colon X \to [-1,1]$であって$\tilde{f_{0}}|A = f_{0}$を満たすものが存在する．いま，
$$ A_{0} := \tilde{f_{0}}^{\leftarrow}(\{-1,1\}) \subset X$$
は$A$と交わらない閉集合であるから，urysohnより，連続写像$g \colon X \to [0,1]$であって
$$ g^{\rightarrow}(A_{0}) \subset \{0\},\ g^{\rightarrow}(A) \subset \{1\}$$
を満たすものが存在する．このとき，任意の$x \in X = A_{0} \cup (X \smallsetminus A_{0})$に対して
$$ \tilde{f_{0}}(x) g(x) \in \,]-1,1[$$
が成り立つので，連続写像$\tilde{f} \colon X \to \mathbb{R}$を
$$ \tilde{f}(x) := \psi(\tilde{f_{0}}(x)g(x))$$
で定めることができる．この$\tilde{f}$が$f$の連続拡張を与えている．実際，$x \in A$とすると，$g(x) = 1$より，
$$ \tilde{f}(x) = \psi(\tilde{f_{0}}(x)) = \psi(f_{0}(x)) = \psi(\varphi(f(x))) = f(x)$$
が成り立つ．

開集合族$(X(r))_{r \in D}$であって
$$ r< s \implies A_{0} \subset X(r) \subset \cl(X(r)) \subset X(s) \subset X \smallsetminus A_{1}$$
を満たすものを，$r \in D_{n}$となる$n \in \mathbb{N}$に関して帰納的に定める：

1. 閉集合$A_{0} \subset X$の開近傍$X \smallsetminus A_{1} \in \tau(A_{0},X)$に対して，cl-nhdより，$V \in \tau(A_{0},X)$であって
   $$ \cl(V) \subset X \smallsetminus A_{1}$$
   を満たすものが存在する．そこで
   $$ X(0) := V,\ X(1) := X \smallsetminus A_{1}$$
   とおく．
2. $r := (2i+1)2^{-(n+1)} \in D_{n+1}\smallsetminus D_{n}$とする．いま
   $$ \cl\qty(X\qty(\frac{i}{2^{n}})) \subset X\qty(\frac{i+1}{2^{n}}) \in \tau(X)$$
   であるから，cl-nhdより，$V \in \tau(\cl(X(i/2^{n})),X)$であって
   $$ \cl(V) \subset X\qty(\frac{i+1}{2^{n}})$$
   を満たすものが存在する．そこで
   $$ X(r) := V \in \tau(X)$$
   とおくと，
   $$ A_{0} \subset \cl\qty(X\qty(\frac{i}{2^{n}})) \subset X(r) \subset \cl(X(r)) \subset X\qty(\frac{i+1}{2^{n}}) \subset X \smallsetminus A_{1}$$
   が成り立つ．

改めて$X(1) := X$とおくと，$X$の開被覆$(X(r))_{r \in D}$はやはり
$$ r < s \implies \cl(X(r)) \subset X(s)$$
を満たすので，contiより，写像
$$ f := F_{(X(r))_{r\in D}} \colon X \to [0,1];\ x \mapsto \inf\{r \in D \mid x \in X(r)\}$$
は連続である．

1. $x \in A_{0}$のとき，$x \in A_{0} \subset X(0)$より
   $$ f(x) = 0$$
   が成り立つ．
2. $x \in A_{1}$のとき，
   $$ \{r \in D \mid x \in X(r)\} = \{1\}$$
   より
   $$ f(x) = 1$$
   が成り立つ．

$W \in \tau(C,X)$に対して，cl-nhdより，$C$の閉近傍$N_{1} \subset X$であって$N_{1} \subset W$を満たすものが存在する．ここで
$$ A' := \cl(A \smallsetminus N_{A \cap C}) = \cl(A \smallsetminus N_{A \cap C}) \cap A = \cl_{A}(A \smallsetminus N_{A \cap C})$$
とおくと，
$$ A' = \cl_{A}(A \smallsetminus N_{A \cap C}) = A \smallsetminus \I_{A}(N_{A \cap C}) \subset A \smallsetminus (A \cap C) = A \smallsetminus C$$
より，$A' \cap C = \varnothing$が成り立つ．したがって，$X \smallsetminus A' \in \tau(C,X)$に対して，cl-nhdより，$C$の閉近傍$N_{2} \subset X$であって$N_{2} \subset X \smallsetminus A'$を満たすものが存在する．この$N_{2}$について
$$ A \cap N_{2} \subset A \cap (X \smallsetminus A') = A \smallsetminus A' \subset N_{A \cap C}$$
が成り立つことに注意する．そこで$N_{0} := N_{1} \cap N_{2}$とおくと，
$$ C \subset \I(N_{1}) \cap \I(N_{2}) = \I(N_{1} \cap N_{2}) = \I(N_{0})$$
より$N_{0} \subset X$は$C$の閉近傍であり，
$$ N_{0} \subset N_{1} \subset W,$$
および
$$ A \cap N_{0} \subset A \cap N_{2} \subset N_{A \cap C}$$
が成り立つ．よって，
$$ N_{C} := N_{0} \cup N_{A \cap C}$$
とおくと，
$$ C \subset \I(N_{0}) \subset \I(N_{C})$$
より$N_{C} \subset X$は$C$の閉近傍であり，
$$ N_{C} \subset W \cup (A \cap W) \subset W,$$
および
$$ A \cap N_{C} = (A \cap N_{0}) \cup (A \cap N_{A \cap C}) = (A \cap N_{0}) \cup N_{A \cap C} = N_{A \cap C}$$
が成り立つ．

(i)$\implies$(ii)

$$ U \subset X \smallsetminus V \in \tau^{c}(X)$$
より
$$ \cl(U) \subset X \smallsetminus V \subset X \smallsetminus B,$$
すなわち
$$ \cl(U) \cap B = \varnothing$$
が成り立つ．

(ii)$\implies$(i)

$V := X \smallsetminus \cl(U)$とおけばよい．

任意の$n \in\mathbb{N}$に対して，
$$ F_{n} \cap \cl(C) \subset F \cap \cl(C) = \varnothing$$
と$X$の正規性より，$U_{n} \in \tau(F_{n},X)$であって
$$ \cl(U_{n}) \cap \cl(C) = \varnothing$$
を満たすものが存在する．同様に，任意の$m \in \mathbb{N}$に対して，
$$ \cl(F) \cap C_{m} \subset \cl(F) \cap C = \varnothing$$
と$X$の正規性より，$V_{m} \in \tau(C_{m},X)$であって
$$ \cl(F) \cap \cl(V_{m}) = \varnothing$$
を満たすものが存在する．そこで$X$の開集合$U,V \in \tau(X)$を
$$ U:= \bigcup_{n\in\mathbb{N}} \left(U_{n} \smallsetminus \bigcup_{j\in[n]} \cl(V_{j})\right),\ V:= \bigcup_{m\in\mathbb{N}} \left(V_{m} \smallsetminus \bigcup_{i\in[m]} \cl(U_{i})\right)$$
で定めると，任意の$n,m \in \mathbb{N}$に対して，
$$ F_{n} \subset U_{n} \cap \cl(F) \subset U_{n} \cap \left(X \smallsetminus \bigcup_{j\in[n]} \cl(V_{j})\right) = U_{n} \smallsetminus \bigcup_{j\in[n]} \cl(V_{j}),$$
および
$$ C_{m} \subset V_{m} \cap \cl(C) \subset V_{m} \cap \left(X \smallsetminus \bigcup_{i\in[m]} \cl(U_{i})\right) = V_{m} \smallsetminus \bigcup_{i\in[m]} \cl(U_{i})$$
が成り立つので，
$$ F = \bigcup_{n\in\mathbb{N}} F_{n} \subset U,\ C = \bigcup_{m\in\mathbb{N}} C_{m} \subset V$$
を得る．さらに，
$$ \left(U_{n} \smallsetminus \bigcup_{j\in[n]} \cl(V_{j})\right) \cap \left(V_{m} \smallsetminus \bigcup_{i\in[m]} \cl(U_{i})\right) = \left(U_{n} \smallsetminus \bigcup_{i\in[m]} \cl(U_{i})\right) \cap \left(V_{m} \smallsetminus \bigcup_{j\in[n]} \cl(V_{j})\right) = \varnothing $$
より，
$$ U \cap V = \varnothing$$
も成り立つ．

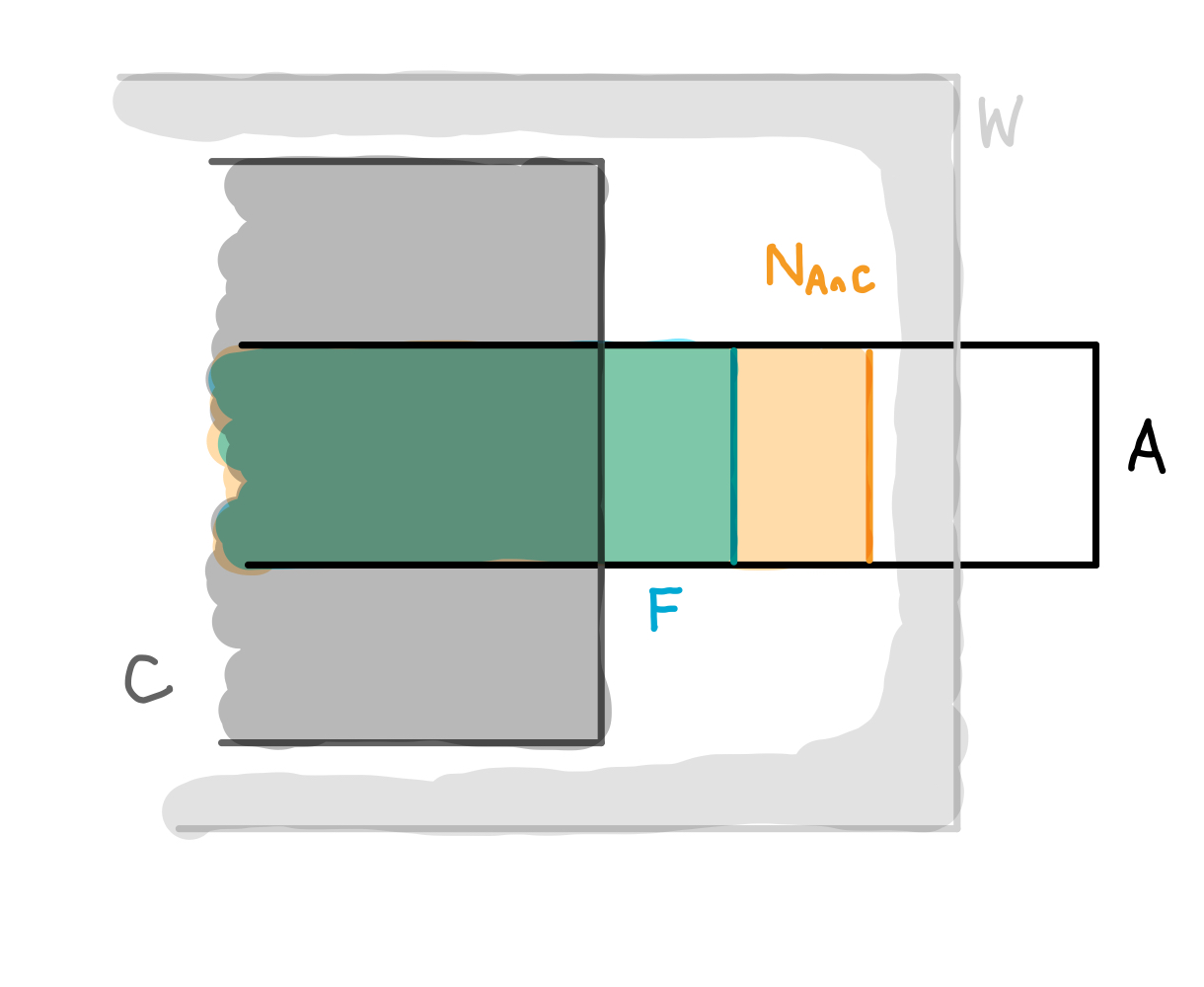
1. $F \in \tau(A)$より$N_{A\cap C} \subset A$は$A \cap C$の閉近傍なので，ossa-lemより，$C$の閉近傍$N'_{C} \subset X$であって
   $$ N'_{C} \subset W,\ A \cap N'_{C} = N_{A \cap C}$$
   を満たすものが存在する．
2. いま$A \subset X$が閉集合なので，$A$の閉集合の合併である$F, A \smallsetminus N_{A\cap C}$は$X$の$F_{\sigma}$集合で（も）ある．さらに$F \subset N_{A\cap C} \in \tau^{c}(X)$より
   $$ \cl(F) \subset N_{A\cap C} \subset W$$
   であるから，$X$の$F_{\sigma}$集合$F, (X \smallsetminus W) \cup (A \smallsetminus N_{A\cap C})$について，
   $$ F \cap \cl((X \smallsetminus W) \cup (A \smallsetminus N_{A\cap C})) = F \cap ((X \smallsetminus W) \cup \cl(A \smallsetminus N_{A \cap C})) = \varnothing,$$
   および
   $$ \cl(F) \cap ((X \smallsetminus W) \cup (A \smallsetminus N_{A\cap C})) = \varnothing$$
   が成り立つ．よって，F-sigma-separatedより，$F$の開近傍$V \in \tau(X)$であって
   $$ \cl(V) \cap ((X \smallsetminus W) \cup (A \smallsetminus N_{A\cap C})) = \varnothing$$
   を満たすものが存在する．このとき
   $$ \cl(V) \subset W,\ A \cap \cl(V) \subset N_{A\cap C}$$
   が成り立つことに注意する．
3. $N'_{C} \subset X$が$C$の閉近傍であったので，
   $$ N_{C} := N'_{C} \cup \cl(V) \subset X$$
   も$C$の閉近傍である．
   1. 明らかに$N_{C} \subset W$が成り立つ．
   2. $N'_{C},V$の取り方より
      $$ A \cap N_{C} = (A \cap N'_{C}) \cup(A \cap \cl(V)) = N_{A\cap C} \cup (A \cap \cl(V)) = N_{A\cap C}$$
      が成り立つ．
   3. $F \subset V \subset N_{C}$より
      $$ F \subset V \subset \I(N_{C})$$
      が成り立つ．