群作用の圏論的な記述
群の作用についての定義や記号については こちらの記事 のものを採用します.特に群の作用を$a_\rho\c G\times X\to X$と書いたら,対応する置換表現が$\rho\c G\to\mathfrak{S}(X)$であるとします.
群作用の圏論的な記述
まず群を圏論的に記述する.
群$G$に対して,圏$\mathscr{C}_G$が次のように定義される.
$$\Ob(\mathscr{C}_G)=\{*\}$$(つまり対象は1つだけ)
$$\Hom_{\mathscr{C}_G}(*,*)=G$$
恒等射は単位元$1$,射の合成は群の積.
群$G$はこの圏$\mathscr{C}_G$と同一視される.
群$G$の集合$X$への作用$a_\rho\colon G\times X\to X$を与えることは,関手$F_\rho\colon \mathscr{C}_G\to\Set$を与えることと等価である.
まず作用$a_\rho\colon G\times X\to X$が与えられたとき,
$$F_\rho(*)=X$$
として,$g\in G$に対し,
$$F_\rho(g)\coloneqq \rho(g)\colon X\to X$$
と定めれば$F_\rho\colon \mathscr{C}_G\to\Set$は関手になる.実際,作用の定義から,
$F_\rho(1)=\id_X,\ F_\rho(g\circ h)=F_\rho(g)\circ F_\rho(h)$
である.
一方,関手$F\colon \mathscr{C}_G\to\Set$が与えられたとき,準同型$\rho\colon G\to\mathfrak{S}(X)$を$\rho(g)\coloneqq F(g)$で定めることができる.関手性から
$$F(g)\in \mathfrak{S}(X),\ F(g\circ h)=F(g)\circ F(h)$$
が従う.
$a_\rho\colon G\times X\to X,a_\mu\colon G\times Y\to Y$を$G$作用とする.このとき,$G$同変写像$f\colon X\to Y$を与えることと,自然変換$\eta\colon F_\rho\too F_\mu$を与えることは等価である.
$G$同変$f\colon X\to Y$が与えられたとき,$\eta\colon F_\rho\too F_\mu$を
$$\eta_{*}=f\colon X(=F_\rho(*))\to Y(=F_\mu(*))$$
で定めれば$\eta$が自然変換である.実際,$G$同変の定義から
$$f\circ \rho(g)=\mu(g)\circ f$$
より
$$\eta_{*}\circ F_\rho(g)=F_\mu(g)\circ \eta_{*}$$
が成立することから従う.逆に自然変換から$G$同変も同様に構成できる.
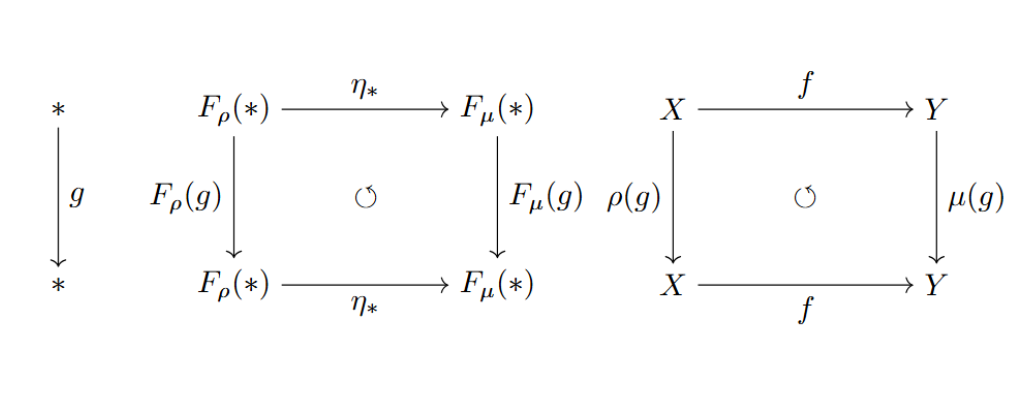 自然変換の図式
自然変換の図式
群$G$に対し$G$作用の圏$\Set^G$が
$$\Set^G\coloneqq\Set^{\mathscr{C}_G}=\Nat(\mathscr{C}_G,\Set)$$
で与えられる.対象は$G$作用,射は$G$同変写像である.
$F\in\Ob(\Set^G)$が$X=F(*)$であり,対応する置換表現が$\rho$であるとき,$F$を$(X,\rho)$とも表すことにする.
limitとcolimit
$F=(X,\rho)\in \Ob(\Set^G)$とする.このとき,
$$\lim_{\longleftarrow}F=X^G$$
つまり$F$のlimitは固定点集合である.
$(X^G,\iota\colon X^G\hookrightarrow X)$がlimitの普遍性を充たすことを示す.ここで$\iota$は包含である.まず$(X^G,\iota)$が錐であることを確認する.$g\in G,x\in X^G$に対し,$X^G$の定義から,
$$(F(g)\circ\iota)(x)=F(g)(x)=\rho(g)(x)=x=\iota(x)$$
よって,
$$\all g\in G,F(g)\circ\iota=\iota$$
である.また錐$(Y,j\colon Y\to X)$が与えられたとき,
$$\all g\in G, F(g)\circ j=j$$
より$j(Y)\subset X^G$である.よって$j$の終域を$X^G$に制限した写像$j'\colon Y\to X^G,y\mapsto j(y)$によって,
$$\iota\circ j'=j$$
とできる.このような$Y\to X^G$はこれ以外にあり得ず,uniqueである.
普遍性まで立ち返らなくても次のようにも分かる.$F$は$X$と$X$の間に射が複数あるような$\Set$上の図式であり,limitはequalizerである.よって,
\begin{align}
\lim_{\longleftarrow}F
&=\{x\in X |\all g\in G,F(g)(x)=\id_X(x)\}\\
&=\{x\in X |\all g\in G,\rho(g)(x)=x\}\\
&=X^G
\end{align}
$F=(X,\rho)\in \Ob(\Set^G)$とする.このとき,
$$\lim_{\longrightarrow}F=X/G$$
つまり$F$のcolimitは軌道空間である.
$(X/G,\pi\colon X\to X/G)$がcolimitの普遍性を充たすことを示す.ここで$\pi$は射影,つまり$\pi(x)\coloneqq \Orb_G(x)$とする.
まず$(X/G,\pi)$が余錐であることを確認する.$g\in G,x\in X$に対し,
$$(\pi\circ F(g))(x)=\pi(\rho(g)(x))=\Orb_G(\rho(g)(x))=\Orb_G(x)=\pi(x)$$
よって,
$$\all g\in G,\pi\circ F(g)=\pi$$
である.また余錐$(Y,q\colon X\to Y)$が与えられたとき,
$$\all g\in G,q\circ F(g)=q$$
である.ここで$x,y\in X$が同じ軌道上にあるとするとき,
$$\ex g\in G,y=\rho(g)(x)$$
であるから,
$$q(y)=q(\rho(g)(x))=(q\circ F(g))(x)=q(x)$$
である.よってwell-definedな写像
$$q'\colon X/G\to Y,\;\Orb_{G}(x)\mapsto q(x)$$
が誘導され,
$$q'\circ\pi=q$$
を充たす.このような$X/G\to Y$はこれ以外にあり得ず,uniqueである.
limitの場合と同様,普遍性に立ち返らずとも次のようにも分かる.$F$は$X$から$X$への射が複数ある図式であり,colimitはcoequalizerである.従って,
\begin{align}
R
&=\{(\id_X(x),F(g)(x))\in X^2\mid x\in X, g\in G\}\\
&=\{(x,\rho(g)(x))\in X^2\mid x\in X, g\in G\}
\end{align}
で生成される同値関係を$\sim$とすると$\sim=R$であり,これは同じ軌道上にいるという関係である.よって,
\begin{align}
\lim_{\longrightarrow}F=X/{\sim}=X/G
\end{align}
随伴1
$U\c \Set^G\to\Set$を
$$(X,\rho)\mapsto X,\ f\mapsto f$$
で定めると,これは関手であり,忘却関手という.但し射の対応は$G$同変写像を単なる写像と見做すということである.
忘却関手は作用の構造を忘れて台集合を返す関手である.
$\mathcal{F}\c \Set\to\Set^G$を
$$X\mapsto (G\times X,\rho),\ \rho(g)=L_g\times\id_X\;(g\in G)$$
$$f\mapsto \id_G\times f$$
で定めると,これは関手であり,自由関手という.但し,$L_g\c G\to G,\;h\mapsto gh$である.
$U\c \Set^G\to\Set$を忘却関手,$\mathcal{F}\c \Set\to\Set^G$を自由関手とする.このとき,$\mathcal{F}\dashv U$.
$X\in\Ob(\Set),(Y,\mu)\in\Ob(\Set^G)$に対し,
$$\Hom_{\Set^G}((G\times X,\rho),(Y,\mu))\cong\Hom_{\Set}(X,Y)$$
なる自然な同型がある.
$(\to)$$\eta\c (G\times X,\rho)\too(Y,\mu)$に対して,$\eta_*\c G\times X\to Y$が定まる.そこで$\eta_*(1,-)\c X\to Y$を対応させる.
$(\leftarrow)$$f\c X\to Y\ \text{in}\ \Set$に対して,
$$\eta_*\c G\times X\to Y,(g,x)\mapsto f(x)$$
なる$\eta\c (G\times X,\rho)\too(Y,\mu)$を対応させる.
以上の対応は互いに逆であり,$X,(Y,\mu)$ に関して自然である.
随伴2
$\Delta\c \Set\to\Set^G$を
$$X\mapsto (X,\rho),\ \rho(g)=\id_X\;(g\in G)$$
$$f\mapsto f$$
で定めると,これは関手であり,対角関手という.但し射の対応は任意の写像が$G$同変となることに基づく.
対角関手は集合に自明作用を対応させる関手である.
$(-)^G\c \Set^G\to\Set$を
$$(X,\rho)\mapsto X^G, f\mapsto f|_{X^G}$$
で定めると,これは関手であり,固定点関手ということにする.
固定点関手は作用を固定点集合を対応させる関手である.
$(-)/G\c \Set^G\to\Set$を
$$(X,\rho)\mapsto X/G,\ f\mapsto \overline{f}$$
で定めると,これは関手であり,軌道関手ということにする.但し,$\overline{f}$は$G$同型$f$が軌道空間に誘導する写像である.(
前の記事
命題2)
軌道関手は作用を軌道空間を対応させる関手である.
$\Delta\c \Set\to\Set^G$を対角関手,$(-)^G,(-)/G\c \Set^G\to\Set$をそれぞれ固定点関手,軌道関手とする.このとき,
$$(-)/G\dashv \Delta\dashv (-)^G$$
$(X,\rho)\in\Ob(\Set^G),Y\in\Ob(\Set)$ に対し,
$$\Hom_{\Set}(X/G,Y)\cong\Hom_{\Set^G}((X,\rho),\Delta Y)$$
なる自然な同型がある.
$(\to)$$f\colon X/G\to Y\ \text{in}\ \Set$が与えられたとき,
$$\eta_*\coloneqq f\circ\pi\colon X\to Y $$
とおく.$x\in X,g\in G$に対し
$$\eta_*(\rho(g)(x))
=(f\circ\pi)(\rho(g)(x))
=(f\circ\pi)(x)
=\eta_*(x)$$
より,$\eta_*$は$G$同変である.従って$\eta\colon (X,\rho)\too\Delta Y$が得られる.
$(\leftarrow)$$\eta\colon (X,\rho)\too\Delta Y$とする.$x,y\in X$が同じ軌道にあるとき,
$$\exists g\in G,\ y=\rho(g)(x)$$
であるからして,
$$\eta_*(y)=\eta_*(\rho(g)(x))=\eta_*(x)$$
が成り立つ.よってwell-definedな写像
$$f\colon X/G\to Y,\ f(\Orb_G(x))\coloneqq \eta_*(x)$$
が定まる.
以上の対応は互いに逆であり,$(X,\rho),Y$ に関して自然である.
$X\in\Ob(\Set),(Y,\rho)\in\Ob(\Set^G)$に対し,
$$\Hom_{\Set^G}(\Delta X,(Y,\rho))\cong\Hom_{\Set}(X, Y^G)$$
なる自然な同型がある.
$(\to)$$\eta\colon \Delta X\too(Y,\rho)$とする.$x\in X,g\in G$に対し,
$$\rho(g)(\eta_*(x))=\eta_*(\id_X(x))=\eta_*(x)$$
が成り立つので$\eta_*(X)\subset Y^G$である.よって$\eta_*$の終域を$Y^G$に制限することで,
$$f\colon X\to Y^G,\ x\mapsto \eta_*(x)$$
が定まる.
$(\leftarrow)$$f\colon X\to Y^G\ \text{in}\ \Set$が与えられたとき,包含$\iota\colon Y^G\hookrightarrow Y$を用いて,
$$\eta_*\coloneqq \iota\circ f\colon X\to Y$$
と定める.このとき$g\in G$に対して,
$$\rho(g)(\eta_*(x))=\rho(g)(f(x))=f(x)=\eta_*(x)$$
であるからして$\eta_*$は$G$同変であり,
$$\eta\colon \Delta X\too(Y,\rho)$$
を与える.
以上の対応は互いに逆であり,$X,(Y,\rho)$ に関して自然である.
命題3から$\dps\lim_{\longleftarrow}=(-)^G$,命題4から$\dps\lim_{\longrightarrow}=(-)/G$となること及び$$\lim_{\longrightarrow}\dashv \Delta\dashv \lim_{\longleftarrow}$$
という事実からも従うことがわかる.
終わり
もし誤謬などありましたら教えて頂けると助かります.
