x^4+y^4=1の第1象限の積分
はじめに
ご機嫌よう!りーるるです.
最近留数定理との再会を果たし,楽しんでいる人です.
前回の記事(拡張された留数定理)は完全なものにしてからまたあげます.
突然ですが
$x^2+y^2=1$で表せられる曲線はなんですか?
もちろん、円ですよね.では、
$$x^4+y^4=1$$
が描く図形はどうなると思いますか?
正解はこちらです!
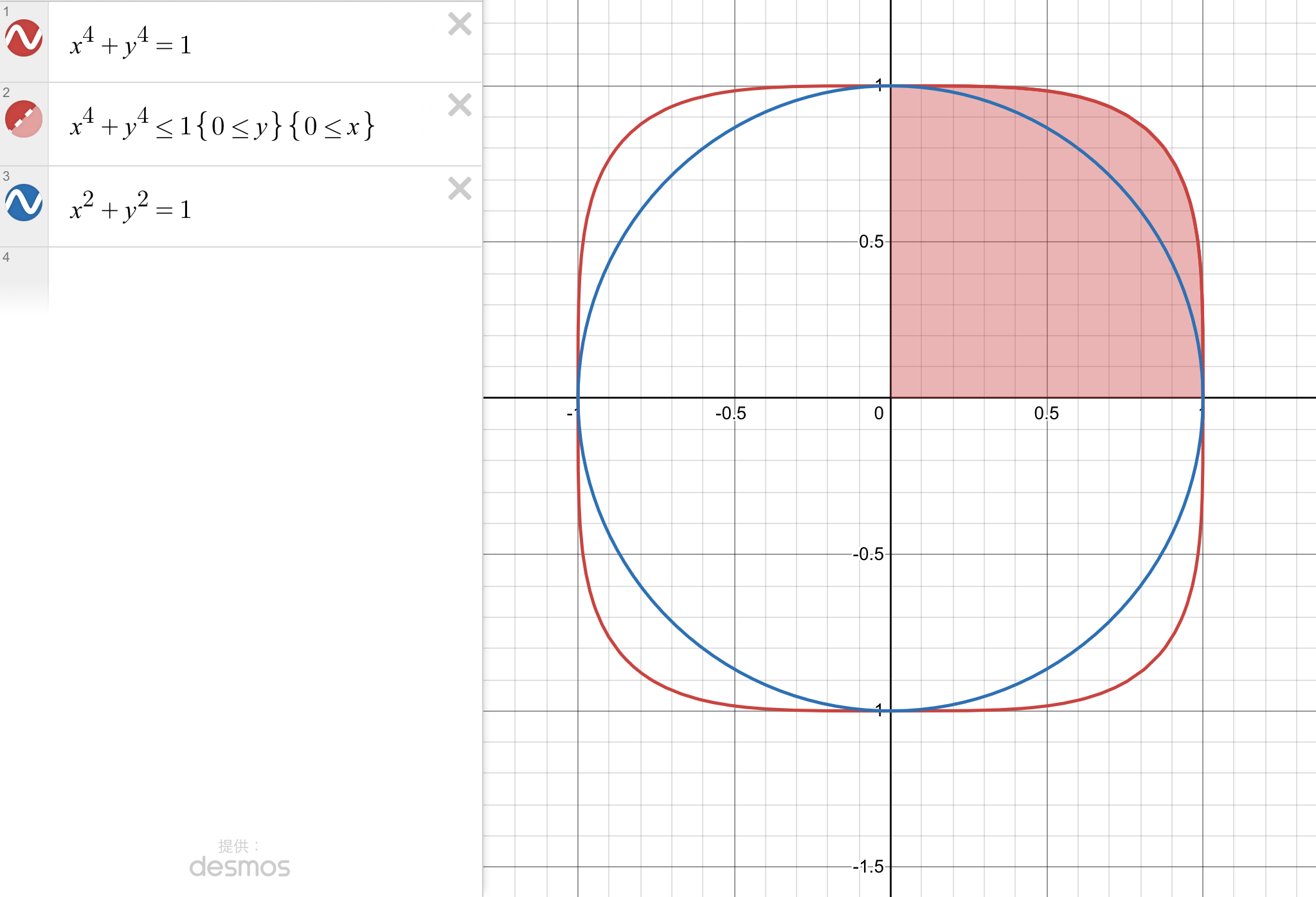
今回はこの薄い赤の部分の面積を求めます.式としては
$$y^4=1-x^4$$
$$y=\sqrt[4]{1-x^4}$$ですね!
てことで今回の問題です.
次の定積分を解け.
$$\int_0^1\sqrt[4]{1-x^4}dx$$
ガンマ関数,ベータ関数が出てきます.
本題
次の定積分を解け.
$$\int_0^1\sqrt[4]{1-x^4}dx$$
$$I=\int_0^1\sqrt[4]{1-x^4}dx$$
とする.
$x^4=t$と置換すると,
$$I=\int_{0}^{1}\dfrac{1}{4}t^{-\frac{3}{4}}(1-t)^{\frac{1}{4}}dt=\dfrac{1}{4}\int_{0}^{1}t^{-\frac{3}{4}}(1-t)^{\frac{1}{4}}dt$$ $\;$
これはベータ関数を用いて$\dfrac{1}{4}B\biggl(\dfrac{1}{4},\dfrac{5}{4}\biggl)$と表せる.
$B(x,y)=\dfrac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$であるから
$$I=\dfrac{1}{4}B\biggl(\dfrac{1}{4},\dfrac{5}{4}\biggl)=\dfrac{1}{4}\dfrac{\Gamma\biggl(\dfrac{1}{4}\biggl)\Gamma\biggl(\dfrac{5}{4}\biggl)}{\Gamma\biggl(\dfrac{3}{2}\biggl)}$$
$\Gamma\biggl(\dfrac{3}{2}\biggl)=\dfrac{\sqrt{\pi}}{2}$より,
$$I=\dfrac{1}{2\sqrt{\pi}}\Gamma\biggl(\dfrac{1}{4}\biggl)\Gamma\biggl(\dfrac{5}{4}\biggl)$$
$\Gamma(x)\Gamma(1-x)=\dfrac{\pi}{\sin{\pi x}}$より,$x=\dfrac{5}{4}$のとき,
$$\Gamma\biggl(\dfrac{5}{4}\biggl)\Gamma\biggl(-\dfrac{1}{4}\biggl)=\dfrac{\pi}{\sin{\dfrac{5\pi}{4}}}=-\sqrt{2}\pi$$
$$ \Gamma\biggl(\dfrac{5}{4}\biggl)=-\dfrac{\sqrt{2}\pi}{\Gamma\biggl(-\dfrac{1}{4}\biggl)}$$
これを先ほどの式に代入すると
$$ I=\dfrac{1}{2\sqrt{\pi}}\Gamma\biggl(\dfrac{1}{4}\biggl)\Gamma\biggl(\dfrac{5}{4}\biggl)=-\dfrac{1}{2\sqrt{\pi}}\Gamma\biggl(\dfrac{1}{4}\biggl)\dfrac{\sqrt{2}\pi}{\Gamma\biggl(-\dfrac{1}{4}\biggl)}$$
これを整理すると.
$$I=-\sqrt{\dfrac{\pi}{2}}\dfrac{{\Gamma\bigl(\frac{1}{4}\bigl)}}{{\Gamma\bigl(-\frac{1}{4}\bigl)}}$$
となり題意を得る.
数値としては$0.927037\cdots$です.
$ \dfrac{1}{4}$の円が$\dfrac{\pi}{4}$で$0.785398\cdots$です.
だいぶ変わるもんですね!
これと同様に$$x^a+y^b=1$$もできますのでぜひ.
ではまた!
