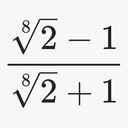素数ゼータ関数
定義
| $\delta_{a,b}$ | クロネッカーのデルタ |
| $\displaystyle \sum_p, \prod_p$ | 素数を小さい順に演算 |
| $\displaystyle L(s,f) \coloneqq \sum_{n=1}^\infty f(n)n^{-s}$ | L関数 |
| $\beginend{align}{ P(s) \acoloneqq \sum_pp^{-s} \\ P(s,f) \acoloneqq \sum_pf(p)p^{-s} }$ | 素数ゼータ関数 |
| 自然数を定義域として かつ$\alpha(1)\ne0$である 関数$\alpha$に対して$\alpha^{-1}$を $\displaystyle \sum _{d\mid n} \alpha(d)\alpha^{-1}\lr({\frac nd}) = \delta_{n,1} $ とする。 | ディリクレ逆元 |
通常の素数ゼータ関数
特殊関数 グラフィックスライブラリー
に複素関数としての考察やグラフがあります。
本記事における$P^{(n)}(0)$に関する考察は独自に考えた厳密ではないもののため留意してください。
補題
$\displaystyle \sum _{d|n} \mu(d) = \delta_{n,1}$
$\displaystyle x\ge1$
$\beginend{align}{
g(x) &= \sum _{{n=1}}^\infty \alpha(n){f(nx)}{n^{-s}} \\ \Longleftrightarrow
f(x) &= \sum _{{n=1}}^\infty \alpha^{-1}(n){g(nx)}{n^{-s}}
}$
メビウスの反転公式(Wikipedia) と呼ばれるものの一つです。
$\qquot\Longleftrightarrow$の両辺が対称的であるため、$\qquot\Longrightarrow
$のみ証明する。
$\beginend{align}{
\sum _{{n=1}}^\infty \alpha^{-1}(n){g(nx)}{n^{-s}} &=
\sum _{{n=1}}^\infty \alpha^{-1}(n){n^{-s}}
\sum _{{k=1}}^\infty \alpha(k){f(nkx)}{k^{-s}} =
\sum _{{l=1}}^\infty {f(lx)}{l^{-s}} \sum _{k|l} \alpha(k)\alpha^{-1}\lr({\frac lk}) \\&=
\sum _{{l=1}}^\infty {f(lx)}{l^{-s}}\delta_{l,1} =
f(x) \\
}$
$\displaystyle x\ge1$
$\beginend{align}{
g(x) &= \sum _{{n=1}}^\infty {f(nx)}{n^{-s}} \\ \Longleftrightarrow
f(x) &= \sum _{{n=1}}^\infty \mu(n){g(nx)}{n^{-s}}
}$
補題1より$\alpha(n)=1$に対して$\alpha^{-1}(n)=\mu(n)$であるため、これを補題2に代入する。
リーマンゼータ関数
$\beginend{align}{ \ln\zeta(s) &= \sum_{n=1}^\infty \frac{P(ns)}n \\ P(s) &= \sum_{n=1}^\infty \frac{\mu(n)}n\ln\zeta(ns) }$
より。
高さは絶対値、色は偏角を表します。](https://math-functions-1.watson.jp/gazou_spec030/030_0630.png)
特殊関数 グラフィックスライブラリー より。
高さは絶対値、色は偏角を表します。
$\beginend{align}{ \ln\zeta(s) &= \ln\prod_p\frac1{1-p^{-s}} = -\sum_p \ln\!\lr({1-p^{-s}}) \\&= \sum_p \sum_{n=1}^\infty\frac{p^{-ns}}n = \sum_{n=1}^\infty \frac{P(ns)}n \\ \asupplement{-25pt}{補題3より、} \\ P(s) &= \sum_{n=1}^\infty \frac{\mu(n)}n\ln\zeta(ns) }$
この式から、$s=1$に対数分岐点があり、$\displaystyle P(0) =
\ln\zeta(0)\sum_{n=1}^\infty \frac{\mu(n)}n =
\frac{\ln\!\lr({-\frac12})}{\zeta(1)} = 0$
であることが推測できます。
複素平面上でグラフにしてみると、虚軸付近に対数分岐点が密集していることが伺えます。
特殊値
$n\in2\N_0\cup\{1\}$
$P^{(n)}(0) = \dfrac{(-1)^{n+1}n}{B_n}\lr.{(\ln\zeta(s))^{(n)}}|_{s=0}$
上述した$P(0)=0$の一般化です。厳密な証明ではないため、予想というべきかもしれません。
$\beginend{align}{ \asupplement{-60pt}{定理1より、} \\ \ln\zeta(s) &= \sum_{k=1}^\infty \frac{P(ks)}k \\ \asupplement{-60pt}{$n$階微分して$s=0$を代入し、} \\ \lr.{(\ln\zeta(s))^{(n)}}|_{s=0} \qquot{&=} P^{(n)}(0)\sum_{k=1}^\infty k^{n-1} \\&= P^{(n)}(0)\zeta(-n+1) \\&= \frac{(-1)^{n+1}B_n}nP^{(n)}(0) }$
冪級数展開
任意の$n\in2\N_0+1$で$\lr.{\lr({\dfrac{\zeta'(s)}{\zeta(s)}})^{(n)}}|_{s=0}$が有限の値として定義され、定理2を認めるならば、
$P(s)$の偶成分$\dfrac{P(s)+P(-s)}2$を$s=0
$でテイラー展開できます。
$\displaystyle \frac{P(s)+P(-s)}2 = -\sum_{n=1}^\infty \frac{s^{2n}}{(2n-1)!B_{2n}} \lr.{\lr({\frac{\zeta'(t)}{\zeta(t)}})^{(2n-1)}}|_{t=0}$
定理2より、
$\displaystyle \sahen = \sum_{n=0}^\infty \frac{P^{(2n)}(0)}{(2n)!}s^{2n} = \uhen$
$\displaystyle \sum_{n=1}^\infty \frac{s^{2n-1}}{(2n-1)!}
\lr.{\lr({\frac{\zeta'(t)}{\zeta(t)}})^{(2n-1)}}|_{t=0} =
\frac12\lr({\frac{\zeta'(t)}{\zeta(t)}-\frac{\zeta'(-t)}{\zeta(-t)}})$
の収束半径が$0$でなければ、上記の冪級数の収束半径は$\infty$となり$\dfrac{P(s)+P(-s)}2$は整関数となります。
その場合、$P(s)$の特異点は全て奇成分$\dfrac{P(s)-P(-s)}2$に由来することになります。
ディリクレ指標による一般化
ディリクレ指標
$\chi_0$は法$N$の自明な指標。
補題
$\displaystyle x\ge1$
$\beginend{align}{
g(x) &= \sum _{{n=0}}^\infty {f((2n+1)x)}{(2n+1)^{-s}} \\ \Longleftrightarrow
f(x) &= \sum _{{n=0}}^\infty \mu(2n+1){g((2n+1)x)}{(2n+1)^{-s}}
}$
$\alpha(n)=\beginend{cases}{
0 &\mathrm{if}\ 2\mid n \\
1 &\mathrm{if}\ 2\nmid n
}$
に対して、
$\alpha^{-1}(n)=\beginend{cases}{
0 &\mathrm{if}\ 2\mid n \\
\mu(n) &\mathrm{if}\ 2\nmid n
}$
とすれば、$\displaystyle \sum _{d\mid n} \alpha(d)\alpha^{-1}\lr({\frac nd}) = \delta_{n,1}
$が成り立つ。
$n$が偶数の時、$d$と$\dfrac nd$の少なくとも一方が偶数となるため
$\displaystyle \sum _{d|n} \alpha(d)\alpha^{-1}\lr({\frac nd}) = 0
$となり、
$n$が奇数の時、$d$と$\dfrac nd$の両方が奇数となるため、補題1より
$\displaystyle \sum _{d|n} \alpha(d)\alpha^{-1}\lr({\frac nd}) = \delta_{n,1}
$となる。
$\displaystyle L(s,\chi_0) = \qty[\prod_{p|N} \lr({1-p^{-s}})]\zeta(s)$
L関数
$\chi$は法$N$の実指標。
$\beginend{align}{
\ln L(s,\chi) &= \sum_{n=0}^\infty \frac{P((2n+1)s,\chi)}{2n+1} +
\frac12\lr({\ln\zeta(2s)+\sum_{p|N} \ln\!\lr({1-p^{-2s}})}) \\
P(s,\chi) &= \sum_{n=0}^\infty \frac{\mu(2n+1)}{2n+1}\lr[{
\ln L((2n+1)s,\chi)-\frac12\lr({
\ln\zeta((4n+2)s)+\sum_{p|N} \ln\!\lr({1-p^{-(4n+2)s}})})}]
}$
$\beginend{align}{ \ln L(s,\chi) &= \ln\prod_p\frac1{1-\chi(p)p^{-s}} = -\sum_p \ln\!\lr({1-\chi(p)p^{-s}}) = \sum_p \sum_{n=1}^\infty \frac{\chi(p)^np^{-ns}}n \\&= \sum_p \sum_{n=1}^\infty \lr({ \frac{\chi(p)p^{-(2n-1)s}}{2n-1} + \frac{\chi_0(p)p^{-2ns}}{2n}}) \quad{\small\pmatrix{ \textsf{$\chi(k)\in\{0,1,-1\}\land|\chi(k)|=\chi_0(k)$であるため、} \\ \textsf{$\chi(k)^{2n-1}=\chi(k),\chi(k)^{2n}=\chi_0(k)$。} }} \\&= \sum_{n=0}^\infty \frac{P((2n+1)s,\chi)}{2n+1} + \frac{\ln L(2s,\chi_0)}2 \\&= \sum_{n=0}^\infty \frac{P((2n+1)s,\chi)}{2n+1} + \frac12\lr({\ln\zeta(2s)+\sum_{p|N} \ln\!\lr({1-p^{-2s}})}) \\ \asupplement{-35pt}{補題4より、} \\ P(s,\chi) &= \sum_{n=0}^\infty \frac{\mu(2n+1)}{2n+1}\lr[{ \ln L((2n+1)s,\chi)-\frac12\lr({ \ln\zeta((4n+2)s)+\sum_{p|N} \ln\!\lr({1-p^{-(4n+2)s}})})}] }$
$\chi$が自明な指標である場合、定理1に帰着されます。
定理2と同様にして、
$\displaystyle P^{(n)}(0,\chi) = \frac{(-1)^{n+1}n}{\lr({1-2^{n-1}})B_n}
\lr.{\lr[{\ln L(s,\chi)-\frac12\lr({\ln\zeta(2s)+\sum_{p|N} \ln\!\lr({1-p^{-2s}})})}]^{(n)}}|_{s=0}$
という式が導けます。しかし、$N\ge2$の時一般に$\displaystyle \sum_{p|N} \ln\!\lr({1-p^{-2s}})$やその$n$階導関数は$s=0$に特異点を持つため$P^{(n)}(0,\chi)$を定義するのは困難です。