位相とは収束関係（開集合アンチのための位相空間の定義）
はじめに
はじめまして。私は推しの記事をきっかけにMathlogを使ってみることにしたMathlog初心者。一部オリジナルな定義や冗長な日本語を使っているが、大目に見てほしい。
本文
邪道へようこそ
多くの位相空間論の入門書では、位相を開集合系として定義している。この定義を初めて見たとき、どう感じただろうか？「距離空間の拡張として開集合だけを考えればいい！」のような説明の後に、中途半端な集合演算について閉じてる謎の部分集合族が与えられて、「公理は開区間の性質の一般化だよ」と言われても飛躍がありすぎると思わなかったか？連続写像も「位相構造を保つ写像」らしいけれど、群の準同型やベクトル空間の線形写像と違って逆像で定義されていて、なんだか構造(？)を保ってる感が無い。第一、集合に入れてる構造が何なのか、公理の意味は何かがイメージしづらい。これは、具体から抽象に向かって定義しようとするから、飛躍を感じてもやもやするのだ。そこで、同値な定義に言い換えるとイメージがはっきりする。答えを言うと、集合に入れている構造は点族の収束という多項関係たちである。
集合$X$で、どの点族がどの点に収束するか決めた関係$ \rightarrow $を収束関係と呼ぶ。位相空間とは、集合に収束関係を入れた構造$(X,\rightarrow)$のうち,いくつかの公理を満たすものに他ならない。そして連続写像とは、この関係構造の準同型写像のことをいう。
収束論の一歩目￤ネットと収束関係
一般の「収束」を表現するには？
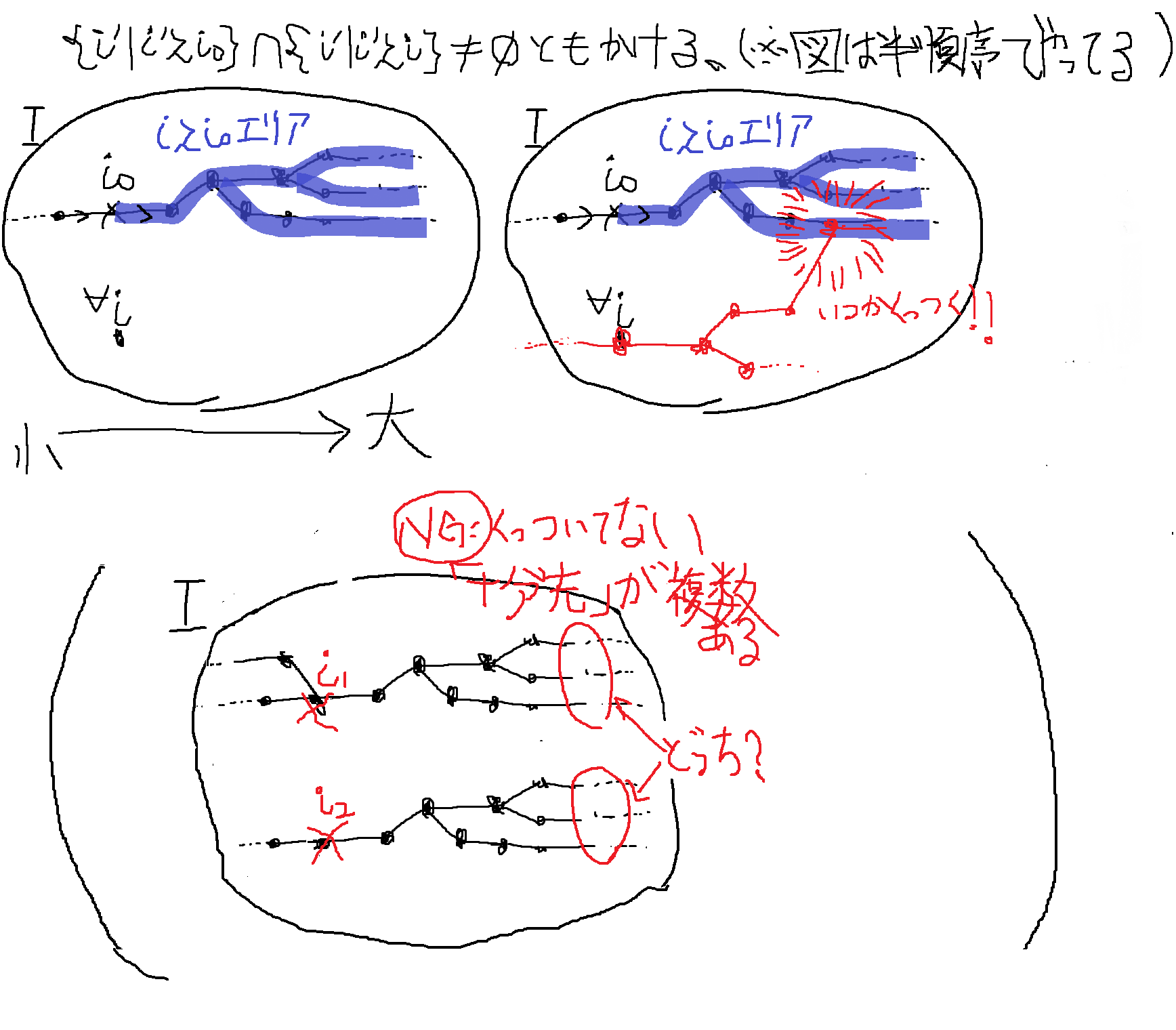
そもそも、「収束」を表現するには何が必要だろうか？距離空間では、点列の収束だけで関数の収束を定義できた。だが、点列のままではラベル(＝添字)の可算性や全順序性という強い束縛を受けるため、一般の収束っぽい概念を表現するには不十分だ。例えば、リーマン積分の定義に出てくる謎極限は点列で表現できない。（リーマン積分の定義は例2で触れる）。点列だけではこういう収束を表現できない。そこで、非可算個のラベルも認めることにする。点列$(x_n)_{n \in \mathbb{N} }$ではなく、より一般の点族$(x_i)_{i\in I}$を使おう。収束とは「点を選んでいって十分先でどの点に集まるか？」の情報というイメージがある。このままではただ点を$I$個選んだだけで、どの順番で選んだか、「十分先」がどちらか分からない。なので、ラベル$I$に順序を入れる。ここでは弱めに前順序$\lesssim_I$を入れることにする。さらに、上に有向という仮定を追加する。ざっくりいうと「十分先」が１方向だけしかないという意味だ。
明らかに、全順序は有向前順序。半順序は有向前順序とは限らない。
☆ 上に有向とは？ ☆
上に有向の個人的なイメージを図1に載せる（※図は半順序としている）。上に有向とは\begin{equation}
(\forall i_0,i\in I)[\{i'\mid i'\gtrsim_I i_0\}\cap\{i'\mid i'\gtrsim_I i\}\neq \varnothing ]
\end{equation}
と言い直せる。
\begin{equation}
\lnot (\exists i_1,i_2\in I)[\{i'\mid i'\gtrsim_I i_1\}\cap\{i'\mid i'\gtrsim_I i_2\}= \varnothing ]
\end{equation}
とも言い直せるね。要は、「十分先」が２パターン以上解釈できるケースを排除する制約なのだ。
上に有向の個人的イメージ図（この落書きを図と言い張る勇気）
$X$を集合とする(空でもよい)。非空有向前順序集合$(I,\lesssim_I)$と、$I$から$X$への写像$(x_i)_{i\in I}$の組$((I,\lesssim_I),(x_i)_{i\in I})$を$X$上のネット（有向点族）と呼ぶ。$X$上のネット全体を$\text{Net}(X)\coloneqq\coprod_{(I,\lesssim_I)\in DS}X^I$とかく*0。ラベル集合$(I,\lesssim_I)$が明らかな場合、点族$(x_i)_{i\in I}$をネットということもある。
ラベルに入ってる順序が違えば、関数として同じ点族も区別する。
点列とは、ラベルが$(\mathbb{N},\leq)$のネットのことである。
非空有向前順序集合$(I,\lesssim_I)$に対して、$I+1$項関係$\rightarrow_{(I,\lesssim_I)} \subseteq X^I \times X$を$(I,\lesssim_I)$-ネットの収束関係という。各$(I,\lesssim_I)\in DS$ごとに$(I,\lesssim_I)$-ネットの収束関係を１つずつ選んだ組$(\rightarrow_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS}$をネットの収束関係という。ネットの収束関係を付加した関係構造$(X,( \rightarrow_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS})$を（なんと言おう？）
$\rightarrow_{(I,\lesssim_I)}$は演算ではなく関係なので、収束点の個数に制約はない。なので、どの点にも収束しないネットがあっていいし、複数の異なる点に収束するネットがあってもいい。
もちろん$(\rightarrow_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS}$は$\text{Net}(X)\times X$の部分集合とも思える*1。そう思う場合は、単に$\rightarrow$と書くことにする。
収束関係を保つ写像を連続写像という。順序関係に対する単調写像と同じようなものだ。
関係構造$(X,( \rightarrow_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS})$の準同型写像を連続写像という。つまり$(X,( \rightarrow_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS})$と$(Y,( \rightarrow'_{(I,\lesssim_I)})_{(I,\lesssim_I)\in DS})$の間の写像$f:X\rightarrow Y $が連続であるとは
を満たすこと。
さて、このままネットで話を進めることもできるが、以下２つの理由で少しやりにくい。
- ラベルが非空有向前順序集合全体$DS$を走っているが、$\textsf{ZFC}$でこれは集合にならない。$\text{Net}(X)$が$\text{ill-defined}$になるため、$\textsf{NBG}$などのクラスを扱える集合論の公理系に乗り換える必要がある。
- このあと公理を追加するが、そのいくつかで部分ネットを使わなければならない。ネットの部分ネット全てを調べるのが地味に大変。
ちょっと適当に言うと、ネットは無駄に表現力が高くて計算しにくい。そのため、真フィルターという概念を使って定義を言い換える。
真フィルターによる収束関係の言い換え
集合$X$の部分集合族$\mathcal{F}\subseteq\mathcal{P}(X)$が真フィルターであるとは
を満たすこと。
- (1),(2)を満たすとき「フィルター基」、(1),(2),(3)を満たすとき「フィルター」という。(4)も満たすとき「真」をつける。
- (3)を仮定すると、(1)は$X\in \mathcal{F}$と、(2)は$A,B\in \mathcal{F} \Longrightarrow A \cap B\in\mathcal{F}$と同値になる。
- $\left\uparrow\, \mathcal{A}\right.\coloneqq \{S\subseteq X\mid(\exists A\in \mathcal{A})[A\subseteq S]\}$を上に閉じさせる閉包という。これは$\mathcal{A}$を含む最小の上に閉じた集合族になる。フィルターは上に閉なので、$\uparrow\mathcal{F}=\mathcal{F}$。$\mathcal{B}$がフィルター基であることと、$\uparrow\mathcal{B}$がフィルターであることは必要十分。真フィルター$\mathcal{F}$に対して、$\mathcal{F}=\left\uparrow\mathcal{B}\right.$となる$\mathcal{B}$を$\mathcal{F}$の真フィルター基という。定義を書き換えると、\begin{equation} S\in\mathcal{F}\Longleftrightarrow (\exists B\in\mathcal{B})[B\subseteq S]\end{equation}になる.（この変形は地味に頻出）。$\left\uparrow( \cdot ):\mathcal{P}(X)\rightarrow\mathcal{P}(X)\right.;$は閉包作用素の性質：$\mathcal{A}\subseteq \left\uparrow\,\mathcal{B}\right. \Longleftrightarrow \left\uparrow\,\mathcal{A}\right. \subseteq \left\uparrow\,\mathcal{B}\right.$を満たす。ちなみに、閉包作用素の一般論はこの子$[4]$の記事が詳しい。
これらの性質を確かめてみよう！
$X$の真フィルター全体を$\Phi(X)$と書く。これは$\textsf{ZFC}$でも集合になる。$(\Phi(X),\subseteq)$の極大元を極大真フィルター（またはウルトラ☆フィルター、うると..etc）という。$X$の極大真フィルター全体を$\text{Ult}(X)$と書く。
ネット$((I,\lesssim_I),(x_i)_{i\in I})$に対して、
\begin{eqnarray*}
\mathcal{E}_{((I,\lesssim_I),(x_i)_{i\in I})}&\coloneqq&\{A\subseteq X\mid(\exists i_0\in I)(\forall i\in I)[i\gtrsim_I i_0 \Longrightarrow x_i\in A]\} \\
&=& \left\uparrow\{\{x_i\mid i\gtrsim_I i_0\} \mid i_0\in I\}\right.
\end{eqnarray*}
は真フィルターになる。確かめてみよう！$ \{\{x_i\mid i\gtrsim_I i_0\} \mid i_0\in I\}$が真フィルター基になることを見れば十分。これをeventuallyフィルターという。
eventuallyフィルターをひとことで言うと、十分先で全部含む集合の一覧のこと。
ネットにeventuallyフィルターを対応させる写像
$\mathcal{E}_{\bullet}:\text{Net}(X)\longrightarrow \Phi(X)$は全射
真フィルター基$\mathcal{B}$に対して
\begin{eqnarray}
\left\{
\begin{array}{l}
I\coloneqq\{(x,S)\in X\times\mathcal{B}\mid x\in S\}, \\
(x,S)\lesssim_I(y,S'):\Longleftrightarrow S\supseteq S'
\end{array}
\right.
\end{eqnarray}
と定義すると$(I,\lesssim_I)$は非空有向前順序集合になり、さらに
\begin{array}{rccc}
n\colon &I &\longrightarrow& X \\ & (x,S) & \longmapsto & n(x,S)\coloneqq x;
\end{array}
とすると
\begin{equation}
\{\{n(x,S)\mid (x,S)\textcolor{red}{\gtrsim_I} (x_0,S_0)\} \mid (x_0,S_0)\in I\}=\mathcal{B}
\end{equation}
となる。確かめてみよう。特に、真フィルターは自身の真フィルター基なので、eventuallyフィルターの定義から$\mathcal{E}_{((I,\lesssim_I),n)}=\mathcal{F}$を得る。
（※$X= \varnothing$のときは$\text{Net}(\varnothing)=\Phi(\varnothing)=\varnothing$なので空虚な真）
上の写像$\mathcal{E}_\bullet$から誘導される同値関係をTail同値と呼び、$ \sim_{\text{Tail}} $と表記する。
$(x_i)_{i\in I}\sim_{\text{Tail}}(y_j)_{j\in J}\; :\Longleftrightarrow\;\mathcal{E}_{(x_i)_{i\in I}}=\mathcal{E}_{(y_j)_{j\in J}}$
適当にいうと十分先の挙動が同じになること。なお、以降は定義7のようにネットのラベル集合を省略して書く。ネットの収束関係も、以降は$\text{Net}(X)\times X$の部分集合だと思って$\rightarrow$と書くことにする。
$\text{Net}(X)/{\sim_{\text{Tail}}}\overset{\mathcal{E}_\bullet}{\cong} \Phi(X)$
$\Phi(X)\times X$の部分集合を真フィルターの収束関係という。
真フィルターの収束関係は、ネットの収束関係のうちTail同値なネットの収束が区別できないという公理
\begin{equation}
\bigcirc\, (x_i)_{i\in I}\sim_{\text{Tail}}(y_j)_{j\in J} \Longrightarrow (\forall \alpha\in X)[(x_i)_{i\in I}\rightarrow \alpha \Longleftrightarrow (y_j)_{j\in J}\rightarrow \alpha]
\end{equation}
を満たすものと同一視できることが、系1から直ちに分かる*2。eventuallyフィルターによって(Tail同値な)ネットと真フィルターが対応している。さて、この公理〇は「収束は十分先の挙動だけで決まる」、「手前のほうでどう選んだかは無関係」という意味だが、なんだか収束っぽいね。というよりも、私たちが"収束"と呼ぶ具体的な概念のほとんどが、この公理〇を満たしていそうだ。
真フィルターというのはただ$\text{Net}(X)/{\sim_\text{Tail}}$の別表現を与えているだけで、本質はTail同値という潰し方自体にある。
次に、位相を定義するための準備として部分ネットを定義する。
$(y_j)_{j\in J}$は$(x_i)_{i\in I}$の部分ネットである $: \Longleftrightarrow\:\, \mathcal{E}_{(x_i)_{i\in I}}\subseteq\mathcal{E}_{(y_j)_{j\in J}}$
以下の概念はTail同値の違いを除いて同じ。（つまり任意の片方に対して、Tail同値なもう片方が存在する。）
- $(x_i)_{i\in I}$の部分ネット
- $(x_i)_{i\in I}$に、ある共終写像*3$\phi:J\rightarrow I$を合成したネット$(x_{\phi(j)})_{j\in J}$
- $(x_i)_{i\in I}$に、ある単調な共終写像$\phi:J\rightarrow I$を合成したネット$(x_{\phi(j)})_{j\in J}$
$(x_i)_{i\in I}$の部分ネットを$(y_j)_{j\in J}$とおく。
\begin{eqnarray}
\left\{
\begin{array}{l}
K\coloneqq \{(i,j)\in I\times J\mid x_i=y_j\}, \\
(i,j)\lesssim_K (i',j') :\Longleftrightarrow(i\lesssim_I i',j\lesssim_J j'),
\end{array}
\right.
\end{eqnarray}
\begin{array}{rccc}
\phi\colon &K &\longrightarrow& I \\ & (i,j) & \longmapsto & \phi(i,j)\coloneqq i;
\end{array}
とすれば、一番目からTail同値な三番目が作れる。$\mathcal{E}_{(x_{\phi(i,j)})_{(i,j)\in K}}\subseteq \mathcal{E}_{(y_j)_{j\in J}}$は$(y_j)_{j\in J}$が部分ネットである仮定から、$\mathcal{E}_{(x_{\phi(i,j)})_{(i,j)\in K}}\supseteq \mathcal{E}_{(y_j)_{j\in J}}$は部分ネットの仮定と$J$が上に有向なことから言える。また明らかに、三番目$\subseteq$二番目$\subseteq$一番目。$\mathcal{F}\in\Phi(X)$のとき、$\mathcal{E}_{(x_i)_{i\in I}}\subseteq \mathcal{F}$は$\{\{x_i\mid i\gtrsim_I i_0\}\mid i_0\in I\}\subseteq \mathcal{F} $と同値になることを思い出してね。
$A\subseteq X,A \neq \varnothing $とする。
$A\in\mathcal{E}_{(x_i)_{i\in I}} \Longleftrightarrow (\exists (a_j)_{j\in J}:A$上ネット$)[(x_i)_{i\in I}\sim_{\text{Tail}}(a_j)_{j\in J}]$
$( \Longleftarrow )$：Tail同値の定義を確認しよう。
$( \Longrightarrow )$：問1で確認した$\left\uparrow(\cdot)\right.$の閉包作用素としての性質より
\begin{equation}
A\in\mathcal{E}_{(x_i)_{i\in I}} \Longleftrightarrow \{A\}\subseteq\mathcal{E}_{(x_i)_{i\in I}} \Longleftrightarrow \left\uparrow\{A\}\right.\subseteq\mathcal{E}_{(x_i)_{i\in I}}
\end{equation}
なので、まず$\left\uparrow\{A\}\right.$という真フィルターに対して定理1の証明と同じことをする。$\mathcal{B}=\{A\}$と置いてみよう。対応するネットは何になるかな？次に、定理2を見てみよう。
そろそろ慣れてきたかな？それじゃあ１問！
$x\in X$とする。真フィルター$\left\uparrow\{\{x\}\}\right.$に対応するネットはどんな形のネットかな？
対応するネットは、eventuallyフィルターが$\mathcal{E}_{(x_i)_{i\in I}}=\left\uparrow\{\{x\}\}\right.$になる任意のネットだ。では、具体的にはどんな形だろう？eventuallyフィルターとは、十分先を全部含む集合の一覧のことだった。今\begin{eqnarray*}
\left\uparrow\{\{x\}\}\right.\subseteq\mathcal{E}_{(x_i)_{i\in I}}&\Longleftrightarrow&\{x\}\in\mathcal{E}_{(x_i)_{i\in I}}\\
&\Longleftrightarrow&(\exists i_0\in I)[\{x_i\mid i\gtrsim_I i_0\}\subseteq\{x\}]
\end{eqnarray*}なので、十分先で全部$x$の一点をとるネットが対応するネットだ！（例えば、点列$(a,b,a,x,x,x,x,\cdots)$とか）
このとき、
\begin{eqnarray*}
\left\uparrow\{\{x\}\}\right.\supseteq\mathcal{E}_{(x_i)_{i\in I}}&\Longleftrightarrow&(\forall i_1\in I)(\exists i\gtrsim_I i_1)[x_i=x]
\end{eqnarray*}
は自動で満たす。$i_1\in I$を任意に固定したとき、これは上で述べた$i_0$と上に有向なので、$i_0,i_1\lesssim_I i_2$かつ$x_{i_2}=x$となる$i_2$が存在するからだ。なので、
\begin{eqnarray*}
\left\uparrow\{\{x\}\}\right.=\mathcal{E}_{(x_i)_{i\in I}}&\Longleftrightarrow&\left\uparrow\{\{x\}\}\right.\subseteq\mathcal{E}_{(x_i)_{i\in I}}
\end{eqnarray*}
となる（したがって極大真フィルター）。よって、求めるネットは十分先で全部$x$になるやつ及びそいつらに限る。
位相空間の定義
以下、諸概念の定義を簡単に紹介する。この章では、ネットの収束関係は全て公理〇を満たすものとする。つまり、真フィルターの収束関係に言い換えられるものだけを考える。以下の概念は真フィルターの言葉で定義されているが、真フィルターには(Tail同値な)ネットが対応しているので、すべてネット語に翻訳できることを念頭においてほしい。
集合$X$と真フィルターの収束関係$\searrow\:\subseteq\Phi(X)\times X$の組$(X,\searrow)$が
を満たすとき$(X,\searrow)$は前収束空間($\textsf{PreConv}$)であるといい、さらに
も満たすとき$(X,\searrow)$は収束空間($\textsf{Conv}$)であるという*5。
これらの公理をネット語に翻訳すると、$⓪$は「収束ネットの部分ネットは同じ点に収束する」、$➀$は「定値ネット(にTail同値なネット)は自身の点に収束する」という意味。
\begin{eqnarray*}\:\:\: \mathcal{N}(x)&\coloneqq&\{S\subseteq X\mid(\forall \mathcal{F}\in \Phi(X))[\mathcal{F}\searrow x \Longrightarrow S\in\mathcal{F}]\}\\ A^{\circ} &\coloneqq&\{x\in X\mid(\forall\mathcal{F}\in \Phi(X))[\mathcal{F}\searrow x \Longrightarrow A\in \mathcal{F}]\}\\ \overline{A} &\coloneqq&\{x\in X\mid(\exists\mathcal{F}\in \Phi(X))[\mathcal{F}\searrow x,A\in \mathcal{F}]\}\\ \mathcal{O}&\coloneqq&\{U\subseteq X\mid U=U^{\circ}\}\\ \mathcal{V}(x)&\coloneqq&\left\uparrow\{U\in\mathcal{O}\mid x\in U\}\right.\\ \text{Lim}(\mathcal{F})&\coloneqq& \{x\in X\mid\mathcal{F}\searrow x\} \end{eqnarray*}
ネット語に翻訳すると、内部は「その点に収束するネットが$A$上ネットしかない、そんな点の集まり」、閉包は「$A$上ネットの収束点全体」という意味。点$x\in X$の近傍フィルター$\mathcal{N}(x)$は「$x$に収束する全てのネットの十分先を含む集合の一覧」という意味。
$(X,\searrow)$を収束空間とする（つまり$⓪,➀$を満たす）
- Kent空間$\;\;: \Longleftrightarrow +②:\mathcal{F}\searrow x \Longrightarrow \mathcal{F} \cap \left\uparrow\{\{x\}\}\right.\searrow x$
- 極限空間$\;\;\; : \Longleftrightarrow +③:\mathcal{F},\mathcal{G}\searrow x \Longrightarrow \mathcal{F} \cap \mathcal{G}\searrow x$
- 擬位相空間$: \Longleftrightarrow +④:\mathcal{F}\searrow x \Longleftrightarrow (\forall \mathcal{U}\in\text{Ult}(X))[\mathcal{F}\subseteq\mathcal{U} \Longrightarrow \mathcal{U}\searrow x]$
- 前位相空間$: \Longleftrightarrow +⑤:\mathcal{F}\searrow x \Longleftrightarrow \mathcal{N}(x)\subseteq \mathcal{F}$
- 位相空間$\;\;\;: \Longleftrightarrow +⑥:⑤$かつ$\mathcal{N}(x)$が内部$( \cdot )^{\circ}$について閉じている
- $⓪,➀$を仮定したとき、⑤は「$\mathcal{N}(x)\searrow x$」や、「$\Lambda\neq \varnothing \text{ and }(\forall \lambda\in\Lambda)[\mathcal{F}_\lambda\searrow x ]\Longrightarrow \bigcap_{\lambda\in \Lambda}\mathcal{F}_\lambda \searrow x $」と同値になる。好みの定義を選んでいい。
- $⓪,➀$を仮定したとき、⑥は「$\mathcal{V}(x)\searrow x$」や、「⑤かつ$\mathcal{V}=\mathcal{N}$」、「⑤かつ$(\cdot)^{\circ}$が冪等」、「⑤かつ$\overline{(\cdot)}$が冪等」と同値になる。好みの定義を選んでいい。
それぞれ$\textsf{Kent},\textsf{Lim},\textsf{PsTop},\textsf{PreTop},\textsf{Top}$と表記する$[2]$。下に行くほど強い制約になる。
$\textsf{Kent}\supseteq\textsf{Lim}\supseteq\textsf{PsTop}\supseteq\textsf{PreTop}\supseteq\textsf{Top}$
つまり、位相空間とは集合にネットの収束関係を入れた構造のうち、$〇,⓪,➀,⑥$の４つの公理を満たすものである。もちろん、よく見られる開集合系や近傍系、閉包作用素、境界、開核....を使った定義と同値になる.（証明は容易）。時々、「この極限ってどんな位相を入れてるんですか？」と質問する人を見かけて混乱したことがあるかもしれないが、ここまで読めばこの「位相を入れる」とは「収束関係を入れる」という意味だったことが分かるね。位相は万能ではあるが、位相で表現できない収束も意外とある。例えば、可測関数列のほとんど至る所での収束は$\textsf{Top}$にも$\textsf{PreTop}$にもならず、$\textsf{PsTop}$になる。また、圏としての性質もよくはない。$\textbf{PsTop}$まではカルテシアン閉になるが、$\textbf{PreTop}$や$\textbf{Top}$はならない。
以下の重要な位相的性質も、収束関係で定義すると意味がとてもわかりやすくなる。
- $(X,\rightarrow)$はHausdolff$: \Longleftrightarrow $どんなネットも極限値は１個以下
- $(X,\rightarrow)$はコンパクト$: \Longleftrightarrow $どんなネットも収束部分ネットを持つ
- $(X,\rightarrow)$は局所コンパクト$: \Longleftrightarrow $どんな収束ネットも十分先でコンパクト集合に含まれる。つまり
$\text{Lim}((x_i)_{i\in I})\neq\varnothing\Longrightarrow(\exists A\colon\text{compact})(\exists i_0\in I)[\{x_i\mid i\gtrsim_I i_0\}\subseteq A]$ - $(X,\rightarrow)$は$T_0$$: \Longleftrightarrow $相異なる２点は収束関係で区別できる*3
↑これ以外にも位相空間論のありとあらゆる概念は収束関係を使って定義できる。なので、開集合など不要な概念だ。最後にいくつか例を挙げよう。
- 離散位相（自由$\textbf{Conv}$~$\textbf{Top}$）
$X$上に収束関係を
\begin{equation} \mathcal{F}\searrow x: \Longleftrightarrow \mathcal{F}=\left\uparrow\{\{x\}\}\right. \end{equation}
と定義すると$(X,\searrow)$は位相空間になる。これは$\textbf{Conv}$から$\textbf{Set}$への忘却関手の左随伴、いわゆる自由対象になる。 - 密着位相（余自由$\textbf{PreConv}$~$\textbf{Top}$）
収束関係を$\searrow \:\coloneqq\Phi(X)\times X$、つまり
\begin{equation} \mathcal{F}\searrow x: \Longleftrightarrow \top \end{equation}
と定義すると$(X,\searrow)$は位相空間になる。全ての点が収束関係で見て区別できない、同じ点に見える*4から、「密着」というのだろう。また、これは$\textbf{PreConv}$から$\textbf{Set}$への忘却関手の右随伴、いわゆる余自由対象になる。 - 空収束（自由$\textbf{PreConv}$）
収束関係を$\searrow \:\coloneqq \varnothing$、つまり
\begin{equation} \mathcal{F}\searrow x: \Longleftrightarrow \bot \end{equation}
と定義すると$(X,\searrow)$は前収束空間($\textsf{PreConv}$)になる。これは$\textbf{PreConv}$から$\textbf{Set}$への忘却関手の左随伴、いわゆる自由対象になる。 - 距離位相
$(X,d)$を距離空間、$B_d(x, \varepsilon )$を$x$の$\varepsilon$近傍とする。収束関係を
\begin{equation} \mathcal{F}\searrow x: \Longleftrightarrow \{B_d(x, \varepsilon )\mid\varepsilon>0\}\subseteq\mathcal{F} \end{equation}
と定義すると$(X,\searrow)$は位相空間になる。このとき$\mathcal{N}(x)=\mathcal{V}(x)=\left\uparrow\{B_d(x, \varepsilon )\mid\varepsilon>0\}\right.$になる。(距離位相を「$\varepsilon-n$論法的収束関係」と呼ぶ人もいる。$\mathcal{F}$がある点列に対応しているとき、この収束の定義は$\varepsilon-n$論法になるからだ。やめておいたほうがいいと思う) - 順序位相
$(X,\lt)$を(狭義)全順序集合、$(a,b)\coloneqq\{t\in X\mid a\lt t\lt b\}$を区間とする。収束関係を
\begin{equation} \mathcal{F}\searrow x: \Longleftrightarrow \{(a,b)\mid a,b\in X,x\in (a,b)\}\subseteq\mathcal{F} \end{equation}
と定義すると$(X,\searrow)$は位相空間になる。このとき$\mathcal{N}(x)=\mathcal{V}(x)=\left\uparrow\{(a,b)\mid a,b\in X,x\in (a,b)\}\right.$になる。 - 積位相（圏論的積）
普遍的構成の例も挙げよう。$\{(X_\lambda,\searrow_{X_\lambda})\}_{\lambda\in \Lambda}$を位相空間の族とする。直積集合$\displaystyle\prod_{\lambda\in \Lambda}X_\lambda$上に、収束関係を
\begin{equation} \mathcal{F}\searrow \boldsymbol{x} :\Longleftrightarrow (\forall \lambda\in \Lambda)[{\pi_\lambda}_*\mathcal{F}\searrow_{X_\lambda}\pi_\lambda(\boldsymbol{x})] \end{equation}
と定義すると、位相空間になる。つまり、成分ごとの収束で定める。ただし、$\pi_\lambda$は$\lambda$成分の射影、${\pi_\lambda}_*\mathcal{F}$は像フィルター(後述)とする。これは、$\{\pi_\lambda\}_{\lambda\in \Lambda}$を全て連続にする最大の(＝最粗の)位相空間になる。また、これは$\textbf{Top}$の圏論的積になる。ちなみに、$\textbf{Conv}$の圏論的積も全く同じ。
$\mathbb{R}$にユークリッド距離位相を入れる。$a< b$とする。
有界関数$f:[a,b]\rightarrow \mathbb{R}$がリーマン積分可能であるとは
\begin{eqnarray}
\left\{
\begin{array}{l}
I\coloneqq \big\{(\{x_0,x_1,\cdots,x_n\},(t_1,\cdots,t_n))\bigm| n\in \mathbb{N},a=x_0< x_1<\cdots x_n=b,t_k\in [x_{k-1},x_k]\big\}, \\
(P,\boldsymbol{t})\lesssim_I (P',\boldsymbol{t}'): \Longleftrightarrow P\subseteq P'
\end{array}
\right.
\end{eqnarray}
をラベル$(I,\lesssim_I)$とした$f$のリーマン和ネット$\mathcal{S}:I\rightarrow\mathbb{R};$
\begin{equation}
\mathcal{S}(P,\boldsymbol{t})\coloneqq \sum_{k=1}^n f(t_k) \cdot (x_k-x_{k-1})
\end{equation}
が収束すること。距離位相はHausdolffなので、ネットの極限は収束すれば一意。この一意に決まる極限値を$f$のリーマン積分と言い、$\displaystyle\int_{a}^{b} f(x)dx$と表記する。
（リーマン和ネットをeventuallyフィルターで送って例1-4の収束の定義に当てはめればいい）
（$\mathbb{R}^d$の場合は、単に閉区間の分割$P$を閉短形の分割に拡張すればいい。）
最後に問題形式で
- $\mathcal{F}\in\Phi(X)$、$f:X\rightarrow Y$を写像とすると、
\begin{eqnarray*} f_*\mathcal{F} &\coloneqq& \left\uparrow\{f[A]\mid A\in \mathcal{F}\}\right. \\ &=&\{B\subseteq Y\mid f^{-1}[B]\in\mathcal{F}\} \end{eqnarray*}
は$Y$の真フィルターになることを示してみよう。これを$f$の像フィルターと呼ぶ。明らかに、単調性$\mathcal{F}\subseteq\mathcal{G}\Longrightarrow f_*\mathcal{F}\subseteq f_*\mathcal{G}$を満たす。 - $X$上のネット$(x_i)_{i\in I}$に対応する真フィルターは$\mathcal{E}_{(x_i)_{i\in I}}$だった。$(x_i)_{i\in I}$の各成分を関数$f:X\rightarrow Y$で移した$Y$上のネット$(f(x_i))_{i\in I}$に対応する真フィルターは、$\mathcal{E}_{(f(x_i))_{i\in I}}=f_*\mathcal{E}_{(x_i)_{i\in I}}$と書けることを確かめてみよう。ここから、２つのTail同値なネットにそれぞれ関数を噛ませて移してもTail同値になることが分かる。
\begin{xy} \begin{array}{c@{\hspace{4em}}c} \xymatrix { \text{Net}(X) \ar[d]_{(\text{id},f\circ(\cdot))} \ar@{->>}[r]^{\mathcal{E}_\bullet}& \Phi(X) \ar[d]^{f_*(\cdot)} \\ \text{Net}(Y) \ar@{->>}[r]_{\mathcal{E}_\bullet} & \Phi(Y) \ar@{}[lu]|{\circlearrowright} } & \xymatrix{ (x_i)_{i\in I} \ar@{|->}[d]_{f\circ(\cdot)} \ar@{|->}[r]^{\mathcal{E}_\bullet}& \mathcal{E}_{(x_i)_{i\in I}} \ar@{|->}[d]^{f_*(\cdot)} \\ (f(x_i))_{i\in I} \ar@{}[r]^(.34){}="a"^(.75){}="b" \ar@{|->} "a";"b"_{\mathcal{E}_\bullet} & *+[r]{\hskip-0.94em\mathcal{E}_{(f(x_i))_{i\in I}}=f_*\mathcal{E}_{(x_i)_{i\in I}} } \ar@{}[lu]|{\circlearrowright} } \end{array} \end{xy} - 連続写像の定義を、真フィルターの収束関係を使って言い換えてみよう。
- $(X,\searrow_X),(Y,\searrow_Y)$が$\textsf{PreTop}$のとき、写像$f:X\rightarrow Y$が連続であることと$(\forall x\in X)[\mathcal{N}_Y(f(x))\subseteq f_*\mathcal{N}_X(x)]$は同値になることを示してみよう。
- $X,Y$に距離位相が入っているとき、$f$の連続性は$\varepsilon-\delta$論法による連続の定義に一致することを確かめてみよう。
いいねください
追記 〈便利な記法〉
- $\mathcal{F}\in\Phi(X)$と$f:X\rightarrow Y$に対して
\begin{eqnarray} \lim_\mathcal{F}f&\coloneqq&\text{Lim}(f_*\mathcal{F})\\ &=&\{y\in Y\mid f_*\mathcal{F}\searrow_Y y\} \end{eqnarray} - $x_0\in X$と$f:X\rightarrow Y$に対して
\begin{eqnarray*} \lim_{x\rightarrow x_0}f(x)&\coloneqq& \begin{dcases} \bigcap_{\substack{\mathcal{F}\in\Phi(X)\\\mathcal{F}\searrow_X x_0}}\lim_{\mathcal{F}}f&(\text{$x_0$ に収束する $\mathcal{F}\in \Phi(X)$ が存在する})\\[5pt] \:\:\,Y&(\text{存在しない}) \end{dcases}\\[9pt] &=&\{y\in Y\mid (\forall \mathcal{F}\in\Phi(X))[\mathcal{F}\searrow_X x_0\Longrightarrow f_*\mathcal{F}\searrow_Y y]\}\\ \end{eqnarray*} - $A\subseteq X,x_0\in X$と$f:X\rightarrow Y$に対して
\begin{equation} \lim_{\substack{x\rightarrow x_0\\x\in A}}f(x)\coloneqq \{y\in Y\mid (\forall \mathcal{F}\in\Phi(X))[A\in\mathcal{F}\searrow_X x_0\Longrightarrow f_*\mathcal{F}\searrow_Y y]\} \end{equation}
（↑$x_0\notin\overline{A}$のとき$Y$）
$X,Y$に収束関係が入っているとする。関数$f:X\rightarrow Y$が$x_0\in X$で連続であるとは、
\begin{equation}
f(x_0)\in\lim_{x\rightarrow x_0}f(x)
\end{equation}
なことと定義する。
$X,Y$に収束関係が入っているとする。関数$f:X\rightarrow Y$が連続写像であることと、任意の点$x_0\in X$で連続であることは同値
\begin{equation} \coprod_{\lambda\in\Lambda}A_\lambda=\bigcup_{\lambda\in\Lambda}\{\lambda\}\times A_\lambda \end{equation}
↩
・冪集合の同一視：$\mathcal{P}(Z)\overset{\chi_\bullet}{\underset{(\cdot)^{-1}[\{1\}]}{\cong}}\text{Map}(Z,\{0,1\})$
・商の普遍性：$\text{Map}(X/{\sim},\cdot)\overset{(\theta_y)_{y\in\textbf{SET}}}{\cong}\{f\in\text{Map}(X,\cdot)\mid(\forall a,b\in X)[a\sim b\Longrightarrow f(a)=f(b)]\}\;\;\;\big((\theta_y)_{y\in\textbf{SET}}=((\cdot)\circ\pi)_{y\in\textbf{SET}}\text{は射影}\pi\text{を合成した自然変換。※米田の補題は使っていない。}\big)$
・カリー化：$\text{Map}(X\times Y,Z)\cong\text{Map}(X,\text{Map}(Y,Z))$
\begin{eqnarray*} \mathcal{P}(\Phi(X)\times X)&\cong&\mathcal{P}(\text{Net}(X)/{\sim_\text{Tail}}\times X)\\ &\cong&\text{Map}(\text{Net}(X)/{\sim_\text{Tail}}\times X,\{0,1\})\\ &\cong&\text{Map}(\text{Net}(X)/{\sim_\text{Tail}},\text{Map}(X,\{0,1\}))\\ &\cong&\{g\in\text{Map}(\text{Net}(X),\text{Map}(X,\{0,1\}))\mid(\forall (x_i)_{i\in I},(y_j)_{j\in J}\in \text{Net}(X))[(x_i)_{i\in I}\sim_\text{Tail} (y_j)_{j\in J}\Longrightarrow g((x_i)_{i\in I})=g((y_j)_{j\in J})]\}\\ &\cong&\{f\in\text{Map}(\text{Net}(X)\times X,\{0,1\})\mid(\forall (x_i)_{i\in I},(y_j)_{j\in J}\in \text{Net}(X))[(x_i)_{i\in I}\sim_\text{Tail} (y_j)_{j\in J}\Longrightarrow f((x_i)_{i\in I},\cdot)=f((y_j)_{j\in J},\cdot)]\}\\ &=&\big\{f\in\text{Map}(\text{Net}(X)\times X,\{0,1\})\mid(\forall (x_i)_{i\in I},(y_j)_{j\in J}\in \text{Net}(X))\big[(x_i)_{i\in I}\sim_\text{Tail} (y_j)_{j\in J}\Longrightarrow (\forall \alpha\in X)[f((x_i)_{i\in I},\alpha)=f((y_j)_{j\in J},\alpha)]\big]\big\}\\ &=&\big\{f\in\text{Map}(\text{Net}(X)\times X,\{0,1\})\mid(\forall (x_i)_{i\in I},(y_j)_{j\in J}\in \text{Net}(X))\big[(x_i)_{i\in I}\sim_\text{Tail} (y_j)_{j\in J}\Longrightarrow (\forall \alpha\in X)[f((x_i)_{i\in I},\alpha)=1\Longleftrightarrow f((y_j)_{j\in J},\alpha)=1]\big]\big\} \;(\text{∵}f\text{は}0\text{か}1\text{しか値を取らぬ故})\\ &\overset{(\cdot)^{-1}[\{1\}]}{\cong}&\big\{\rightarrow\in\mathcal{P}(\text{Net}(X)\times X)\mid(\forall (x_i)_{i\in I},(y_j)_{j\in J}\in \text{Net}(X))\big[(x_i)_{i\in I}\sim_\text{Tail} (y_j)_{j\in J}\Longrightarrow (\forall \alpha\in X)[(x_i)_{i\in I}\rightarrow\alpha\Longleftrightarrow (y_j)_{j\in J}\rightarrow\alpha]\big]\big\} \end{eqnarray*}↩
