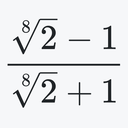3
単位円の内外で別の有理関数に収束する級数
139
0
$$\newcommand{acoloneqq}[0]{\ &\hspace-2pt\coloneqq}
\newcommand{ar}[1]{\operatorname{ar{#1}}}
\newcommand{arc}[1]{\operatorname{arc{#1}}}
\newcommand{asupplement}[1]{&\hspace{#1}\textsf}
\newcommand{beginend}[2]{{\begin{#1}#2\end{#1}}}
\newcommand{bm}[0]{\boldsymbol}
\newcommand{bscolor}[1]{\color{var(--bs-#1)}}
\newcommand{bscolorbox}[1]{\colorbox{var(--bs-#1)}}
\newcommand{bsrowcolor}[1]{\rowcolor{var(--bs-#1)}}
\newcommand{bt}[1]{{\because\textsf{#1}}}
\newcommand{C}[0]{\mathbb C}
\newcommand{Defarrow}[0]{\xLeftrightarrow{\textrm{def}}}
\newcommand{fqty}[0]{\!\qty}
\newcommand{hcfrac}[3]{{\frac{#1}{#2}\!\genfrac{}{}0{}{}{#3}\!}}
\newcommand{hen}[1]{{(\textrm{{#1}辺})}}
\newcommand{hygeo}[6]{{{}_{#1}{#2}_{#3}{\qty[\beginend{matrix*}{#4\\ #5}\ ;{#6}]}}}
\newcommand{ifc}[0]{\operatorname{if}}
\newcommand{In}[0]{\in\mathbb}
\newcommand{kfrac}[0]{\mathop{\Large\raise-.8pt{\textrm K}}}
\newcommand{Kfrac}[0]{\mathop{\huge\raise-2.2pt{\textrm K}}}
\newcommand{kome}[0]{\textreferencemark}
\newcommand{leftshiftarrow}[0]{{\substack{\curvearrowright\\ \leftharpoondown}}}
\newcommand{lr}[3]{{\left#1{#2}\right#3}}
\newcommand{lvvr}[2]{\lr{#1}{\negmedspace\lr|{#2}|\negmedspace}}
\newcommand{N}[0]{\mathbb N}
\newcommand{newop}[1]{\DeclareMathOperator{#1}{#1}}
\newcommand{ot}[0]{\leftarrow}
\newcommand{otherwise}[0]{\textrm{otherwise}}
\newcommand{P}[0]{\mathbb P}
\newcommand{Q}[0]{\mathbb Q}
\newcommand{qb}[0]{{\quad\because}}
\newcommand{qbt}[1]{{\quad\because\textsf{#1}}}
\newcommand{R}[0]{\mathbb R}
\newcommand{RANGE}[0]{}\newcommand{rangeex}[6][,]{{#2{#3}_{#5}#4#1\cdots#1#2{#3}_{#6}#4}}\newcommand{range}[2][,]{\rangeex[#1]{}{#2}{}}{}
\newcommand{REQUIRE}[0]{}\require{physics}{}
\newcommand{rightshiftarrow}[0]{{\substack{\curvearrowleft\\ \rightharpoondown}}}
\newcommand{rprod}[0]{\mathop{\prod\!\llap\coprod}}
\newcommand{sahen}[0]{\hen左}
\newcommand{STIRLING}[0]{}\newcommand{stirling}[3][]{{\qty[\beginend{matrix}{{#2}\\ {#3}}{#1}]}}\newcommand{Stirling}[3][]{{\qty{\beginend{matrix}{{#2}\\ {#3}}{#1}}}}{}
\newcommand{uhen}[0]{\hen右}
\newcommand{vbin}[1]{\mathbin{{#1}\!\llap|\ }}
\newcommand{Z}[0]{\mathbb Z}
\newcommand{zzCOMPLEXPARTS}[0]{}\let\Re\relax\newop{Re}\let\Im\relax\newop{Im}{}
$$
興味深い例を 特殊関数グラフィックスライブラリー で見つけたので証明します。
$\displaystyle \sum_{n=1}^\infty \frac{z^{n-1}}{(1-z^n)(1-z^{n+1})} = \beginend{cases}{ \dfrac1{(1-z)^2} &|z|<1 \\ \dfrac1{z(1-z)^2} &|z|>1 }$
$\beginend{align}{ \sahen &= \frac1{1-z}\sum_{n=1}^\infty \qty(\frac{z^{n-1}}{1-z^n}-\frac{z^n}{1-z^{n+1}}) \\&= \frac1{1-z}\lim_{N\to\infty} \fqty(\frac1{1-z}-\frac{z^N}{1-z^{N+1}}) \\&= \uhen }$
参考文献
投稿日:2024年1月27日
更新日:2024年2月7日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中