量子コンピュータにおける素因数分解(1): 加算器

【修正履歴】

• 7Aug.2024 以下 koumei さんにご指摘頂きました:
  ・CNOTゲートとCCNOTゲートによる変換の説明の追記
  ・Sumゲートの真理値表の修正
  ・図5 carryゲートの図の修正（2つめのCCNOTゲートの黒丸の位置が間違っていました）
  ${}$

量子コンピュータによる素因数分解

近年量子コンピュータ（Quantum Computer, 以下QCと略す）の進化が目覚ましいです。

QCの性能向上の主要課題として、量子ビットを増やすこととエラーを減らすことが挙げられます。前者に関しては現在1000量子ビットを超えるQCが作成されています gigazine。後者に関しては昨年Googleが「量子誤り符号訂正」という技術を実際のQCで実現したことが大きなニュースとなりました nikkei。どちらも着実な進歩を遂げています。大衆への普及の観点では、IBMのQCは一般人でも無料で使用できます IBM。私もこれを使ってMathlogに記事を書きました Mathlog。このようなQCの発展は、10〜20年前には考えられなかったと思います。

ただしQCが古典コンピュータに対して実用的な課題おいて優位性を示すような状況にはまだまだ遠いです。私も詳しくはないですが、例えば最も早く実用化ができそうな応用分野である化学の計算でも、QCの優位性を示すには数万から数十万の量子ビットが必要だそうです。また実用化すれば非常にインパクトが大きいと思われる暗号解読に関しては更に多くの量子ビット（数百万程度？）が必要とのことです。

これからいくつかの記事で、量子コンピュータの応用として最も有名であろう素因数分解のアルゴリズムである「Shorのアルゴリズム」に関し、自身の勉強ノートがてら書こうと思います。よく知られているように、現在最も安全な暗号化技術のひとつであるRSA暗号では、大きな桁の因数分解が古典コンピュータでは殆ど"不可能"であることを用いています。もう少し定量的なことをいうと、2進数で$L$桁の数の因数分解は古典コンピュータでは$L$の多項式時間ではできないと考えられています。一方Shorのアルゴリズムでは多項式時間（$\mathcal{O}(L^3)$くらい）で計算することが可能です（Hosoya P69）。

一連の記事の構成は以下のような感じです（01Sep.2024現在）：

1. 加算器（本記事）
2. べき剰余
3. 量子フーリエ変換
4. アルゴリズムの方針 & 関連定理
5. 位数推定と量子干渉

このうち4.5.を読めばShorのアルゴリズムは基本的には理解できます。1.から3.はアルゴリズムに必要な回路の構成に関する説明です。

主に参考とする文献は以下です：

• Shor, P. W., "Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer," SIAM Review, vol.41, 2 (1999); arXiv:quant-ph/9508027. Shor
• Vedral, V., V., Barenco, A. and Ekert, A., "Quantum networks for elementary arithmetic operations," Phys. Rev. A 54, 147–153 (1996). Vedral
• M.A.Nielsen & I.L.Chuang, "Quantum Computation and quantum Information (10th Anniversary Edition)," Cambridge University Press (2010). Nielsen
• 細谷暁夫、「量子コンピュータの基礎（第２版）」SGCライブラリー69、サイエンス社 Hosoya
• 量子アルゴリズムの基本：Shorのアルゴリズムの確認（その１） 、SamN、Qiita Qiita

最後のQiita記事ではとてもわかりやすく丁寧にShorのアルゴリズムが解説されています。また量子回路を古典コンピュータでシミュレーションして動作の確認もされています。

量子コンピュータと量子アルゴリズム

最初にQCの基礎的なことを述べておきます。

QCとは、計算を達成するように初期の量子状態にユニタリー変換を作用させ、出力状態から求める情報を読み出す装置です。この装置はいくつかの基礎的なユニタリー変換 −量子ゲートと呼ばれる− により構成されます。QCも（ふつうは）古典コンピュータと同様2進数を用いて計算を行います。2進数のビットにはスピンアップ・ダウンのような2値をとる状態を対応させます。これはqubitと呼ばれます。複数桁を表現するには量子状態の直積を用います。

量子コンピュータはどんな問題でも速く計算できるわけではないです。問題ごとにうまい量子アルゴリズムを見出し、それをQCに実装する必要があります。本記事で扱う素因数分解に関してはそのようなアルゴリズムが存在します。それが「Shorのアルゴリズム」です。量子コンピュータ実機での計算も行われているのですが、まだ2桁の整数の素因数分解にとどまっているようです。

少し余談になるのですが、量子アルゴリズムにおいて、重要だけど一般にはあまり意識されていないことがあります。これを標語的に言えば「結果を実際に観測して知るまでが量子アルゴリズム」ということになるかと思います。どういうことかというと、欲しい量子状態、すなわち計算結果の情報を持つ状態を作るだけではダメで、それを観測して実際に知ることまで含めて速く行えないと意味がない、ということです。良い例が「量子フーリエ変換（Quantum Fourier Transform, QFT）」です。QFTは古典的なフーリエ変換より本質的に速いと言われます。しかしそれは、ある状態に対してそれをフーリエ変換した量子状態を作ることが速いということであり、そこから実際にフーリエ変換の情報を読み出すのは大変な時間がかかってしまいます（ この記事 参照のこと）。QFTはそれ単独で使うものではなく、他のアルゴリズムの部品として用いるものです。実際これから述べるように、ShorのアルゴリズムではQFTを利用します。そしてShorのアルゴリズムでは素因数を実際に観測する過程まで含めて古典的なアルゴリズムより速いことが示されていますHosoya。

基礎的な回路

本章では基礎的な量子ゲートを導入します。

そのために量子コンピュータにおける数の取り扱いを具体的に述べておきます。$|0\rangle,|1\rangle$という2値の状態を用意します。この2値状態の多数の直積を用意し、それぞれにラベル$i$をつけてブラケット記法で$|0\rangle_i \ (i=0,1,2,\cdots N)$のように表すことにします。ある数$a$の2進数表示の$i$桁目のビットを$a_i\in \{0,1\}$としたとき、すなわち$a\leftrightarrow a_{N-1}a_{N-2}\cdots a_{1}a_{0}$とすると
\begin{align} \hspace{1.5cm} a\text{を}\ \ |a\rangle \leftrightarrow |a_{N-1}\rangle_{N-1}\otimes |a_{N-2}\rangle_{N-2}\otimes\cdots\otimes|a_1\rangle_1\otimes |a_0\rangle_0 \ \ \text{に対応させる} \end{align}
ことにします。以下では直積の記号$\otimes$やブラケットのsuffixを取り除いて
\begin{align} \hspace{1.5cm} |a_{N-1}\rangle|a_{N-2}\rangle\cdots |a_1\rangle|a_0\rangle \end{align}
と書くことにします。各桁の量子状態をqubitと呼びます。ちなみにふつう一番下の桁は「1桁目」と呼びますが、そうすると桁の呼び方と$a_i$の$i$との対応が1つずれ本質的でないややこしさが生じるので、本記事では一番下の桁を「0桁目」と呼ぶことにします。

前記したように、量子コンピュータではこの量子状態にユニタリー変換を作用させて目的の量子状態を作ります。ユニタリー変換は基本的な変換の素子からなり、この基本素子を量子ゲートと呼びます。変換はユニタリーなので逆変換が存在します。量子回路は左から右に状態を変換させていきますが、逆に右から左に変換させることが可能です。

ここから基本的なゲートを見ていきます。

NOT

量子回路図ではゲートを図で表します。NOTゲートは以下のように表します：

NOTゲートの量子回路図

これはビットを反転させる変換です。入力が1 qubit（$a$）、出力が 1 qubit（$a'$）であり、以下の真理値表のように量子状態を変化させます：

\begin{array}{|c|c|} \hline a&a'\\ \hline 0 & 1\\ 1 & 0\\ \hline \end{array}

以降プライムは、プライムなしqubitに対応するoutputを表します。

Control-NOT（CNOT）

Control-NOT (CNOT) ゲートにはinput qubitが2つ、output qubitが2つあります。input qubitはcontrol qubitとtarget qubitに分類され、control qubitが1のときにtarget qubitを反転させます。

以下$c$をinputのcontrol qubit, $t$をinputのtarget qubitとします。CNOTゲートの回路図と真理値表は以下のようになります：

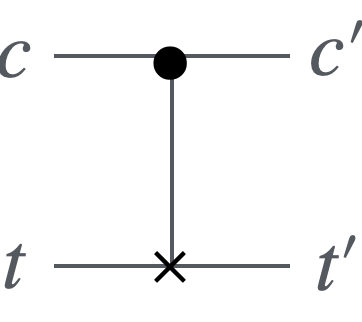CNOTゲートの量子回路図

\begin{array}{|c|c|} \hline c&t&c'&t'\\ \hline 1 & 0 & 1 & 1\\ 1 & 1 & 1 & 0\\ \hline \end{array}

この表にない入力状態の場合（$c=0,t=0$及び$c=0,t=1$）、出力は入力と全く同じです。
以下真理値表は入力と出力が違う非自明な組み合わせのみ記すことにします。
また以降他のゲートでも黒丸はcontrol、バツ印はtarget qubitを表すことにします。

結局CNOTゲートは
\begin{align} \hspace{1.5cm} |c\rangle|t\rangle\to |c\rangle|c\oplus t\rangle \end{align}
という変換を行うゲートです。

Control-contlol-NOT (CCNOT, Toffoli gate)

これはcontrolが2つあるNOTゲートであり、controlが2つとも1のときのみtargetを反転させます：

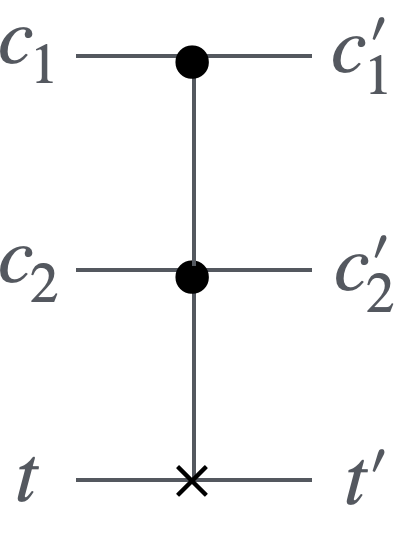CCNOTゲートの量子回路図

\begin{array}{|c|c|} \hline c_1&c_2&t&c'_1&c'_2 &t'\\ \hline 1 & 1 & 0 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 & 1 & 0\\ \hline \end{array}

これはToffoliゲートとも呼ばれます。

結局CCNOTゲートは
\begin{align} \hspace{1.5cm} |c_1\rangle|c_2\rangle|t\rangle\to|c_1\rangle|c_2\rangle|c_1 c_2\oplus t\rangle \end{align}
という変換を行うゲートです。

Sum

これはmod 2で足し算を行うゲートです。すなわち
\begin{align} \hspace{1.5cm} |a\rangle|b\rangle|c\rangle \xrightarrow{\text{sum}}|a\rangle|b\rangle|a\oplus b\oplus c\rangle \end{align}
という変換を行います。ここで$\oplus$は$\text{mod }2$での足し算を表します。

このゲートは以下のようにCNOTゲートを2つ組み合わせることで作れます：

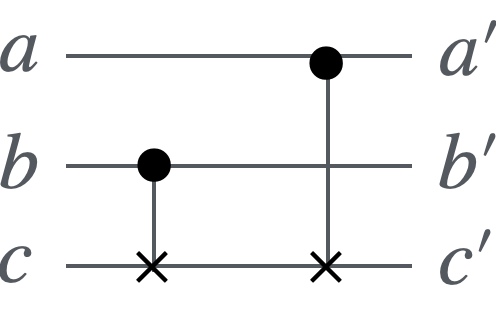Sumゲートの量子回路図

\begin{array}{|c|c|} \hline a & b & c & a' & b' & c'\\ \hline 1 & 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 0 & 0 & 1 & 1\\ 0 & 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 1 & 0 & 0\\ \hline \end{array}

Carry (桁上り)

sumゲートは1ビットの足し算をmod 2で行うゲートでした。ちゃんとした足し算を実現するには、桁上りを考慮する必要があります。そのためのゲートがcarryゲートです。

このゲートによる変換は次のように表せます：
\begin{align} \hspace{1.5cm} |c\rangle|a\rangle|b\rangle|d\rangle \xrightarrow{\text{carry}}|c\rangle|a\rangle|a\oplus b \rangle |(ca\oplus ab\oplus bc)\oplus d\rangle \tag{1} \end{align}

回路図と真理値表は以下のようになります：

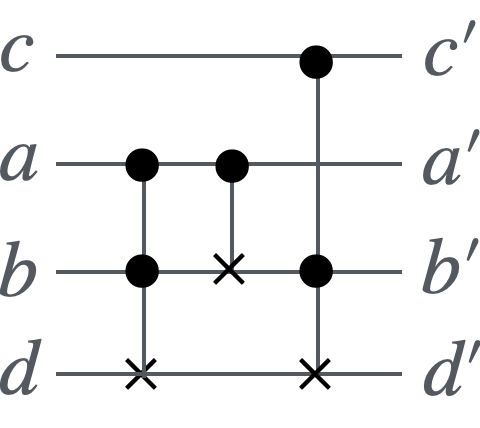Carryゲートの量子回路図

\begin{array}{|c|c|} \hline c&a&b&d&c' &a'&b'&d'\\ \hline 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1\\ 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1\\ 1 & 1 & 0 & 1 & 1 & 1 & 1 & 0\\ 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1\\ \hline \end{array}

carryゲートはCCNOTゲート2つとCNOTゲート1つから構成できます。

いま$d=0$にセットすると、Eq.(1)の一番右のqubitはcarryを行ったのち
\begin{align} \hspace{1.5cm} |ab\oplus bc\oplus ca\rangle \end{align}
になります。これは桁上りを表しています。 実際、2進数$a_{N-1}a_{N-2}\cdots a_1 a_0$と$b_{N-1}b_{N-2}\cdots b_1 b_0$に対し、$i$桁への桁上りを$c_{i}$とすると、$c_{i+1}$は$a_i,b_i,c_i$のうち0コまたは1コが1のとき0、2コまたは3コが1のとき1です。2進数の筆算を思い浮かべると、これが桁上りに相当することはわかると思います。そして上の表および式は実際これを実現しています。

Adder(加算器)

前章のゲートを組み合わせて、$a\leftrightarrow a_{n-1}a_{n-2}\cdots a_1a_0$と$b\leftrightarrow b_{n-1}b_{n-2}\cdots b_1b_0$の足し算を実現する量子回路を作ります。

Ref.Vedral, Figure 2ではこれを実現する量子回路として以下のようなものを提示しています：
加算器（Adder）の量子回路図。Ref.[6] Figure 2を参考に、回路図に量子状態の遷移を書きこんだもの。黒い長四角はcarryゲート、黄土色の長四角はsumゲートを表す。CNOTより左側のcarryゲート群をA群、CNOTを含めて右側のゲート群をB群と呼ぶことにする。

黒い縦長四角はcarryゲート、黄土色の四角はsumゲートを表します。水色の数字は各桁の桁上り用ビットを、マゼンタの数字は$a,b$各桁のそれぞれのビット$a_i,b_i$を表します。これらは実際は量子状態であることに注意してください（ブラケットを省略している）。線の上に書かれている数字・変数は、各ゲートによる状態変化を示しています。

真ん中に1つだけCNOTゲートが存在します。これより左のcarryゲート群をA群、CNOTゲートを含めた右側をB群と呼ぶことにします。

図6を見れば何をやっているかわかると思いますが、以下詳しく説明しておきます：

最終的に図6で赤い太字にしてあるqubitおよび一番下の$c_n$（最上位ビット）を見れば、$n$桁の2進数同士の和が完成していることがわかります。

前述したようにこの回路はユニタリー変換なので逆回しができます。右に$n$桁の2進数を2つセットして左に変換していけば、2つの数の引き算ができます。

量子効果の重要性

ここまでの話をみるとあまり量子的な要素がないように見えます。もちろん各qubitは量子状態なのでそういう意味では量子的ですし、各量子ゲートは実際には量子効果を用いてユニタリー変換を実現しています(Ref.Hosoya P33)。が、べつに量子状態を用いずに古典的な論理回路だと考えても本質的に違いがないように思います。

量子効果が重要なことのひとつに、重ね合わせの状態を用いることができることが挙げられます。何らかの計算を実行するとき、初期状態に計算したい数をぜんぶ重ね合わせておけば、1つの数のみの初期状態と同じ計算量でいっぺんに欲しい情報をもつ状態が得られます。ただし結果も重ね合わせになるので、結果状態から欲しい情報だけうまく抽出する必要があります。

加算器の回路図では量子状態がすべて各qubitの直積で書けるため、それぞれのqubitの線の上に量子状態を書いて状態遷移を表現することができました。しかしながら一般にはそうは書けません。例えば加算器でも初期状態を$|0\rangle,|1\rangle$の重ね合わせにした場合、qubit同士がエンタングルした状態になります。エンタングルしたqubit全体は「絡まって」おり、分離して書けません。このような状態は量子力学特有であり重要です。

${}$

今回はこれでおしまい & つづく。${}_\blacksquare$