何が「自然」なのか？

こんにちは。今回は以下の補題について考えます。

今回、論証の鍵になるのは「互いに素」や「多項式」などの条件をどのように扱うかです。

$ $

「多項式」をどう扱うか

多項式は「次数」の概念を持つ式であり、以下次数に注目した議論を展開したいところです。

$f(x),g(x)$の次数をそれぞれ$n,m$とすると、任意の$n,m$に対して題意を証明する問題となり、数学的帰納法が視野に入ります。実はここで数学的帰納法を選択するのには合理的な理由があります。

$ $

多項式と帰納法

数学的帰納法の証明は漸化式と構造が同じです。例えば、

$$ 　　　　　　　　a_{n+2}=f(a_{n},a_{n+1})$$

という漸化式があるのなら、帰納法のドミノ倒しの構造が、$n,n+1$番目を倒すことで、$n+2$番目も倒れるといった具合です。帰納法の本体の証明においては、漸化式を使って番号を下げて仮定を使うことになります。

$ $

今回は$n,m$で帰納法を回したいので、次数についての漸化構造ができれば良いわけですが、多項式が持つ次数は

• 微分する
• 階差をとる
• 割り算をする

など色々な方法で漸化構造を作ることが出来ます。

例えば、任意の$n\in\mathbb{N}$で$p(n)\Rightarrow q(n)$が成立することを証明するのに、$n=k$での成立を仮定して$n=k+1$での成立を証明するような状況を考えてみましょう。

階差を取る場合は、以下の図$1$のように、階差をとって次数を下げることによって数学的帰納法の仮定を使い、最後に階差の逆操作である$\sum$をとれば、$n=k+1$での証明が実現します。「微分」↔︎ 「積分」なども「階差」↔︎ 「Σ」と関係は同じなので同様に議論ができますね。

$ $

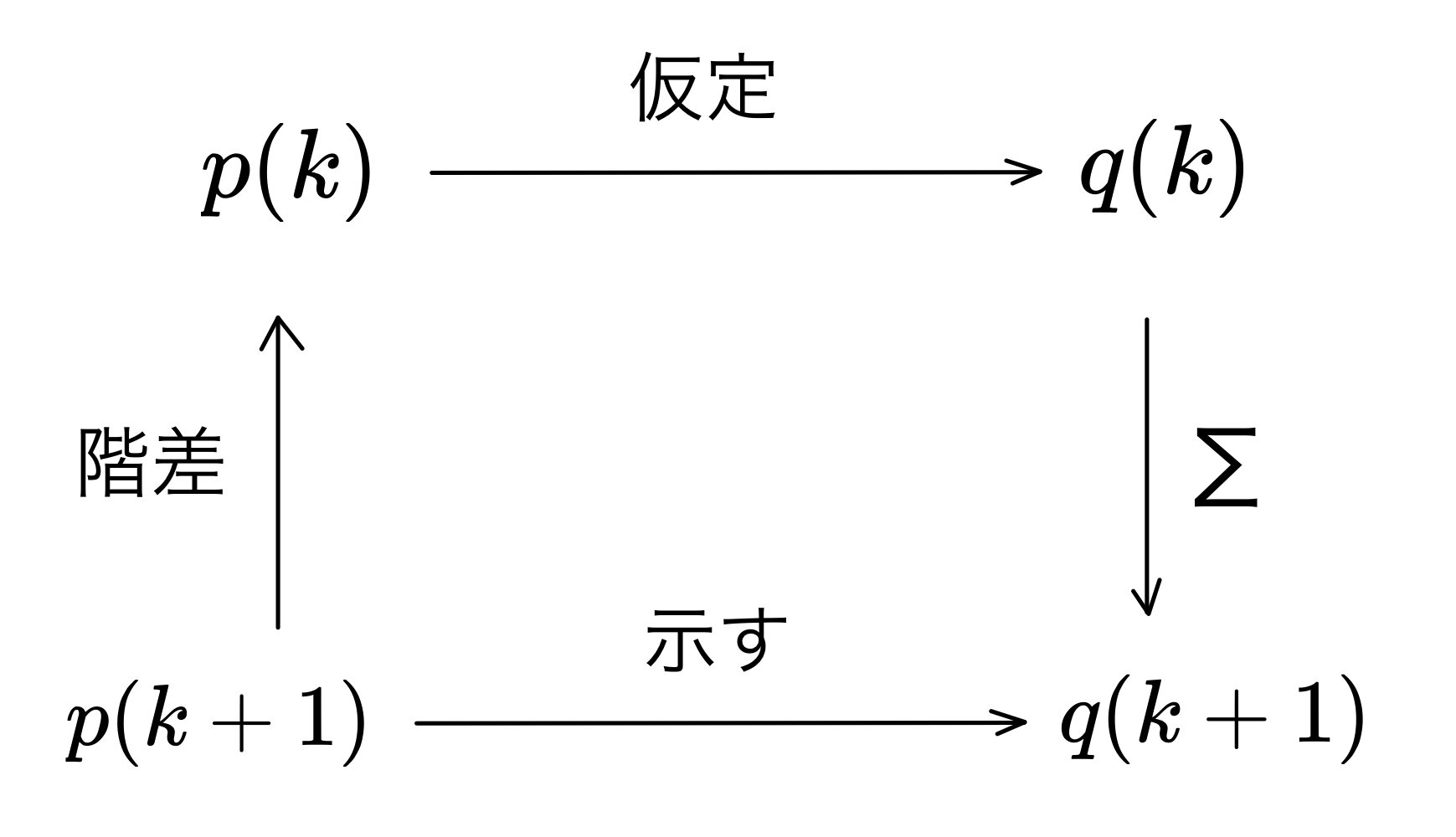数学的帰納法と次数の関係

$ $

$ $

まず、$f_1(x),g_1(x)$をそれぞれ、$n-1,m-1$次以下の多項式として、
$$ 　　　　　　f(x)=a_n x^n+f_1(x)~,~g(x)=b_m x^m+g_1(x) $$

とおきます。

$n$個の整数が互いに素を直接示すのは難しいので、ここでは背理法で示します。$f(x)g(x)$の全係数が共通素因数$p$を持つと仮定すると、$a_nb_m$は$p$の倍数です。$p$は素数なので、$a_n,b_m$のどちらかは$p$の倍数ですが、対称性より$a_n$が$p$の倍数としても問題ありません。ここで、
$$ 　　　　　　f(x)g(x)=a_nx^ng(x)+f_1(x)g(x) $$
であり、仮定より、$f(x)g(x),a_nx^ng(x)$の各係数は共通素因数$p$を持つので、$f_1(x)g(x)$の各係数は共通素因数$p$を持ちます。

帰納法の仮定として、$n+m$次未満での題意の成立を仮定すると、$f_1(x)g(x)$の次数が$n+m$未満であることに注意して、題意の対偶と、$p$が素数であることから、

　・$f_1(x)$の全係数が$p$の倍数
　・$g(x)$の全係数が$p$の倍数

のいずれかが成立します（$p$が素数なので、「原始多項式でない」だけではなく、$p$の倍数まで強められていることに注意）。

後者は、$f(x)$が原始多項式であることに矛盾し、前者も、$f(x)$が原始多項式であること及び$a_n$が$p$の倍数であることに矛盾します。

残り、ドミノ倒しの初期値は適当に倒しといてください。

$ $

＜ヒント＞
$2$階微分によって次数を下げると仮定が使えますね。

$ $

最後に

最後まで読んでいただきありがとうございました。
なお、この問題は、別証明として、Qualtaghさんの記事

https://mathlog.info/articles/4078

で紹介されているような解法も考えられます。要は「整数」条件に引っ張られてみるとこのような解法になり、「多項式」条件に引っ張られてみると本記事のような解法になるのかなと思います。

いずれにしても大切なことは、各概念の定義をしっかりと理解した上でそれを適切に咀嚼し、「何が自然なのか？」を考えることだと思います。

最後まで読んでいただきありがとうございました！

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $

$ $