東大数学2024第3問の代数的解釈
はじめに
こんにちは. 今回はタイトルの通り, 今年の東大数学の第3問が代数的に面白い解釈ができるというお話をしていこうと思います. 東大の過去問を見たくないという方にとってはネタバレ注意です!
この内容は, inspired by AKITOさんのツイート です. 感謝申し上げます.
${}$
群に関する基本事項を分かっていると楽ですが, そうではない高校生にもなんとなく分かるように説明をしていこうと思います.
それでは早速, 問題を見ていきましょう.
座標平面上を次の規則(i), (ii)に従って$1$秒ごとに動く点$\mathrm{P}$を考える.
(i)最初に, $\mathrm{P}$は点$(2,1)$にいる.
(ii)ある時刻で$\mathrm{P}$が点$(a,b)$にいるとき, その$1$秒後には$\mathrm{P}$は
- 確率$\dfrac13$で$x$軸に関して$(a,b)$と対称な点
- 確率$\dfrac13$で$y$軸に関して$(a,b)$と対称な点
- 確率$\dfrac16$で直線$y=x$に関して$(a,b)$と対称な点
- 確率$\dfrac16$で直線$y=-x$に関して$(a,b)$と対称な点
にいる.
以下の問いに答えよ. ただし, (1)については, 結論のみを書けばよい.
(1)$\mathrm{P}$がとりうる点の座標をすべて求めよ.
(2) $n$を正の整数とする. 最初から$n$秒後に$\mathrm{P}$が点$(2,1)$にいる確率と, 最初から$n$秒後に$\mathrm{P}$が点$(-2,-1)$にいる確率は等しいことを示せ.
(3) $n$を正の整数とする. 最初から$n$秒後に$\mathrm{P}$が点$(2,1)$にいる確率を求めよ.
長いですね. 図にすると以下のようになります.

上図の8つの点((1)で聞かれているのがこれです)を点$\mathrm{P}$が動き, その動きは4つのうちから1つの軸を選びそれに関して反転させるというものです.
${}$
まず頭の中で何回か操作をしてみると, いろいろな対称性があることがわかります. 具体的には,
- $x$軸または$y$軸を選び続けると, 特定の4点しか通らない.
- $y=x$または$y=-x$を選び続けても, 特定の4点しか通らない.
- 奇数回の操作後, 偶数回の操作後では, それぞれ特定の4点にしかいることはない.(ななめの正方形が浮かび上がってきます.)
などでしょうか.
${}$
さて, 大学数学では, 「対称性を記述する」と言われる理論があります. それが群論です.
状況を抽象化する
このままでは若干分かりにくいので, 今回の問題の本質を抽出していきましょう.
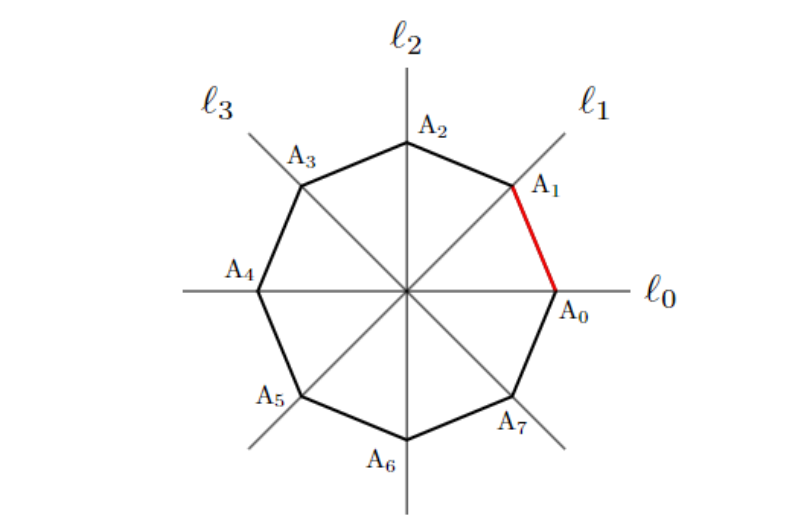
まず, 8つの点が成す8角形は正8角形としてしまって問題なく, その方が対称性が分かりやすくなります. また, 頂点が軸上にあった方が何かと都合が良いので, 次のように図を描きかえてしまいましょう.

ここで, 点$(2,1)$は$\ell_0$と$\ell_1$の間にあったので, この図では辺$\mathrm{A}_0\mathrm{A}_1$が対応することに注意します.
すると元の問題は次のように書き換えられます.
「正8角形$\mathrm{A}_0\mathrm{A}_1\cdots \mathrm{A}_7 $ を, $\ell_0~\ell_3$のどれかに関して反転させる」という操作を$n$回繰り返したとき, 赤く塗った辺$\mathrm{A}_0\mathrm{A}_1$が元の位置に戻ってくる確率を求めよ.
${}$
このような, ある対象に対する(可逆な)操作の合成がどのように振る舞うか, を数式で表現するのが群論となります. (正確にはこれは群の作用ですが.)
群論(二面体群)を知らない方は以下をクリックして簡単な説明を読んでください.
群論の簡単な説明(クリックして開く)
まず, 「4つの軸による反転」という操作を, もっと簡単な操作で表せないかと考えてみます.
例えば, 「$\ell_0$で反転した後, $\ell_1$で反転する」という操作を考えてみてください. この合成はどのような操作になるでしょうか?
 (再掲)
(再掲)
そう, 実はこれは「90°回転する」という操作になっているのです!
そこで, 4つの軸による反転は, 「$\ell_0$による反転」と「回転」の2種類の操作の合成だけで表せるのではないか?と考えられます. 実際これは正しいです.
${}$
それでは, これを数式で表すことを考えてみましょう. 正8角形の全体を変えずに点のみを動かす操作として最も単純なものとして,
・「$\ell_0$による反転」を$t$
・「45°回転」を$r$
と表すことにしましょう.
さらに,
・操作の合成を積で表すことにします. つまり, 例えば「$\ell_0$で反転した後に90°回転」という操作は$tr^2$と表されます.
・逆の操作を, 逆数のように肩に$-1$を付けて表すことにします. つまり例えば「-45°回転した後に$\ell_0$で反転」という操作は$r^{-1}t$と表されます.
・「何もしない」という操作を$1$で表すことにします. すると, $t^2=1,\ r^8=1$が成り立ちます.
ここで注意は, $rt\neq tr$であるということです. 実際, 以下の図のようになります.
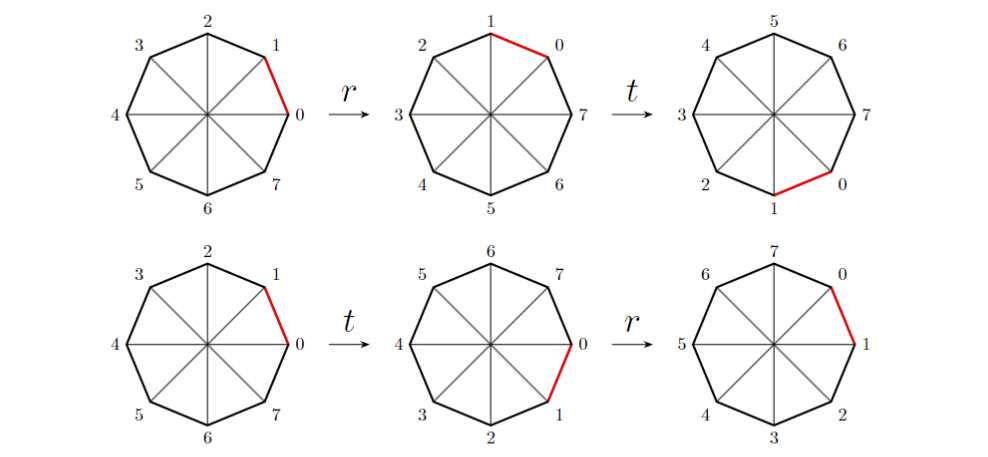
このように, 通常の積と違って交換法則が成り立たないことに注意してください. 上の図をよく見ると, 正しくは$rt$と, $tr$をさらに-90°回転したものが等しい, 即ち$rt=tr^{-1}$が成り立つことが分かります.
この関係式を使うことで, 例えば
$trtr^2tr^3=t\cdot tr^{-1}\cdot r^2tr^3=rtr^3=tr^{-1}\cdot r^3=tr^2$
のように簡約化ができます. 従ってこのように$r$を右に動かしていくことにより, 正8角形に対する「全ての操作の集合」は
$\{1, r, r^2, \ldots, r^7, t, tr, tr^2, \ldots, tr^7\}$
の合計16個になることが分かります.
このような操作の集合とそれらの合成による関係性を合わせて, 二面体群といって$D_8$と表します.(もちろん正$n$角形に対する操作の場合$D_n$となります. )
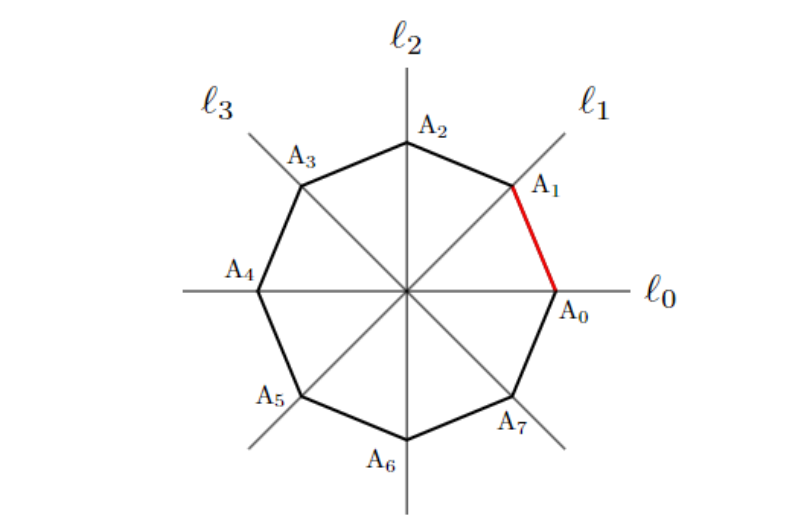
それでは最後に, 4つの軸$\ell_0~\ell_3$に関する反転を$r$と$t$で表してみましょう.
 (再掲)
(再掲)
$\ell_1$に関する反転は, 「-45°回転し, 上下反転し, 45°回転する」という操作により作ることができます. 従ってこれは,
$r^{-1}tr=r^{-1}\cdot tr^{-1}\cdot r^2=tr^2$
より$tr^2$と表すことができます!
そうすると, 初めに書いた「$\ell_0$で反転した後$\ell_1$で反転」=「90°回転」というのも, $t\cdot tr^2=r^2$から簡単にわかってしまいます.
同様に考えると, $\ell_i\ (i=0,1,2,3)$に関する反転は$tr^{2i}$となることが分かります.
${}$
群を考える
ということで, 二面体群
$D_8=\{t^nr^m\ |\ t^2=r^8=1, rt=tr^{-1}\}$
において, $\ell_i$に関する反転$r^{-i}tr^i=tr^{2i}$たちの積が, 赤く塗った辺$\mathrm{A}_0\mathrm{A}_1$を動かさない操作になる条件, つまり積が$1$または$tr$に等しくなるような条件を考えていきましょう.
ところが, $tr^{2i}$の積しか考えないので$tr$に等しくなることはありえません!さらに$r^2$を改めて$r$と書いてしまうことで, $D_4$における以下のような問題に書き換えられます.
これは群論の言葉で言うと, $D_8$の, $tr^{2i}\ (i=0,1,2,3)$により生成される部分群が$D_4$と同型なのでそこで考えて行く, ということです.
$D_4=\{t^nr^m\ |\ t^2=r^4=1, rt=tr^{-1}\}$ において, $x_i=tr^i\ (i=0,1,2,3)$とおく.
| $x_0$ | $x_1$ | $x_2$ | $x_3$ |
|---|---|---|---|
| $\tfrac13$ | $\tfrac16$ | $\tfrac13$ | $\tfrac16$ |
の確率に従って$x_i$を$n$回選んだとき, それらの積が$1$となる確率を求めよ.
${}$
さて, $tr^i$たちの積を考えたいのですが, この積は交換できないので, 回数だけでなく出た順番まで考慮しないといけなくてちょっと難しそうです. そこで, modをとって単純化することを考えてみます!
${}$
群論を知っている方向けの説明(クリックして開く)
$D_4$は位数8ですが, 一般に位数$p^2$の群はAbel群( 龍孫江さんの動画 などを参照)なので, $D_4$を位数2の正規部分群で割ると商がAbel群になりうまく行きそうな気がしてきます. ところが, $D_4$の位数2の正規部分群は$\langle r^2\rangle$しかありません!
剰余群$D_4/\langle r^2\rangle$は位数4のAbel群で明らかに巡回群ではないので, $D_4/\langle r^2\rangle\cong(\mathbb{Z}/2\mathbb{Z})^2$が分かります.
記号の濫用ですが$r,t$の商による像も$r,t$で表し, $D_4/\langle r^2\rangle=\{1,r,t,tr\ |\ r^2=t^2=1, rt=tr\} $と書くことにします.
${}$
群論を知らない方向けの説明(クリックして開く)
群におけるmodとして, 剰余群という概念があります. 今回は, 「$r$のベキをmod2する」ことを考えてみましょう.
通常のmod2とは「差が2の倍数である2数を同一視する」というものでしたから, 今回は「$xy^{-1}$が$r^{\text{2の倍数}}$であるような$x$と$y$を同一視する」ことを考えます. このようにして新しく得られた群を$D_4/\langle r^2\rangle$と書きます.
具体的に書くと, $D_4=\{1, r, r^2, r^3, t, tr, tr^2, tr^3\}$であったところが$r=r^3$や$t=tr^2 $などとなり, $D_4/\langle r^2\rangle=\{1,r, t, tr\}$となります.
するとこの世界では, $rt=tr^{-1}=tr$となり, 積が交換可能になるのです!
※ただし実際には, 一般の群ではどんなmodでも考えられるわけではなく, 同一視する部分が「正規部分群」と呼ばれる特別な性質を持っている必要があります. 今回の$\langle r^2\rangle=\{1,r^2\}$は実は正規部分群になっています. さらに, 位数(=要素数)が2の, 「あまり潰さない」正規部分群は, 実はこれに限られるのです!
${}$
剰余群で考える
これで$D_4/\langle r^2\rangle$での考察に移れるのですが, ここでは$1$と$r^2$は同一視されているので, 積が$1$となる確率だけを求めることはできなくなってしまいます.
しかし!実は...(クリックして開く)
| $x_0$ | $x_1$ | $x_2$ | $x_3$ |
| $\tfrac13$ | $\tfrac16$ | $\tfrac13$ | $\tfrac16$ |
この表で, $x_0$と$x_2$, $x_1$と$x_3$の確率が等しくなっていることがここで効いてきます. $D_4$において$x_{i_0}x_{i_1}\cdots x_{i_n}=r^2$となっているとき, $x_{i_n}=x_0$ならそれを$x_2$に, $x_{i_n}=x_1$ならそれを$x_3$に, 変えたものを考えると, 確率は変わらず積は$1$になるのです!
従って, $n$個の$x_i$たちの積が$1$になる確率と$r^2$になる確率は等しいことがわかります! これが元々の問題の(2)に対応しています.
${}$
すると, さらに以下のような問題に書き換えられることになります.
$D_4/\langle r^2\rangle=\{1,r, t, tr\}$において, $x_0=x_2=t$, $x_1=x_3=tr$をそれぞれ確率$\tfrac23,\tfrac13$で選ぶことを$n$回繰り返すとき, それらの積が$1$となる確率の$\tfrac12$倍の値を求めよ.
${}$
ここまで来ると, 積は可換ですから結局「$t,r$をどちらも偶数回ずつ掛ける」確率を求めれば良いことになりますね. (積が可換なので, 選ぶ順番を気にせず回数だけ考えればよくなったところがポイント.)
これは, $t,r$を変数$x,y$と対応させて
$f(x,y)=\left(\frac23 x+\frac13 xy\right)^n=x^n\left(\frac23 +\frac13 y\right)^n$ を展開したときの, $x^{\text{偶数}}y^{\text{偶数}}$の係数の和
の$\frac12$倍と等しくなります.(展開したときにどのように選んで掛け合わされるか考えてみてください!)
${}$
これは, まず$x^n$の方を見ることで$n$が奇数なら$0$であることが分かります. そして$n$が偶数のときは$\frac{f(1,1)+f(1,-1)}{2}$によって$y^{\text{偶数}}$の係数の和を求められますから, 答えは
$ p_n=\begin{cases}\dfrac14\left(1+\Big(\dfrac13\Big)^n\right) &(n\text{:偶数})\\[5pt] 0 &(n\text{:奇数})\end{cases}$
と求めることができます.
${}$
おわりに
こう見てみると, 元々の(2)の誘導が本質的なものだったということになりますね. 2つを同一視することにより操作の合成を簡単に捉えることができるようになります. この発想を, 群論を用いて「剰余群」として説明付けられるのはとても面白いですね.
お楽しみいただけたでしょうか. これを読んで群論に興味を持ってもらえたら幸いです.
${}$
群環と表現論による解法
実はもうちょっとだけ続きます. ただしこの後は私があまり詳しくない分野を用いますので, お話程度に読んでいただけると幸いです.
${}$
上で用いた解法は, 母関数を用いるためには「順番は気にせず回数のみを考えれば良い状況」、即ち変数の積が可換である必要があったため, $D_4$のままではだめでさらにその剰余群を考えたのでした.
しかし, 群の元を変数とした係数つきの形式和, と言えば群環ではないですか!群環で母関数を考えることにより, 上記の問題を解決することができます.
${}$
具体的には, 群環$\mathbb{C}[D_4]$とは, $D_4$の8つの元を基底, 係数を$\mathbb{C}$とするベクトル空間に, 積を群での積によって定めて得られる環です. つまり,
$(2+3tr)(r-2t)=2r+3tr^2-4t-6trt=2r-6r^3-4t+3tr^2$
のように積が入った, 群の元の係数つき形式和の環です.
すると, 上述の
$D_4=\{t^nr^m\ |\ t^2=r^4=1, rt=tr^{-1}\}$ において, $x_i=tr^i\ (i=0,1,2,3)$とおく.
| $x_0$ | $x_1$ | $x_2$ | $x_3$ |
|---|---|---|---|
| $\tfrac13$ | $\tfrac16$ | $\tfrac13$ | $\tfrac16$ |
の確率に従って$x_i$を$n$回選んだとき, それらの積が$1$となる確率を求めよ.
この問題は, 次のように書き換えられます.
$\mathbb{C}[D_4]$において, $\left(\frac13t+\frac16tr+\frac13tr^2+\frac16tr^3\right)^n$を展開したときの, $1$の係数を求めよ.
すごく簡単になりましたね. さらに, 表現論の一般論で有限群$G$に対し$\mathbb{C}[G]$は$\mathbb{C}$係数行列環の直積と同型になることが知られているので, あとは同型が具体的に分かれば$n$乗も簡単に計算できます.
${}$
と, ここまで来て私には手に負えなくなってしまったので友人の げの くんに助けを求めたところ,
事実:$\mathbb{C}[G]\cong \mathbb{C}^4\times M_2(\mathbb{C})$で, 同型は$t^nr^m\mapsto \left(1, (-1)^n, (-1)^m, (-1)^{n+m}, \begin{pmatrix}0&1\\1&0\end{pmatrix}^n\begin{pmatrix}i&0\\0&-i\end{pmatrix}^m\right)$ により定まるもので与えられることが知られている.
と教えてもらったので, これを使ってみます. (勉強しないといけません.)
${}$
これによる$\frac13t+\frac16tr+\frac13tr^2+\frac16tr^3$の行先を頑張って計算してみると, なんと$\left(1, \frac13, -1, -\frac13, O\right)$となり, 行列の部分が0になりました!従ってこれの$n$乗は$\left(1, (\frac13)^n, (-1)^n, (-\frac13)^n, O\right)$であり, これを$\mathbb{C}[G]$に戻したときの$1$の係数が分かれば良いです.
ところがこの同型の逆写像を与える式が知られていて, こちらの記事 のように有限群のFourier逆変換と呼ばれるもので, これを用いることで
$ \begin{align*} p_n &=\frac18\left(1+\Big(\frac13\Big)^n+(-1)^n+\Big(\!\!-\frac13\Big)^n\right)\\[5pt] &=\frac18\left(1+(-1)^n\right)\left(1+\Big(\frac13\Big)^n\right)\\[5pt] &=\begin{cases}\dfrac14\left(1+\Big(\dfrac13\Big)^n\right) &(n\text{:偶数})\\[5pt] 0 &(n\text{:奇数})\end{cases} \end{align*} $
と求めることができました.
東大入試が表現論を使って解けるなんてびっくりですね!
${}$
おわりに
この考え方を使うと, 普段の母関数の, 代入して足して係数を求めるというやつも, 上のFourier逆変換で説明することができそうです.
また, 今回のように群を割ることによって群環を簡単にする, という手法に一般論はあるのか, などいろいろと疑問が湧きました.
いつかこの辺をきちんと勉強してまとめなおせたら良いなと思います.
それでは, 最後まで読んでくださった方, ありがとうございました.
