major indexによるq-Narayana数とq-Catalan数
概要
Catalan数に関係する数として
Narayana数
\begin{align}
N_{n,k}\triangleq\frac{1}{n}\binom{n}{k}\binom{n}{k-1}
\end{align}
がある．Narayana数はピークを$k$個持つ，サイズ$n$のDyck路の数に等しい．
またここから，Narayana数の$k$にわたる和は，Catalan数であることがわかる．
本稿ではNarayana数の$q$類似を解説する．
Dyck路にmajor indexという統計量を入れて数え上げると，母関数として$q$-Narayana数
\begin{align}
N_{n,k}(q)=\frac{q^{n+k(k-1)}}{[n]_q}\binom{n}{k}_q\binom{n}{k-1}_q
\end{align}
が出てきて，さらにその和は$q$-Catalan数
\begin{align}
C_n(q)\triangleq \frac{q^n}{[n+1]_q}\binom{2n}{n}_q
\end{align}
になることが知られている [1]．
準備
二種のステップ$\mathsf{A}\triangleq(1,0),\mathsf{B}\triangleq(0,1)$を使って$(0,0)$から$(n,n)$まで行くパスのうち，直線$y=x$より上に行かないものをDyck路という．
Dyck路は，
以前の記事
[5]で紹介した正方格子路の一種である．$(0,0)$から$(n,n)$へ行くDyck路の集合を$\textrm{Dyck}(n)$と書く．
例えば下図は$\textrm{Dyck}(5)$の元の例．
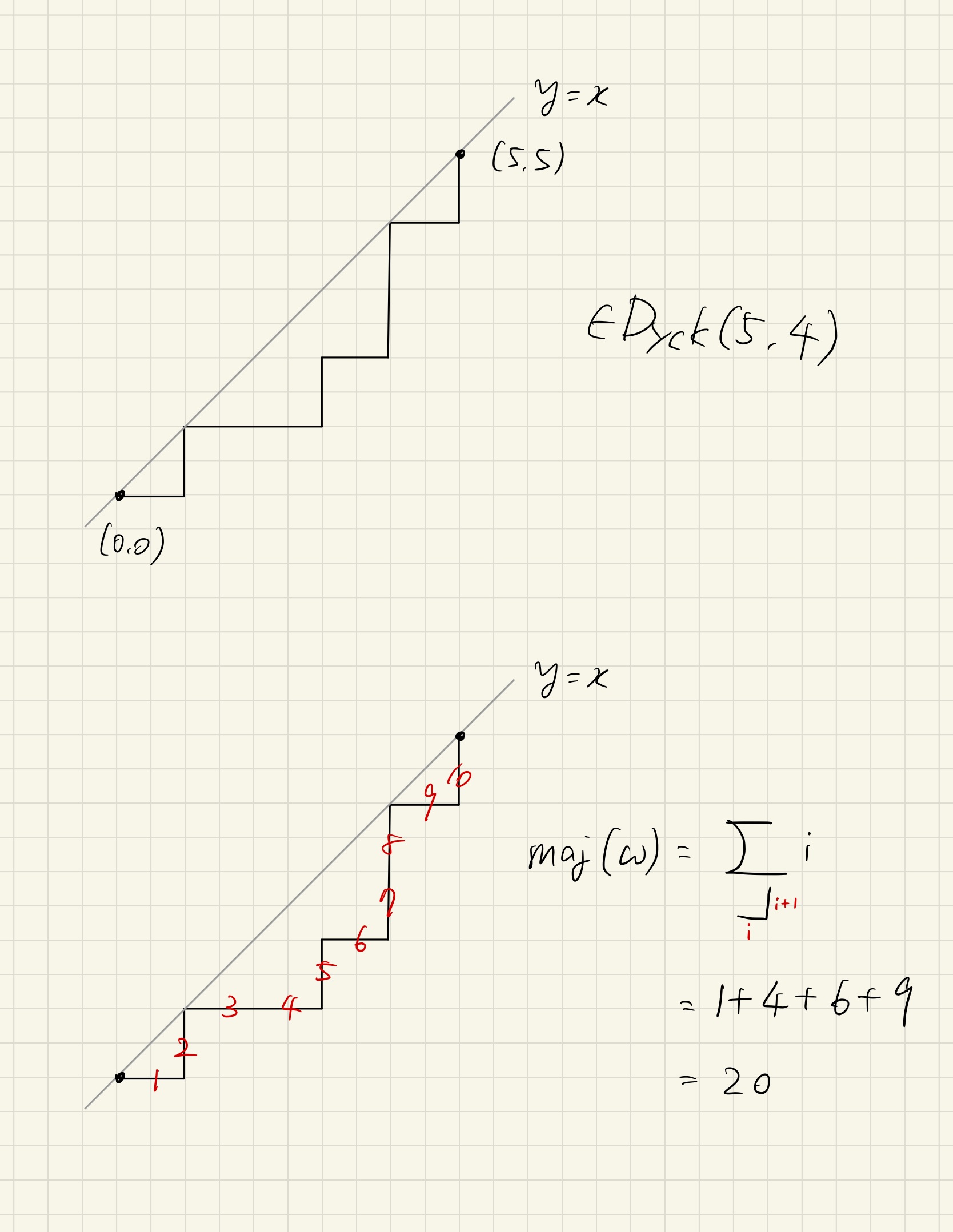Dyck路の例と，そのmajの値
major indexについて復習
集合$\textrm{Dyck}(n)$から自然数への写像
\begin{align}
\textrm{maj}\colon\textrm{Dyck}(n)\to\mathbb{N}
\end{align}
を，以前の記事 [5]で定めたように定義する．復習すると，Dyck路
\begin{align}
\omega=\omega_1\cdots\omega_{2n},\qquad \omega_i\in\{\mathsf{A,B}\}
\end{align}
に対して，descentと呼ばれる集合$D(\omega)$を
\begin{align}
D(\omega)\triangleq\{i\mid \omega_i=\mathsf{A},\ \omega_{i+1}=\mathsf{B}\}
\end{align}
と定め，その和
\begin{align}
\textrm{maj}(\omega)\triangleq\sum_{i\in D(\omega)}i
\end{align}
をmajor indexと呼ぶのであった．
上の図の例でいうと，パスの中で"┘"みたいになってる場所がdescentである．
descentの数ごとのDyck路の数え上げ
descentの要素数が$k$個であるようなDyck路の集合を
\begin{align}
\textrm{Dyck}(n,k)\triangleq\{\omega\in\textrm{Dyck}(n)\mid\#D(\omega)=k\}
\end{align}
とかく．
この集合をmajor indexに関して数え上げる母関数を
\begin{align}
N_{n,k}(q)\triangleq\sum_{\omega\in \textrm{Dyck}(n,k)}q^{\textrm{maj}(\omega)}
\end{align}
とかき，$q$-Narayana数という．
$q$-Narayana数の積表示
まず，$q$-Narayana数は以下のようにSchur関数の特殊値である．
\begin{align}
N_{n,k}(q)=q^ns_{\langle 2^{k-1}\rangle}(q,q^2,\ldots,q^{n-1})
\end{align}
が成り立つ．但し，$s$はSchur関数を表し，$\langle2^{k-1}\rangle$は縦が$k-1$で横が$2$の長方形のヤング図形を表す．
Dyck路からparallelogram polyomino (staircase polygonとも呼ばれる)への全単射を考える [4]．
サイズ$n$で$k$列のparallelogram polyomino (略してポリオミノ)とは，$(0,0)$から$(k,n+1-k)$へ，ステップ$\mathsf{A,B}$を使って行く二本のパスの組で，$(0,0)$と$(k,n+1-k)$以外では交差しないものである．
サイズ$n$で$k$列のポリオミノの集合と，集合$\textrm{Dyck}(n,k)$の間に一対一対応が存在する (下図)．
Dyck路ポリオミノの一対一対応
この全単射の正確な定義は文献 [4,Exercises 57]に任せるとして，めっちゃ雑に説明すると，Dyck路のステップ$\mathsf{A}$ (下図でいうと➘)の情報がポリオミノの「上の線（図の赤い線）」で表され，$\mathsf{B}$ (図でいうと➚)の情報が「下の線（図の青い線）」で表されるのである．（下図参照）
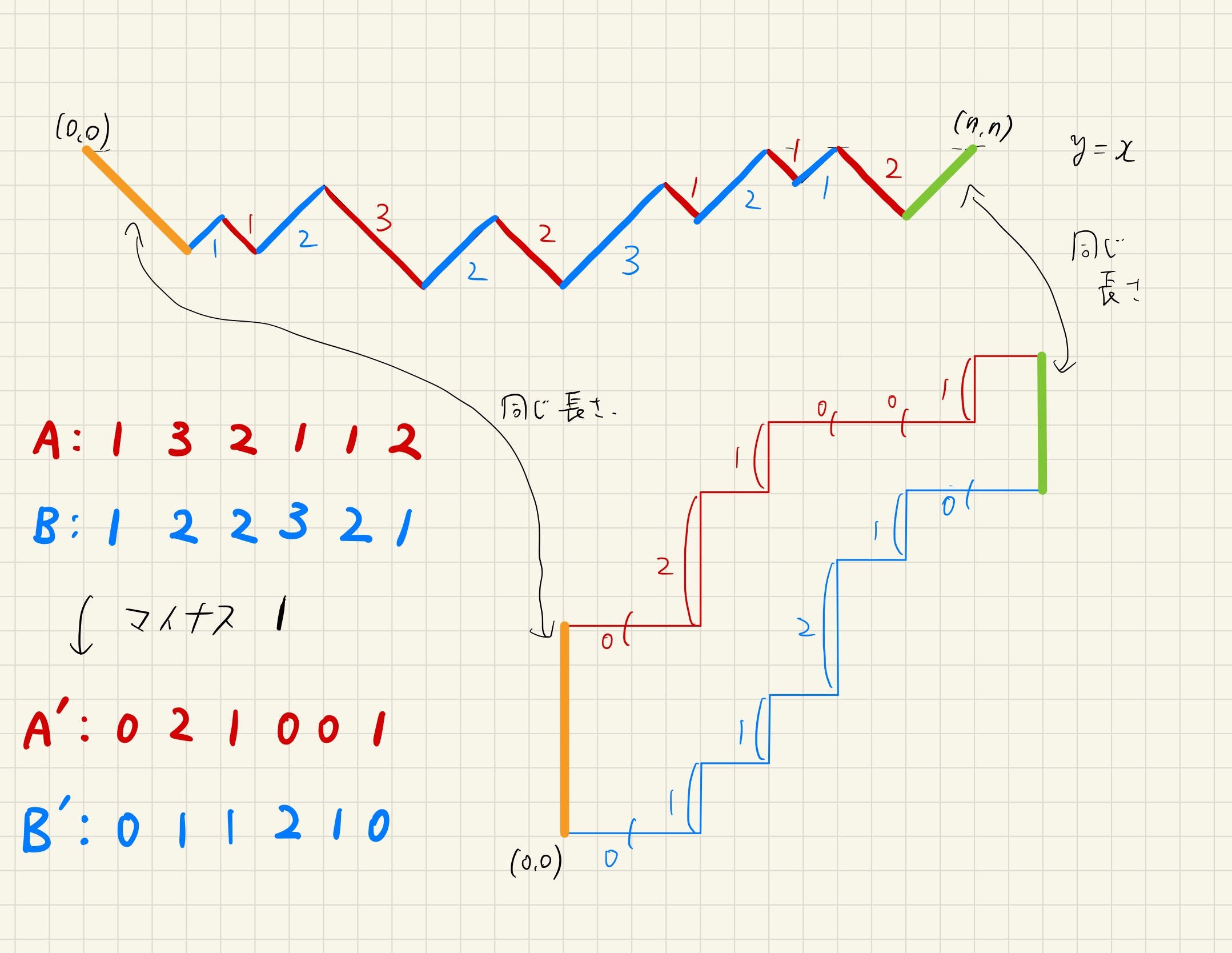全単射のめっちゃ雑な説明
この全単射を曇りなき眼で見ると，重みを入れることができる．
つまり，ポリオミノが置かれているグリッドの横線 (ステップ$\mathsf{B}$)に下図下側のように重みを入れると，ポリオミノが通る横線の重みの積が，Dyck路のmajor indexに一致する．
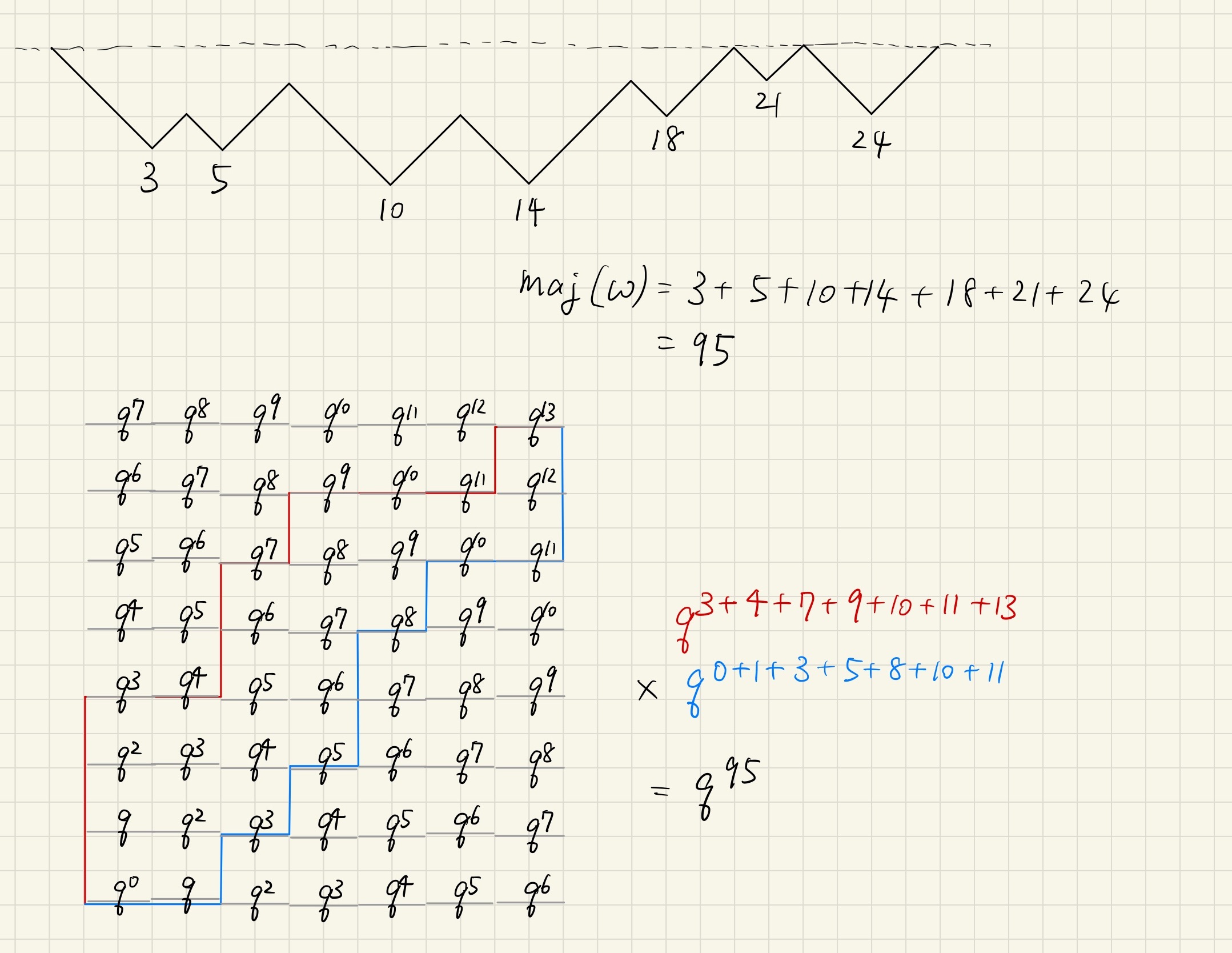major indexと，横線の重みの積が一致する様子
つまり，$q$-Narayana数$N_{n,k}(q)$は，サイズ$n$で$k$列のポリオミノを，上図の重みのもとで数え上げる母関数に一致する．
ここで，
Lindström–Gessel–Viennotの補題
を使うと，その母関数は基本対称式の行列式として
\begin{align}
N_{n,k}(q)=q^n\det\left[\begin{array}{ll}e_{k-1}(q,\ldots,q^{n-1})&e_k(q,\ldots,q^{n-1})\\e_{k-2}(q,\ldots,q^{n-1})&e_{k-1}(q,\ldots,q^{n-1})\end{array}\right]
\end{align}
と表せて，Jacobi-Trudi公式 (
Nägelsbach–Kostka恒等式
ともいうらしい)を使うとそれはSchur関数を使って
\begin{align}
N_{n,k}(q)=q^ns_{\langle 2^{k-1}\rangle}(q,q^2,\ldots,q^{n-1})
\end{align}
と書ける．
上の定理で求めた式は以下の通り計算できて積型になる．
\begin{align}
N_{n,k}(q)&=q^ns_{\langle 2^{k-1}\rangle}(q,q^2,\ldots,q^{n-1})\\
&=\frac{q^{n+k(k-1)}}{[n]_q}\binom{n}{k}_q\binom{n}{k-1}_q
\end{align}
やることはWeylの指標公式
\begin{align}
s_\lambda(x_1,\ldots,x_n)=\frac{\det(x_i^{\lambda_j+n-j})_{i,j=1}^n}{\det(x_i^{n-j})_{i,j}^n}
\end{align}
に突っ込んで，右辺のVandermonde行列式を計算するだけなのだが，特にヤング図形が長方形のときは計算した結果がすでに平面分割のMacMahon公式
\begin{align}
s_{\langle t^r\rangle}(q,q^2,\ldots,q^{r+s})=q^{r(r-1)t/2}\prod_{i=1}^r\prod_{j=1}^s\prod_{k=1}^t\frac{1-q^{i+j+k-1}}{1-q^{i+j+k-2}}
\end{align}
として知られているから，ここでは簡単のためそちらを使う．
突っ込んで計算するだけなのであとは省略する．
Weylの指標公式とかMacMahon公式とかに関しては，文献 [3] が詳しいので，そちらを見ると良い．
$q$-Catalan数の積表示
$q$-Narayana数の$k$にわたる和
\begin{align}
C_n(q)\triangleq\sum_{k=1}^{n-1}N_{n,k}(q)
\end{align}
を$q$-Catalan数という．
\begin{align} C_n(q)= \frac{q^n}{[n+1]_q}\binom{2n}{n}_q \end{align}
Heineの和公式
[2]
\begin{align}
_2\phi_1(q^{-n},b;c;q,cq^n/b)=\frac{(c/b;q)_n}{(c;q)_n}
\end{align}
を使う．
\begin{align}
\sum_{k=1}^nN_{n,k}(q)
&=\sum_{k=1}^n\frac{q^{n+k(k-1)}}{[n]}\binom{n}{k}_q\binom{n}{k-1}_q\\
&=q^n\cdot_2\phi_1(q^{-n+1},q^{-n};q^2;q,q^{2n+1})\\
&=q^n\frac{(q^{n+2};q)_{n-1}}{(q^2;q)_{n-1}}\\
&=\frac{q^n}{[n+1]_q}\binom{2n}{n}_q
\end{align}
