石鹸膜の幾何学入門(0): 極小曲面論入門

Introduction

子供の頃に誰もが遊んだことがあるであろうシャボン玉. 針金やプラスチックでできた枠をシャボン液に浸して引き上げると, その枠を石鹸膜が張るのが見て取れます. 石鹸膜の張る曲面は極小曲面と呼ばれ, その研究の起源はLagrangeの時代にまで遡ります. 彼が提唱した「閉曲線を張る極小曲面の存在性」を問うPlateau問題の解決により, Douglasが第1回Firlds賞受賞者に選ばれたことは有名です.

石鹸膜の張る極小曲面
19世紀に入り, 極小曲面を局所的に正則関数の積分として表示する表現公式がEnneperとWeierstrassによって独立に発見されてからは, 複素解析的アプローチで極小曲面の理論が整備されていきました. 20世紀以降も彼らの表現公式の威力は健在で, Riemann面の理論を援用して豊富な具体例が構成されていきました. 一方, この頃同時に発展していた関数解析や測度論を用いた実解析的アプローチにより, 極小曲面を含めた一般の幾何学的変分問題の解の存在性や正則性, そして解の安定性の研究が推し進められていきます.

現在もなお, 極小曲面は変分問題の基本的かつ主要なトピックのひとつとして研究され続けています.

本シリーズでは, 次の定理の証明を一旦の最終目標に据え, 現代的な極小曲面論のイントロ部分を解説しようと思います.

前提知識

以下に示すような各種幾何学の基礎的な事柄について知っていれば十分理解できる内容にしようと考えています. (学部2~3年程度?)

• 曲面論: 第一・第二基本形式, Gauss曲率, 平均曲率.
• ベクトル解析: 勾配, 発散, ラプラシアン.
• 多様体論: はめ込み, 発散定理(Stokesの定理).
• Riemann幾何学: 接続, 測地線, (測地的)完備性.

全体を通してなるべくself-containedな内容になるように心がけます.

文献の紹介

本シリーズでは, ColdingとMinicozziによる, 幾何解析(≒Riemann多様体上の偏微分方程式論)的手法を用いた現代的な極小曲面論の教科書CMのChapter1に沿って解説をしていきます. 極小曲面論の古典的名著としてはOssermanによるOssがあります. こちらは複素解析や曲面論の延長として読めるので, より気軽にこの分野について学べます(あと, お手頃価格です).

現在(2024年4月)入手しやすい日本語の極小曲面の教科書としては, 宮岡氏によるMiがあります. Ossermanの教科書の現代版といった雰囲気で, 理論的内容はもちろん, 具体例の構成やその計算例の豊富さが魅力です. また, 小磯氏による pdf Koは誰でも閲覧可能で, 日本語の文献としては珍しく極小曲面の安定性についても触れられています.

色々な極小曲面の具体例が見られるサイトとしては, 藤森氏 と Weber のページがあります.

石鹸膜と変分問題

石鹸膜のかたち

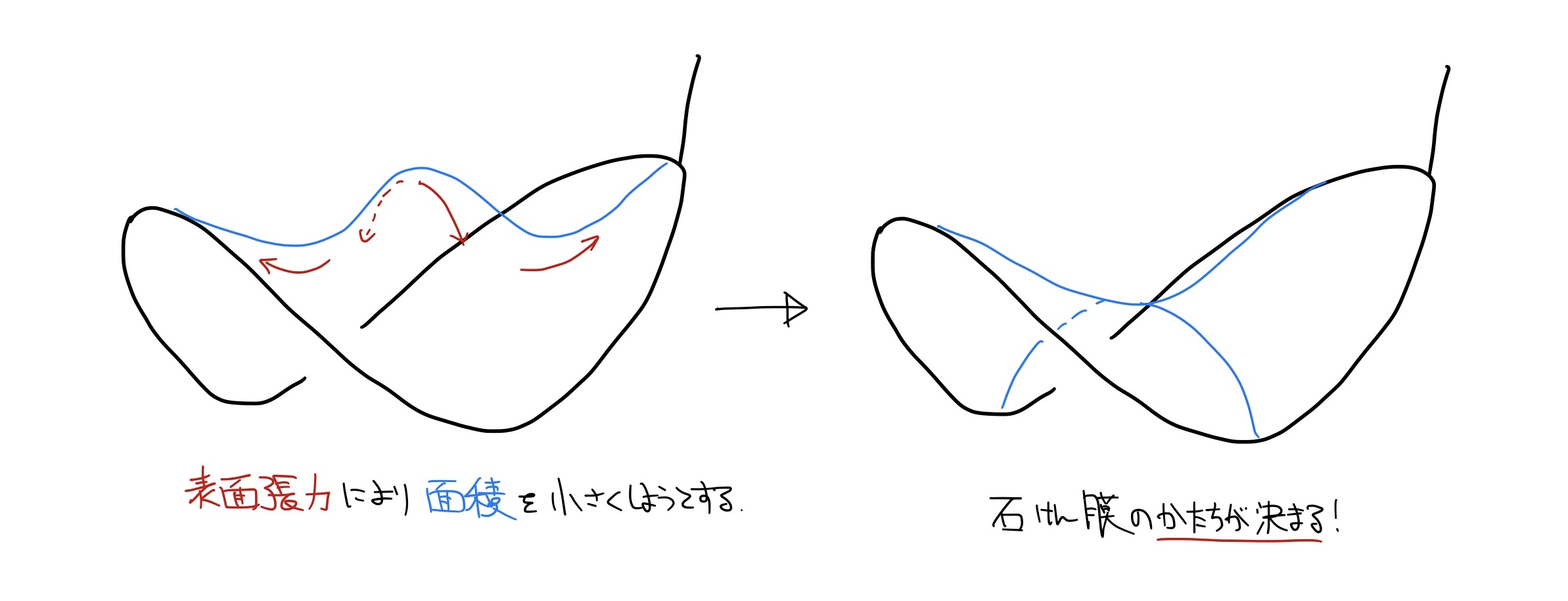
本論に入る前に, 石鹸膜の張る曲面のかたちはどのようにして決まるのかについてざっくりと説明します(当方界面の物理学の専門家ではないので本当にざっくりです).

シャボン液から引き上げられ空間に置かれた石鹸膜は, その周りを空気という別の物質で取り囲まれることになります. 空気と石鹸膜のように異なる物質間の境界(=界面)には, その境界面に沿う方向に表面張力が働きます. 石鹸膜は非常に薄く軽いため, 重力の影響を無視することにすると, 石鹸膜に働く表面張力による(自由)エネルギーはその表面積に比例します. 物理的に平衡な状態は, そのエネルギーをなるべく小さくしようとした結果として実現されるので, 石鹸膜は自身の表面積をなるべく小さくするよう変形し, その結果として最終的な曲面のかたちが決定します.
枠を張る石鹸膜形成のイメージ
数学的に以上のことをまとめると, 石鹸膜は面積汎関数の臨界点(="微分"が$0$になる点)としてモデル化されることになります. 実際に物理的に実現可能なのは, 臨界点の中でも局所的に最小, すなわち面積汎関数の極小点になる場合です. これが極小曲面の名前の由来です.

シャボン玉についても同様の原理でそのかたちが決定されますが, あちらは追加で石鹸膜が囲む空気(領域)の体積が一定という制約条件のもとで表面積を極小化しています(こちらもいつか記事にしたいと考えています).

変分法のイメージ

石鹸膜のかたちが「面積を極小化」するように決まることがわかったところで, 我々が普段どのようにして何かの量の最小値を求めていたか思い出してみましょう. 高校数学では, 関数の最大・最小値を求める際に, 関数の微分が$0$になる点を探していました. 関数が最小となるための必要条件が微分が$0$になることだったからです.
微分が$0$になる点が極小点の候補

同じことを汎関数に対してもやってみようというのが変分法です.

変分法では, 与えられた曲面$\Sigma$を微小変形した族$\Sigma_t$を考え, それらの面積$\area{\Sigma_t}$をパラメータ$t$について微分します.　これがなぜ面積を「微分」したことになるのかは, 面積を「曲面全体のなす"空間"上の関数」と捉えるとわかりやすいです. 曲面$\Sigma$の微小変形$\Sigma_t$はこの"空間"上の曲線と考えられますので, 面積のパラメータ$t$に関する微分は, 面積をこの曲線の接方向に微分したのと同じことだと考えられます. これは状況的には, 多様体上の微分の定義とほとんど同じものになっています. すなわち変分は, 曲面全体のなす無限次元の空間上の微分法とでも呼ぶべきものと言えるでしょう.

よって, 面積の極小点(臨界点)を見つけるためには, どんな微小変形に関する変分も$0$になるような条件を求めてやれば良いわけです.
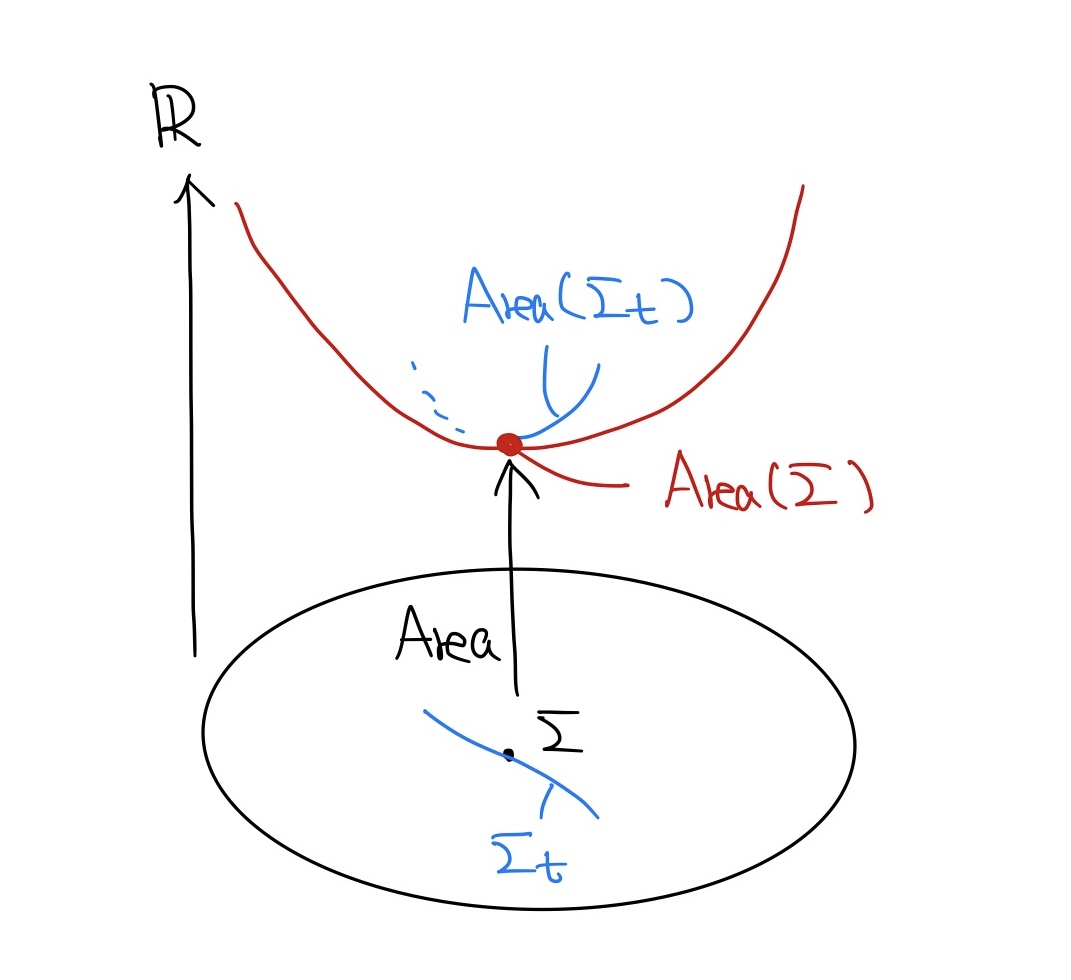曲面全体のなす"空間"上の汎函数としての面積

練習: グラフの表面積を変分しよう

最後に, より具体的に変分法の雰囲気を掴んでいただくため, 領域上の関数のグラフの面積の変分を計算してみることにします. $u$を有界領域$\Omega \subset \mbb{R}^2$上の$C^2$関数で, 境界も込めて連続なものとすると, $u$のグラフ$\Sigma = \{(x, y, u(x, y)) | (x, y)\in \Omega\}$の面積は
\begin{align} \area{\Sigma} &= \int_{\Omega} |(1, 0, u_x)\times (0, 1, u_y)|dxdy \\ &= \int_{\Omega}\sqrt{1+u_x^2+u_y^2}dxdy = \int_{\Omega}\sqrt{1+|\nabla u|^2}dxdy \end{align}
となります. $\phi \in C_0^1(\Omega)$を任意にとり, $u$を微小変形させた関数$u+t\phi$のグラフ$\Sigma_t$の面積を考えると, 上と同様にして
\begin{align} \area{\Sigma_t} = \int_{\Omega}\sqrt{1+|\nabla u + t\nabla \phi|^2}dxdy \end{align}
となります.
\begin{align} |\nabla u + t\nabla \phi|^2=|\nabla u|^2+2t\inn{\nabla u}{\nabla \phi}+t^2|\nabla \phi|^2 \end{align}
に注意すると, この変形のパラメータ$t$に関する微分は
\begin{align} \left.\frac{d}{dt}\right|_{t=0}\area{\Sigma_t}=\int_{\Omega} \frac{\inn{\nabla u}{\nabla \phi}}{\sqrt{1+|\nabla u|^2}}dxdy \end{align}
と計算できます. ここで,
\begin{align} \div{\phi \frac{\nabla u}{\sqrt{1+|\nabla u|^2}}} = \phi\, \div{\frac{\nabla u}{\sqrt{1+|\nabla u|^2}}}+ \frac{\inn{\nabla u}{\nabla \phi}}{\sqrt{1+|\nabla u|^2}} \end{align}
であり, $\phi$は$\partial \Omega$上で$0$になることにも注意すると, 発散定理より
\begin{align} \left.\frac{d}{dt}\right|_{t=0}\area{\Sigma_t}= -\int_{\Omega}\phi\, \div{\frac{\nabla u}{\sqrt{1+|\nabla u|^2}}}dxdy \end{align}
となります.
ここで, 次の有名な事実を使います(証明は次回以降に行います).

変分法の基本補題を用いると, $\phi$の任意性から,
「面積$\area{\Sigma}$の変分が$0$」 $\iff$ 「$u$は方程式$\displaystyle \div{\frac{\nabla u}{\sqrt{1+|\nabla u|^2}}}=0$を満たす」
がわかります. $u$の満たすこの偏微分方程式は極小曲面方程式と呼ばれます.

極小曲面の研究は, ある種の偏微分方程式の解の幾何学的な研究と見ることもできます.

おわりに

今回は石鹸膜の幾何学の概要や, なぜ変分を考えるか等の雰囲気を紹介しました.
次回 は本格的な変分計算のための, 曲面論の復習を行おうと思います.