文献あり

HGP符号の話

量子エラー訂正符号,physlab2026アドベントカレンダー

0. はじめに

　こんにちは。今回はPhysics Labアドベントカレンダーの一環として、Hypergraph Product code (HGP符号)HGP_original Kovalevの話をしたいと思います。今回はタイトルからしてなんのこっちゃとなっている方もいらっしゃるかと思いますが、量子エラー訂正符号の話となります。
　量子エラー訂正符号として、特に表面符号が今のメジャーとなっていますが、これは論理ビットに対して必要な物理ビットの数が比較的多く、量子ビットの数を増やすのがネックとなっている現状の量子コンピューターにとってはあまり嬉しくありません。現在盛んに研究されている超伝導量子コンピューターでは、量子ビットを移動させるのが難しいため、近傍での操作だけで済んでしまう表面符号が注目されてきましたが、近年はイオントラップ型や冷却原子型のような、直接量子ビットを動かせる量子コンピューターが発展してきており、近傍の操作だけで閉じる必要がなくなってきつつあります。そこで表面符号よりも符号化率が高く、必要なビット数が比較的少ないとして注目されている符号の一つに、HGP符号があります。
　今回は一応前回の記事の続きとして、基本的な古典・量子のエラー訂正符号の知識は既知のものとしたいと思います。まだ読まれていない方は、ぜひ前回の記事を先にご覧ください。はじめに、少しだけ前回の復習として、CSS符号の鎖複体とホモロジーによる記述を見ます。次に、HGP codeの定義に必要となる、複体のテンソル積（product complex、今回は積複体と訳すことにします）の導入をします。最後にHGP符号について議論したいと思います。
　この記事の筆者はエラー訂正符号の勉強を始めたての初心者なため、ところどころ間違いが含まれている可能性がある点にはご了承ください。また、間違いを見つけた際には、コメントの方に書いていただけると大変ありがたいです。

1. CSS符号の復習

CSS符号

　$Q_2\cong\ff_2^k,\ Q_1\cong\ff_2^n,\ Q_0\cong\ff_2^k$として、以下のような$\ff_2$上の鎖複体を考える。
\begin{equation} Q_2\xrightarrow{\del_2}Q_1\xrightarrow{\del_1}Q_0 \end{equation}
$H_Z=\del_2^\trans,\,H_X=\del_1$として、論理$Z,X$演算子全体の群をホモロジー群
\begin{equation} \vb*{\bar{Z}} = \ker H_X/\im H_Z^\trans,\quad \vb*{\bar{X}} = \ker H_Z/\im H_X^\trans \end{equation}
と表す。このとき$Q_2,Q_1,Q_0$はそれぞれ$Z$stabilizer群、physical qubit、$X$stabilizer群に対応し、$H_Z,H_X$の各行が$Z,X$stabilizerに対応する。また、$\vb*{\bar{Z}}や\vb*{\bar{X}}$は論理ビットに対応する。これは量子エラー訂正符号をなしており、このような符号を$[[n,k]]$のCSS符号という。

　以下では簡単のため、$H_Z,H_X$はフルランクとします。定義からわかる通り、$\ff_2$上の長さ$2$の鎖複体を一つ持ってくると、対応するCSS符号を一つ定義することができます。実際、表面符号は単体からなる鎖複体に対応していました。ただ、全てがエラー訂正符号に適しているわけではなく、実用性を高めるためには以下のような条件を課すことが多いです。

量子低密度パリティ検査符号（qLDPC符号）

　stabilizer符号の検査行列$H$が疎、正確には、$n$や$k$によらないある自然数$M$が存在して、各行と列に対して$1$となる要素数が$M$で抑えられるような符号を、量子低密度パリティ検査符号（qLDPC符号）という。

　検査行列が疎であることは、各stabilizerを構成する物理ゲート数と、各物理ビットに関わるstabilizerの数が$n,k$などによらないことです。表面符号は各stabilizerは（おおよそ）$4$つの物理ゲートからなるため、qLDPC符号となっています。qLDPCを保ちながらいかに符号化率$k/n$と符号距離$d$を大きくするかが難しい点です。例えば符号距離$d$の表面符号に関しては、$1$論理ビットあたりおおよそ$2d^2$個もの物理ビットを必要とします。この低い符号化率を改善し、かつ符号距離も大きいような符号を構成できると嬉しいです。今回扱うHGP符号は、LDPC性を持ちつつ、比較的符号化率の高い符号も含み、かつ現実的にも比較的実装しやすい符号となっています。

古典線形符号について

　ここまで特に言及していませんでしたが、古典線形符号もCSS符号と同様に、長さ1の鎖複体$C_1\xrightarrow{H}C_0$として扱うことが可能です。ここで$H$はパリティ検査行列であり、$C_1$は符号化前のビットであり、符号空間はパリティ検査行列で0となる部分集合、すなわち$\ker H$です。

2. 積複体

　まずは、積複体とその一次元への射影となる全複体を定義します。以下の記述はreview_qldpcによります。

積複体（product complex）

　$d$個の鎖複体$C_i=\{\{C_{i,x_i}\}_{x_i\in\intset},\{\del_{i,x_i}:C_{i,x_i}\to C_{i,x_i-1}\}_{x_i\in\intset}\}$をとる。この鎖複体の$d$個のテンソル積（積複体）$E=\{\{E_\vb*{x}\}_\vb*x,\{\del_{i,\vb*{x}}:E_\vb*x\to E_{\vb*x-\vb*e_i}\}_{\vb*x}\}$を
\begin{equation} E_\vb*x = \bigotimes_{i=1}^dC_{i,x_i},\quad \del_{i,\vb*x} = \del_{i,x_i} \end{equation}
と定める。（$\del_{i,\vb*x}$の定義において、$i$番目以外の要素には恒等写像$I$がかかるが、ここでは省略した）

　ここでは一般に$d$個の積として積複体を定義しましたが、これ以降では基本的に2個または3,4個の積までしか考えないため、特に2個の積の場合を扱います。3個以上の場合は一つずつ積を取っていけば良いです。長さ$n,m$の鎖複体$C,D$の積複体は、
\begin{gather} E_{p,q} = C_p\otimes D_q\\ \partial^h_{p,q} = I\otimes\partial_q:E_{p,q}\to E_{p-1,q}\\ \partial^v_{p,q} = \partial_p\otimes I:E_{p,q}\to E_{p,q-1}\\ \end{gather}
として、$E=\{\{E_{p,q},\{\partial^h_{p,q},\partial^v_{p,q}\}_{p,q}\}$となります。
積複体

全複体（total complex）

　積複体、あるいは一般にdouble complex$E=\{\{E_{p,q}\},\{\partial^h_{p,q},\partial^v_{p,q}\}\}$の全複体$\text{Tot}(E)$を、$p+q$が等しいところのみを集めて直和を取ったものとして定める。
\begin{equation} \text{Tot}(E)_n = \bigoplus_{p+q=n}E_{p,q} \end{equation}
境界作用素は以下のように定める。
\begin{equation} \delta_n\left(\bigoplus_{p+q=n} v_{p,q}\right) = \sum_{p+q=n}\left(\partial^h_{p,q}v_{p,q}\oplus\partial^v_{p,q}v_{p,q}\right) \end{equation}
ここで$v_{p,q}\in E_{p,q}$である。

　全複体のイメージは以下の図2です。対角的に和をとってある意味で一次元に射影してやることで、CSS符号で扱う対象となる一次元の鎖複体を得ることができます。
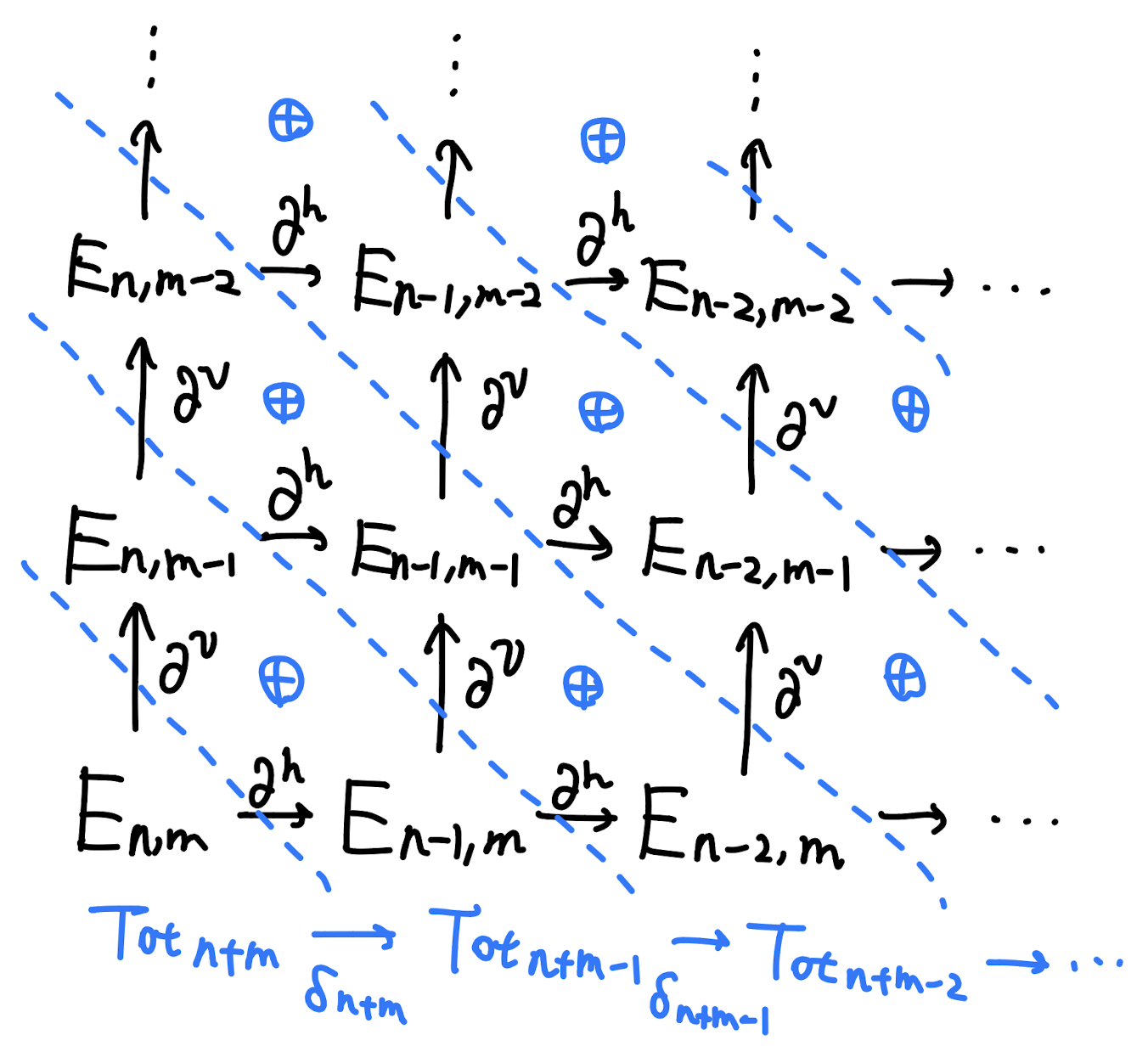全複体

3. HGP符号

　任意に取ってきた古典線形符号（特にLDPCなもの）の積として得られた鎖複体をCSS符号と見なすことで得られる新しい量子エラー訂正符号（qLDPC符号）を、Hypergraph Product code（HGP符号）と呼びます。HGP符号の特徴は、古典符号で考えられていたLDPC符号を取ってきて積を取るだけで、比較的容易にqLDPC符号を構成できる点です。
　今までは一般に長さ$n$の鎖複体と長さ$m$の鎖複体から長さ$n+m$の鎖複体を積複体の全複体として構成する方法を扱いましたが、CSS符号を構成するためには長さ2があれば十分でした。ここでは最小なものとして、長さ1の二つの鎖複体の積から長さ2の鎖複体を得ることを考えます。より長い鎖複体の上で符号を考えることは後で扱います。

HGP符号

　古典線形符号$C^1:C_0^1\xrightarrow{\partial_1^T=H_1}C_1^1$, $C^2:C_1^2\xrightarrow{\partial_2=H_2}C_0^2$をとる（それぞれ$[n_1,k_1,d_1], [n_2,k_2,d_2]$符号とする）。HGP符号$Q:Q_2\xrightarrow{\delta_2=H_Z^T}Q_1\xrightarrow{\delta_1=H_X}Q_0$を、$C^1$の転置$C_1^1\xrightarrow{\partial_1=H_1^\trans}C_0^1$と$C^2$の積複体の全複体として定める。すなわち、
\begin{gather} Q_2 = C_1^1\otimes C_1^2,\quad Q_1 = (C_0^1\otimes C_1^2)\oplus(C_1^1\otimes C_0^2),\quad Q_0 = C_0^1\otimes C_0^2\\ \end{gather}
とする。また、$v\oplus w\in Q_1$を$(v\ w)^T$のように表すことにすると、
\begin{align} \delta_2 &= \begin{pmatrix}\partial_1\otimes I_{C_1^2}\\I_{C_1^1}\otimes\partial_2\end{pmatrix} & H_Z &= \begin{pmatrix}H_1\otimes I_{n_2} & I_{n_1-k_1}\otimes H_2^T\end{pmatrix} \\ \delta_1 &= \begin{pmatrix}I_{C_0^1}\otimes\partial_2 & \partial_1\otimes I_{C_0^2}\end{pmatrix} & H_X &= \begin{pmatrix}I_{n_1}\otimes H_2 & H_1^T\otimes I_{n_2-k_2}\end{pmatrix} \end{align}
とかける。

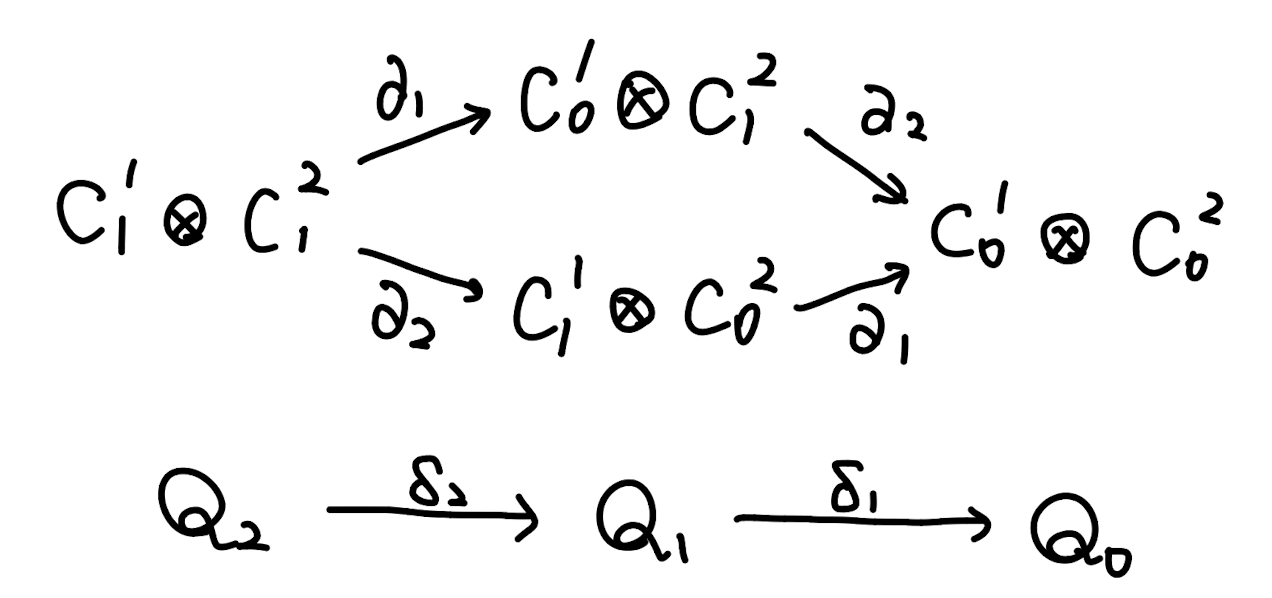HGP符号
　HGP符号は$[[n=n_1n_2+(n_1-k_1)(n_2-k_2),\,k=k_1k_2,\,d=\min(d_1,d_2)]]$符号です。
　この定義において$C^1$は$H_1$で表される古典符号の転置（パリティ行列が$H_1^T$で与えられる）となっていることに注意してください。境界作用素$\delta$の表式は以下のようにして得ることができます。$v_{1,1}\in Q_2=C_1^1\otimes C_1^2$に対して、
\begin{equation} \delta_2(v_{1,1}) = \partial_1v_{1,1}\oplus \partial_2v_{1,1} = \begin{pmatrix}\partial_1\otimes I\\I\otimes\partial_2\end{pmatrix}(v_{1,1}) \end{equation}
となります。また、$v_{0,1}\oplus v_{1,0}\in Q_1$に対して、
\begin{equation} \delta_1(v_{0,1}\oplus v_{1,0}) = \partial_2v_{0,1} + \partial_1v_{1,0} = \begin{pmatrix}I\otimes\partial_2 & \partial_1\otimes I\end{pmatrix}\begin{pmatrix}v_{0,1}\\v_{1,0}\end{pmatrix} \end{equation}
となります。
　$C^1, C^2$をそれぞれ$[n_1,k_1,d_1]$符号、$[n_2,k_2,d_2]$とすると、そこから得られるHGP符号は$[[n=n_1n_2+(n_1-k_1)(n_2-k_2),\,k=k_1k_2,\,d=\min(d_1,d_2)]]$符号となることがわかります。

HGP符号の論理$Z,X$演算子

　CSS符号の論理$Z,X$演算子は、一般に$\ker H_X/\im H_Z^T,\ \ker H_Z/\im H_X^T$で得ることができるのでした。ここでは、これを具体的に計算してみたいと思います。
　先に結果を述べると、論理$Z$演算子全体の集合$\bar{Z}$と論理$X$全体$\bar{X}$は
\begin{align} \bar{Z} &= \span\left\{\begin{pmatrix} v\otimes w \\ 0 \end{pmatrix} \middle|\,v\in (\rs H_1)^\bullet,\,w\in\ker H_2 \right\}\\ \bar{X} &= \span\left\{\begin{pmatrix} v\otimes w \\ 0 \end{pmatrix} \middle|\,v\in\ker H_1,\,w\in(\rs H_2)^\bullet \right\} \end{align}
となります。ここで、ベクトル空間$V$の部分空間$W$に対して、$W^\bullet$は$W\oplus W^\bullet=V$となる空間（補空間）です。$W^\bullet$は一意ではないため、任意に一つ固定することにします。また、$\rs H = \im H^T$は$H$の行空間（$H$の行からなるベクトル全体）です。

　ここで、$V\subseteq\mathbb{F}_2^n$のとき、直交補空間$V^\perp$は必ずしも補空間になるとは限りません。例えば、以下の$V^\perp$は $(1,1,1)^\mathrm{T}+(0,1,0)^\mathrm{T}=(1,0,1)^\mathrm{T}$から$V$の補空間ではないですが、直交補空間です。
\begin{align} V = \span\left\{ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \right\},\ V^\perp = \span\left\{ \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \right\},\ V^\bullet = \span\left\{ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right\}\,\text{etc.} \end{align}
一般に、内積空間において直交補空間は補空間となりますが、$V\in\mathbb{F}_2^n$における典型的な内積$\langle v,w\rangle = \sum_iv_iw_i\ \mathop{\text{mod}}2$は、$\langle v,v\rangle=0$と$v=0$が同値でないために内積空間とならず、一般には$(\rs H_1)^\bullet \neq (\rs H_1)^\perp = \ker H_1$です。

　$Z$と$X$で示すべきことはほとんど変わらないため、ここでは$Z$のみ詳しく見たいと思います。ここでの記述はreshape partitioningに依ります。また、少し見づらくなりますが、ここでは単位行列$I$を明示することにします。

　$v\in C_0^1\otimes C_1^2,\,w\in C_1^1\otimes C_0^2$として、$\begin{pmatrix}v\\w\end{pmatrix} \in Q_1$を任意に取ります。$\ker\delta_1$の任意の要素は$(I\otimes\partial_2)v + (\partial_1\otimes I)w = 0$、すなわち$(I\otimes\partial_2)v = (\partial_1\otimes I)w \eqqcolon u$を満たします。ここで、$u\in\im(I\otimes\partial_2)\cap\im(\partial_1\otimes I)=\im(\partial_1\otimes\partial_2) = (I\otimes\partial_2)(\partial_1\otimes I)Q_0$です。$(I\otimes\partial_2)v + u = (\partial_1\otimes I)w + u = 0$から$(I\otimes\partial_2)v=(\partial_1\otimes I)w=u$であるので、
\begin{align} v&\in\im(\partial_1\otimes I) + \ker(I\otimes\partial_2) = \im\partial_1\otimes C_1^2 + C_0^1\otimes\ker\partial_2\\ w&\in\im(I\otimes\partial_2) + \ker(\partial_1\otimes I) = C_1^1\otimes\im\partial_2 + \ker\partial_1\otimes C_0^2 \end{align}
が成り立ちます。また、上の集合の任意の要素$v,w$は$\delta_1 \begin{pmatrix}v\\w\end{pmatrix}=0$を満たします。よって、$\ker\delta_1$は
\begin{align} &\ker\delta_1\\ &= \left\{\begin{pmatrix} v \\ w \end{pmatrix} \middle|\, v\in\im\partial_1\otimes C_1^2 + C_0^1\otimes\ker\partial_2,\ w\in C_1^1\otimes\im\partial_2 + \ker\partial_1\otimes C_0^2 \right\}\\ &= \im\delta_2 + \left\{\begin{pmatrix} v \\ w \end{pmatrix} \middle|\,v\in C_0^1\otimes\ker\partial_2,\ w\in\ker\partial_1\otimes C_0^2 \right\} \end{align}
となります。論理$Z$演算子は商集合$\ker\delta_1/\im\delta_2$で与えられます。
　上の式の第2項は第1項との共通部分を持つため、それを除き、$\im\delta_2$との直和の形になるように変形します。$v$を$v=v_1\otimes v_2$すなわち$v_1\in C_0^1$、$v_2\in\ker\partial_2$、と分解できるとして、$v_0 + v^\bullet=v_1$ $(v_0\in\im\partial_1, v^\bullet\in(\im\partial_1)^\bullet)$なるものをとリます。同様に$w$に対して、$w_1,\,w_2,\,w_0,\,w^\bullet$を取ります。このとき$\begin{pmatrix} v \\ w \end{pmatrix}$は直和の形に分解することができて、$\begin{pmatrix} (v_0\oplus v^\bullet)\otimes v_2\\ (w_0\oplus w^\bullet)\otimes w_2 \end{pmatrix} = \begin{pmatrix} v_0\otimes v_2\\ w_0\otimes w_2 \end{pmatrix} \oplus \begin{pmatrix} v^\bullet\otimes v_2\\ w^\bullet\otimes w_2 \end{pmatrix}$となり、$\begin{pmatrix} v_0\otimes v_2\\ w_0\otimes w_2 \end{pmatrix}$は$\im\delta_2$に含まれます。もし$v$と$w$が直積の形に書けなかったとしても、$v=\sum_{i,j}c_{i,j}v'_i\otimes v''_j,\,w=\sum{i,j}d{i,j}w'_i\otimes w''_j$のように分解して同様に考えることで同じ結論が得られます。よって、論理$Z$演算子は
\begin{align} \bar{Z} &= \ker\delta_1/\im\delta_2\\ &= \left\{ \begin{pmatrix} v \\ w \end{pmatrix} \middle|\,v\in (\im\partial_1^1)^\bullet\otimes\ker\partial_2,\ w\in\ker \partial_1\otimes (\im\partial_1^2)^\bullet \right\}\\ &= \left\{ \begin{pmatrix} v \\ w \end{pmatrix} \middle|\,v\in (\rs H_1)^\bullet\otimes\ker H_2,\ w\in\ker H_1^T\otimes (\rs H_2^T)^\bullet \right\} \end{align}
のように得ることができました。$H_1$と$H_2$はフルランクなので$\ker H_1^T=0$, $\rs H_2^T = C_0^2$であることから、
\begin{equation} \bar{Z} = \span\left\{ \begin{pmatrix} v\otimes w \\ 0 \end{pmatrix} \middle|\,v\in (\rs H_1)^\bullet,\,w\in\ker H_2 \right\} \end{equation}
となります。

例

　ここでHGP符号の例として、$[7,4,3]$Hamming符号の積を考えます。パリティ検査行列と生成行列は
\begin{equation} H = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{pmatrix},\quad G = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1 & 1 & 1 & 1\\ \end{pmatrix} \end{equation}
で与えられます。$H_1=H_2=H$としてHGP符号を構成すると、$[[58,16,3]]$符号を得ることができます。これは、例えば$[[2d^2-1,1,d]]$表面符号の$d=3$よりも高い符号化率を達成しています。一方で、Hamming符号を直感的に拡張した以下のような符号では、$k$が奇数のときはHGP符号を構成できるものの、LDPC性を満たしません。
\begin{equation} H = \left( \begin{array}{cccc|c|cccc} 0 & 1 & \cdots & 1 & 1 & 1 & 0 & \cdots & 0\\ 1 & 0 & \cdots & 1 & 1 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & 1 & \cdots & 0 & 1 & 0 & 0 & \cdots & 1\\ \end{array} \right) \end{equation}
　$[7,4,3]$Hamming符号から作られるHGP符号の論理演算子は、行空間$\rs H$の補空間として$e_i\ (i=1,2,3,4)$で貼られる空間を考えて（ここで$e_1=(1,0,0,0,0,0,0)^T$など）、$G$の4つの列のベクトルを$g_1,g_2,g_3,g_4$で表すことにすると、
\begin{align} \bar{Z} &= \span\{e_i\otimes g_j\mid i,j=1,2,3,4\}\\ \bar{X} &= \span\{g_j\otimes e_i\mid i,j=1,2,3,4\} \end{align}
と表すことができます。このとき$e_i^Tg_j = \delta_{i,j}$が成り立っているので、各$(i,j)$に対して、$(e_i\otimes g_j)^T(g_{j'}\otimes e_{i'}) = \delta_{i,i'}\delta_{j,j'}$です。すなわち$e_i\otimes g_j$と$g_j\otimes e_i$で一つの論理量子ビットを表すことがわかります。
　また2025年の研究chgpでは、古典符号$C^1,C^2$の両方またはいずれかを巡回符号にすると、比較的符号化率の良い符号、例えば$[[1922,200,12]]$符号が得られています。

少しまとめ

　色々と書きましたが、HGP符号とは検査行列を
\begin{align} H_X &= \begin{pmatrix}I\otimes H_2 & H_1^T\otimes I\end{pmatrix}\\ H_Z &= \begin{pmatrix}H_1\otimes I & I\otimes H_2^T\end{pmatrix} \end{align}
で定めた符号です。$n_1=n_2$, $k_1=k_2$, $d_1=d_2$とすると、HGP符号は$[[2n^2-2nk+k^2,\ k^2,\ d]]$符号です。古典符号の効率が良ければ、対応するHGP符号も比較的良い符号となることがわかります

3. 表面符号のHGP符号としての表現

　最後におまけとして、HGP符号が通常の2次元の表面符号や、より高次元の表面符号を内包していることをみたいと思いますexp_4d_surface。
　パリティ検査行列を
\begin{equation} H = \left( \begin{array}{} 1 & 1 & 0 & \cdots & 0\\ 0 & 1 & 1 & \ddots & \vdots\\ \vdots & \ddots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & 1 & 1 \end{array} \right) \end{equation}
とした古典$[L,1,L]$反復符号$C$に対して、$C$と$C^T$の積から作るHGP符号は$[[2L^2-1,1,L]]$表面符号になります。以下では、実際に2次元の表面符号が得られるか計算してみたいと思います。
　一般の大きな符号では少し大変なので、$L=3$の場合で考えてみます。このとき
\begin{equation} H = \left( \begin{array}{} 1 & 1 & 0\\ 0 & 1 & 1 \end{array} \right) \end{equation}
です。$H_Z$,$H_X$は以下のように計算できます。
\begin{align} H_Z &= \left(\begin{array}{c|c}H\otimes I_3 & I_2\otimes H^T\end{array}\right) = \left( \begin{array}{ccccccccc|cccc} 1&&&1&&&&&&1&&&\\ &1&&&1&&&&&1&1&&\\ &&1&&&1&&&&&1&&\\ &&&1&&&1&&&&&1&\\ &&&&1&&&1&&&&1&1\\ &&&&&1&&&1&&&&1 \end{array} \right)\\ H_X &= \left(\begin{array}{c|c}I_3\otimes H & H^T\otimes I_2\end{array}\right) = \left( \begin{array}{ccccccccc|cccc} 1&1&&&&&&&&1&&&\\ &1&1&&&&&&&&1&&\\ &&&1&1&&&&&1&&1&\\ &&&&1&1&&&&&1&&1\\ &&&&&&1&1&&&&1&\\ &&&&&&&1&1&&&&1\\ \end{array} \right)\\ \end{align}
すでに行列が巨大すぎてしんどいですが、これを図示すると、以下のように見慣れた表面符号が現れます。ここで、赤色で書いたものは$Z$stabilizer、青色で描いたものが$X$stabilizerで、頂点が物理ビットに対応しています。また、上の行列で順番に番号を振った際のそれぞれのstabilizer、qubitの番号も示してあります。
!FORMULA[188][36286094][0]の表面符号 $d=3$の表面符号
　また、$\ker H=\{(1,1,1)^T\}$、$(\rs H)^\bullet$は$\{(1,0,0)^T\},\{(0,1,0)^T\},\{(0,0,1)^T\}$のいずれかです。これより論理$Z$演算子を考えると、例えば$(1,1,1)^T\otimes(1,0,0)^T$となります。これは$1,4,7$番目のqubitに作用していて、通常の表面符号と同じものになることがわかります。また、他の$(\rs H)^\bullet$を考えると$X_2X_5X_8$, $X_3X_6X_9$となり、$(\rs H)^\bullet$の任意性はどの縦方向の列を選ぶかに対応していることがわかります。

　このようにして得られた2次元表面符号に、さらに古典$[L,1,L]$符号$C$（またはその転置）をかけていくことで、より高次元の表面符号を得ることができます。構造は2次元までとほとんど同じで、例えば、立方体、その表面、その辺が$Z$stabilizer、qubit、$X$stabilizerのようになります。$C$を一つかけるごとに、その全複体の長さは1ずつ増えていきます。そのうち、任意の長さが2の部分を量子エラー訂正符号と見ることができます。3次元以上では少し余る部分がありますが、これは測定結果の古典チェック（メタチェック）として使うことができます。例えば、以下のような鎖複体が得られたとして、$Q_3,Q_2,Q_1$を量子エラー訂正に使うとします。このとき、$Q_3\xrightarrow{\partial_4^T}Q_4$と$Q_1\xrightarrow{\partial_1}Q_0$は、それぞれ$Z$測定、$X$測定結果という古典情報に対する古典エラー訂正符号と見ることができ、古典的にもエラーを検知、訂正できることになります。具体的に検査行列などを書き下したものについてはexp_4d_surfaceをご参照ください。

4. おわりに

　今回はqLDPC符号の中でも、HGP符号について扱いました。個人的にはあまりウケにくい記事になってしまった印象があるのですが、楽しんでいただけたでしょうか。量子エラー訂正の世界は最近特に発展が早く、新しい符号が次々に考えられていますが、その中でもHGP符号は、比較的符号化率がよく、自由度が高いため、長く生き残ってくれると嬉しいですね。