経済学とゲージ理論 −"価値空間"の幾何学−
※ 本記事は Mathlog Advent Calendar 2023 大学数学部門にエントリーしています。
※ noteに
関連記事
がありますが同一筆者です。
はじめに
今の世の中様々な事物に関して貨幣による価格が付与されており、それは事物の相対価値の指標としての役割を果たします。そしてその価値は政府や企業や個々人の経済活動によりダイナミカルに変化します。そのダイナミクスを理論化し分析することは、金融工学やファイナンス理論、ひいては経済学のひとつの目標かと思います。
ところで、あらゆる事物の価値の数値化がなされているなら、それを幾何学的に理解することもできるのではないでしょうか。そしてそれは実際に可能です。本記事では為替取引や一般的な資産取引における「裁定取引(arbitrage)」をリーマン幾何学における曲率とみなし、そこに潜むゲージ理論的な構造に関して述べます。
いくつかコメントです。
- 参考文献に関して。本記事は主にSchwichtenbergIlinski-01に基づきます。Ilinski-01Ilinski-02Farinelli-01Farinelli-02Farinelli-03は原著論文です。Rodriguesはファイナンスにおけるゲージ理論的アプローチを総合的にまとめた博士論文です。Yamamotoは計算ファイナンスの基礎に関する講義録です。
- 本記事ではゲージ理論という言葉を使いますが、数学的にはファイバーバンドルと言った方が良いかもしれません。参考文献ではきちんとファイバーバンドルの構成を行っています。
- 経済学上の概念に関しては不正確な部分もあるかもしれないのでご注意ください。
為替裁定取引のゲージ理論
デノミネーション
デノミネーション(以下デノミと呼ぶ)とは「通貨の呼称単位の切り下げまたは変更」のことです。例えばある日の1000円を、明日から10000円とか100円にするような行為です。デノミは各国通貨で独立に行えます。
デノミを定量化しておきます:
\begin{align}
\text{「通貨を}\alpha\text{倍にデノミする」} = \text{「デノミ前の通貨1単位の価値と、デノミ後の通貨}\alpha\text{の価値を等しくする」}
\end{align}
デノミ前にある物の価格が通貨1単位であった場合デノミ後の通貨では$\alpha$になるので、$\alpha$倍のデノミで通貨の価値は$1/\alpha$になります。
為替相場に対するデノミの影響を考えます。為替相場$R_{ij}$を以下のように定義します:
\begin{align} R_{ij} = 「i\text{国の通貨1単位の価値を}j\text{国の通貨で表した値}」 \end{align}
$i,j$は国のラベルです。$i$国が$\alpha$倍の通貨のデノミを行えば為替相場は$R_{ij}\to R_{ij}/\alpha$のように変化します。例えば$\alpha=2$なら$i$国の通貨の価値は半分になるため、それを$j$国の通貨で表した価格も半分になります。$i$国が$\alpha$倍、$j$国が$\beta$倍のデノミを行えば
\begin{align}
R_{ij}\to R_{ij}\times \beta/\alpha \tag{1}\label{eq1}
\end{align}
と変化します。$i,j$のインデックスの順番は重要です。次の関係式が成立します:$R_{ji}=1/R_{ij}$。
デノミは各国の通貨の価値を表現するための局所座標のスケールに関する変換と言えます。
裁定取引の指標
各国がデノミを行えば為替相場は変動しますが、これは経済活動を通じて起こる「価値のダイナミクス」とは無関係な、単なる表現上の変動です。ではどうしたら「各国のデノミに依存しない重要な情報」を表す量を得られるでしょうか?ここでは為替における裁定取引を為替相場の重要な情報であると定義し考察の対象とします。為替取引における裁定取引とは
ある通貨Aで現金を所有しているとき、ある特定の時刻の為替相場によりこれを通貨B,C,D,...に次々に換金し、最後に通貨Aに戻したときに最初の金額より増える/減ること
です。つまりある時刻においてループ状の換金を行った時元手が増減することです。このようなことが起こるのは、各国の通貨の価値付けが「じゃんけんの強さの順」のようにループした後に戻らず歪んでいることに由来します。
次に裁定取引でどれだけ儲かる/損するかを示す指標を作ります。ここでは4国間の裁定取引を考えます。図1よりそれは
\begin{align} M_{ijkl}=R_{ij}R_{jk}R_{kl}R_{li}\\ {} \end{align}
 4国間取引による利益率
4国間取引による利益率
であることがわかります。$M_{ijkl}\neq 1$のとき裁定取引です。$i$国の通貨の元手を$x$としてこの取引を行うと、最終的に得られる金額は$xM_{ijkl}$です。
そしてこの量は各国のデノミで不変です。実際$i,j,k,l$の各国がそれぞれ$\alpha,\beta,\gamma,\delta$とすると
\begin{align}
M_{ijkl}\to \beta R_{ij}/\alpha\times \gamma R_{jk}/\beta\times \delta R_{kl}/\gamma\times \alpha R_{li}/\delta=M_{ijkl}
\end{align}
となります。こうして$M_{ijkl}$は
- (4国間)裁定取引の指標である
- 各国のデノミに対して不変
という望ましい性質を備えていることがわかります。
格子上の世界と為替相場
各国を格子上に配置することでこれらの量をゲージ場の理論と対応させます。以下のように世界を設定します:
- 世界は$d$次元。格子点を$n=(n_1,n_2,\ldots,n_d)$で表す
- 格子点上に国が存在する
- 隣接国の間の為替相場を$R_\mu(n)$で表す。これは「格子点$n$に存在する国と格子点$n+\hat\mu$($\hat\mu$: $\mu$方向の単位ベクトル。$\mu$方向の隣)に存在する国の間の為替相場」のこと
- 格子上の隣接した4国間における$M_{ijkl}$を
\begin{align} M_{\mu\nu}(n):=R_\mu(n) R_\nu(n+\hat\mu) /R_\mu(n+\hat\nu) /R_\nu(n) \end{align}
で定義する
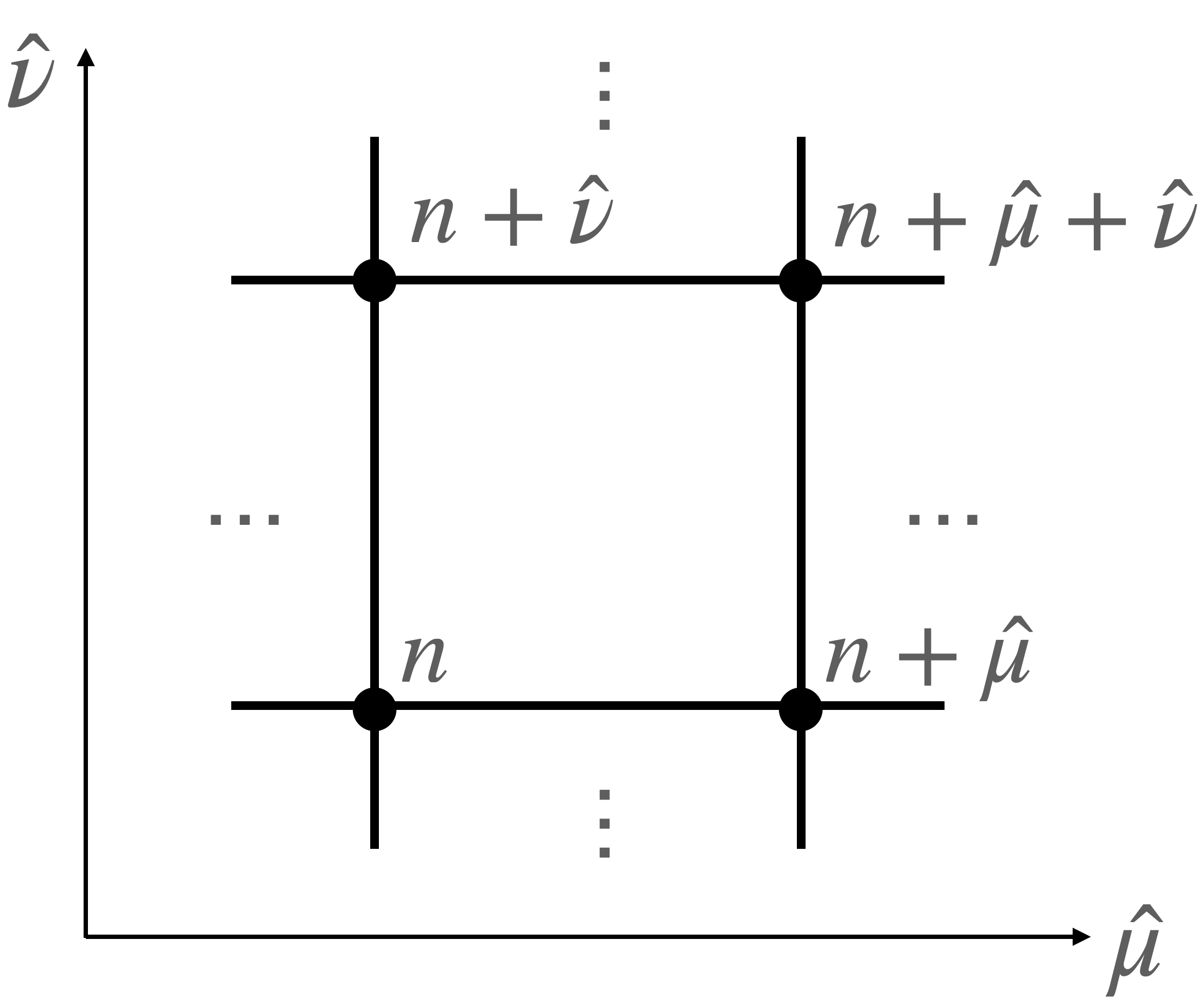 格子上の国々とその座標付け
格子上の国々とその座標付け
ここで$d$は時刻まで含んでいるとします。$d=4$なら「空間3次元+時間1次元」です。よって$\mu$は時間方向もとります(例えば$\mu=d$が時間方向とする)。$\mu$が時間方向の場合$R_\mu(n)$は「違う時刻の同通貨の間の為替相場」なので、このとき$M_{\mu\nu}$は裁定取引とはちょっと違うのですが、概念を拡張します。または違う時刻の国を違う国とみなしていると考えればよいかと思います。
各国がデノミネーションを行ったとして、その倍率を$g(n)$とします。このとき$R_\mu(n)$は
\begin{align}
R_\mu(n)\to g^{-1}(n)R_\mu(n)g(n+\hat\mu)
\end{align}
と変化することはEq.\eqref{eq1}から明らかかと思います。また$M_{\mu\nu}(n)$がこの変換に対して不変であることも簡単にわかります:
\begin{align}
M_{\mu\nu}(n)&\to \frac{g^{-1}(n)R_\mu(n)g(n+\hat\mu)g^{-1}(n+\hat\mu)R_\nu(n+\hat\mu)g(n+\hat\mu+\hat\nu)}{g^{-1}(n+\hat\nu)R_\mu(n+\hat\nu)g(n+\hat\nu+\hat\mu)g^{-1}(n)R_\nu(n)g(n+\hat\nu)}
=M_{\mu\nu}(n)
\end{align}
裁定取引とゲージ理論との対応
連続極限
ここで国家間の為替相場に連続性(や微分可能性)を取り入れます。すなわち十分に近い国家間の為替相場は十分に1に近いとします。
距離の概念を取り入れるために格子点の間隔を$a$とします。また$x:=an$と定義します。世界の一方向の格子点の数を$N$とし、$L:=aN$を固定して$a\to 0, N\to \infty$の極限をとることで$x$を連続化します。これを連続極限と呼ぶことにします。
今まで$A_\mu(n)$と書いていたものを$\hat A_\mu(n)$と表記することにして、$aA_\mu(x):=\hat A_\mu(n)$とします。このとき
\begin{align}
R_\mu(n)&=\exp(a A_\mu(x))\xrightarrow{\text{連続極限・テイラー展開}} 1+aA_\mu(x),\\
M_{\mu\nu}(n)&=\exp\left[a\left\{A_\mu(x)+A_\nu(x+a\hat\mu)-A_\mu(x+a\hat\nu)-A_\nu(x)\right\}\right]\\
&\xrightarrow{\text{連続極限・テイラー展開}}\exp\left[a^2\left\{\partial_\mu A_\nu(x)-\partial_\nu A_\mu(x)\right\}\right]
=:\exp(a^2F_{\mu\nu}(x))\\
&F_{\mu\nu}(x):=\partial_\mu A_\nu(x)-\partial_\nu A_\mu(x)
\end{align}
同様に$g$もexponentiateして$g(n)=\exp(\theta(n))$とすればデノミは
\begin{align}
R_\mu(n)=\exp(aA_\mu(x)) &\xrightarrow{\text{デノミ}} \exp(aA_\mu(x)+(\theta(x+a\hat\mu)-\theta(x)))
\end{align}
になります。デノミの左辺と右辺で連続極限をとれば
\begin{align}
A_\mu(x)\xrightarrow{\text{デノミ}} A_\mu(x)+\partial_\mu \theta(x)
\end{align}
となります。
ゲージ理論との対応: 連続極限
ここまでくれば、Maxwell方程式をゲージ場で表す形式に馴染みある方には対応関係がわかると思います。 この記事 を見るとわかるように、$A_\mu(x)$はゲージ場、$F_{\mu\nu}(x)$は場の強さ(時間-空間成分は電場、空間-空間成分は磁場に対応する)、デノミはゲージ変換、$\theta(x)$はゲージ変換の関数に対応しています。対応を表にまとめれば以下のようになります:
\begin{array}{ccc}
\hline
\text{連続極限の為替相場}& &\text{連続理論におけるゲージ理論}\\
\hline
\text{隣国間の為替相場} R_\mu(n)\text{の対数}&\leftrightarrow& \text{ゲージ場}A_\mu\\
M_{\mu\nu}(n) \text{の対数}&\leftrightarrow& \text{場の強さ}F_{\mu\nu}\\
\text{デノミネーションの対数}&\leftrightarrow & \text{ゲージ変換}\\
\text{デノミネーションの倍率}g(n)\text{の対数}&\leftrightarrow & \text{ゲージ変換関数}\\
\hline
\end{array}
ゲージ場はリーマン幾何学の言葉で言えば接続に当たります。そして場の強さ$F_{\mu\nu}$は曲率です。すなわち
${}$
${}$
と言えます。
ただし為替相場とゲージ理論にはひとつ大きな違いがあります。電磁気学のゲージ群(数学で言えばファイバーに作用する構造群)はU(1)なので位相変換ですが、裁定取引では${\mathbb R}_+$の元によるスケール変換です。
ゲージ理論との対応: 格子ゲージ理論
以上見たように、為替相場に現れる各量の対数がゲージ理論の変数に対応しています。これは連続極限のゲージ場の理論では変換群に付随するLie代数の元を場として扱うことに由来します。一方格子上のゲージ理論では、為替相場の各量は格子ゲージ理論の各量に直接対応します。これは格子上ではLie群の元を基本的な変数として扱うことに由来します。$R_\mu(n)$は格子ゲージ理論ではリンク変数、$M_{\mu\nu}$はプラケットと呼ばれます。デノミは格子上のゲージ変換:$R_\mu(n)\to g^{-1}(n)R_{\mu}(n)g(n+\hat\mu)$です。まとめると以下の表のようになります:
\begin{array}{ccc}
\hline
\text{為替相場}& &\text{格子上のゲージ理論}\\
\hline
\text{隣国間の為替相場} R_\mu(n) &\leftrightarrow& \text{リンク変数}\\
M_{\mu\nu}(n)&\leftrightarrow& \text{プラケット}\\
\text{デノミネーション}&\leftrightarrow & \text{格子上のゲージ変換}\\
\text{デノミネーションの倍率}g(n)&\leftrightarrow & \text{格子上のゲージ変換の因子}\\
\hline
\end{array}
${}$
![リンク変数 !FORMULA[80][672215892][0](左図)とプラケット!FORMULA[81][-289638118][0](右図)](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F7k3r2kWrKPbAuaZvPD1q.png?alt=media) リンク変数 $R_\mu(n)$(左図)とプラケット$M_{\mu\nu}(n)$(右図)
リンク変数 $R_\mu(n)$(左図)とプラケット$M_{\mu\nu}(n)$(右図)
${}$
 格子上のゲージ変換
格子上のゲージ変換
時空を離散化すると$A$や$F$で記述された理論ではゲージ対称性が破れます。またこれらの量はその値に上限・下限がなく、数値計算では扱いにくいです。一方格子上のゲージ理論では上記のゲージ対称性が厳密に保たれ、また各変数も有界な値を持ちます。
ただし為替取引の場合対称性がスケール変換なので、$R,M$は有界ではなくなります。
ちなみにプラケットは隣接した4点を結ぶリンク変数のループですが、隣接点以外のループも含めた概念をWilsonループ(数学的にはホロノミーに相当する)、リンク変数の積でループになっていない開いたラインはWilsonラインなどと呼ばれます。
物質場 = 物や通貨
ゲージ場と為替相場の対応はわかりました。では電子などの物質場に対応する為替の概念はなんでしょうか。答えは現金です。裁定取引が起こると儲かる方向のループに取引が行われ、現金がその方向に流れます。これは現金が電荷を持っており、裁定取引の方向に電場が生じたために電荷に力が働きそちらに流れたと解釈できます。ところが現金が流れると、買われた通貨は高く売られた通貨は安くなります。これは裁定取引を解消する効果として働きます。現金の流れの保存則はカレントの保存則に対応します。市場の安定性のためには現金の流れを考慮することが重要です。
保存カレントに関してもゲージ場と同様対応関係を具体的に構成できますが、本記事では割愛します。
資産取引におけるゲージ理論
以上は為替取引の話でしたが、以下一般的な資産取引に話を移します。
資産取引
企業や個人は資産を運用して増やします。そのための商品として株、為替、債権、年金・保険等様々なものがあります。取引で大損害を被るリスクを避けるための金融派生証券(デリバティブ)というものもあります。今や資産運用は常識とも言える時代です。現代の激しい国際競争社会において、特に大組織は(哀しいかな)資金の大きさが勝負を分けます。
記事執筆時点において、野球の大谷選手の契約が「10年で1050億円。ただし殆ど後払い」ということで話題ですが、今の1000億円と10年後の1000億円では価値が違います。運用して利益が出るか否かはもちろん商品や場合によりますが、例えば銀行預金や国債などの債券は事前に利率がわかっており、安全な資産運用かつ基準となる運用法です。このような資産運用により10年で$e^{r}$倍に資産が増えるなら、10年後の1000億円は今の(1000億円$\times e^{-r}$)の価値ということになります。今と将来で額面上同額なら、今の額の方が価値が高いです。現金に限らず全ての資産はそのような性質を持ちます。経済学ではこのような考えをするのが普通であり、$e^{-r}$のような未来の資産を現在の資産に換算する比率をdiscount rateと呼びます。
一般的な資産取引における裁定取引
いま2つの資産があるとします。ひとつは現金であり、これを銀行に預け、その利息で利益を得ることにします。もうひとつは何でもいいですが株にします。各時刻を$T_i$のように表し、図5のような状況を考えます。
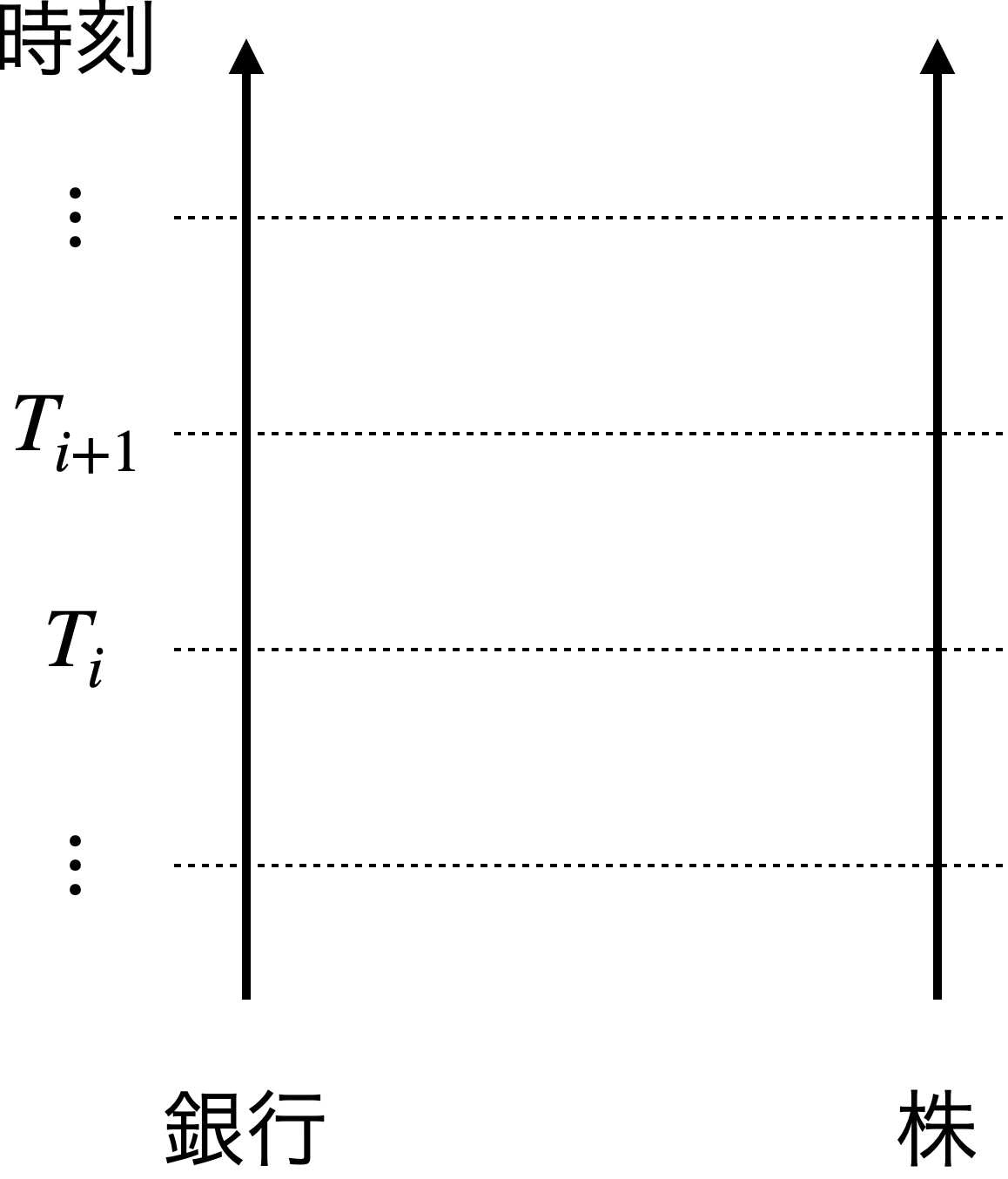 2資産取引の世界
2資産取引の世界
ある時刻$T_i$における株1単位の値段を$S_i$とします。銀行に預けたお金は、時間が$\Delta$だけ経過すると$e^{r_1\Delta}$倍になることにします。一方株は同じ時間間隔で$e^{r_2\Delta}$倍になるとします。
 銀行預金と株の取引ルートとそのレート
銀行預金と株の取引ルートとそのレート
この2つの資産を用い、2つの違う取引の仕方を考えます。
- ある時刻$T_i$で現金を1単位銀行に預け、$\Delta$だけ時間経過した$T_{i+1}$で現金を引き出し、株をそのお金で買える分買う
- $T_i$で現金1単位分の株を買い$T_{i+1}$まで所有する
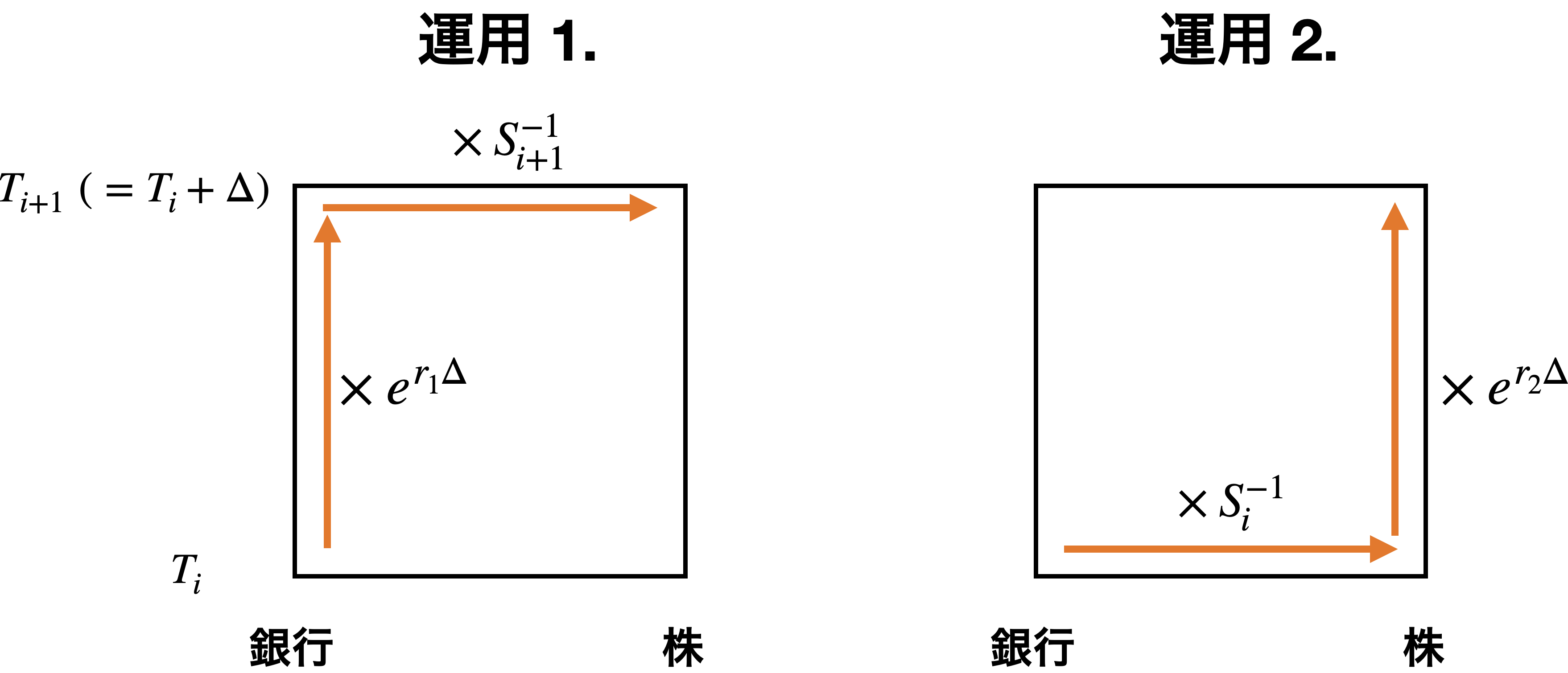 取引1.と2.の概念図
取引1.と2.の概念図
取引1.の場合、時刻$T_{i+1}$で$e^{r_1\Delta}S_{i+1}^{-1}$だけ株を所有しています。一方2.の場合$S_i^{-1}e^{r_2\Delta}$だけ所有しています。$e^{r_1\Delta}S_{i+1}^{-1}>S_i^{-1}e^{r_2\Delta}$なら1.がお得、$e^{r_1\Delta}S_{i+1}^{-1}< S_i^{-1}e^{r_2\Delta}$なら2.がお得です。
この2つの取引は始点と終点が同じです。すなわち時刻とどの資産を保有しているかは1.と2.の始めと終わりで同じです。しかしながら最終的に得られる株は一般には異なります。2つの経路による株の比率(「1.による株」/「2.による株」)は
\begin{align}
e^{r_1\Delta}S_{i+1}^{-1}/(S_i^{-1}e^{r_2\Delta})
\end{align}
であり、これから1を引いた値が1.と2.の「歪み」を表します。よって単位時間あたりの歪みを表す指標は、1.2.の取引を平均して
\begin{align}
&\left[e^{r_1\Delta}S_{i+1}^{-1}/(S_i^{-1}e^{r_2\Delta})-1
+\left\{e^{r_1\Delta}S_{i+1}^{-1}/(S_i^{-1}e^{r_2\Delta})\right\}^{-1}-1\right]/2\Delta\\
&=\left[S_i^{-1}e^{r_2\Delta}S_{i+1}e^{-r_1\Delta}+S_ie^{r_1\Delta}S_{i+1}^{-1}e^{-r_2\Delta}-2\right]/2\Delta\\
&=:s_{gauge} \tag{1} \label{Eq1}
\end{align}
となります。$e^{r_1\Delta},e^{r_2\Delta}$をゲージ理論における時間方向のリンク変数、$S_i,S_{i+1}$を空間方向のリンク変数と思えば、これは「右回りプラケットと左回りプラケットから2を引いた値の平均」です。
この場合のゲージ対称性は各資産の各時刻における単位の変更に当たります。為替取引におけるデノミと同様であり、この変更で上の式が不変なのは簡単に確かめられますし、直感的にもほぼ明らかかと思います。
一方格子ゲージ理論におけるゲージ場の作用$S^{\rm lat}$の最もシンプルなものは以下のように書けます:
\begin{align}
S^{\rm lat}=\beta\sum_{n,\mu\neq \nu}{\rm tr}[U_\mu(n)U_\nu(n+\hat\mu)U^{-1}_{\mu}(n+\hat\nu)U^{-1}_\nu(n)] \tag{2}\label{Eq2}
\end{align}
ここではリンク変数を$U_\mu(n)$で表しています。これは$\mu\neq\nu$で足し上げていることから、右回りと左回りのプラケットを足したものであり、定数項を除きEq.\eqref{Eq1}と同じ形をしています。${\rm tr}$がついているのはゲージ群が非可換の場合も含むようにするためです。
経路積分量子化と幾何ブラウン運動
このようなゲージ理論的な視点において、為替相場のダイナミクスはどのように記述されるでしょうか。Ilinski-01では以下のような原理を置くことで資産の価格変動のダイナミクスを記述する作用および確率分布を導いています:
【公理1】 ゲージ不変なダイナミクス
$\hspace 1.8cm$ すべての取引状況は資産の単位の選択に依存しない
【公理2】 局所性
$\hspace 1.8cm$ 資産はそれと取引可能な資産とのみ影響し合う
【公理3】 自由場の理論 - 対応原理
$\hspace 1.8cm$ 作用はプラケットに関して線形である
$\hspace 1.8cm$ → 物質場がない時には自由場の作用に等しく、為替や利益率に関してブラウン運動を導く。
【公理4】 作用の極値原理
$\hspace 1.8cm$ どんな資産取引に対しても、その環境下で可能な「最小の利益」しか得られない。
$\hspace 1.8cm$ ここで利益の大きさの基準は安全な資産運用(銀行預金、債権等)による利益である。
$\hspace 1.8cm$ (投資家が完全に合理的な場合は安全資産の運用利益を上回る運用法はありえない)
【公理5】 有限の合理性と不確定性
$\hspace 1.8cm$ 投資家の合理性は有限であり、時に裁定取引のような「不合理な利益」が存在する。
$\hspace 1.8cm$ そのような利益は作用により定まる分布により確率的に起こる。
これらの公理より、前章の$S$(株価)の従う確率分布$P(\{S\})$を構築します。前章Eq.\eqref{Eq1}の$s_{\rm gauge}$は【公理1,2】を満たします。【公理5】より確率的な変動の要素を加えます。その確率は裁定取引$s_{\rm gauge}$が大きければその確率は低く、逆に小さければその確率が高いのが自然です。また「温度」に相当するパラメータを取り入れ、これが小さければ系の揺らぎは小さく作用を最小化する状況が実現するようにします。これらを満たすために、系は"ハミルトニアン"(=時間をEucllid化して空間化した場合の作用)$s_{\rm gauge}$による温度$1/\beta$のカノニカル分布に従うとします:
\begin{align} P(\{S\})\sim e^{-\beta s_{gauge}(S)} \end{align}
ここで系にゲージ固定を課します。ここではゲージ理論におけるaxial gauge =「時間方向のゲージ場の固定」に対応するゲージ固定を採用します。このとき時間方向のリンク変数に対応する$e^{r_1},e^{r_2}$は固定され、$r_1,r_2$は定数になります。こうしてダイナミカルな変数は株価$S_i$のみになります。
$P(\{S\})$を$S$に関して"汎関数積分"すれば、系の分配関数を得ます。このとき重要なのは、分配関数がゲージ不変性を保つように、汎関数積分の測度をHaar measure(ゲージ変換に対して不変な測度)にすることです。$S_i$のスケール変換(=資産を測る単位の変更)に対応するHaar measureは$dS_i/S_i$です。これが$S_i$のスケール変換に対して不変なのは明らかかと思います。ここで$t=T_0=0$と$t=T_N=T$での$S$の値を固定し、それぞれ$S(0)=S_0, S(T)=S$とします。このとき$S(0)=S_0, S(T)=S$となる分布関数は以下のようになります:
\begin{align}
P(t=0,S_0;t=T,S)=\int_0^\infty\cdots\int_0^\infty
\prod_{i=1}^{N-1}\frac{dS_i}{S_i}
\exp\left[
-\frac{\beta}{2\Delta}\sum_{i=1}^{N-1}(S_i^{-1}e^{r_2\Delta}S_{i+1}e^{-r_1\Delta}
+S_ie^{r_1\Delta}S_{i+1}^{-1}e^{-r_2\Delta}-2)
\right]
\end{align}
$\Delta\to 0$の極限をとると$\exp$の肩は
\begin{align}
-\frac{\beta}{2\Delta}\sum_{i=1}^{N-1}(S_i^{-1}e^{r_2\Delta}S_{i+1}e^{-r_1\Delta}
+S_ie^{r_1\Delta}S_{i+1}^{-1}e^{-r_2\Delta}-2)
\xrightarrow{\Delta\to 0}
-\beta\int_0^Td\tau \left(\frac{\partial S(\tau)}{\partial\tau}/S(\tau)+(r_2-r_1)\right)^2
\end{align}
となります。積分を実行すると、$S=S(T)$の満たす確率分布は
\begin{align}
P(S)=\frac{1}{\sigma S\sqrt{2\pi T}}
e^{-\left\{\ln(S/S_0)-(\mu-\sigma^2/2)T\right\}^2/(2\sigma^2T)}
\end{align}
になります。ここで$\mu:=r_2-r_1$。また$\sigma^2:=\beta$は株価(など)の変動の不確定性のパラメータです。ファイナンス理論では$\sigma$はボラティリティ(volatility)と呼ばれます。そして時刻$T$での株価の分布を表す$P(S)$は対数正規分布であり、幾何ブラウン運動における確率変数の従う分布です。例えばWikipediaの
Geometric Brownian motion
の項をご参照ください。幾何ブラウン運動は経済学において為替・株の価格変動を記述するのに頻繁に利用されており、それと無矛盾な結果が導かれました。そしてこれは【公理3】と整合的です。
発展的話題
経済学とゲージ理論に関する発展的な話題に関して触れます。ただし本記事筆者は詳しくは理解しておりませんので、概要を述べるに留めます。興味のある方はIlinski-02Farinelli-01Farinelli-02Farinelli-03Rodriguesをご参照ください。
Black-Scholes方程式との関係
Black-Scholes方程式(BS方程式)は、European call optionと呼ばれる典型的なオプション(※脚注1)に関し、その値動きを記述します。この方程式は変数変換により解析的に解くことができ、その解はBlack-Scholesのオプション価格公式と呼ばれますYamamoto。
Ilinski-02では資産取引のゲージ理論的アプローチとBS方程式との関係を議論しています。この論文では、現金と資産A(例えば株)との取引の他に、現金と他の資産B(例えばデリバティブ)との取引も考えます。そして現金とAの取引によるプラケットと現金とBの取引によるプラケットの相互作用項を作用に導入します:
\begin{align}
s_{\rm gauge}=\sum_{\xi,\zeta}Q_\xi A_{\xi\zeta}Q_\zeta/(2\Delta)
\end{align}
ここで$Q_\xi$は現金と資産$\xi$の取引によるプラケットです。資産Aの価格を$S$、資産Bの価格は時刻と$S$の関数であるとして$C(t,S)$とし、相互作用項から導かれる作用を伊藤の補題により書き直すと以下になりますIlinski-02:
\begin{align}
\beta_2\int dt
\left(
\frac{1}{C}\frac{\partial C}{\partial t}
+\frac{1}{C}\frac{\sigma^2}{2}S^2\frac{\partial^2C}{\partial S^2}
-r_b\left(1-\frac{S}{C}\frac{\partial C}{\partial S}\right)
\right)
\end{align}
ここで$r_b$は銀行預金等安全資産の時間間隔$\Delta$における利率を$e^{r_b\Delta}$のように表した値です(前章の$r_1$に相当する)。この作用の$\beta_2\to 0$の古典極限がBS方程式に対応します:
\begin{align}
\frac{1}{C}\frac{\partial C}{\partial t}
+\frac{1}{C}\frac{\sigma^2}{2}S^2\frac{\partial^2C}{\partial S^2}
-r_b\left(1-\frac{S}{C}\frac{\partial C}{\partial S}\right)=0
\end{align}
ホロノミー, ホモトピーおよびホモロジーとの関係
このようにゲージ理論と資産取引を対応づけることができるなら、ゲージ理論のもつトポロジカルな性質も資産取引に見出したくなります。そして実際に資産取引における幾何学的量・位相不変量や指数定理を見出す試みがなされていますFarinelli-01Farinelli-02。
FarinelliはFarinelli-01において資産取引におけるホロノミーとホモトピーに関して詳しく議論しています。deflator $D_t$(=ある時刻$t$での金融商品の価値を何らかの価値基準により表したもの)及びterm structure $P_{t,s}$(満期が$s$の合成ゼロクーポン債(※脚注2)のある時刻$t$での価格を何らかの資産価格で表した量。資産の将来価格をある価格基準で表した量であり、利益の期間構造を表す)によりゲージ理論(principal fibre bundle)を構成しました。そしてIlinskiの議論の再構築、またこのゲージ理論において定義されるホロノミーと裁定取引の関係およびホモトピー群との関係を議論していてます。例えば、取引の経路が連続的に変形できる場合裁定取引は起こらず、一方連続変形を拒むような障害が存在する場合(例えば年金基金における取引の制限などに由来する障害)その障害を囲むような経路での取引には裁定取引が存在するという議論を行っています。
さらにFarinelli & TakadaFarinelli-02ではホモロジーおよび指数定理に関し議論しています。資産取引における共変微分を定義することでラプラシアンに相当するオペレータを構築し、その固有値ゼロの空間が"No-Free-Lunch-with-Vanishing-Risk"と呼ばれる裁定取引の類似概念の存在する状況であることを示しています。これは指数定理と関係します。また「資産の価格空間」のオイラー特性、さらにキャッシュフローのバンドルのホモロジー群がノンゼロであることは、どちらも"No-Free-Lunch-with-Vanishing-Risk"のトポロジー的障害であることを議論しています。
まとめ
本記事では為替取引また資産取引のゲージ理論的・幾何学的解釈に関して述べました。為替取引における裁定取引の指標はゲージ理論における場の強さやプラケット(またはWilsonループ、数学的にはホロノミー)と対応します。これはリーマン幾何学でいうところの曲率であり、裁定取引が「価値空間の歪み」と解釈できることを示しています。
資産取引においても同様に、2つの資産の取引において同一始点・終点を持つ2つの取引経路の利益の差はプラケットと解釈できます。この場合ゲージ対称性は各資産の各時刻における単位の変更に当たります。ゲージ不変性を含むいくつかの公理のもと、資産価格の変動が満たす確率過程、確率分布を求めることができます。それは幾何ブラウン運動であり、経済学のスタンダードな議論と整合的です。
発展的な話題として、ゲージ理論的な資産価格変動理論とBlack-Scholes方程式との関連、またホロノミー、ホモトピー、ホモロジー及び指数定理などのトポロジカルな概念との関連も議論されています。
本記事で記したゲージ理論的アプローチが実際の市場とどれほど整合的か、またどれほど実際に役立つかは勉強不足でわかりません。しかし物理学や数学分野では、このような応用があることは喜ばしく、また興味深いことであると思います。
おしまい。${}_\blacksquare$
(※脚注1)オプションとは、資産を定められた価格で将来のある時点において売る/買う権利のこと。リスク回避の効果を持つ。例えば株を1万円で購入したのち大暴落して100円になれば大損害を被ります。このようなとき将来9000円で株を売る権利を確保しておけば、暴落しても損害が抑えられます。一方価格が上がれば権利を放棄し普通に市場で売ればよいです。European call optionは満期$T$でのみ権利が行使可能なオプションですYamamoto。
(※脚注2)合成ゼロクーポン債: ゼロクーポン債とは、利子(=クーポン)がないかわりに額面より割り引いて売られ、満期で額面金額が払われる債券。合成ゼロクーポン債とは、他の金融商品を組み合わせて作られた、ゼロクーポン債と同様の働きをもつ債券のこと。
