複素積分で実積分を解く。

積分を解く

どうも、らららです。
複素積分で実積分を求めるのっていいですよね。
今回はそれをやります。

今回の記事の参考にした$\mathfrak{YouTube}$の 動画

解く積分

はい、こちらを解きます。

ここで当たり前ですがすごくありがたいことを書いておきます。
使うので。

虚部と実部を比較するというやつです。
これで計算を楽できるので一応かいておきました。

解く

今回は複素積分で解くので$f(z)$と積分経路を設定していきます。
$f(z)$はそのまま積分する関数で積分経路はバームクーヘンのような経路で積分していきます。
この積分経路で積分を解いているが 記事 あるのでそちらもぜひ(宣伝)
半円の線積分が今回はすべて$0$になるんですがそれは証明せずにやっていきます。
絶対値などで評価していくと$0$になることがわかります。
さぁ解いていきます。

\begin{align} I&=\int_{0}^{\infty}\frac{\log^2x}{\sqrt{x}(1-x)^2}dx \end{align}
$$f(z)=\frac{\log^2x}{\sqrt{z}(1-z)^2}$$

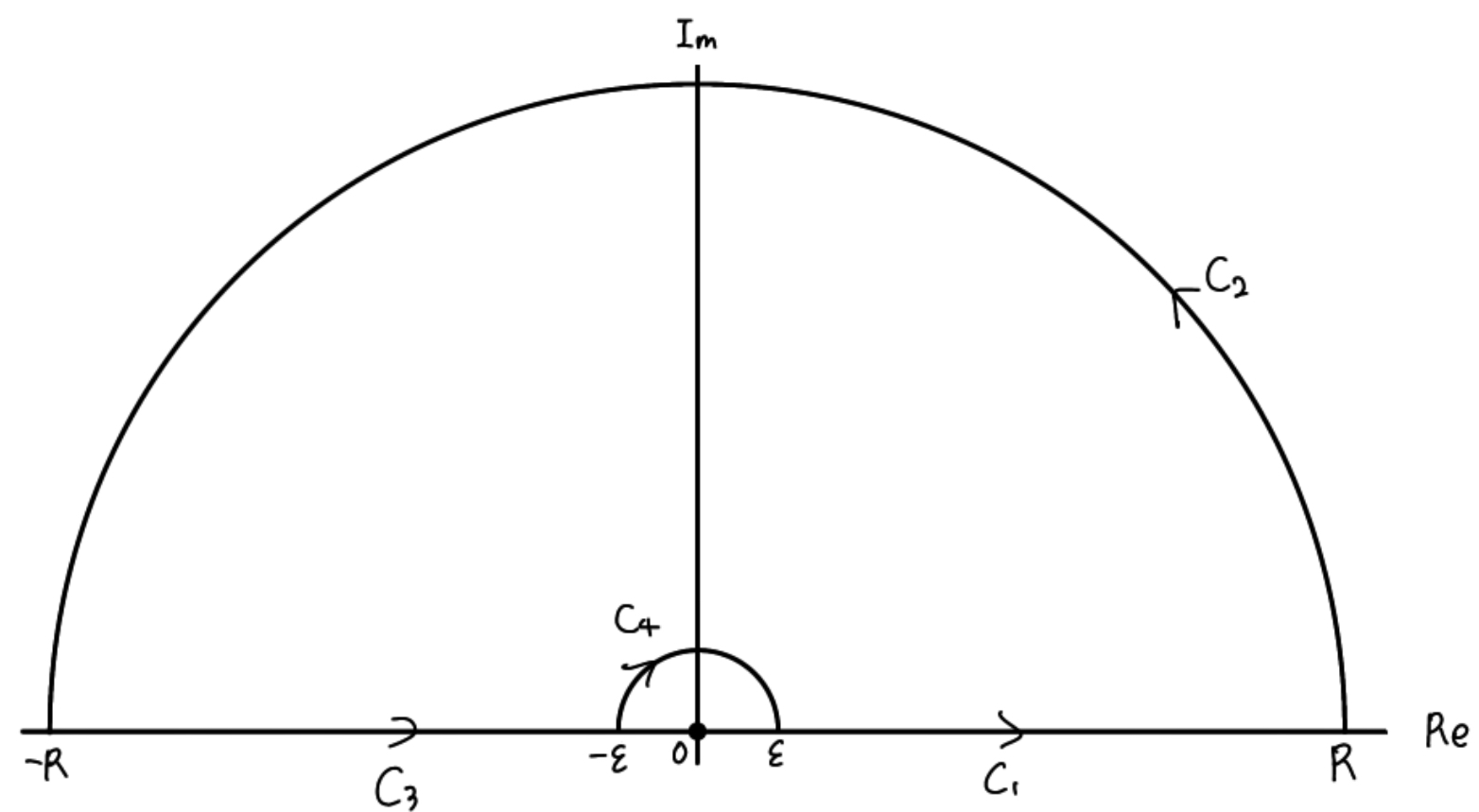積分経路

$$C=C_1+C_2+C_3+C_4$$
$$0=C_1+C_3$$
\begin{align} C_1&=\int_{\ips}^{R}f(x)dx \\&=I\qquad(\ips\to0,R\to\infty) \end{align}
\begin{align} f(-z)&=\frac{\log^2(-z)}{\sqrt{-z}(1+z)^2} \\&=\frac{(\log z+i\pi)^2}{i\sqrt{z}(1+z)^2} \\&=-i\frac{\log^2z}{\sqrt{z}(1+z)^2}+2\pi\frac{\log z}{\sqrt{z}(1+z)^2}+i\pi\frac{1}{\sqrt{z}(1+z)^2} \end{align}
\begin{align} C_2&=\int_{-R}^{-\ips}f(x)dx \\&=\int_{\ips}^{R}f(-x)dx \\&=2\pi\int_{0}^{\infty}\frac{\log x}{\sqrt{x}(1+x)^2}dx+i\left(-\int_{0}^{\infty}\frac{\log^2x}{\sqrt{x}(1+x)^2}+\pi^2\int_{0}^{\infty}\frac{dx}{\sqrt{x}(1+x)^2}\right)\qquad(\ips\to0,R\to\infty) \\&=2\pi I_1+ai\qquad(a\in\mathbb{R}) \end{align}
\begin{align} I_1&=\int_{0}^{\infty}\frac{\log x}{\sqrt{x}(1+x)^2}dx \\&=4\int_{0}^{\infty}\frac{\log x}{(1+x^2)^2}dx \end{align}
$$f(z)=\frac{\log z}{(1+z^2)^2}$$

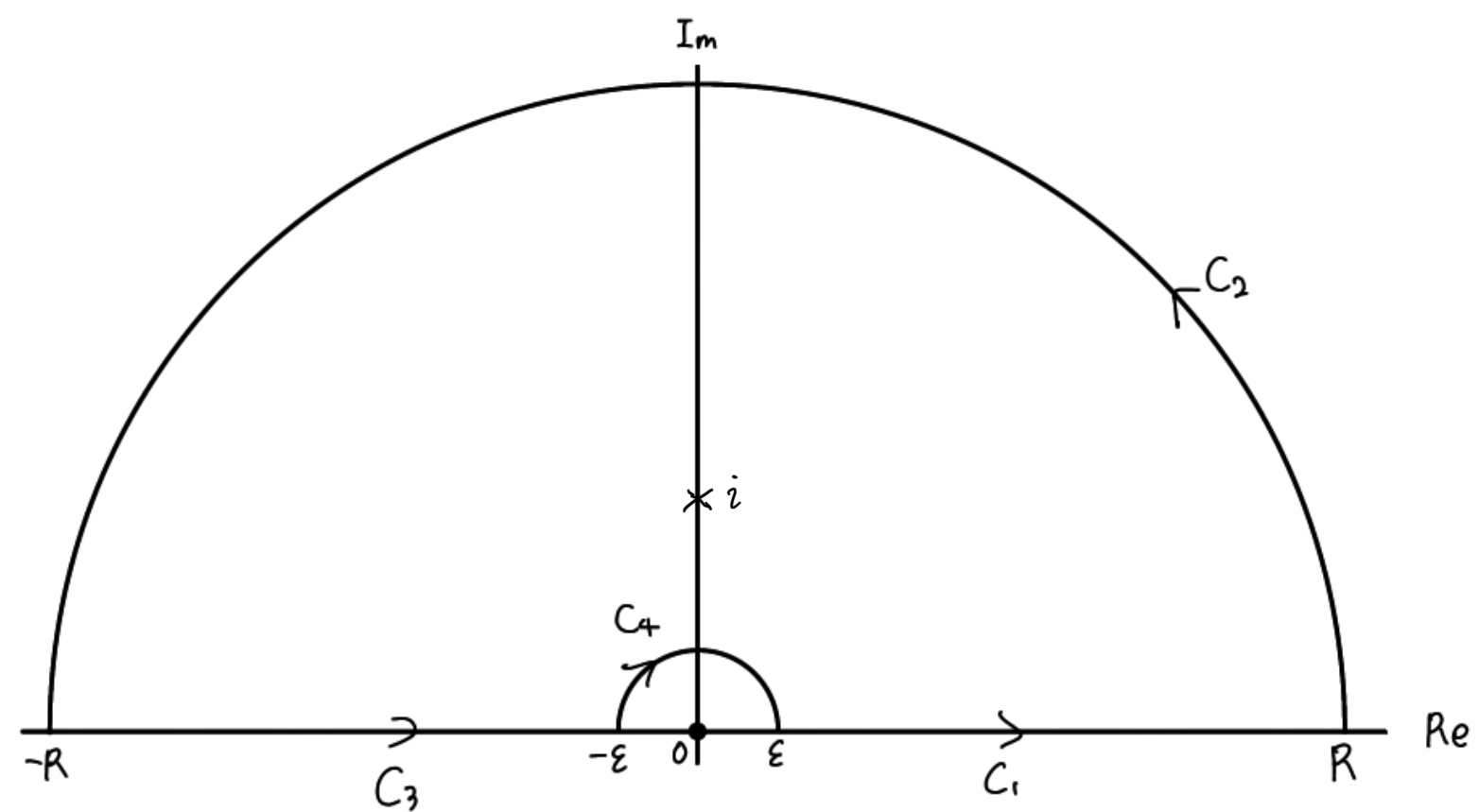積分経路

$$C=C_1+C_2+C_3+C_4$$
$$C=C_1+C_3$$
\begin{align} C_1&=\int_{\ips}^{R}f(x)dx \\&=\frac{1}{4}I_1\qquad(\ips\to0,R\to\infty) \end{align}
\begin{align} f(-z)&=\frac{\log z+i\pi}{(1+z^2)^2} \\&=f(z)+i\pi\frac{1}{(1+z^2)^2} \end{align}
\begin{align} C_2&=\int_{-R}^{-\ips}f(x)dx \\&=\int_{\ips}^{R}f(-x)dx \\&=\int_{\ips}^{R}f(x)dx+i\pi\int_{\ips}^{R}\frac{dx}{(1+x^2)^2} \\&=\frac{1}{4}I_1+bi\qquad(b\in\mathbb{R})(\ips\to0,R\to\infty) \end{align}
$$0=I+2\pi I_1+ai$$
$$I=-2\pi I_1$$
\begin{align} C&=2\pi i\underset{z=i}{\mathrm{Res}}f(z) \\&=2\pi i\lim_{z\to i}\frac{d}{dz}(z-i)^2\frac{\log z}{(z+i)^2} \\&=2\pi i\lim_{z\to i}\frac{\log z}{(z+i)^2} \\&=2\pi i\lim_{z\to i}\frac{i+z-2z\log z}{z(z+i)^3} \\&=2\pi i\frac{i+i-2i\log i}{i(i+i)^3} \\&=-\frac{\pi}2-\frac{\pi}{2}i \end{align}
$$-\frac{\pi}2-\frac{\pi}{2}i=\frac{1}4I_1+\frac{1}4I_1+bi$$
$$I_1=-\pi$$
$$I=-2\pi I_1$$
$$I=2\pi^2$$

でたー！！
$2\pi^2$というキレイな値になりました。
実部を比較するので虚部は計算しなくていいのが楽。
実部を比較するとき虚部は発散しても文字でおいていいです。
$1+\infty i=x$のとき$x=1$
このような感じで実部を比較する分には虚部は発散しても問題はありません。
今回は$f(z)$や$C,C_1,C_2$などを2回使いましたが実際は別のを使う必要があります。
別に混乱しないと思い同じものを使いました。

おしまい！