多様体から入る「位相空間入門」入門

どうも

　こんにちは　ごててんという者です　数学科の学部卒になり就職をしたので、数学を忘れてしまう前に記事を書きたいと思いこの記事を書くに至りました

この記事の効用

　この記事は位相空間論の勉強をスムーズに始めるための記事です　この記事を読んだくらいで位相空間論の基礎が身につくというわけではありませんが、基礎を身につける段階で発生する「こんなことしてなんの意味が......」という気持ちが軽減されると思います

この記事は何をするの？

　位相空間論の勉強をしたい！と思ったことがあれば「多様体」という言葉を聞いたことがある程度あると思います
　多様体の定義には位相空間論の知識が必要となるのですが、この記事は逆に多様体の例を見ることによって位相空間が（道具として）どういうものなのかに迫っていく記事になります

多様体って何

　多様体とは何か、を無茶苦茶適当に書けば、座標が入るなめらかな図形のことです
高校数学までに扱われるものでいえば　直線、曲線、平面とか　そういうものです

　使用する定義にもよるのですが 三角形、直方体、円錐 なども多様体の一種です

（と言いつつ、以下で扱う多様体はすべて境界がないものです）

例1

　多様体の例を一つずつ見ていきましょう　まずはすごく当たり前なものから紹介です　$2$次元座標の平面です　$2$次元ユークリッド空間、$2$次元数空間などと呼ばれます

平面

　なめらか...... のイメージはこの例ではつかないと思います　それは定義をちゃんとしないで話を進めて微妙な感じになっているだけなので安心してください　しかし、座標が入っているというのはわかると思います（これもイメージつかないかも）　座標が入っているどころか、座標そのものですからね

例2

　次はもっといい感じの例を紹介します　多様体といえばこれ！というものです（私がそう思っているだけかもしれませんが）

　その例とは、球面です

球

　球面に座標が入る、というのは想像に難くないのではないでしょうか
　実際は私達は地球の表面に住んでいますが、地球のサイズに対して人間は小さいので　平面のように見えます　という感じに、球面にはいい感じに座標が入ってくれます（実際に多様体として扱うには、適切な仮定のもと数式で表現しなければなりません）

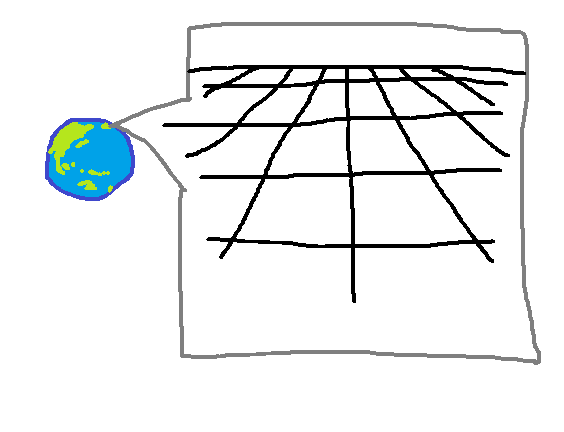お絵かきたのしい

　平面に見える、ということなのでこれは $2$次元の多様体になります

例3

　次をひとまず最後の例とします

　「トーラス」になります

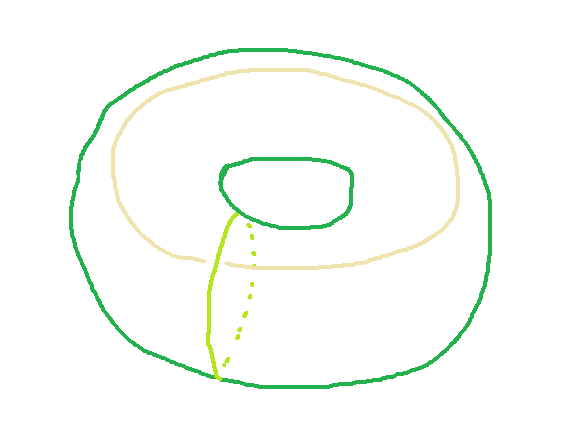中身は詰まっていないものとします

　雑学が好きならこの名前は聞いたことがあると思います　多くのRPGゲームの世界はトーラスの形をしている、みたいな雑学が有名ですね（世界地図の左右と上下が繋がっていると仮定するとこの形になってしまいます）

　これも地表（？）に立てば平面に見えるので$2$次元の多様体です

ええと、この例から何を学べばいいんですか

　高校数学と大学数学をあえて分けるとするならば、次の視点があると思います

　高校数学までで言う球面とは、空間図形の一種の、$3$次元空間の部分集合としての球面という見方だったと思います　しかし、多様体という視点で見ると　球面のニュアンスは少し異なります

　高校数学のこの見方は、$3$次元空間で幾何学をやろうとする過程で球面が出てきた　という感じです

　しかし多様体論は少し違います　多様体論でやろうとしているのは、球面で幾何学をする、ということです

　球面という3次元空間の部分集合では～　という語り口ではなく、　球面の外のことは考えずに球面では～　という語り口で始まります

球面で幾何学をするって何

　大学での幾何学という言葉は多くの意味を持ちます　位相幾何学であったり、代数幾何学であったり、微分幾何学であったり、...... ここでする説明に一番近いのは微分幾何学であると思うのですが、以下そのニュアンスで書きます

　球面で幾何学...... の前に、座標平面での幾何学を軽く振り返ってみます

　大学の解析学では、図形の面積、体積を定義するのに（重）積分を用いたと思います　また偏微分、勾配、回転、発散、ストークスの定理、...... などなど色々ありますね

　さて　説明の準備が整いました　球面で幾何学をする、という言葉の意味なのですが　これは「積分とかストークスの定理とかを、球面の上でもやりたい！！！」ということです

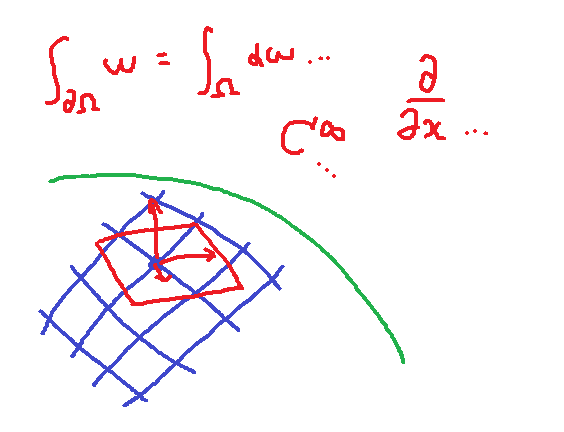それっぽい図

じゃあどうすれば球面で幾何学ができるの？

　問題意識パートは終了です　上では球面としか書いていませんが、もっと言えば上で紹介したトーラスや、曲線など色々なもので幾何学をしたい訳です　そしてそれが多様体の分野としての説明の一部分を与えていると思います

　さて、どうやって幾何学をしていくかなのですが　高校数学までの道具でこれを行うことはできません　そしてここで必要になるのが、「位相空間」です！！！！！！！！！！

ここまでの要約

やっと位相空間編スタート

　一旦、座標平面の話に戻ります　座標平面では「微分」とか「曲線」とか　そういったものを扱っていました　そこでキーワードになっていたものがあると思います

　「近傍」「連続」「収束」「孤立点」などなど、こういったキーワードがありました

　そして位相空間というのは、これらの概念を座標平面以外でやろう！ということです

どうやるの？

　さて、「近傍」「連続」「収束」「孤立点」を一般化するにはどうすれば良いか、という部分なのですが　ここに対する凄まじい答えを位相空間は主張しています　それは次のようなアイデアです

　「開集合」があればこれ全部できるんじゃないですか？

　え～～～　という感じですね　まずは開集合がなんだったかを適当に復習しましょう

開集合ってなんだっけ

　開集合はイメージ的には「境界」のない集合のことです　無限に外側に近づくことができる（が、たどり着くことはできない）感じです

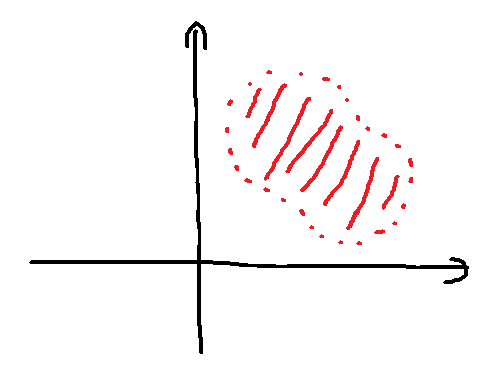こんなの

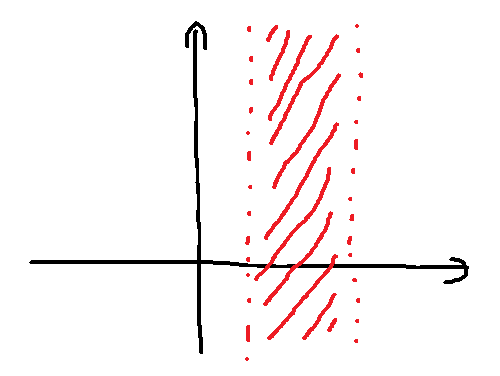こんなの2

座標平面って位相空間的にはどうなの

　もうちょっと数学っぽい表記をしていきます
　いわゆる$2$次元の座標平面を$\mathbb{R}^2$と書きます　そして$2$次元の座標平面の開集合全体の集合を$\mathcal{O}$と書きます

　そして！ このときのこの組$(\mathbb{R}^2,\mathcal{O})$　これが位相空間論的に言う2次元ユークリッド空間です！

　位相空間は「土台となる集合」と、その集合で「開集合と呼ばれるもの」全体のペアのことです！

開集合があれば何ができるの

　開集合があれば何ができるのか　思ったより色々できます　例えば$\epsilon$-$N$論法ができます！　これはつまり、「点列の収束」が定義できます！（位相空間論のレベルだと、収束先が$1$つに定まらない場合も多々あります） 　

　また、近傍の概念を定義することができます　$2$次元の座標平面で言う近傍の条件として、小さい開円盤をとってきて点を覆えるというのがありました

$N$は点$x$の近傍である.

　上の図で$x$を囲んでいるのは開円盤なのですが、円盤である必要はないですね　とにかく開集合で$x$を囲めればいいわけです！

　位相空間は「開集合の全体」を持っているわけですから　近傍の概念を、開集合だけで定義してしまえばいいわけです！

近傍があると何がうれしいんだっけ

　また幾何学の話に戻ります　近傍があるとどういうときに便利なのかですが、例えば微分したいときなどが挙げられます

　今度はたんに$1$次元の数直線で考えます

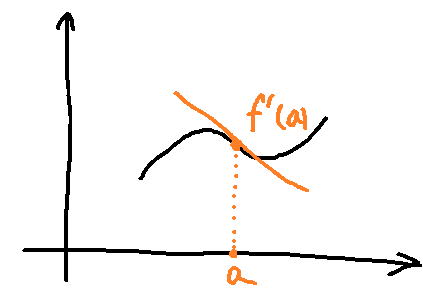微分のイメージ画像ってたいてい極大値も極小値もあるよね

　上の図の関数の「定義域」に注目してみてください

　点$a$で微分をしているのですが、微分は傾きを求める操作なので、そもそも点$a$の近傍で関数が定義されていないと微分ができないわけですね

　一般的に微分をしたいな～と思ったとき　この辺の言葉が整理されているととても便利ということです

まとめとか

　ここまで読んで、開集合さえ定義されていれば幾何学っぽいことができそう！と思っていただけましたでしょうか　少なくとも、「近い」とか「点の周り」とか　そういった議論に強そうだというのはわかっていただけたと思います！

　位相空間の入門書では、この開集合パワーを用いて「閉集合」「閉包」「触点」「内部」「境界」「集積点」「連続写像」「同相」「収束」「極限」「点列連続」「連結」「コンパクト」「等化空間」「ハウスドルフ空間」...... などなど、今までに出てきたものの一般化から空間をさらに詳しく考えるにあたって考え出された概念など、トピック盛りだくさんの議論が展開されます！！！面白そうですね！！！！！

しかし......

　ここまで図とか、そういった直感的なものに頼って位相空間を説明してきました　これで「やるぞ～～～！」と思って位相空間の本を開いても抽象的で苦しいものがあると思います　最初から位相空間を楽しくできる人はそう多くないと思います　私も初めて勉強したときはとても苦痛寄りでした（今はとても好きです）　図形として想像しにくかったり、定義を覚えられなかったり、証明がよくわからなかったり、何がやりたいのかわからなかったり、、、

　学び始めなら、「ユークリッド空間の場合」「離散位相の場合」「密着位相の場合」を考えるだけである程度理解を得ることができると思うので、落ち着いて自分で具体例を適用する時間を取りましょう！

→ 離散位相の「離散」ってなんだよ！！！！！！！！！！！！！！！

　位相空間はやはり勉強コストがそれなりにかかってしまう部分があります　この記事で紹介した位相空間は性質がいいものばかりなので、もっと一般的な、性質がいいとは限らない空間を考えないと存在意義がわからない概念も出てきます　そんなときは、ぼくの別の記事も読んでみると少しは楽しいかもしれません！！！（宣伝）

おわり

　この記事が位相空間の入門にスムーズに繋がってくれたなら嬉しいです　ここまで読んでいただきありがとうございました～