5x5ライツアウトを5x5行列で解く
先日、
勉強中
さんの
ライツアウト(パズルゲーム)について
という記事を拝見し、ライツアウトには線形代数を使った考察があるということを知りました。
線形代数を使った考察ってこんな感じかな?と自分でも考えてみたのですが、調べてみたところ、自分が思いついた方法は他ではあまり使われていませんでした。ということで、記事にしておきます。
よく使われている考え方は、$n\times n$の盤面を$n^2$次元のベクトルと見なし、ボタンを押す操作を$n^2 \times n^2$行列と見なすというものです( 参考文献1 、 参考文献2 )。今回用いる考え方では、$n \times n$の盤面を考えるのに$n \times n$行列を用います。
準備
ライツアウトそのものについての説明は、 しんぎゅらさんの記事 などをご覧ください。ここでは準備として、まずライツアウトのよくある解法を紹介します。
例えば以下のような盤面。

■は光っているマス、□は光っていないマスを表します。全てのライトを消す、すなわち□にすることを目標とします。一番上の段に光っているマスが3つありますが、これらの1つ下のマスを押すと

となり、一番上の段がすべて消えます。同様に、2段目の光っているマスの1つ下、3段目の光っているマスの1つ下、4段目の光っているマスの1つ下を順に押していくと、最終的には

と、一番下の段のみ光っている状態になります。ここまでの操作を下寄せと呼ぶことにしましょう。
ここからは先人の知恵を借ります。一番下の段に残ったマスを見て、一番上の段の適切なボタンを押します。どのボタンを押せば良いかは、例えば
こちらのサイト
などを参照。
今回の例の場合、左から1,4,5番目のボタンを押します。

その後、再度下寄せを行うことにより、ライトがすべて消え、クリアとなります。
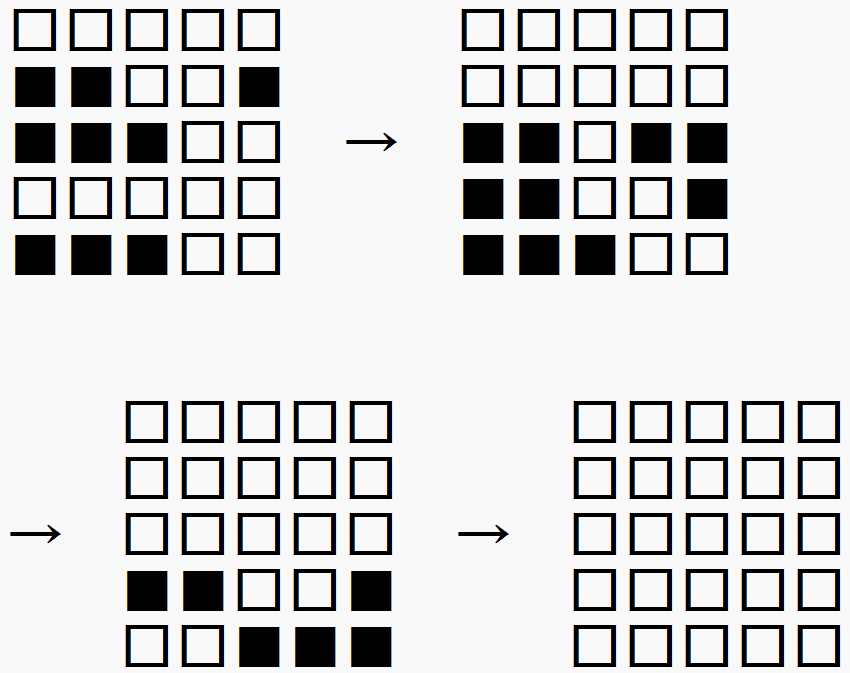
- 下寄せを行う。
- 1番下の段に残ったマスを確認し、1番上の段のボタンを適切に押す。
- 下寄せを行うとクリア。
この解法は対応表に頼ったものとなっていますが、この部分を計算でなんとかしようというのが今回の目標です。
一番下の段のみが光っている状態から、一番上の段のボタンを適切に押して下寄せを行うことで、すべてのライトを消したい。一番上の段のどのボタンを押せば良いかを求めよ。
ところで、計算には行列やベクトルを用います。ベクトルは列ベクトルの方が計算がしやすいので、ライツアウトの盤面においても縦の列を一まとまりで捉えた方が都合が良いです。そこで、上の解法を90°回転させて
- 右寄せを行う。
- 右端の列に残ったマスを確認し、左端の列のボタンを適切に押す。
- 右寄せを行うとクリア。
という向きで考えます。すると問題は
右端の列のみが光っている状態から、左端の列のボタンを適切に押して右寄せを行うことで、すべてのライトを消したい。左端の列のどのボタンを押せば良いかを求めよ。
となります。
ここで、さらに問題を言い換えます。ライツアウトでは、同じ操作を2回行うと元の状態に戻ります。もしある操作によって
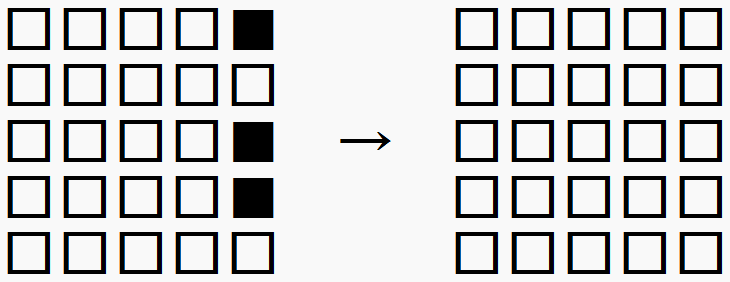
のように右端の列を消すことができるならば、同じ操作によって
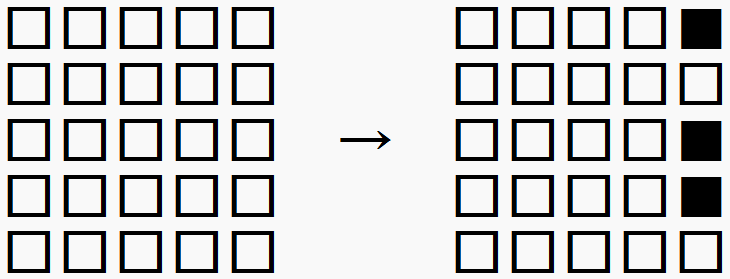
のように、すべてのライトが消えた状態から元の形に戻すことができます。
さらに、右寄せにおいて押すボタンは左から1~4列目の状況で決まるので、最初に押す左端の列のボタンが一致していれば、右端の列の状況によらず右寄せの操作は一致します。
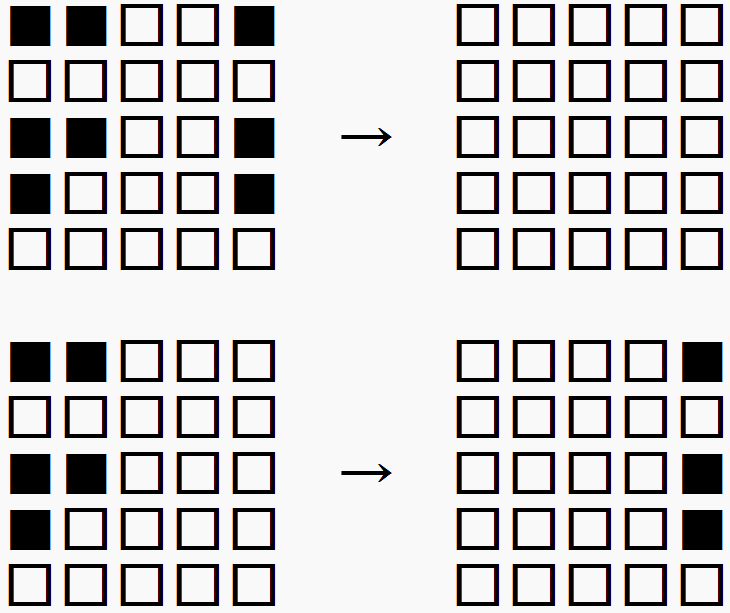 左端の列の同じボタンを押して右寄せすると、押すボタンは一致する
左端の列の同じボタンを押して右寄せすると、押すボタンは一致する
したがって、問題2を考えることは以下の問題と同値です。
全てのライトが消えた状態から、左端の列のボタンをいくつか押して右寄せを行うことにより、右端の列を指定された光り方にできるか?
以下、この問題を考えていきます。
右寄せを式で表す
全てのライトが消えた状態から左端の列のボタンをいくつか押すと、左2列のみが光っている状態になります。ここから右寄せを行う様子を観察すると、例えば

のように、1列ずつ右にずれていく様子が見て取れます。ここで、光っているマスを1,光っていないマスを0として、各列をベクトルと見なします。
$$ \matea 10010, \matea 01100, \mathbf 0, \mathbf 0, \mathbf 0 \quad \to \quad \mathbf 0, \matea 10011, \matea 10010, \mathbf 0, \mathbf 0 \quad \to \quad \mathbf 0, \mathbf 0, \matea 01110, \matea 10011, \mathbf 0$$
このベクトルの変化を式で表しましょう。
$$ \begin{matrix}
\cdots & \bm x & \bm y & \mathbf 0 & \cdots \\
&& \text{↓} &&\\
\cdots & \mathbf 0 & \bm x' & \bm y' & \cdots \\
\end{matrix}$$
と変化するとし、$\bm x', \bm y'$ を $\bm x, \bm y$ で表します。
すぐに分かるのは $\bm y' = \bm x$ ですね。$\bm x$における1の位置の右のボタンが押されるので、さらにその右のボタンが光ります。$\bm x'$については、
$$ \bm x = \matea{x_1}{x_2}{x_3}{x_4}{x_5}, \quad \bm y = \matea{y_1}{y_2}{y_3}{y_4}{y_5}, \quad \bm x' = \matea{x_1'}{x_2'}{x_3'}{x_4'}{x_5'}$$
とおいて考えれば以下の式が得られます。ただし、すべて mod 2 で計算しています。
$$ \begin{aligned}
x_1' &= x_1 + x_2 + y_1\\
x_2' &= x_1 + x_2 + x_3 + y_2\\
x_3' &= x_2 + x_3 + x_4 + y_3\\
x_4' &= x_3 + x_4 + x_5 + y_4\\
x_5' &= x_4 + x_5 + y_5\\
\end{aligned}$$
以降も、行列やベクトルの計算はすべて mod 2 で行うこととします。分かる人向けに言えば、ベクトル、行列はすべて有限体$\mathbb F_2$上で考えます。
行列を用いれば
$$ \bm x' = A\bm x + \bm y, \qquad \text{ ただし } \quad A = \matea{\rowe 11000}{\rowe 11100}{\rowe 01110}{\rowe 00111}{\rowe 00011}$$
と表せます。以下、特に断りのない限り、$A$はこの行列を指すこととします。
ベクトルを繰り返し変化させることを考えます。0,1 からなる5次元列ベクトル $\bm x_1, \bm y_1$ が与えられているとし、
$$ \begin{matrix} \bm x_1 & \bm y_1 & \mathbf 0 & \mathbf 0 & \mathbf 0\\ && \text{↓} &&\\ \mathbf 0 & \bm x_2 & \bm y_2 & \mathbf 0 & \mathbf 0\\ && \text{↓} &&\\ \mathbf 0 & \mathbf 0 & \bm x_3 & \bm y_3 & \mathbf 0\\ && \text{↓} &&\\ && \vdots &&\\ \end{matrix}$$
と変化していくとします。すると漸化式
$$ \bm x_{n+1} = A \bm x_n + \bm y_n, \qquad \bm y_{n+1} = \bm x_n$$
が成り立ちます。$\bm y_{n+1} = \bm x_n$ から$\bm y_n$は消去できますね。そうするとベクトルの変化は
$$ \begin{matrix} \bm x_1 & \bm x_0 & \mathbf 0 & \mathbf 0 & \mathbf 0 \\ && \text{↓} &&\\ \mathbf 0 & \bm x_2 & \bm x_1 & \mathbf 0 & \mathbf 0 \\ && \text{↓} &&\\ \mathbf 0 & \mathbf 0 & \bm x_3 & \bm x_2 & \mathbf 0\\ && \text{↓} &&\\ && \vdots && \end{matrix}$$
となり、漸化式は
$$ \bm x_{n+1} = A \bm x_n + \bm x_{n-1}$$
となります。
問題3を式で表す
全てのライトが消えた状態から考えます。
$$ \begin{matrix}
\mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0
\end{matrix}$$
ここで左端の列のボタンをいくつか押すのですが、この操作は、$\bm x_0 = \mathbf 0$ として
$$ \begin{matrix}
(\bm x_1) & \bm x_0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0
\end{matrix}$$
のように左にもう1列あると見なし、右寄せを1列分だけ行うことと思うことができます。具体的には、例えば左端の列の1,4番目を押すというのは

のように左にもう1列あると考え、右寄せを1列分だけ行うことと同じです。最後まで右寄せを行うと
$$ \begin{matrix}
(\bm x_1) & \bm x_0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \\
&&&\text{↓}&&&\\
& \bm x_2 & \bm x_1 & \mathbf 0 & \mathbf 0 & \mathbf 0 &\\
&&&\text{↓}&&&\\
& \mathbf 0 & \bm x_3 & \bm x_2 & \mathbf 0 & \mathbf 0 &\\
&&&\text{↓}&&&\\
& \mathbf 0 & \mathbf 0 & \bm x_4 & \bm x_3 & \mathbf 0 &\\
&&&\text{↓}&&&\\
& \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm x_5 & \bm x_4 &\\
&&&\text{↓}&&&\\
& \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm x_6 & (\bm x_5) \\
\end{matrix}$$
となります。ここで、ベクトル列 $\{ \bm x_n \}$ は
$$ \bm x_{n+1} = A \bm x_n + \bm x_{n-1}$$
を満たします。最後の$\bm x_6$が指定されたベクトルになるように$\bm x_1$を定めることができるか?というのが今考えている問題です。
すなわち、問題3を言い換えると
0,1からなる5次元列ベクトル$\bm c$が与えられているとする。また、$\bm x_0 = \mathbf 0$ とする。0,1からなるこのとき5次元列ベクトル$\bm x_1$をうまく選んで、
$$ \bm x_{n+1} = A \bm x_n + \bm x_{n-1}$$
によって定まるベクトル列 $\{ \bm x_n \}$ において $\bm x_6 = \bm c$ となるようにできるか?
となります。なお、ここまでの内容は一般サイズのライツアウト(正方形でない長方形でも可)でも同様に考えることができます。
解く
ここからは、上の問題を力技で解いていきます。もっと良い解き方があるかもしれません。
漸化式 $\bm x_{n+1} = A \bm x_n + \bm x_{n-1}$ を繰り返し用いることで、
$$ \begin{aligned}
\bm x_2 &= A \bm x_1\\
\bm x_3 &= (A^2+E)\bm x_1\\
\bm x_4 &= A^3 \bm x_1\\
\bm x_5 &= (A^4 + A^2 + E)\bm x_1\\
\bm x_6 &= (A^5 + A)\bm x_1
\end{aligned}$$
が得られます。さらに$A$のべき乗を計算すると
$$ A^2 = \matea{\rowe 00100}{\rowe 01010}{\rowe 10101}{\rowe 01010}{\rowe 00100} \qquad A^3 = \matea{\rowe 01110}{\rowe 11011}{\rowe 10101}{\rowe 11011}{\rowe 01110}$$
$$ A^4 = A^5 = \matea{\rowe 10101}{\rowe 00000}{\rowe 10101}{\rowe 00000}{\rowe 10101}$$
となります(なんか美しい)。これらを用いて計算すれば
$$ \bm x_6 = \matea{\rowe 01101}{\rowe 11100}{\rowe 11011}{\rowe 00111}{\rowe 10110}\bm x_1$$
が得られます。以上から、解くべき問題は
与えられた$\bm c$に対し、
$$ \matea{\rowe 01101}{\rowe 11100}{\rowe 11011}{\rowe 00111}{\rowe 10110}\bm x_1 = \bm c$$
を満たすような$\bm x_1$を求めよ。
となります。もはやただの連立1次方程式です。
$\bm x_1$にかかっている行列が正則ならば話は早いのですが、残念ながら正則ではないことが確かめられます。仕方がないので掃き出し法で解きます。
$$ \bm c = \matea{c_1}{c_2}{c_3}{c_4}{c_5}$$
とおいて拡大係数行列を行基本変形します。変形結果は一意ではありませんが、例えば
$$ \left(\begin{array}{ccccc|c}
1 & 0 & 0 & 0 & 1 & c_1+c_2 \\
0 & 1 & 0 & 1 & 0 & c_1+c_2+c_3 \\
0 & 0 & 1 & 1 & 1 & c_2+c_3 \\
0 & 0 & 0 & 0 & 0 & c_2+c_3+c_4 \\
0 & 0 & 0 & 0 & 0 & c_1+c_3+c_5
\end{array}\right)$$
となります。このことから、まず条件を満たす$\bm x_1$が存在するためには
$$ c_2 + c_3 + c_4 = 0 \quad \text{ かつ } \quad c_1 + c_3 + c_5 = 0$$
であることが必要十分です。この条件を満たすとき、解は
$$ \bm x_1 = \matea{c_1 + c_2}{c_1 + c_2 + c_3}{c_2+c_3}{0}{0} + t_1\matea 01110 + t_2 \matea 10101 \quad (t_1, t_2 \in \{ 0,1 \})$$
となります。特に、解が4通りあることが分かります。
まとめると、
$\bm c = \matea{c_1}{c_2}{c_3}{c_4}{c_5}$ とするとき、問題5の解が存在するための必要十分条件は
$$ c_2 + c_3 + c_4 = 0 \quad \text{ かつ } \quad c_1 + c_3 + c_5 = 0$$
であることであり、そのときの解は
$$ \bm x_1 = \matea{c_1 + c_2}{c_1 + c_2 + c_3}{c_2 + c_3}{0}{0} + t_1 \matea 01110 + t_2 \matea 10101 \quad (t_1, t_2 \in \{ 0,1 \})$$
である。
となります。
この結果をライツアウトの言葉に直すと、以下の解法が得られます。
- 右寄せを行う。
- 右端の列において、
・「2,3,4番目のマスのうち光っているマスが偶数個か」
・「1,3,5番目のマスのうち光っているマスが偶数個か」
をチェックする。 - (2)の条件を満たしていなければクリア不可能。条件を満たしている場合、右端の列において
・「1,2番目のマスのうち光っているマスが奇数個か」
・「1,2,3番目のマスのうち光っているマスが奇数個か」
・「2,3番目のマスのうち光っているマスが奇数個か」
をチェックし、条件を満たしているかどうかに応じて、左端の列の1,2,3番目のボタンを押す。($i$番目の条件を満たしていれば、$i$番目のボタンを押す) - 右寄せを行うとクリア。
なお、(3) の操作の後、以下のいずれかの操作を行っても良い。
・左端の列の 2,3,4 番目のボタンを押す。
・左端の列の 1,3,5 番目のボタンを押す。
・左端の列の 1,2,4,5 番目のボタンを押す。
少々ややこしいですが、$5 \times 5$ライツアウトの解法を計算によって得ることができました!
また、それぞれの(クリア可能な)盤面に対して解き方が4通り存在することも分かります。ここで「解き方」とは、すべてのライトを消すようなボタンの押し方(押す順番は考慮しない)で、同じボタンを2回以上押さないようなものを指します。
解き方の個数についての説明は詳しくは省略しますが、上の解法における左端の列の押し方をカウントすれば求められることが証明できます。
$3 \times 3$の場合
他のサイズの場合も同様に分析できるので、見てみましょう。
$3 \times 3$の場合、$A = \matcc 110111011$ として、与えられた$\bm c$に対して
$$ \bm x_4 = A^3 \bm x_1 = \bm c$$
を満たす$\bm x_1$を見つけるという問題になります。$A^3$を計算すると
$$ A^3 = \matcc 011111110$$
が得られ、これは正則です。逆行列は
$$ (A^3)^{-1} = \matcc 110111011$$
となるので、$\bm c = \matca{c_1}{c_2}{c_3}$ とおけば
$$ \bm x_1 = (A^3)^{-1} \bm c = \matca{c_1+c_2}{c_1+c_2+c_3}{c_2+c_3}$$
となります。
これにより、以下の解法が得られます。
- 右寄せを行う。
- 右端の列において
・「1,2番目のマスのうち光っているマスが奇数個か」
・「1,2,3番目のマスのうち光っているマスが奇数個か」
・「2,3番目のマスのうち光っているマスが奇数個か」
をチェックし、条件を満たしているかどうかに応じて、左端の列の1,2,3番目のボタンを押す。($i$番目の条件を満たしていれば、$i$番目のボタンを押す) - 右寄せを行うとクリア。
特に、$3 \times 3$ライツアウトはいつでも解くことができ、解き方が1通りであることが分かります。
$4 \times 4$の場合
$4 \times 4$の場合、$A = \matda{\rowd 1100}{\rowd 1110}{\rowd 0111}{\rowd 0011}$ として、与えられた$\bm c$に対して
$$ \bm x_5 = (A^4 + A^2 + E) \bm x_1 = \bm c$$
を満たす$\bm x_1$を見つけるという問題になります。$A^4 + A^2 + E$ を計算すると
$$ A^4 + A^2 + E = O$$
となるので、問題は、与えられた$\bm c$に対して
$$ \mathbf 0 = \bm c$$
を満たす$\bm x_1$を見つけよ、というものになります。すなわち、
・$\bm c = \mathbf 0$ ならば、任意の$\bm x_1$が解となる。
・$\bm c \neq \mathbf 0$ ならば、条件を満たす$\bm x_1$は存在しない。
という結論になります。
ここで、$\bm c = \mathbf 0$ というのは、ライツアウトの言葉で言えば、右寄せを行った段階で既にすべてのライトが消えていることを意味します。というわけで、以下の解法が得られます。
- 右寄せを行う。
- すべてのライトが消えていればその時点でクリア、そうでなければクリア不可能である。
解法としては以上だが、$5 \times 5$ や $3 \times 3$ の場合に無理矢理あわせれば以下のように続けられる。
(3) 全てのライトが消えていれば、左端の列のボタンを任意に押す。
(4) 右寄せを行うとクリア。
$4 \times 4$ライツアウトが簡単であるというのは多くの方が言及していますが、きちんと証明することができました。
$m \times n$の場合
縦$m$マス、横$n$マスのライツアウトを考えます。大したことは書けませんが、思ったことをつらつらと書いていきます。
とりあえず同様に考えていきます。$m$次正方行列$A_m$を
$$ A_m = \begin{pmatrix}
1 & 1 & & & O \\
1 & 1 & 1 & & \\
& 1 & \ddots & \ddots & \\
&&\ddots&\ddots& 1 \\
O&&&1&1
\end{pmatrix}$$
で定めれば、考えるべき問題は
$0,1$からなる$m$次元ベクトル$\bm c$が与えられているとする。また、$\bm x_0 = \mathbf 0$とおく。このとき、$0,1$からなる$m$次元ベクトル$\bm x_1$をうまく与えることで、
$$ \bm x_{k+2} = A\bm x_{k+1} + \bm x_k$$
によって定まるベクトル列$\{ \bm x_k \}$において$\bm x_{n+1}=\bm c$が成り立つようにできるか?
となります。
$5\times 5$ のときに見たように、各$\bm x_n$は
$$ (A_m\text{の多項式})\bm x_1$$
の形で書けます。これをより正確に書くと、
多項式列$\{ f_n(x) \}$を
$$ f_0(x)=0, \quad f_1(x)=1, \quad f_{n+2}(x) = xf_{n+1}(x) + f_n(x)$$
によって定めれば、
$$ \bm x_n = f_{n}(A_m)\bm x_1$$
が成り立つ。
となります。なお、多項式の係数は mod 2 で考えます。これを用いれば、問題6は
$0,1$からなる$m$次元ベクトル$\bm c$が与えられているとき、
$$ f_{n+1}(A_m)\bm x_1 = \bm c$$
を満たす$\bm x_1$を求めよ。
という、連立1次方程式を考える問題と同値になります。ということは結局、$f_{n+1}(A_m)$はどんな行列か?という問題に帰着されるわけですね。
例えば、もし$f_{n+1}(A_m)$が正則なら、どんな$\bm c$に対しても対応する$\bm x_1$がただ1つ存在します。逆に$f_{n+1}(A_m)$が正則でなければ、$\bm c$の取り方によって対応する$\bm x_1$が存在したりしなかったりします。したがって、
(1)$f_{n+1}(A_m)$が正則ならば、どんな初期状態からでもクリア可能である。
(2)$f_{n+1}(A_m)$が正則でないならば、クリア不可能な初期状態が存在する。
と言えます。また、$4 \times 4$の場合を一般化すれば
$f_{n+1}(A_m)=O$のとき、初期状態から右寄せを行っただけですべてのライトが消えればクリア、そうでなければクリア不可能である。
も言えます。
$f_{n+1}(A_m)$の階数を見れば、より詳しく「$f_{n+1}(A_m)\bm x_1 = \bm c$が解を持つような$\bm c$はどのぐらい存在するか」、「解が存在するとすれば、$\bm x_1$の取り方は何通りか」といったことが分かります。
右端の列のみが光っている$2^m$通りの状態のうち、クリア可能なものは$2^{\rank(f_{n+1}(A_m))}$通りであり、それぞれに対して$2^{m-\rank(f_{n+1}(A_m))}$通りの解き方が存在する。
ライツアウトでは、ある状態からの解き方が$k$通りであるならば、すべてのクリア可能な状態からの解き方が$k$通りであることが知られています。したがって、
$m \times n$ライツアウトのある状態がクリア可能ならば、解き方は$2^{m-\rank(f_{n+1}(A_m))}$通り存在する。
ということが分かります。さらに、解き方として取り得るボタンの押し方が$2^{mn}$通りあることから
$m \times n$ライツアウトの$2^{mn}$通りの初期状態うち、クリア可能なものは$2^{mn - m + \rank(f_{n+1}(A_m))}$通りである。
も分かります。
ところで、$m \times n$のライツアウトと$n \times m$のライツアウトは実質同じです。特に、クリア可能な初期状態の個数は同じなので、
任意の正整数$m,n$に対し、
$$ m - \rank(f_{n+1}(A_m)) = n - \rank(f_{m+1}(A_n))$$
が成り立つ。特に、$f_{n+1}(A_m)$が正則であることと$f_{m+1}(A_n)$が正則であることは同値である。
なんてのも成り立ちますね。
一般の$m \times n$の場合に言えることはこんなところでしょうか。$f_{n+1}(A_m)$がどんな行列かがより詳しく分かれば言えることも増えるのでしょうが、なかなか難しそうです。
例えば$1 \times n$ の場合と$n \times 1$の場合を比較してみるなど、話題はまだ色々ありそうですが、長くなってしまったのでこのへんにしておきます。
おまけ
色々検索した結果、雑誌「現代数学」で似たような話が扱われていたのを見つけました。 こちらのページ から見られる一覧表に今回扱ったものと同じ行列が現れています。
おまけ2
$f_{n+2}(x) = xf_{n+1}(x) + f_n(x)$ ってなんかチェビシェフ多項式の漸化式に似てますね。( 参考記事 )
おわりに
ライツアウトについては結構知っているつもりでしたが、今回新たな知見が得られてよかったです。
ではまた