積位相と Borel 集合族

Ref. [Ø]を参考に、以下のような問題を考える。

$T$を適当な集合とし、$T$から$\mathbb{R}^{n}$への函数の集合

\begin{align*} X := (\mathbb{R}^{n})^{T}=\{f:T\to \mathbb{R}^{n}\} \end{align*}

を考える。$\mathbb{R}^{n}$の Borel 集合$F_{t_{i}}\in \mathcal{B}(\mathbb{R}^{n}),\ 1 \leq i \leq k$を用いて$\{f\in X;\ f(t_{i}) \in F_{t_{i}},1 \leq i \leq k\}$と書けるような集合から生成される$\sigma$-加法族$\mathcal{B}$が、$T$の適当な条件のもとで、$X$のある位相についての Borel 集合族となることを以下で見たい。具体的には以下を示したい。（この内容は Ref. [Ø]の主張より弱いが、とりあえず今回はこの弱い主張を確認したい）

函数の集合$X$の積位相

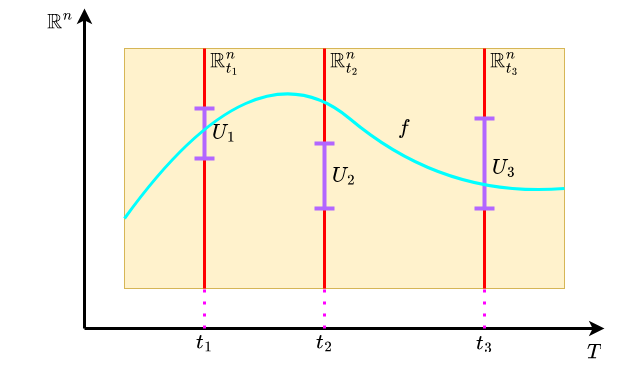
$t \in T$に対して射影$\pi_{t}: (\mathbb{R}^{n})^{T} \to \mathbb{R}^{n}$を$f \mapsto f(t)$で定める。この射影を用いて$X$に積位相を入れる。よって、$t \in T$に対して、準開基は$U_{t} \in \mathcal{O}(\mathbb{R}^{n})$に対する “シリンダー” となる。$f(t)$が属する$\mathbb{R}^{n}$に目印をつけて$\mathbb{R}_{t}^{n}$と書くことにすると、イメージとしては以下のような感じのものになる。

\begin{align*} \pi_{t}^{−1}(U_{t})=(\prod_{t^{\prime} < t}\mathbb{R}_{t^{\prime}}^{n})\times U_{t}\times (\prod_{t^{\prime} > t}\mathbb{R}_{t^{\prime}}^{n}) \end{align*}

積位相の開基はこれらの有限交叉となる。例えば 2 個の準開基の交叉は以下のようになる。

\begin{align*} \bigcap_{i=1}^{2}\pi_{t_{i}}^{−1}(U_{t_{i}})=(\prod_{t^{\prime} < t_{1}}\mathbb{R}_{t^{\prime}}^{n}) \times U_{t_{1}} \times (\prod_{t_{1} < t^{\prime} < t_{2}}\mathbb{R}_{t^{\prime}}^{n})\times U_{t_{2}} \times (\prod_{t^{\prime} > t_{2}}\mathbb{R}_{t^{\prime}}^{n}) \end{align*}

もう少し一般的な書き方をすると、以下のようなものである:

\begin{align*} N(U_{t_{1}}, \cdots, U_{t_{k}}) := \bigcap_{i=1}^{k}\{\pi_{t_{i}}^{−1}(U_{t_{i}});U_{t_{i}} \in \mathcal{O}(\mathbb{R}^{n})\} \tag{1} \end{align*}

位相の（準）開基の可視化

よって、$X=(\mathbb{R}^{n})^{T}$の積位相における開集合は一般に$O = \bigcup N(U_{t_{1}},\cdots, U_{t_{k}})$の形で表現される。この位相は各$\pi_{t},\ t\in T$を連続にする最弱の位相である。

また、この積位相は$X$の函数について「各点収束の位相」とも呼ばれる。つまり、$f_{n} \to f$ in $X$ $\Longleftrightarrow$ $f_{n}(t) \to f(t),\ \forall t \in T$である。(Ref. [F] Prop 4.12)

$\sigma$-加法族

$X$に次のような$\sigma$-加法族を導入する。$\mathbb{R}^{n}$の Borel 集合$F_{t_{i}}\in \mathcal{B}(\mathbb{R}^{n}),\ 1 \leq i \leq k$を用いて

\begin{align*} \{f\in X;f(t_{i})\in F_{t_{i}},1\leq i\leq k\} \tag{2} \end{align*}

と表される集合から生成される$X$上の$\sigma$-加法族を$\mathcal{B}$とする。$T$が第 2 可算公理を満たす時、この$\mathcal{B}$は$X$の積位相についての Borel 集合族になることを見たい。

定理の証明

Eq. (2) を書き換えよう。これは$f\in X$で$t_{1}$, $t_{2}$, $t_{3}$で$U_{1}$, $U_{2}$, $U_{3}$を通るようなものである。これを踏まえると、

\begin{align*} \bigcap_{i=1}^{k}\{\pi_{t_{i}}^{−1}(F_{t_{i}});\ F_{t_{i}} \in \mathcal{B}(\mathbb{R}^{n})\} \tag{3} \end{align*}

と書き直すことができることが分かる。特に$F_{t_{i}} = U_{t_{i}} \in \mathcal{O}(\mathbb{R}^{n}) \subset \mathcal{B}(\mathbb{R}^{n})$をとると、Eq. (1) より$N(U_{t_{1}},\cdots, U_{t_{k}})$に等しい。よって、$\mathcal{B}$は$X$の積位相における開基を含むことが分かった。

ここで、$\bar{\mathcal{B}}$を開基$N(U_{1},\cdots, U_{k})$の集合から生成される最小の$\sigma$-加法族とする。この開基が定める位相が第 2 可算公理を満たす時（後述）、開基の可算個の合併$\bigcup N(U_{1},\cdots, U_{k})$で表現される開集合がすべて$\bar{\mathcal{B}}$に含まれる。つまり$\bar{\mathcal{B}}$は$X$の位相についての Borel 集合族となる。  
ところで、$\mathcal{O}(\mathbb{R}^{n}) \subset \mathcal{B}(\mathbb{R}^{n})$なので、$\bar{\mathcal{B}} \subset \mathcal{B}$である。  
また、Ref. [F] Prop 2.1 より$\mathcal{O}(\mathbb{R}^{n})$の$\pi_{t},\ t\in T$による逆像は$\pi_{t}$の連続性により開集合であり、故に$\bar{\mathcal{B}}$に含まれるので、$\pi_{t}$は$(\bar{\mathcal{B}}, \mathcal{B}(\mathbb{R}^{n}))$-可測である。よって、Eq. (3) またはそれと等価な Eq. (2) のような集合はすべて$\bar{\mathcal{B}}$に含まれる。よって、Eq. (2) の集合から生成される$\sigma$-加法族$\mathcal{B}$は$\mathcal{B} \subset \bar{\mathcal{B}}$ということになる。以上より、$\mathcal{B} = \bar{\mathcal{B}}$である。

最後に、$X$の積位相が第 2 加算公理を満たすことが示されれば、$\mathcal{B}$は Borel 集合であることが分かる。これについては、$\mathbb{R}^{n}$は第 2 加算公理を満たす（c.f. Ref. [U] 例 17.5）ことから、仮定より$T$は可算濃度なので$X = (\mathbb{R}^{n})^{T}$もまた第 2 加算公理を満たすことから従う(c.f. Ref. [F] Section 4.2 Exercise 20, Ref. [K] Chapter 3 Theorem 6 & Problems M)。

例

例えば、$T=[0,∞) \cap \mathbb{Q}$の時、定理が成立する。

まとめ

本の主張よりは弱い形での証明だが、一般的な(？) 開集合に対する Borel 集合族を考えるということをしてこなかったので、良い題材になった。第 2 可算公理も “おまじない” としてしか使っていなかったので、今回比較的ちゃんと向き合うことができて良かった。