ラマヌジャン総和法2:ラマヌジャン和の再定義
はじめに
この記事では 前回の記事 に引き続きラマヌジャンの総和法について勉強していきます。
アベル・プラナの和公式
前回の記事
ではオイラー・マクローリンの和公式
\begin{align}
\sum^b_{n=a}f(n)
=\int^b_af(x)dx+\frac{f(a)+f(b)}2
&+\sum^m_{k=1}\frac{B_{2k}}{(2k)!}(f^{(2k-1)}(b)-f^{(2k-1)}(a))\\
&+\int^b_a\frac{B_{2m+1}(x-\lfloor x\rfloor)}{(2m+1)!}f^{(2m+1)}(x)dx
\end{align}
が重要な役割を果たしていましたが、今回の記事ではまた別の総和公式:アベル・プラナの和公式
$$\sum^b_{n=a}f(n)=\int^b_af(x)dx+\frac{f(a)+f(b)}2
+i\int^\infty_0\frac{f(a+iy)-f(a-iy)-f(b+iy)+f(b-iy)}{e^{2\pi y}-1}dy$$
というものが重要となります。
$a\leq\Re(z)\leq b$における正則関数$f$と$\Re(z)=a,b$において極を持たない有理型関数$g$が
$$\lim_{h\to\infty}\int^{b+ih}_{a+ih}(g(z)+f(z))dz
=\lim_{h\to\infty}\int^{b-ih}_{a-ih}(g(z)-f(z))dz=0$$
を満たすとき$h_\pm(z)=g(z)\pm f(z)$とおくと
$$2\pi i\sum_\a\Res_{z=\a}g(z)
=2\int^b_af(x)dx+i\int^\infty_0(h_+(b+iy)+h_-(b-iy)-h_+(a+iy)-h_-(a-iy))dy$$
が成り立つ。ただし$\a$は$g$の$a<\Re(\a)< b$なる極全体を渡るものとした。
$a\pm ih,b\pm ih$を頂点とする長方形を周る経路$C_h$に対しその上部・下部を$C_h^\pm$とおくと
\begin{align}
\oint_{C_h}g(z)dz
&=\int_{C_h^+}h_+(z)dz+\int_{C_h^-}h_-(z)dz+2\int^b_af(x)dx\\
&\to\int^{i\infty}_0(h_+(b+z)-h_+(a+z))dz\\
&\qquad+\int^0_{-i\infty}(h_-(b+z)-h_-(a+z))dz+2\int^b_af(x)dx\qquad(h\to\infty)\\
&=i\int^\infty_0(h_+(b+iy)-h_+(a+iy))dy\\
&\qquad+i\int^\infty_0(h_-(b-iy)-h_-(a-iy))dz+2\int^b_af(x)dx\\
&=2\pi i\sum_\a\Res_{z=\a}g(z)
\end{align}
とわかる。
$a,b$を整数とし、$a\leq x\leq b$について一様に
$$\lim_{y\to\infty}e^{-2\pi y}f(x\pm iy)=0$$
を満たすような正則関数$f$に対し
$$\sum^b_{n=a}f(n)=\int^b_af(x)dx+\frac{f(a)+f(b)}2
+i\int^\infty_0\frac{f(a+iy)-f(a-iy)-f(b+iy)+f(b-iy)}{e^{2\pi y}-1}dy$$
が成り立つ。
$y>0$に対し
\begin{align}
|-i\cot(x\pm iy)\pm 1|
&=|1-\coth(y\mp ix)|\\
&=\l|\frac{2z^{-1}}{z-z^{-1}}\r|\qquad(z=e^{y\mp ix})\\
&\leq\frac{2e^{-y}}{e^y-e^{-y}}
=e^{-2y}(1+\coth y)
\end{align}
と評価できるので仮定より
$$\lim_{y\to\infty}\int^{b\pm iy}_{a\pm iy}(-i\cot\pi z\pm 1)f(z)dz=0\quad(\mbox{複号同順})$$
が成り立つ。したがって$g(z)=-i\cot(\pi z)f(z)$とおくと上の補題が適用できる。
いま積分経路が$z=a,b$を含むことおよび
$$\Res_{z=n}g(z)=\frac{f(n)}{\pi i}$$
に注意すると
\begin{align}
2\pi i\sum_\a\Res_{z=\a}g(z)
&=2\pi i\sum^b_{n=a}\Res_{z=n}g(z)-\pi i(\Res_{z=a}g(z)+\Res_{z=b}g(z))\\
&=2\sum^b_{n=a}f(n)-(f(a)+f(b))
\end{align}
が成り立ち、また整数$c$に対し
\begin{align}
h_+(c+iy)
&=(-i\cot(i\pi y)+1)f(c+iy)&
h_-(c-iy)
&=(-i\cot(-i\pi y)-1)f(c-iy)\\
&=(1-\coth\pi y)f(c+iy)&
&=-(1-\coth\pi y)f(c-iy)\\
&=-\frac2{e^{2\pi y}-1}f(c+iy)&
&=\frac2{e^{2\pi y}-1}f(c-iy)
\end{align}
が成り立つことから
$$\sum^b_{n=a}f(n)-\frac{f(a)+f(b)}2=\int^b_af(x)dx
+i\int^\infty_0\frac{f(a+iy)-f(a-iy)-f(b+iy)+f(b-iy)}{e^{2\pi y}-1}dy$$
を得る。
オイラー・マクローリンの和公式との関係
ちなみにアベル・プラナの和公式は次のように変形することでオイラー・マクローリンの和公式と直接的に結び付けることができます。
\begin{align} &i\int^\infty_0\frac{f(a+iy)-f(a-iy)-f(b+iy)+f(b-iy)}{e^{2\pi y}-1}dy\\ ={}&\sum^\infty_{n=1}\frac{B_{2n}}{(2n)!}(f^{(2n-1)}(b)-f^{(2n-1)}(a)) \end{align}
$$f(c+z)=\sum^\infty_{n=0}\frac{f^{(n)}(c)}{n!}z^n$$
とテイラー展開したとき
$$f(c+z)-f(c-z)=\sum^\infty_{n=0}\frac{f^{(2n-1)}(c)}{(2n-1)!}z^{2n-1}$$
が成り立ち、またゼータ関数の積分表示と特殊値
\begin{align}
\z(s)&=\frac1{\G(s)}\int^\infty_0\frac{x^{s-1}}{e^x-1}dx\\
\z(2n)&=(-1)^{n-1}\frac{(2\pi)^{2n}}{(2n-1)!}\frac{B_{2n}}{4n}
\end{align}
から
$$\int^\infty_0\frac{x^{2n-1}}{e^{2\pi x}-1}dx=(-1)^{n-1}\frac{B_{2n}}{4n}$$
が成り立つことに注意すると
\begin{align}
i\int^\infty_0\frac{f(c+iy)-f(c-iy)}{e^{2\pi y}-1}dy
&=2i\sum^\infty_{n=0}\frac{f^{(2n-1)}(c)}{(2n-1)!}i^{2n-1}\int^\infty_0\frac{y^{2n-1}}{e^{2\pi y}-1}dy\\
&=\sum^\infty_{n=0}\frac{f^{(2n-1)}(c)}{(2n-1)!}(-1)^n2\cdot(-1)^{n-1}\frac{B_{2n}}{4n}\\
&=-\sum^\infty_{n=0}\frac{B_{2n}}{(2n)!}f^{(2n-1)}(c)
\end{align}
とわかる。
ラマヌジャン和の再定義
さて
前回の記事
で考えた総和法では
$$\l|\int^\infty_1B_{2m+1}(\{x\})f^{(2m+1)}(x)dx\r|<\infty$$
という条件が必要なのでした。
ただこの条件はかなり限定的であり、あまり有用でありません。例えば$\sum e^n$のように何回微分しても急速に増大する関数の総和を考えることはできません。しかしラマヌジャン総和法を適当な方法で抽象化し、その総和可能性を拡大することで上のような級数にも
$$\sum^\R_{n\geq1}e^n=-\frac{e^2}{e-1}$$
のような値を与えることができます。
差分方程式と$C_1(f)$の表示
ラマヌジャンの記述に基づくと
\begin{align}
\phi(x)=C_1(f)+\int^x_1f(t)dt
&+\frac{f(x)}2+\sum^m_{k=1}\frac{B_{2k}}{(2k)!}f^{(2k-1)}(x)\\
&-\int^\infty_x\frac{B_{2m+1}(\{t\})}{(2m+1)!}f^{(2m+1)}(t)dt
\end{align}
という関数は
$$\phi(x)-\phi(x-1)=f(x)\qquad(\phi(0)=0)$$
という方程式を満たすのでした。
ここでこの方程式を積分することで
$$\int^n_1f(x)dx=\int^n_1(\phi(x)-\phi(x-1))dx=\int^n_{n-1}\phi(x)dx-\int^1_0\phi(x)dx$$
が成り立つので漸近的に
$$\int^n_{n-1}\phi(x)dx\sim\phi(n)$$
とみなせること、および
$$f^{(k)}(n)\to0\quad(n\to\infty)$$
となることを仮定すると
$$C_1(f)
=\lim_{n\to\infty}\l(\phi(n)-\int^n_1f(x)dx\r)
=\int^1_0\phi(x)dx$$
という表示が得られます。
特に
\begin{align}
R(x)&=C_1(f)+f(x)-\phi(x)\\
&=C_1(f)-\phi(x-1)
\end{align}
とおくとラマヌジャン和は以下のように再定義することができます。
$$R(x)-R(x+1)=f(x)$$
かつ
$$\int^2_1R(x)dx=0$$
を満たすような関数$R(x)$に対し、その$x=1$における値$R(1)$のことを級数$\sum f(n)$のラマヌジャン和と言い
$$R(1)=\sum^\R_{n\geq1}f(n)$$
と表す。
基本定理
まず上のような関数$R(x)$の存在と一意性が保証される条件について考えておきましょう。
以下ある$\d,\e,C>0$が存在し$\Re(z)>1-\d$において正則かつ
$$|g(z)|\leq Ce^{(\a-\e)|z|}$$
を満たすような関数$g$全体の集合を$\O^\a$とおきます。
$R\in\O^{2\pi}$が
$$R(x)-R(x+1)=0,\quad\int^2_1R(x)dx=0$$
を満たすとき$R=0$が成り立つ。
周期性より$R$は$\C$全体に解析接続でき、特に
$$S(z)=R\l(\frac1{2\pi i}\log z\r)$$
とおくとこれは$\C\setminus\{0\}$上で正則関数を定める。
いま$S$を$z=0$の周りでローラン展開することによって
$$R(x)=S(e^{2\pi ix})=\sum^\infty_{n=-\infty}c_ne^{2\pi inx}$$
とフーリエ級数展開でき、$R\in\O^{2\pi}$に注意して$\Im(x)\to\pm\infty$における挙動を考えることで$n\neq0$に対し$c_n=0$となることがわかる。これは
$$c_n=\frac1{2\pi i}\int_{|z|=r}\frac{S(z)}{z^{n+1}}dz
=\frac1{2\pi r^n}\int^{2\pi}_0S(re^{i\t})e^{-in\t}d\t$$
を直接評価し$r\to0,\infty$とすることでもわかる。
したがって$R=c_0$であり
$$c_0=\int^2_1R(x)dx=0$$
より$R=0$を得る。
$f\in\O^\a\;(\a\leq2\pi)$に対しある$R\in\O^\a$が一意に存在し
$$R(x)-R(x+1)=f(x),\quad\int^2_1R(x)dx=0$$
が成り立つ。特に
$$R(x)=-\int^x_1f(t)dt+\frac{f(x)}2+i\int^\infty_0\frac{f(x+it)-f(x-it)}{e^{2\pi t}-1}dt$$
と表せる。
$R$が一意的であることは方程式の線形性と上の補題からわかり、また
$$R(x)=-\int^x_1f(t)dt+\frac{f(x)}2+i\int^\infty_0\frac{f(x+it)-f(x-it)}{e^{2\pi t}-1}dt$$
が$R\in\O^\a$を満たすことは簡単にわかる。したがってあとはこれが
$$R(x)-R(x+1)=f(x),\quad\int^2_1R(x)dx=0$$
を満たすことを示せばよい。
いまアベル・プラナの和公式に注意すると
\begin{align}
R(x)-R(x+1)
&=\int^{x+1}_xf(t)dt+\frac{f(x)-f(x+1)}2+i\int^\infty_0\frac{f(x+it)-f(x-it)-f(x+1+it)+f(x+1-it)}{e^{2\pi t}-1}dt\\
&=(f(x+1)+f(x))-f(x+1)\\
&=f(x)
\end{align}
がわかり、また
$$F(x)=\int^x_1f(t)dt$$
とおくと再びアベル・プラナの和公式により
\begin{align}
\int^2_1R(x)dx
&=-\int^2_1F(x)dx+\frac{F(2)}2
+i\int^\infty_0\frac{F(2+it)-F(2-it)-F(1+it)+F(1-it)}{e^{2\pi t}-1}dt\\
&=F(2)+\frac{F(1)}2-(F(2)+F(1))\\
&=-\frac{F(1)}2\\
&=0
\end{align}
を得る。
以上により関数$f\in\O^{2\pi}$に対しそのラマヌジャン定数$R(1)$が一意的に存在することがわかりました。
しかし例えば$f(x)=\sin\pi x$とおくと
$$\frac{\sin\pi x}2-\frac{\sin\pi(x+1)}2=\sin\pi x$$
が成り立つことから$R$の一意性より
$$R(x)=\frac{\sin\pi x}2-\int^2_1\frac{\sin\pi t}2dt
=\frac{\sin\pi x}2+\frac1\pi$$
つまり
$$\sum^\R_{n\geq1}\sin\pi n=\frac1\pi$$
と求まることになりますが、これは明らかに
$$\sum^\R_{n\geq1}0=0$$
であることに整合しません。
したがって関数$f$の取り方に依らず級数$\sum f(n)$の和を定めるにはもう少し制限を掛ける必要があります。そのためには以下の定理が役に立ちます。
$f\in\O^\pi$が任意の$n\geq1$に対し$f(n)=0$を満たすとき、恒等的に$f=0$が成り立つ。
Ramanujan's Master Theorem
より$\phi\in\O^\pi$に対し
$$\Phi(x)=\frac1{2\pi i}\int^{c+i\infty}_{c-i\infty}\frac\pi{\sin\pi s}\phi(1-s)x^{-s}ds$$
とおくと$x=0$の近傍で
$$\Phi(x)=\sum^\infty_{n=0}\phi(1+n)(-x)^n$$
が成り立ち、またある領域において
$$\phi(1-s)=\frac{\sin\pi s}\pi\int^\infty_0\Phi(x)x^{s-1}dx$$
と表せることに注意するとわかる。
$f,g\in\O^\pi$が$n\geq1$に対し$f(n)=g(n)$を満たすとき、恒等的に$f=g$が成り立つ。
まとめ
以上より一般のラマヌジャン和は以下のように定義できることになります。
級数$\sum a_n$がラマヌジャン総和可能であるとは$f(n)=a_n$なる$f\in\O^\pi$が存在することを言い、このとき
$$\sum^\R_{n\geq1}a_n:=\frac{f(1)}2+i\int^\infty_0\frac{f(1+it)-f(1-it)}{e^{2\pi t}-1}dt$$
と定まる値のことをラマヌジャン和と言う。
また上のような$f$に対し
$$R(x)-R(x+1)=f(x),\quad\int^2_1R(x)dx=0$$
なる$R\in\O^\pi$が一意に存在し、その$x=1$における値
$$R(1)=\sum^\R_{n\geq1}a_n$$
としてもラマヌジャン和は定められる。
このとき
$$\sum^n_{k=1}f(k)=R(1)+\int^n_1f(x)dx+\frac{f(n)}2
-i\int^\infty_0\frac{f(n+iy)-f(n-iy)}{e^{2\pi y}-1}dy$$
が成り立つことに注意しましょう。オイラー・マクローリンの和公式を用いた定義
\begin{align}
\sum^n_{k=1}f(k)
=C_1+\int^n_1f(x)dx+\frac{f(n)}2
&+\sum^m_{k=1}\frac{B_{2k}}{(2k)!}f^{(2k-1)}(n)\\
&-\int^\infty_n\frac{B_{2m+1}(\{x\})}{(2m+1)!}f^{(2m+1)}(x)dx
\end{align}
と比較すると自然な一般化になっていることがわかりますね。
基本性質
さてようやくラマヌジャン和の決定版が完成したのでまずはこの性質について見ていきましょう。
なおいくつかの主張に関しては
前回の記事
と同様にして示せるのでその証明は省略します。
$$\sum^\R_{n\geq1}(af(n)+bg(n))=a\sum^\R_{n\geq1}f(n)+b\sum^\R_{n\geq1}g(n)$$
$x\in\mathbb{R}$に対し$f(x)\in\mathbb{R}$となるとき
$$\sum^\R_{n\geq1}f(n)\in\mathbb{R}$$
が成り立つ。
鏡像の原理より$f(\ol z)=\ol{f(z)}$つまり
$$f(1+it)-f(1-it)=2i\Im f(1+it)$$
が成り立つことに注意するとわかる。
$x\in\mathbb{R}$に対し$f_r(x)=\Re f(x),f_i=\Im f(x)$を満たすような関数$f_r,f_i\in\O^\pi$が存在するとき
\begin{align}
\Re\l(\sum^\R_{n\geq1}f(n)\r)&=\sum^\R_{n\geq1}\Re f(n)\\
\Im\l(\sum^\R_{n\geq1}f(n)\r)&=\sum^\R_{n\geq1}\Im f(n)
\end{align}
が成り立つ。
$$\sum^\R_{n\geq1}f(n)=\sum^\R_{n\geq1}f(n+1)+f(1)-\int^2_1f(x)dx$$
アベル・プラナの和公式、あるいは
$$S(x)-S(x+1)=f(x+1),\quad\int^2_1S(x)dx=0$$
なる関数として
\begin{align}
S(x)&=R(x+1)-\int^2_1R(t+1)dt\\
&=R(x)-f(x)+\int^2_1f(t)dt
\end{align}
が取れることに注意するとわかる。
$$\lim_{n\to\infty}\int^\infty_0\frac{f(n+iy)-f(n-iy)}{e^{2\pi y}-1}dy=0$$
が成り立つとき
$$\sum^\R_{n\geq1}f(n)=\lim_{n\to\infty}\l(\sum^n_{k=1}f(k)-\int^n_1f(x)dx-\frac{f(n)}2\r)$$
$\sum^\infty_{n=1}f(n),\int^\infty_1f(x)dx$がそれぞれ収束するとき
$$\sum^\R_{n\geq1}f(n)=\sum^\infty_{n=1}f(n)-\int^\infty_1f(x)dx$$
特に$\sum^\infty_{n=0}f(x+n)$が収束するとき
$$R(x)=\sum^\infty_{n=0}f(x+n)-\int^\infty_1f(t)dt$$
計算例
$f(x)=e^{-zx}$とおくと$f\in\O^\pi$であることと$z$が下図のような領域$U_\pi$に含まれることは等価であり
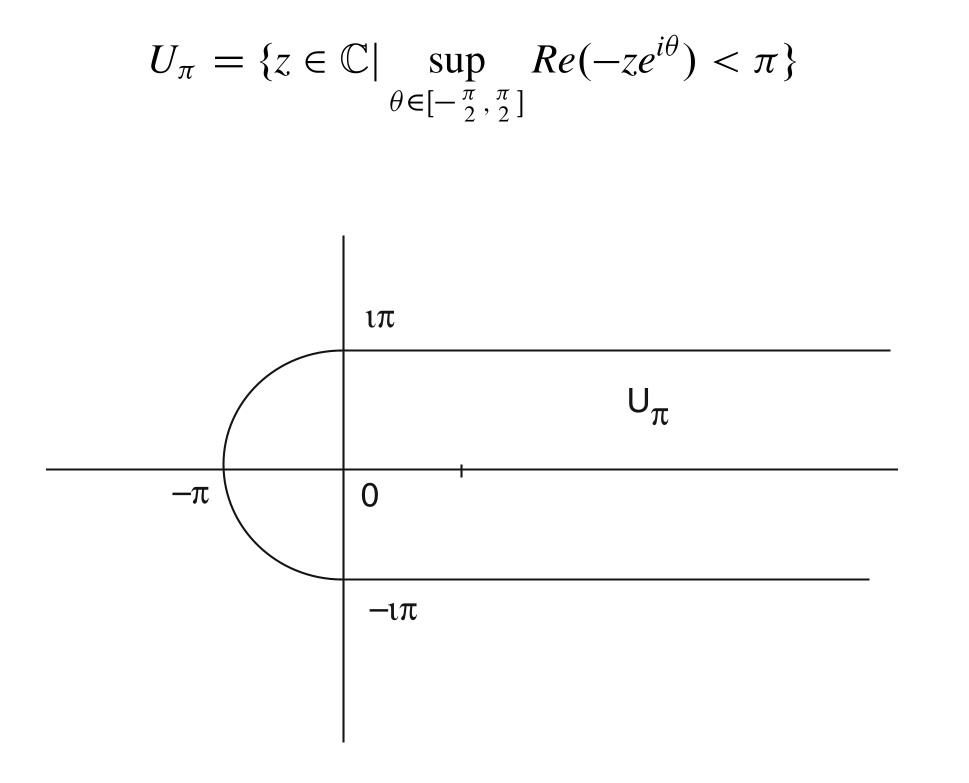
このとき
$$\frac{e^{-zx}}{1-e{-z}}-\frac{e^{-z(x+1)}}{1-e^{-z}}=e^{-zx}$$
より
\begin{align}
R(x)&=\frac{e^{-zx}}{1-e^{-z}}-\int^2_1\frac{e^{-zt}}{1-e^{-z}}dt\\
&=\frac{e^{-zx}}{1-e^{-z}}-\frac{e^{-z}}z
\end{align}
つまり
$$\sum^\R_{n\geq1}e^{-zn}=\frac{e^{-z}}{1-e^{-z}}-\frac{e^{-z}}z$$
と求まる。
特に$z=-1$や$z=it$とすることで
\begin{align}
\sum^\R_{n\geq1}e^n&=-\frac{e^2}{e-1}\\
\sum^\R_{n\geq1}\cos nt&=-\frac12+\frac{\sin t}t\\
\sum^\R_{n\geq1}\sin nt&=\frac12\cot\frac t2-\frac{\cos t}t
\end{align}
などが得られる。
$f(x)=x^k$とおくと
$$\frac{te^{t(x+1)}}{e^t-1}-\frac{te^{tx}}{e^t-1}=te^t$$
の両辺における$t^{k+1}$の係数を比較することで得られるベルヌーイ多項式の性質
$$\frac{B_{k+1}(x+1)}{k+1}-\frac{B_{k+1}(x)}{k+1}=x^k$$
から
\begin{align}
R(x)
&=-\frac{B_{k+1}(x)}{k+1}+\int^2_1\frac{B_{k+1}(x)}{k+1}dx\\
&=-\frac{B_{k+1}(x)}{k+1}+\int^2_1\l(\frac{B_{k+1}(x-1)}{k+1}+(x-1)^k\r)dx\\
&=-\frac{B_{k+1}(x)}{k+1}+\l[\frac{B_{k+2}(x)}{(k+1)(k+2)}+\frac{x^{k+1}}{k+1}\r]^1_0\\
&=-\frac{B_{k+1}(x)}{k+1}+\frac1{k+1}
\end{align}
つまり
$$\sum^\R_{n\geq1}n^k=\z(-k)+\frac1{k+1}$$
と求まる。
$f(x)=1/x$とおくとディガンマ関数
$$\psi(z)=\frac{d}{dz}\log\G(z)$$
の性質
$$\psi(z+1)-\psi(z)=\frac1z$$
から
\begin{align}
R(x)&=-\psi(x)+\int^2_1\psi(t)dt\\
&=-\psi(x)+[\log\G(t)]^2_1\\
&=-\psi(x)
\end{align}
つまり$\psi(1)=-\g$に注意すると
$$\sum^R_{n\geq1}\frac1n=\g$$
と求まる。
$f(x)=1/x^s\;(\Re(s)>1)$とおくとフルヴィッツのゼータ関数
$$\z(s,x)=\sum^\infty_{n=0}\frac1{(n+x)^s}$$
によって
\begin{align}
R(x)
&=\z(s,x)-\int^\infty_1\frac1{t^s}dt\\
&=\z(s,x)-\frac1{s-1}\\
\end{align}
つまり$\z(s,1)=\z(s)$に注意すると
$$\sum^\R_{n\geq1}\frac1{n^s}=\z(s)-\frac1{s-1}$$
と求まる。
また
\begin{align}
f(x+it)-f(x-it)
&=-\frac{(x+it)^s-(x-it)^s}{(x^2+t^2)^s}\\
&=-2i\frac{\sin(s\arctan(t/x))}{(x^2+t^2)^{s/2}}
\end{align}
より
$$R(x)=\frac{x^{1-s}-1}{s-1}+\frac{x^{-s}}2
+2\int^\infty_0\frac{\sin(s\arctan(t/x))}{(x^2+t^2)^{s/2}}\frac{dt}{e^{2\pi t}-1}$$
と表せ、これは$s$について$\C$全体で正則関数を定めるので
$$\sum^\R_{n\geq1}\frac1{n^s}=\z(s)-\frac1{s-1}$$
は任意の$s\in\C$に対し成り立つことになる。
$f(x)=\log x$とおくと
$$\log\G(x+1)-\log\G(x)=\log x$$
より
$$R(x)=-\log\G(x)+\int^2_1\log\G(t)dt$$
と表せ、また
$$\int^2_1\log\G(x)dx=\frac12\log2\pi-1$$
となることが知られているので
$$\sum^\R_{n\geq1}\log n=\frac12\log2\pi-1$$
と求まる。
