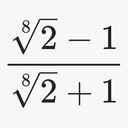ゼータ関数の収束を速める

ゼータ関数

とし、$\zeta(s,z)$や$\Phi(-1,s,z)$を効率良く計算する方法を模索します。

方法1: オイラー積

オイラー積 Wikipedia
$p\in\P$
$\displaystyle \zeta(s) = \prod_p\frac1{1-p^{-s}}$や、$\displaystyle　\beta(s) = \prod_{p\ge3}\frac1{1-(-1)^{\frac{p-1}2}p^{-s}}$を用いれば、収束が速まることが期待できます。
例としてリーマンゼータ関数について考えましょう。
今、$P\in\Pとし、$
$\beginend{align}{ S(P) \acoloneqq \sum_{1\le n\le P}n^{-s} \\ T(P) \acoloneqq \prod_{p\le P}\frac1{1-p^{-s}} }$
とした時、$T(P)$を展開すれば、
$\displaystyle T(P) = \sum_{n'\ge1\ \land\ \forall p>P(p\ |\not\ n')}{n'}^{-s} \quad\text{※$n'$は素因数が全て$P$以下。}$
となるため、$T(P)$は$S(P)$よりも遥かに多くの項を足していることになります。

誤差

例として$s=2,P=5$の場合の誤差を計算すれば、
$\beginend{alignat}{2 \zeta(2)-S(5) &= \frac{\pi^2}6-\lr({\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}}) &&= 0.181322\cdots \\ \zeta(2)-T(5) &= \frac{\pi^2}6-\frac1{\lr({1-\frac14})\lr({1-\frac19})\lr({1-\frac1{25}})} &&= 0.082434\cdots }$
となり、それなりに加速されていることが確認できます。

方法2: 最後の項を$2$で割る

交代級数である時、最後の項を$2$で割ることで加速できます。
$\{a_n\}$は単調減少かつ常に正でその交代和が収束するものとし、
$\beginend{align}{ s_N \acoloneqq \sum_{n=1}^N(-1)^{n-1}a_n \\ t_N \acoloneqq \frac{s_N+s_{N+1}}2 = s_N + \frac{(-1)^Na_{N+1}}2 }$
を考えます。この時、$t_N$は$s_N$よりも速く$s_\infty$に収束する場合があります。
左：加速される場合($s_N$の収束がさほど速くない。)
右：加速されない場合($s_N$の収束が速い。)

誤差

$\beginend{align}{ S(N) \acoloneqq \sum_{n=1}^N n^{-2} \\ T(N) \acoloneqq \sum_{n=1}^N n^{-2} + \frac{(N+1)^{-2}}{2} }$
$\beginend{alignat}{2 \Phi(-1,2,1)-S(5) &= \frac{\pi^2}{12}-\lr({\frac11-\frac14+\frac19-\frac1{16}+\frac1{25}}) &&= -0.016144\cdots \\ \Phi(-1,2,1)-T(5) &= \frac{\pi^2}{12}-\lr({\frac11-\frac14+\frac19-\frac1{16}+\frac1{25}-\frac1{2\cdot36}}) &&= -0.002255\cdots }$

方法3: 加速法

汎用性の高い エイトケンのΔ2乗加速法(Wikipedia) を用いて加速することもできます。
また、これは重ね掛けや他の方法との併用ができます。

級数に$1$回適用する場合、$\displaystyle s_n := \sum_{k=m}^n a_k$として、
$\beginend{align}{ t_n \acoloneqq s_n - \frac{(s_{n+1}-s_n)^2}{s_{n+2}-2s_{n+1}+s_n} = s_n - \frac{(s_{n+1}-s_n)^2}{(s_{n+2}-s_{n+1})-(s_{n+1}-s_n)} \\&= s_n - \frac{a_{n+1}^2}{a_{n+2}-a_{n+1}} = s_n + \frac{a_{n+1}^2}{a_{n+1}-a_{n+2}} \\ s_\infty &= t_\infty = \lim_{n\to\infty}\lr( {\sum_{k=m}^n a_k + \frac{a_{n+1}^2}{a_{n+1}-a_{n+2}}}) }$
となります。

誤差

$\beginend{align}{ S(N) \acoloneqq \sum_{n=1}^N n^{-2} \\ T(N) \acoloneqq \sum_{n=1}^N n^{-2} + \frac{(N+1)^{-4}}{(N+1)^{-2}-(N+2)^{-2}} = \sum_{n=1}^N n^{-2} + \frac{(N+2)^2}{(N+1)^2[(N+2)^2-(N+1)^2]} \\&= \sum_{n=1}^N n^{-2} + \frac1{2N+3}\lr({\frac{N+2}{N+1}})^2 }$
$\beginend{alignat}{2 \zeta(2)-S(5) &= \frac{\pi^2}6-\lr({\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}}) &&= 0.181322\cdots \\ \zeta(2)-T(5) &= \frac{\pi^2}6-\lr[{\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}+\frac1{13}\lr({\frac76})^2}] &&= 0.076622\cdots }$

方法4: 漸近級数

ベルヌーイ多項式やオイラー多項式 を用いるとかなり加速できます。

$a$は基本何でもいいですが、$\displaystyle \frac12$を代入すると奇数番目の項が消えて、
$\displaystyle N'=\lr\lfloor{\frac N2}\rfloor$
$\beginend{align}{ \zeta(s,z) &= \lim_{M\to\infty} \lr[{\sum_{m=0}^{M-1}(z+m)^{-s} + \sum_{n=0}^{N'-1}\frac{B_{2n}\lr({\frac12})(s)_{2n-1}}{(2n)!}\lr({z+M-\frac12})^{-s-2n+1}}] \\ \Phi(-1,s,z) &= \lim_{M\to\infty} \lr[{\sum_{m=0}^{M-1}(-1)^m(z+m)^{-s} + \frac{(-1)^M}2\sum_{n=0}^{N'-1}\frac{E_{2n}\cdot(s)_{2n}}{4^n(2n)!}\lr({z+M-\frac12})^{-s-2n}}] \\ }$
となります。

厳密な証明には オイラー・マクローリンの和公式(Wikipedia) や オイラー・ブールの和公式(Wikipedia(英)) を使うものと思われます。

誤差

$\beginend{align}{ S(M) \acoloneqq \sum_{m=1}^M m^{-2} \\ T\lr({M,N'}) \acoloneqq \sum_{m=1}^M m^{-2} + \sum_{n=0}^{N'-1}B_{2n}\lr({\frac12})\lr({M+\frac12})^{-2n-1} \\ B_0\lr({\frac12}) &= 1, B_2\lr({\frac12}) = -\frac1{12} }$
$\beginend{alignat}{3 \zeta(2)-S(5) &= \frac{\pi^2}6-\lr({\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}}) &&= &&0.181322\cdots \\ \zeta(2)-T(5,1) &= \frac{\pi^2}6-\lr({\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}+ 5.5^{-1}}) &&= - &&0.000495\cdots \\ \zeta(2)-T(5,2) &= \frac{\pi^2}6-\lr({\frac11+\frac14+\frac19+\frac1{16}+\frac1{25}+ 5.5^{-1}-\frac{5.5^{-3}}{12}}) &&= - &&0.000005\cdots }$

系

式変形により別の級数の漸近級数展開を求めることもできます。

これは$\displaystyle \sahen = \int_{0\le s_1\le\cdots\le s_k} b^{-s_k}\Phi\lr({-1,s_k,\frac ab}) \prod_{l=1}^k ds_l$から導出します。
左辺の級数は収束が極めて遅いですが、右辺はかなり改善されます。
余りそちらの方面には詳しくありませんが、分数階積分により$k$が非整数でも成り立つと思われます。