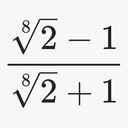2
大学数学基礎解説
素数の逆数和の発散を単純に
180
0
$$\newcommand{acoloneqq}[0]{\ &\hspace{-2pt}\coloneqq}
\newcommand{asupplement}[2]{&\hspace{#1}\text{#2}}
\newcommand{beginend}[2]{\begin{#1}#2\end{#1}}
\newcommand{C}[0]{\mathbb{C}}
\newcommand{hygeo}[6]{ {}_{#1}{#2}_{#3}\lr[{\beginend{matrix}{{#4}\\ {#5}}\ ;{#6}}]}
\newcommand{kfrac}[0]{\mathop{\matrix{\huge\rm K}}}
\newcommand{lr}[3]{\left#1{#2}\right#3}
\newcommand{N}[0]{\mathbb{N}}
\newcommand{P}[0]{\mathbb{P}}
\newcommand{Q}[0]{\mathbb{Q}}
\newcommand{R}[0]{\mathbb{R}}
\newcommand{range}[3]{\rangeex{}{#1}{}{#2}{#3}}
\newcommand{rangeex}[5]{#1{#2}_{#4}#3,\cdots,#1{#2}_{#5}#3}
\newcommand{sahen}[0]{(\text{左辺})}
\newcommand{stirling}[3]{\lr[{\beginend{matrix}{{#1}\\ {#2}}{#3}}]}
\newcommand{Stirling}[3]{\lr\{{\beginend{matrix}{{#1}\\ {#2}}{#3}}\}}
\newcommand{uhen}[0]{(\text{右辺})}
\newcommand{Z}[0]{\mathbb{Z}}
$$
この方法は前にどこかのサイトで見かけたものです。
$\beginend{align}{ n &\ge 1 \\ S_n \acoloneqq \sum_{k=1}^n \frac{1}{p_k} \\ T_n \acoloneqq \prod_{k=1}^n \lr({1+\frac{1}{p_k}}) }$
$\displaystyle T_n < \prod_{k=1}^n \lr({\frac1{0!}+\frac{1}{1!p_k}+\frac1{2!p_k^2}+\cdots}) = \prod_{k=1}^n e^{\frac1{p_k}} = e^{S_n}$
$\displaystyle \prod_p \lr({1+\frac1p}) =
\prod_p \frac{1-\frac1{p^2}}{1-\frac1p} =
\prod_p \frac{\frac11+\frac1p+\frac1{p^2}+\cdots}{\frac11+\frac1{p^2}+\frac1{p^4}+\cdots} =
\frac{\frac11+\frac12+\frac13+\cdots}{\frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\cdots} = \infty$
である為$T_n$は正の無限大に発散する。
よって$S_n$は正の無限大に発散する。
投稿日:2023年7月29日
更新日:2024年9月25日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中