ライツアウトのある解法の正当性の証明

　 前回 に続き、ライツアウトの記事です。

　 勉強中さんの記事 で、下記のブログ記事が紹介されていました。

• 人生ってそういうものなんだと思います

　こちらの記事でライツアウトの興味深い解法が紹介されていたものの、証明がついていなかったので、勝手に考えてみました。なお、katsubiさんの記事では$3 \times 3$から$10 \times 10$まで扱っていますが、ここでは$5 \times 5$と$3 \times 3$のみ扱うことにします。

準備

　以下、$5 \times 5$の場合で記述しますが、一般の場合でも同様です。
　前回の記事と同様、光っているマスを1, 光っていないマスを0とし、縦1列をベクトルと見なします。例えば

という盤面は

$$ \matea 01100, \matea 11011, \matea 00010, \matea 11010, \matea 10001$$

というベクトルの列と同一視されます。
　また、「ある列の光っているマスの右隣のマスをすべて押す」という操作をよく使います。例えば上の盤面で、左端の列に着目してこの操作を行うと、左から2列目の2,3番目のボタンを押して

となります。この操作により、左端の列のライトがすべて消えます。この操作を1,2列目で右寄せと呼ぶことにしましょう。ここからさらに2,3列目、3,4列目、$\cdots $ と続けて右寄せを行うと、最後には右端の列のみにライトが残った(もしくはライトがすべて消えた)状態になります。このように右端まで右寄せを行うことを、端まで右寄せと呼ぶことにします。

　右寄せを式で表します。前回の記事と同様、
$$ A = \matea{\rowe 11000}{\rowe 11100}{\rowe 01110}{\rowe 00111}{\rowe 00011}$$
とおきます。すると

と表せます。ここで、行列やベクトルの計算はすべて mod 2 で行います。

katsubiさんの解法($5 \times 5$)

　katsubiさんによる$5 \times 5$ライツアウトの解法を紹介し、その解法が正しいことを証明します。まず解法を述べます。ただし、ここでの話に合うように向きを回転させています。

(2)が少し気になるところですが、実に分かりやすい手順です。パターンや公式を暗記する必要がないのが嬉しいですね。

　では、この解法で本当に解けるということを確認していきます。端まで右寄せを行った後の状態をベクトルで表して
$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm c \end{matrix}$$
とします。ここからまず、どうにかして

$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm d & \mathbf 0 \end{matrix}$$

のような右から2列目のみが光っている状態にする必要があります。

　色々考えましたが、結局全部書き上げるのが手っ取り早そうなので書きます。まず前提として、与えられた盤面はクリア可能である必要があります。前回の記事の結果を使えば、
$$ \bm c = \matea{c_1}{c_2}{c_3}{c_4}{c_5}$$
とおいたとき、
$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm c \end{matrix}$$
がクリア可能であるための必要十分条件は
$$ c_1 +c_3 +c_5=0 \quad \text{ かつ } \quad c_2 + c_3 + c_4=0$$
が成り立つことでした。この条件を満たす盤面は実は8つしかなく、

で全てです。最初のものはすでに解けているので良いとして、残りの7つについて、右から2列目のみが光っている状態に変化させられることを確認します。
　実は、右端の列だけを見て「最下段までの下寄せ」を行えばOKです。

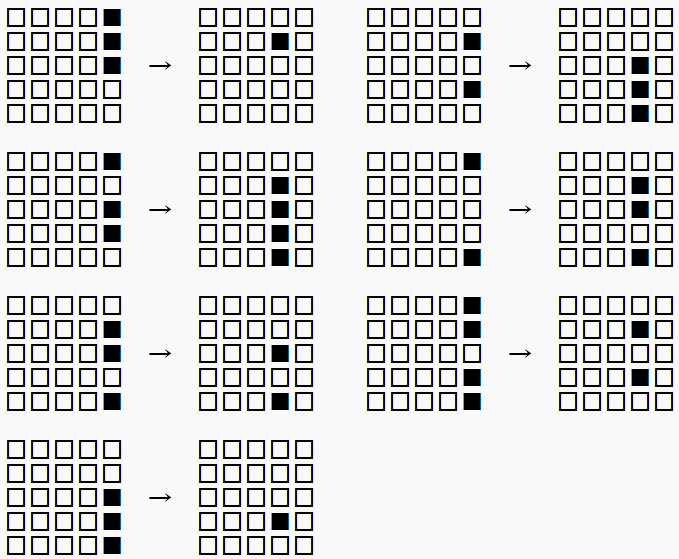
これで(2)の操作が可能であることが確かめられました。なお、これらの操作は一例であり、(2)の操作後に上記と異なる結果になる場合もあります。

　ちなみに他の方針として、「右端の列のみを$5 \times 1$のライツアウトと見なして解く」というのもありました。上のようにパターンを列挙することなく、前回と同様の考え方を用いて示すことができます。ただ、上の方針に比べて伝わりにくいかなと思ったので、上の方針を採用しました。

　さて、先の話に進むための準備として、「(2)の操作後、右から2列目はどのような光り方になっているか」を考えます。
$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm d & \mathbf 0 \end{matrix}$$
がクリア可能であるのは $\bm d$ がどのようなベクトルのときか、を考えれば良いですね。この状態から4,5列目で右寄せを行うと
$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & A \bm d \end{matrix}$$
となります。これがクリア可能であるためには、$A \bm d$の第2,3,4成分の和、第1,3,5成分の和が$0$であることが必要十分です。この条件は、行列を用いて
$$ \matba{\rowe 01110}{\rowe 10101} A \bm d = \matba 00$$
と表すことができます。ここで
$$ \matba{\rowe 01110}{\rowe 10101} A = \matba{\rowe 01110}{\rowe 10101} \matea{\rowe 11000}{\rowe 11100}{\rowe 01110}{\rowe 00111}{\rowe 00011} = \matba{\rowe 10101}{\rowe 10101}$$
なので、条件は$\matae 10101 \bm d = 0$と同値になります。

　それでは、(3),(4)の手順を検証しましょう。(3)では、
$$ \begin{matrix}   \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm d & \mathbf 0 \end{matrix}$$
という状態から、$\bm d$における$1$の位置と同じ段にある1列目のボタンを押します。これは
$$ \begin{matrix}   (\bm d) & \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm d & \mathbf 0 \end{matrix}$$
のように「0列目」に$\bm d$があると考え、0,1列目で右寄せを行うことと同じです。
$$ \begin{matrix}   (\bm d) & \mathbf 0 & \mathbf 0 & \mathbf 0 & \bm d & \mathbf 0\\   &&&\text{↓}&&\\    & A\bm d & \bm d & \mathbf 0 & \bm d & \mathbf 0 \end{matrix}$$
(4)では、ここからさらに端まで右寄せを行います。命題1の公式を繰り返し用いれば、
$$ \begin{matrix}    & A\bm d & \bm d & \mathbf 0 & \bm d & \mathbf 0\\   &&&\text{↓}&&\\    & \mathbf 0 & (A^2+E)\bm d & A\bm d & \bm d & \mathbf 0\\    &&&\text{↓}&&\\    & \mathbf 0 & \mathbf 0 & A^3\bm d & A^2\bm d & \mathbf 0\\    &&&\text{↓}&&\\    & \mathbf 0 & \mathbf 0 & \mathbf 0 & (A^4 + A^2)\bm d & A^3 \bm d\\    &&&\text{↓}&&\\    & \mathbf 0 & \mathbf 0 & \mathbf 0 & \mathbf 0 & A^5 \bm d \end{matrix}$$
となります。あとは$A^5\bm d = \mathbf 0$を示せばOKです。

　$A^5$は前回の記事で計算してあり、
$$ A^5 = \matea{\rowe 10101}{\rowe 00000}{\rowe 10101}{\rowe 00000}{\rowe 10101}$$
となります。ここで命題2より、$\bm d$は
$$ \matae 10101 \bm d = 0$$
を満たします。したがって、確かに$A^5\bm d = \mathbf 0$が成り立ちます!

　以上により、katsubiさんの解法で確かに$5 \times 5$ライツアウトが解けることが証明できました。案外大変でした。とりあえず右寄せを計算してけばサクッと示せるだろう、ぐらいに考えていたのですが、「クリア可能な盤面である」という仮定を元にちゃんと議論しなければならないというのが誤算でした。

katsubiさんの解法($3 \times 3$)

　続いて$3 \times 3$の場合です。まずは解法から。例によって、向きを回転させています。

$5 \times 5$の(2)のような曖昧さが無い分、考えやすいです。

　まず、前回の記事で確かめたように、$3 \times 3$ライツアウトはいつでもクリア可能です。なので、先ほどのようにクリア可能かどうかを気にする必要はありません。
　(1)で端まで右寄せを行った後の状態を
$$ \begin{matrix} \mathbf 0 & \mathbf 0 & \bm c \end{matrix}$$
としましょう。(2)の操作は、
$$ \begin{matrix} \mathbf 0 & \mathbf 0 & \bm c & (\bm c) \end{matrix}$$
のように4列目に$\bm c$があると見なし、3,4列目で「左寄せ」を行うことと思うことができます。すると
$$ \begin{matrix} \mathbf 0 & \mathbf 0 & \bm c & (\bm c)\\ &&\text{↓} \qquad &\\ \mathbf 0 & \bm c & (A+E)\bm c & \end{matrix}$$
となります。次に段ごとに光っているマスが奇数個かどうかをカウントしますが、これは$\bm c + (A+E)\bm c$を計算することにほかなりません。計算すると
$$ \bm c + (A+E)\bm c = A\bm c$$
となりますね。これに合わせて左端の列のボタンを押すので、
$$ \begin{matrix} (A\bm c) & \mathbf 0 & \bm c & (A+E)\bm c \end{matrix}$$
と0列目に$A\bm c$があると仮定し、0,1列目で右寄せを行えば良いです。その次の「端まで右寄せ」もまとめて計算すると、
$$ \begin{matrix} (A\bm c) & \mathbf 0 & \bm c & (A+E)\bm c \\ &&\text{↓}&\\ & A^2\bm c & (A+E)\bm c & (A+E)\bm c\\ &&\text{↓}&\\ & \mathbf 0 & (A^3 + A+E)\bm c & (A^2 + A+E)\bm c\\ &&\text{↓}&\\ & \mathbf 0 & \mathbf 0 & (A^4 + E)\bm c \end{matrix}$$
となります。あとは$(A^4+E)\bm c = \mathbf 0$を確かめれば証明完了です。
　$A = \matcc 110111011$の4乗を計算すると
$$ A^4 = \matcc 100010001 = E$$
となることが分かります。したがって$A^4+E=O$なので、
$$ (A^4+E)\bm c = \mathbf 0$$
が成り立ちます！

　以上により、$3 \times 3$の場合もkatsubiさんの解法が正しいことが示されました。こちらは機械的な計算で済みましたね。「いつでも解ける」というのが効いているのだと思います。

おわりに

　今回は、katsubiさんによる$5 \times 5$ライツアウトと$3 \times 3$ライツアウトの解法が正しいことを証明しました。katsubiさんは他にも$6 \times 6$から$10 \times 10$までの解法を開発していますが、頑張れば今回と同じように証明できるのではないかと思います。ちなみに、前回から用いている「1つの列を一かたまりと見なす」という見方を思いついたのは、katsubiさんの$5 \times 5$の解法をうまく証明できないかと考えたのがきっかけです。今回で当初の目的を達成することができました。
　証明こそできましたが、今回の証明からは「どうやったら思いつけるのか」は全く見えてこないですね。katsubiさんは特に数学は使わず、観察や試行錯誤によってこれらの解法を編み出したというのですから驚きです。人間の可能性のようなものを感じます。
　ライツアウトについてはもうちょっと何か書くかもしれません。

　ではまた