求角問題と外心３つ法と「外心10個法」（前編）

　匿です。今回も研究成果を掲載していきます。

Too Abstract Abstract

　これが

こうなります。

Long Introduction

　初等幾何の歴史の中で、求角問題というジャンルは長きにわたり注目されてきました。「与えられた問題図における何らかの角度の大きさを尋ねる問題」であればいずれも求角問題と呼べてしまうのですが、1922年にEdward Mann Langley氏が発表した求角問題（所謂『 ラングレーの問題 (Langley's Adventitious Angles)』）は、その特徴的な問題設定から「整角四角形」というグループを築くに至りました。

　例えば、$\angle ABD={38}^{\circ},$$\angle CBD={46}^{\circ},$$\angle ACB={22}^{\circ},$$\angle ACD={48}^{\circ}$である四角形$ABCD$を作図してみると、$\angle ADB={18}^{\circ}$となります。したがって、このとき四角形$ABCD$は整角四角形である、といえます（下図）。また、「$\angle ABD={38}^{\circ},$$\angle CBD={46}^{\circ},$$\angle ACB={22}^{\circ},$$\angle ACD={48}^{\circ}$の四角形$ABCD$において、$\angle ADB$の大きさを求めなさい」と書けば、整角四角形問題がひとつ完成しますね。

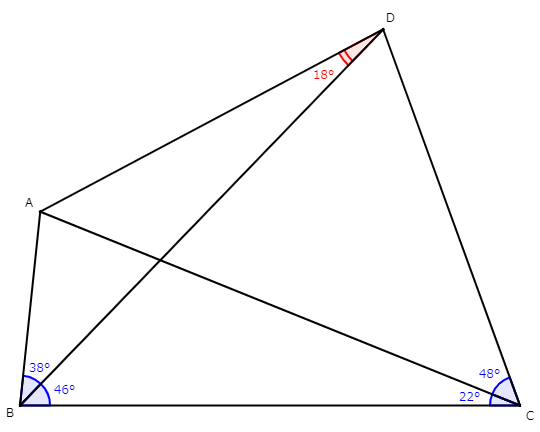
　次に、$2$以上の整数$n$について、$n$等辺$(n+1)$角形を定義します。

　二等辺三角形は一般によく浸透していますが、それを拡張したような定義ですね。便宜上、$n$等辺$(n+1)$角形については$n$および$n+1$を漢数字で表記します。当然ながら、正$(n+1)$角形も$n$等辺$(n+1)$角形に含まれます。
　$n$等辺$(n+1)$角形問題について、以下の強力な定理が知られています。

　定理1の証明には多項式環などの知識が必要とな（り筆者の数学力では到底手に負えなくな）るため、ここでは証明を割愛します。

　さて、四角形$ABCD$が円に内接するならば、明らかに整角四角形の定義をみたします。円に内接しない場合、 こちらの整角四角形問題生成サイト によると、整角四角形を構成する$(\angle ABD,$$\angle CBD,$$\angle ACB,$$\angle ACD)$の組は62,804通り考えられるそうです。1日10問ずつ解いても17年以上、凄まじい量ですね。
　この62,804通りすべてに有効な幾何解法は存在するのでしょうか。結論から申し上げると、イエスです。2015年10月、あれれ（aerile_re）氏という方が画期的なメソッドを発見し、任意の整角四角形を六等辺七角形に帰着させてしまいました。このメソッドは「外心３つ法（3 circumcenter method）」と名付けられ、発見後わずか数か月で世界中の初等幾何愛好者を感嘆させました。
　有難いことに 開発者ご本人による解説記事 や 斉藤浩氏による論文化 もあり、興味のある方はそれらの文献で本格的に学ぶのが望ましいです（高校１～２年生の頃に私も勉強させていただきました）。本記事は外心３つ法の先の世界をメインとしたいため、外心３つ法自体についてはそのイメージを軽く掴んでいただく程度の記述にとどめます。

　はい、聞こえていましたか？
　そうです。外心３つ法の先の世界が、本記事のメインテーマです。外心３つ法と同様のアプローチで、以下の「二段整角四角形問題」に挑みます。

　難解な書き方をしていますが、要するにこういう形の問題です。青い角の大きさが与えられたときに、赤い角の大きさを求めます（以下の例では$\angle ADE={13}^{\circ}$になります）。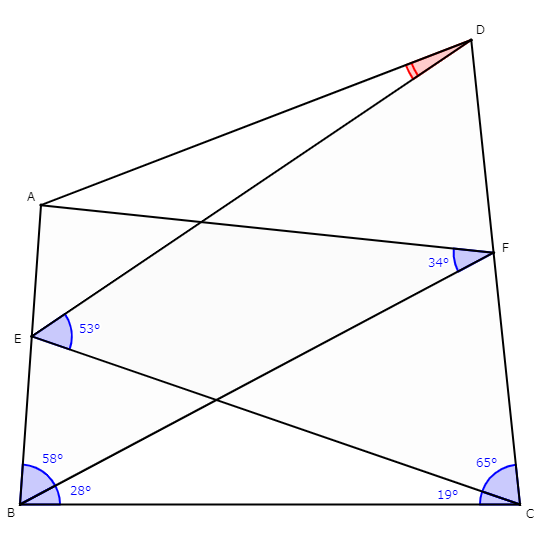

　整角四角形が2つ積み重なったような構造です。言うまでもなく、難易度は飛躍的に上がります（上の例はそこまで難しくありませんが……）。普通の整角四角形でさえ難しそうなメソッドを求められた手前、いっそ途方に暮れたくなりますね。
　私は宣言通り外心３つ法を応用し、二段整角四角形問題を完全に解決しました。すべての二段整角四角形問題もまた初等幾何で解けるのです。良いですね。この応用によって生まれたメソッド、いわば「外心10個法」を具体的に紹介するのが、本記事の最終目標です。

"3 Circumcenter Method"

　先程掲載した$\angle ABD={38}^{\circ},$$\angle CBD={46}^{\circ},$$\angle ACB={22}^{\circ},$$\angle ACD={48}^{\circ}$の例で、外心３つ法の流れを見てみましょう（先述の2つの文献にもほぼ同様の解説が載っています）。
　このメソッドは、まず外心を3回作図するところから始まります。$\triangle ABC$の外心を$O_1$、$\triangle DBC$の外心を$O_2$とし、さらに$\triangle O_1 O_2 C$の外心を$O_3$としましょう。

　任意の整角四角形において、直線$BC$を基準とした偏角を考えれば、$AB,AC,$$DB,DC$の偏角はいずれも度数法で整数値をとります。ゆえに、外心の性質から$AO_1,BO_1,CO_1,$$DO_2,BO_2,CO_2,$$O_1 O_3, O_2 O_3, CO_3$の偏角もまた整数値ですね（実はこれが外心３つ法の要になります）。
　いま$AO_1=CO_1$ですから、$\triangle CO_3 O_1 \equiv \triangle A P_1 O_1$となる点$P_1$をとることができます。同様に、$\triangle CO_3 O_2 \equiv \triangle D P_5 O_2$となる点$P_5$をとることもできます。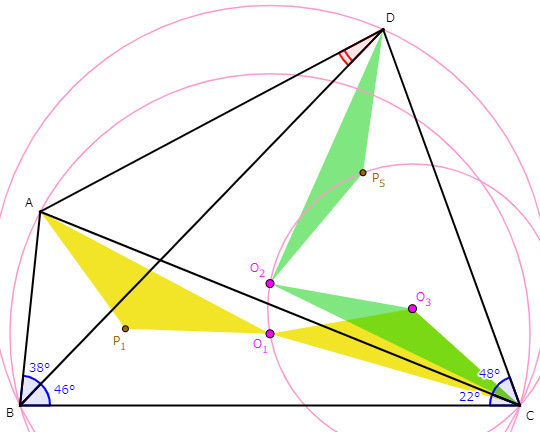

　$A=P_0,$$O_1=P_2,$$O_3=P_3,$$O_4=P_4,$$D=P_6$と別名を付け、折れ線$P_0 P_1 P_2 P_3 P_4 P_5 P_6$に注目します。外心の性質から、この折れ線の各線分はすべて同じ長さになっており、かつ偏角は整数値です。したがって、もとの整角四角形問題が七角形$P_0 P_1 P_2 P_3 P_4 P_5 P_6$に関する六等辺七角形問題に変換されたのです。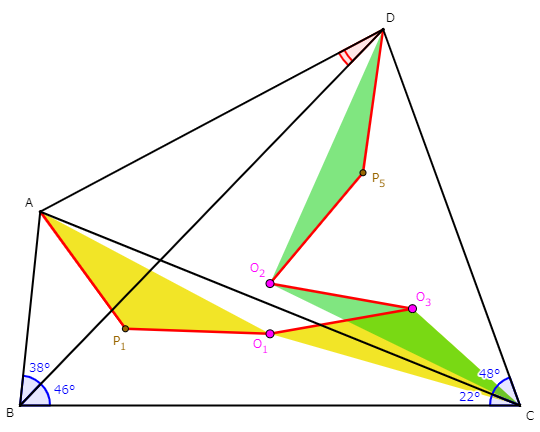

　あとはどうとでもなります。定理1から初等的な可解性が保証されており、ただ有限回の試行錯誤をするだけです。今回の問題であれば、以下の図のように正三角形や正五角形をとることで、忽ちに直線$P_0 P_6$の偏角が${28}^{\circ}$であると導かれます（計算略）。これは$\angle ADB={18}^{\circ}$と同値です。完答。おめでとうございます。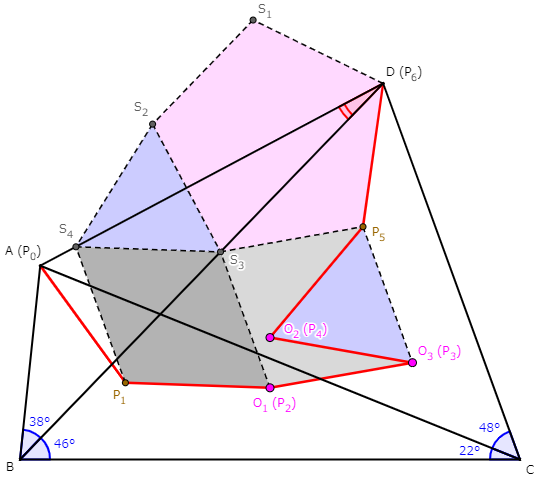

"10 Circumcenter Method"

　外心３つ法の凄さが分かったところで、いよいよ二段整角四角形の話題に移ります。復習ですが、以下の図のような問題を本記事では二段整角四角形問題と呼んでいます（灰色の角度が与えられたときに桃色の角度を求める）。四角形$EBCF,$$AECF,$$DEBF$が整角四角形であればただの整角四角形問題になってしまうので、以下ではこれらが整角四角形でない場合のみを考えます。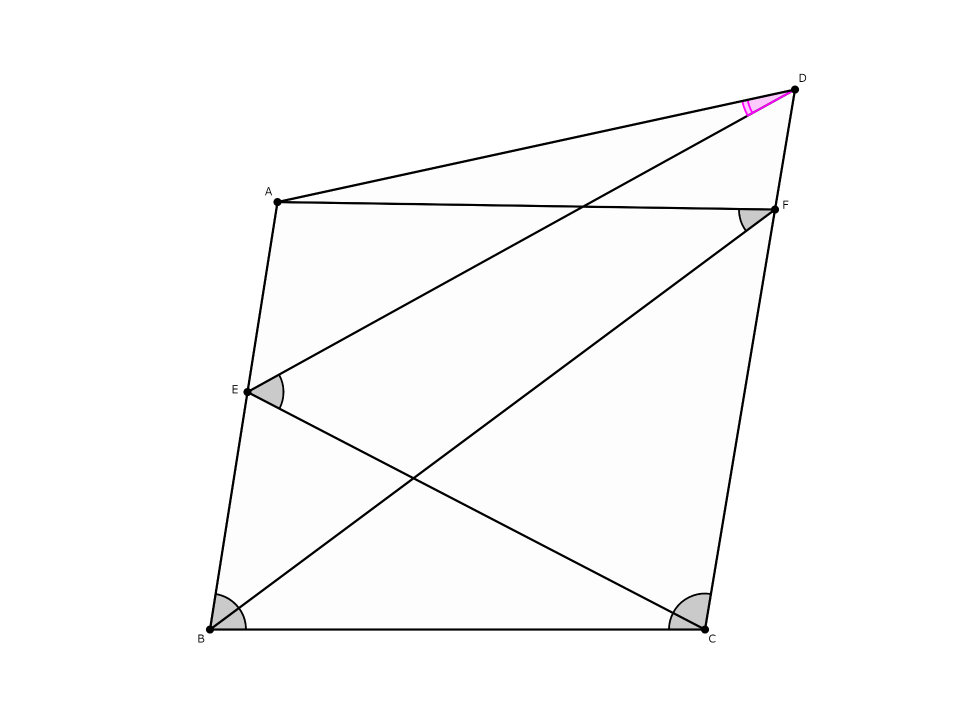

　今回作図する外心は10個です。$\triangle EBC, \triangle FBC$の外心を$O_1, O_2$、$\triangle O_1 O_2 B, \triangle O_1 O_2 C$の外心を$O_3, O_4$、$\triangle ABF, \triangle DCE$の外心を$O_5, O_6$、$\triangle O_2 O_5 B, \triangle O_1 O_6 C$の外心を$O_7, O_8$、$\triangle O_2 O_3 O_7, \triangle O_1 O_4 O_8$の外心を$O_9, O_{10}$とします。既に厳しいですね。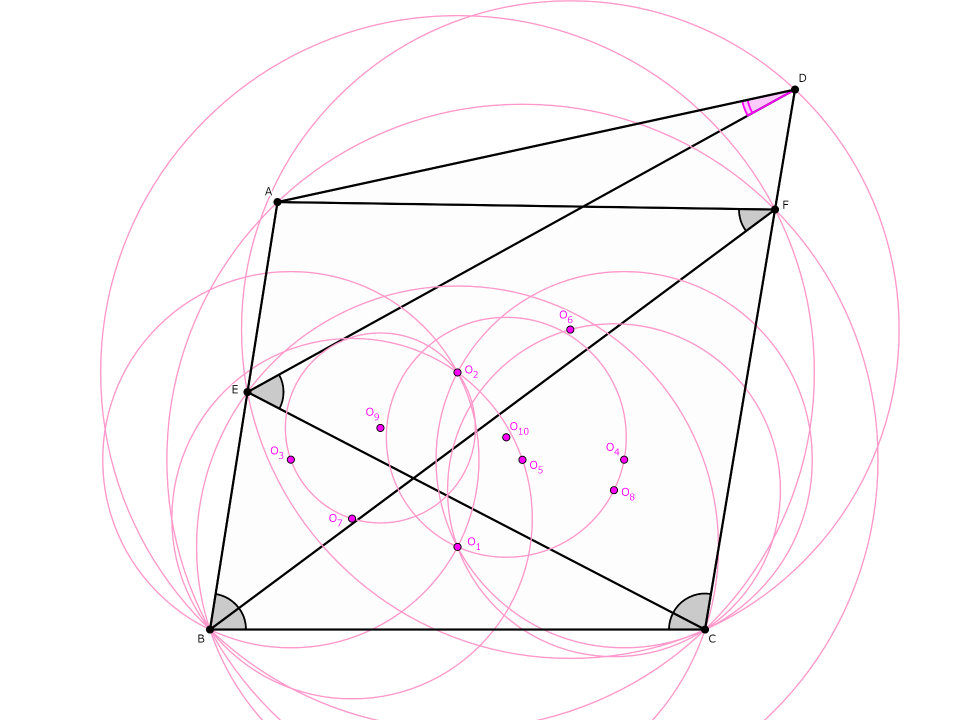

　相変わらず直線$BC$を基準とします。$O_1$～$O_3$は四角形$EBCF$に対し外心３つ法を施したときと同じとり方ですから、$EO_1,BO_1,CO_1,$$FO_2,BO_2,CO_2,$$O_1 O_3,O_2 O_3,BO_3$の偏角は整数値です。同様に$O_1 O_4,O_2 O_4,CO_4$の偏角も整数値ですね。また、$\triangle ABF,\triangle DCE$の各辺の偏角が整数値のため、$AO_5,BO_5,FO_5,$$DO_6,CO_6,EO_6$の偏角も整数値となります。直線$O_2 O_5,O_1 O_6$はそれぞれ線分$BF,CE$の垂直二等分線ですから、それらの偏角は整数値と判ります。よって$\triangle O_2 O_5 B, \triangle O_1 O_6 C$の各辺の偏角が整数値、すなわち$O_2 O_7, O_5 O_7, BO_7,$$O_1 O_8, O_6 O_8, CO_8$の偏角も整数値です。これまでと同様の考察から、$O_2 O_9, O_3 O_9, O_7 O_9,$$O_1 O_{10}, O_4 O_{10}, O_8 O_{10}$の偏角も整数値といえます。まとめると、外心をとった10個の三角形は、いずれも各頂点から外心までの偏角が整数値になっています。ちなみにこのパラグラフにおける「偏角」・「整数値」の登場回数は計20回でした（鍵括弧の中も含む）。

　$\angle O_2 O_9 O_7=2\angle O_2 O_3 O_7$$=\angle O_2 O_3 B$$={360}^{\circ}-2\angle O_2 O_1 B$$=\angle B O_1 C$より、$\triangle BO_1 C$と$\triangle O_2 O_9 O_7$は相似です。同様に、$\triangle BO_2 C$と$\triangle O_1 O_{10} O_8$も相似と判ります。このことを踏まえ、$\triangle CO_8 O_1 \sim \triangle O_2 XO_9$をみたす点$X$および$\triangle BO_7 O_2 \sim \triangle O_1 YO_{10}$をみたす点$Y$をとってみましょう。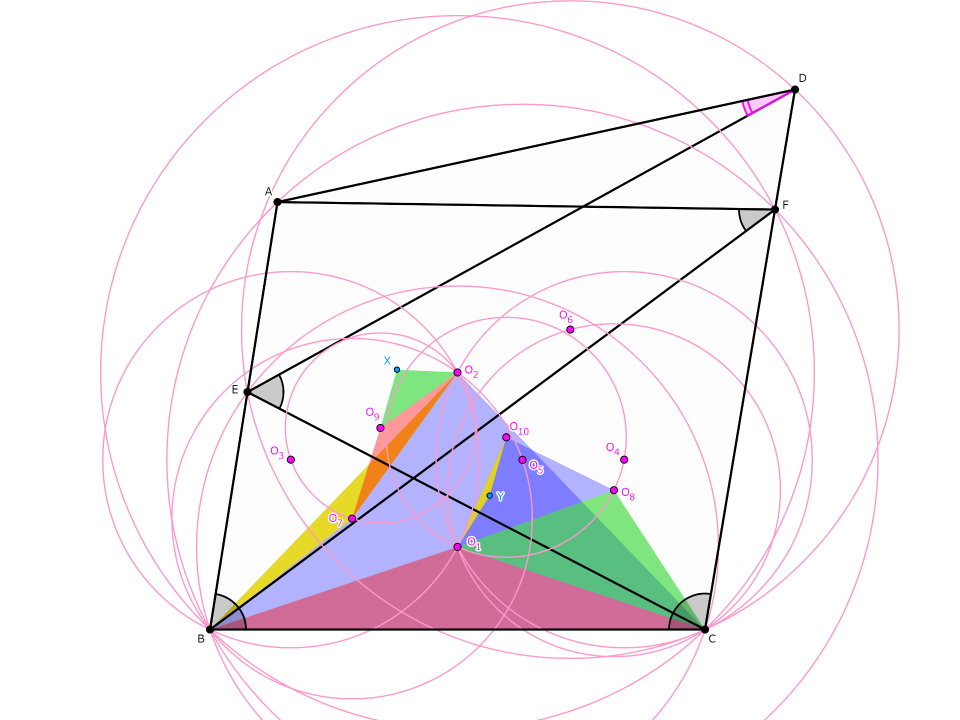

　実は$XO_2=YO_1$が成り立つのですが、確かめられますか？
　簡単ですね。相似関係に注目し以下のような比の計算をすれば、すぐに証明できます。
$$\begin{aligned} \dfrac{XO_2}{BC} &=\dfrac{XO_2}{O_2 O_9}\times\dfrac{O_2 O_9}{O_2 O_7}\times\dfrac{O_2 O_7}{BO_2}\times\dfrac{BO_2}{BC} \\ &=\dfrac{O_1 O_8}{CO_1}\times\dfrac{CO_1}{BC}\times\dfrac{YO_1}{O_1 O_{10}}\times\dfrac{O_1 O_{10}}{O_1 O_8}=\dfrac{YO_1}{BC} \end{aligned}$$
　さあ、これで準備は整いました。外心３つ法と同じように、長さが等しくなる辺へ$\triangle O_2 XO_9$と$\triangle O_1 YO_{10}$を順次貼りつけていきましょうか。実際に貼りつけた一例を以下に示します（緑色と黄色の小三角形はいずれもそれぞれ合同です）。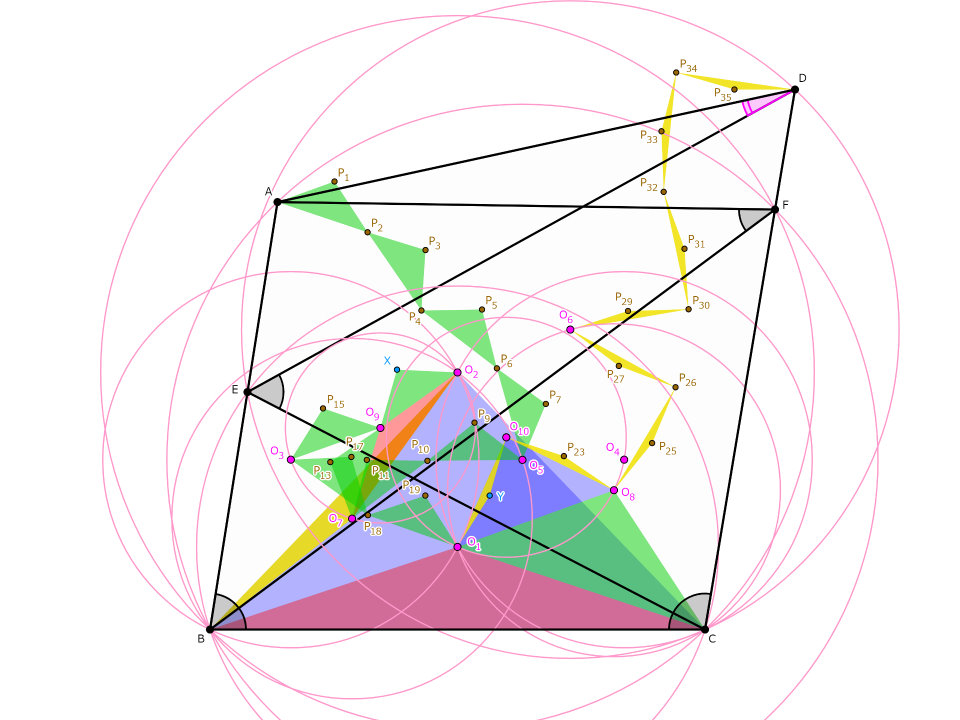

　$O_2 O_9=O_3 O_9=O_7 O_9$から$P_{13},P_{15}$を作図できて、$O_2 O_7=O_5 O_7$から$P_{9}$～$P_{11}$を、$O_2 O_3=O_1 O_3$から$P_{17}$～$P_{19}$をそれぞれとれます。$\triangle BO_7 O_5 \equiv \triangle AP_4 O_5$をみたす点$P_4$をとれば、$AP_4=O_5 P_4=O_5 O_7$を用いて$P_1$～$P_3$および$P_5$～$P_7$が描かれます。同様にして$P_{23}$、$P_{25}$～$P_{27}$、$P_{29}$～$P_{35}$も拵えます。


　$A=P_0,$$O_5=P_8,$$O_7=P_{12},$$O_9=P_{14},$$O_3=P_{16},$$O_1=P_{20},$$Y=P_{21},$$O_{10}=P_{22},$$O_8=P_{24},$$O_6=P_{28},$$D=P_{36}$と別名を付けることで、折れ線$P_0 P_1 P_2 \dots P_{36}$を考えられます（下図の赤線）。この折れ線の各線分はすべて同じ長さになっており、かつ偏角は整数値です。したがって、もとの二段整角四角形問題が三十七角形$P_0 P_1 P_2 \dots P_{36}$に対する三十六等辺三十七角形問題に帰着されたのです。これにてすべての二段整角四角形問題に初等幾何解法が与えられることは、相変わらず定理1のお陰で保証されます。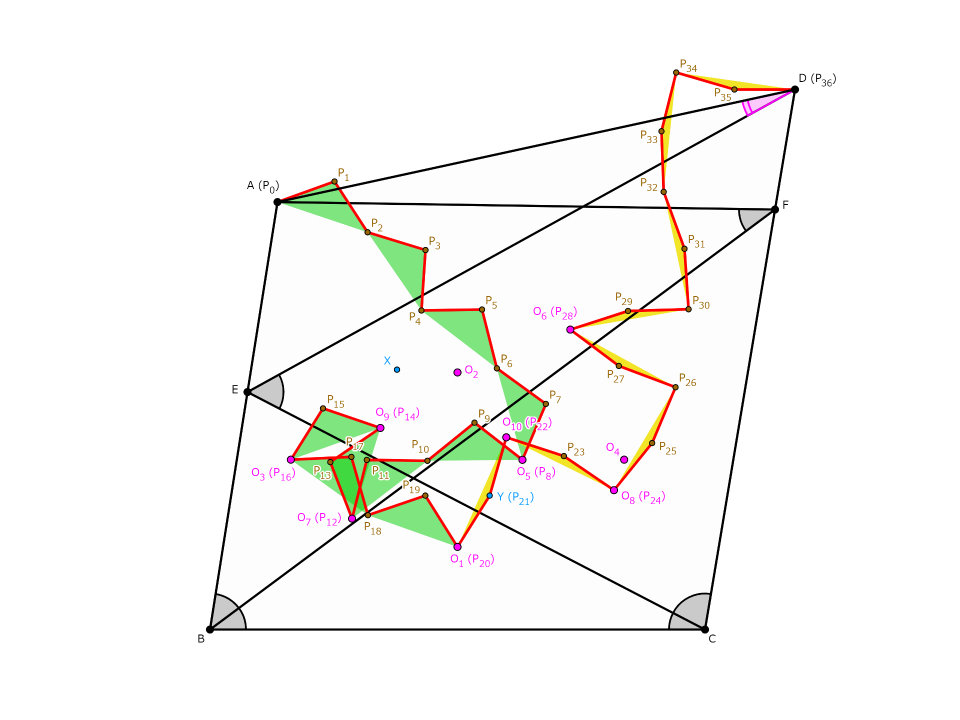

　以上が、私の提案する「外心10個法」の全容です。

To The Next Article

　案の定長くなってきたため記事を二分割し、こちらの記事を前編として扱うことにします。後編ではたった今紹介した外心10個法を利用し、実際に二段整角四角形問題を解いてみせます。ご期待ください。
　ところで、変換後の三十六等辺三十七角形を見て
「勝った、この程度ならば一瞬で解ける」
と脳内でエンディングテーマを流してしまうのは、私の感性がダメになった証拠でしょうか。数か月前までは六等辺七角形さえも怖れていたのですが……。

　感想・提案・質問・指摘・先行研究報告などはコメントにお願いします。

<2024/07/21追記>

　本記事の 後編 を投稿しました。執筆しておいてどうかとは思いますが、徹頭徹尾観賞用です。それでも良い方はお読みくださいませ（「後編」の文字がハイパーリンクになっています）。