文献あり

求角問題と外心３つ法と「外心10個法」（後編）

694

　ウェブサイト軽量化のため、一部画像の解像度を落としています。点線で囲まれた画像をクリックすると、その画像の高解像度版が新しいタブで表示されます。

　前編をお読みくださった皆様、こんにちは。本記事では、前編で紹介した「外心10個法」を活用し、（おそらく）非常に難しい求角問題を初等幾何で解決してみます。

A Problematic Problem

　凸四角形 $A B C D$ の辺 $A B, C D$ 上にそれぞれ点 $E, F$ をとると、 $∠ A B F = 58^{\circ},$ $∠ C B F = 28^{\circ},$ $∠ E C B = 38^{\circ},$ $∠ E C D = 46^{\circ},$ $∠ A F B = 78^{\circ},$ $∠ D E C = 72^{\circ}$ が成立した。このとき $∠ A D E$ の大きさは度数法で整数値となるが、その値を求めなさい。

　前回定義した二段整角四角形問題そのものです。余程のこだわりがない限りは三角関数を利用しゴリゴリと計算するのがよいですけれども、ここは敢えて余程のこだわりを見せます。以前共同研究した某氏も「人々にとって初等幾何とエンジョイは同値」と仰っており、初等幾何解法の発見はきっと皆様のエンジョイにコミットできます。……できますよね？

Is the Elementary Solution Elementary?

折れ線10分クッキング

　外心10個法の初手は10個の外心をとることです。 $△ E B C, △ F B C$ の外心を $O_{1}, O_{2}$ 、 $△ O_{1} O_{2} B, △ O_{1} O_{2} C$ の外心を $O_{3}, O_{4}$ 、 $△ A B F, △ D C E$ の外心を $O_{5}, O_{6}$ 、 $△ O_{2} O_{5} B, △ O_{1} O_{6} C$ の外心を $O_{7}, O_{8}$ 、 $△ O_{2} O_{3} O_{7}, △ O_{1} O_{4} O_{8}$ の外心を $O_{9}, O_{10}$ とします。 $△ B O_{1} C \sim △ O_{2} O_{9} O_{7}$ および $△ B O_{2} C \sim △ O_{1} O_{10} O_{8}$ が成立していたので、 $△ C O_{8} O_{1} \sim △ O_{2} X O_{9}$ をみたす点 $X$ および $△ B O_{7} O_{2} \sim △ O_{1} Y O_{10}$ をみたす点 $Y$ をとれば、 $X O_{2} = Y O_{1}$ を導出できます（前編のこの部分を参照）。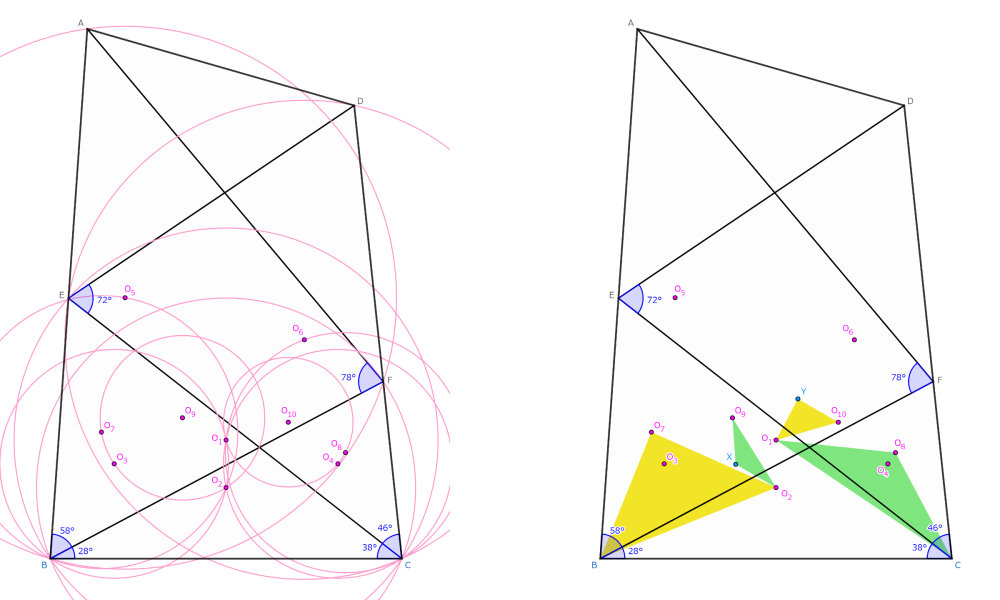

　外心がつくる等長関係に注目し、 $△ O_{2} X O_{9}, △ O_{1} Y O_{10}$ と合同な三角形をペタペタペタペタペタペタペタペタペタペタペタペタペタペタペタペタペタと貼り付けます。すると下図のように $P_{0}$ ～ $P_{36}$ が定められ、本問は三十七角形 $P_{0} P_{1} P_{2} \dots P_{36}$ に対する三十六等辺三十七角形問題に帰着されます。なお、 $P_{0}$ ～ $P_{36}$ のとり方は $2^{26}$ 通り存在し、下図はそのうちの一例に過ぎません。
　ここまでが下準備、外科手術でいうところの麻酔導入です。~~下準備で補助線57本と補助円10個？~~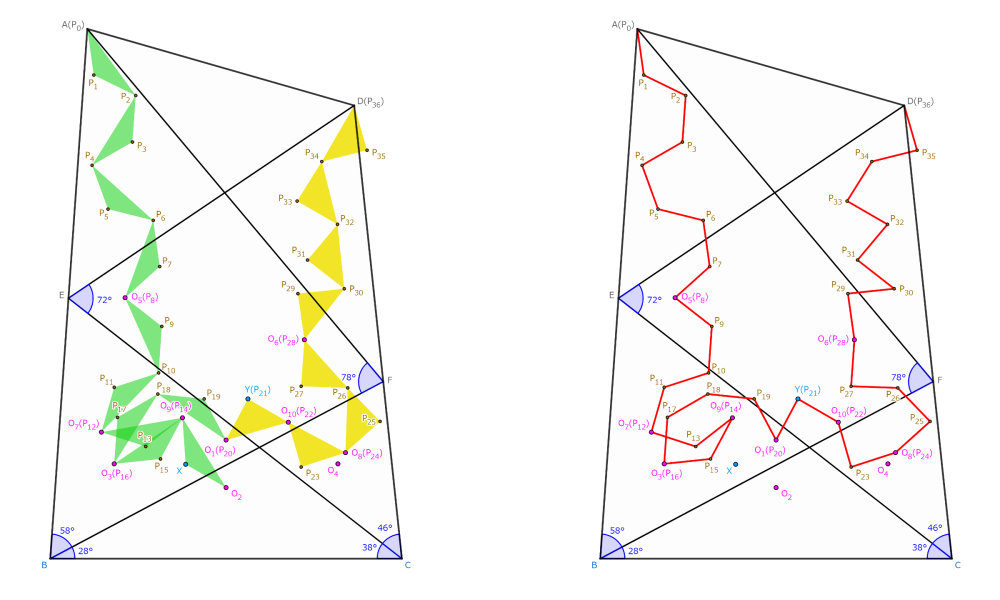

　これまで呼吸のごとく「線分○○の偏角」と言ってきましたが、調べてみたところ偏角は複素数に対して定義されるものであり、線分や直線は普通に角度で表記する例が殆どでした。とはいえ、一々「線分○○と線分△△のなす角」と書くのも可読性を欠き、何よりも外心3つ法の発案者が「折れ線の偏角」という語を用いていることから、これ以降は明確な理由をもって「線分○○の偏角」と連呼することにします。厳密性重視派の方へ先に謝っておきます、申し訳ございません。

　いま、上図右において、線分 $P_{n - 1} P_{n}$ の偏角を ${a_{n}}^{\circ}$ とすると、
$\begin{aligned} {a_{n}} = & 278, 334, 266, 210, 290, 346, 278, 222, 322, 266, 198, 254, \\ 342, 38, 242, 186, 86, 30, 354, 298, 62, 330, 286, 18, \\ 42, 134, 178, 86, 98, 6, 142, 50, 150, 58, 14, 106 \end{aligned}$
が確認されます（画面幅の狭いデバイスで閲覧される方に配慮し適宜改行を挟みました）。サラッと書きましたが、この確認を手計算で行おうとすると20分は必要です。
　簡単のため、勝手に $| P_{0} P_{1} | = 1$ と仮定しましょう。角度は不変です。以下、 $z$ は $\arg z = 1^{\circ}$ をみたす $1$ の360乗根、すなわち $z = \exp (\frac{π i}{180})$ とします。このとき、 $| ζ | = 1,$ $\arg ζ = m^{\circ}$ をみたす数 $ζ$ は $ζ = z^{m}$ と表現できるため、線分 $P_{0} P_{36}$ の偏角は $\arg (\sum_{k = 1}^{36} z^{a_{k}})$ に等しいです。可読性のために以下の関数 $Z$ を定義すると、この式は $\arg Z ({a_{n}})$ と書けます。

　 $N$ 項からなる有限数列 ${F_{n}}$ において、 $Z_{x, y} ({F_{n}}),$ $Z ({F_{n}})$ を
$\begin{array}{r} Z_{x, y} ({F_{n}}) = \sum_{k = x}^{y} z^{F_{k}}, Z ({F_{n}}) = \sum_{k = 1}^{N} z^{F_{k}} \end{array}$
と定める（ただし $z = \exp (\frac{π i}{180})$ ）。

　凄まじい観察眼を用いてエスパーする or 事前に三角関数などで計算しておくと、 $\arg Z ({a_{n}}) = {- 16}^{\circ}$ です。このことは $z^{16} Z ({a_{n}}) = Z ({a_{n} + 16})$ が実数であることと同値になるので、今からこれを代数的に確認します。

裏計算のお時間（読み飛ばし推奨）

　数列 ${{a^{(0)}}_{n}}$ を ${a^{(0)}}_{n} = (a_{n} + 16) % 360$ で定義すると（ $%$ は剰余演算子）、
$\begin{aligned} {{a^{(0)}}_{n}} = & 294, 350, 282, 226, 306, 2, 294, 238, 338, 282, 214, 270, \\ 358, 54, 258, 202, 102, 46, 10, 314, 78, 346, 302, 34, \\ 58, 150, 194, 102, 114, 22, 158, 66, 166, 74, 30, 122 \end{aligned}$
です。 $z^{360} = 1$ ですから、 $Z ({a_{n} + 16})$ が実数 $⟺$ $Z ({{a^{(0)}}_{n}})$ が実数、といえます。
　ここで、以下のような関数 $M$ を考えます。

　有限数列 ${F_{n}}$ において、 $M_{x, y} ({F_{n}})$ を
$M_{x, y} ({F_{n}}) = ({F_{n}} の第 x 項から第 y 項までを逆順にした数列)$
と定める。例えば、 ${F_{n}} = 1, 2, 3$ のとき $M_{1, 2} ({F_{n}})$ $= 2, 1, 3$ である。

　関数 $M$ の果たす役割を説明します。いま、 $z^{250} + z^{70}$ はガウス平面上で原点対称な数の和ですから $0$ と等しくなります。 $z^{20} + z^{140} + z^{260}$ はガウス平面上で原点を中心とする正三角形の頂点の和であり、こちらも $0$ です。ゆえに、
${Λ_{n}} = 250, 70, 20, 140, 260$
という数列を考えれば、自明に $Z ({Λ_{n}}) = 0$ です。
　それでは、こちらの数列 ${{Λ^{'}}_{n}}$ における $Z ({{Λ^{'}}_{n}})$ の値はいくらでしょうか。
${{Λ^{'}}_{n}} = 20, 70, 140, 250, 260$
　問うまでもありませんね。数列を構成する項がすべて対応するので、 $Z ({{Λ^{'}}_{n}})$ $= Z ({Λ_{n}})$ $= 0$ です。これは「 $M_{1, 3} (M_{3, 4} ({{Λ^{'}}_{n}}))$ と ${Λ_{n}}$ とが一致するため、 $Z ({{Λ^{'}}_{n}})$ $= Z ({Λ_{n}})$ $= 0$ 」とも言い換えられます。
　有限数列に関する計算を行う際、このように関数 $M$ を利用することで、視覚的に最も計算しやすい形へと数列が整理されます。それこそが関数 $M$ の役割です。……「わざわざ順番を入れ替えなくても計算可能ではないか？」と思われたかもしれません。もっともなご意見ですが、数列の項数が10項、20項と増えていけば、いずれ我々の脳のキャパシティを超えた複雑さを抱くでしょう。その際にも、互いに打ち消しあう項の組を関数 $M$ でまとめることで、計算が幾分か楽になります。加えて、数列の計算を初等幾何に還元する際、関数 $M$ はある操作に対応するのです（後述）。初等幾何解法を創出するうえでキーとなるのが、この関数 $M$ です。

　本題に戻ります。
$\begin{aligned} {{a^{(1)}}_{n}} & = M_{31, 35} (M_{28, 30} (M_{24, 27} (M_{19, 20} (M_{20, 21} (M_{12, 17} (M_{3, 6} ({{a^{(0)}}_{n}}))))))) \\ {{b^{(1)}}_{n}} & = M_{34, 36} (M_{20, 22} (M_{18, 19} (M_{17, 18} (M_{10, 11} (M_{7, 8} (M_{5, 9} ({{a^{(1)}}_{n}})))))))) \end{aligned}$
と定義すれば、
$\begin{aligned} {{a^{(1)}}_{n}} = & 294, 350, 2, 306, 226, 282, 294, 238, 338, 282, 214, 102, \\ 202, 258, 54, 358, 270, 46, 78, 10, 314, 346, 302, 194, \\ 150, 58, 34, 22, 114, 102, 30, 74, 166, 66, 158, 122 \\ {{b^{(1)}}_{n}} = & 294, 350, 2, 306, 338, 238, 282, 294, 226, 214, 282, 102, \\ 202, 258, 54, 358, 46, 78, 270, 346, 314, 10, 302, 194, \\ 150, 58, 34, 22, 114, 102, 30, 74, 166, 122, 158, 66 \end{aligned}$ であり、特に $Z_{11, 12} ({{b^{(1)}}_{n}})$ $= z^{282} + z^{102}$ $= 0$ です。ゆえに、 ${a^{(2)}}_{n} = {\begin{aligned} {b^{(1)}}_{n} (1 \leq n \leq 10) \\ {b^{(1)}}_{n + 2} (11 \leq n \leq 34) \end{aligned}$ とおくと $Z ({{a^{(2)}}_{n}}) = Z ({{b^{(1)}}_{n}})$ $(= Z ({{a^{(1)}}_{n}})$ $= Z ({{a^{(0)}}_{n}}))$ が成立します。

　次の操作を行う前に、数列 ${μ_{n}} = 30, 74$ と数列 ${{μ^{'}}_{n}}$ $= 14, 330,$ $134, 90$ を用意し、 $Z ({μ_{n}}) = Z ({{μ^{'}}_{n}})$ を示しておきます。左辺に $z^{180} (= - 1)$ を掛け右辺に移項すると、以下の等式を示せばよいことになります。
$z^{14} + z^{330} + z^{134} + z^{90} + z^{254} + z^{210} = 0$
　左辺を $z^{90} + z^{14}$ で括れば $(z^{90} + z^{14})$ $(z^{240} + z^{120} + z^{0})$ であり、 $z^{240} + z^{120} + z^{0}$ $= 0$ なので証明完了です。
　 ${{b^{(2)}}_{n}}$ $= M_{20, 23} (M_{7, 14} (M_{3, 6} ({{a^{(2)}}_{n}})))$ とすれば、
$\begin{aligned} {{b^{(2)}}_{n}} = & 294, 350, 238, 338, 306, 2, 358, 54, 258, 202, \\ 214, 226, 294, 282, 46, 78, 270, 346, 314, 150, 194, 302, \\ 10, 58, 34, 22, 114, 102, 30, 74, 166, 122, 158, 66 \end{aligned}$
ですね。 $Z_{29, 30} ({{b^{(2)}}_{n}})$ $= z^{μ_{1}} + z^{μ_{2}}$ $= Z ({μ_{n}})$ なので、 ${a^{(3)}}_{n} = {\begin{aligned} {b^{(2)}}_{n} (1 \leq n \leq 28) \\ {μ^{'}}_{n - 28} (29 \leq n \leq 32) \\ {b^{(2)}}_{n - 2} (33 \leq n \leq 36) \end{aligned}$ なる数列 ${{a^{(3)}}_{n}}$ において、 $Z ({{a^{(3)}}_{n}}) = Z ({{b^{(2)}}_{n}})$ となります（行間注意）。

${{b^{(3)}}_{n}} = M_{32, 33} (M_{14, 16} (M_{12, 13} (M_{11, 12} (M_{9, 14} (M_{9, 12} ({{a^{(3)}}_{n}}))))))$
を定めれば、
$\begin{aligned} {{b^{(3)}}_{n}} = & 294, 350, 238, 338, 306, 2, 358, 54, 282, 294, 202, 214, \\ 258, 78, 46, 226, 270, 346, 314, 150, 194, 302, 10, 58, \\ 34, 22, 114, 102, 14, 330, 134, 166, 90, 122, 158, 66 \end{aligned}$
をみたします。
${\begin{aligned} Z_{13, 14} ({{b^{(3)}}_{n}}) & = z^{258} + z^{78} = 0 \\ Z_{15, 16} ({{b^{(3)}}_{n}}) & = z^{46} + z^{226} = 0 \\ Z_{9, 12} ({{b^{(3)}}_{n}}) & = z^{{b^{(3)}}_{12}} + z^{{b^{(3)}}_{11}} + z^{{b^{(3)}}_{10}} + z^{{b^{(3)}}_{9}} \\ = - Z_{25, 28} ({{b^{(3)}}_{n}}) \\ Z_{17, 21} ({{b^{(3)}}_{n}}) & = z^{{b^{(3)}}_{21}} + z^{{b^{(3)}}_{20}} + z^{{b^{(3)}}_{19}} + z^{{b^{(3)}}_{18}} + z^{{b^{(3)}}_{17}} \\ = - Z_{29, 33} ({{b^{(3)}}_{n}}) \end{aligned}$
を簡単に確認できるので、すべて足し合わせて $Z_{9, 21} ({{b^{(3)}}_{n}})$ $+ Z_{25, 33} ({{b^{(3)}}_{n}})$ $= 0$ です。ゆえに、 ${c^{(3)}}_{n} = {\begin{aligned} {b^{(3)}}_{n} (1 \leq n \leq 8) \\ {b^{(3)}}_{n + 13} (9 \leq n \leq 11) \\ {b^{(3)}}_{n + 22} (12 \leq n \leq 14) \end{aligned}$ という数列 ${{c^{(3)}}_{n}}$ に関し $Z ({{c^{(3)}}_{n}}) = Z ({{b^{(3)}}_{n}})$ です。数列の項数が22項も一気に減りました。
$\begin{aligned} {{c^{(3)}}_{n}} = & 294, 350, 238, 338, 306, 2, 358, 54, 302, 10, 58, 122, 158, 66 \end{aligned}$

　いよいよ仕上げです。 ${{d^{(3)}}_{n}}$ $= M_{10, 11} (M_{11, 13} (M_{9, 11} ({{c^{(3)}}_{n}})))$ とすると、 $Z_{12, 13} ({{d^{(3)}}_{n}})$ $= z^{122} + z^{302}$ $= 0$ が成立します。すなわち、 ${a^{(4)}}_{n} = {\begin{aligned} {d^{(3)}}_{n} (1 \leq n \leq 11) \\ {d^{(3)}}_{n + 2} (n = 12) \end{aligned}$ で数列 ${{a^{(4)}}_{n}}$ を作れば、これまで通り $Z ({{a^{(4)}}_{n}}) = Z ({{d^{(3)}}_{n}})$ が言えます。
$\begin{aligned} {{a^{(4)}}_{n}} = & 294, 350, 238, 338, 306, 2, 358, 54, 58, 158, 10, 66 \end{aligned}$
　 ${b^{(4)}}_{n}$ $= M_{5, 10} (M_{3, 12} ({a^{(4)}}_{n}))$ とおきましょう。
$\begin{aligned} {{b^{(4)}}_{n}} = & 294, 350, 66, 10, 306, 2, 358, 54, 58, 158, 338, 238 \end{aligned}$
改めて $z^{360} = 1$ を思い出すと、 $z^{{b^{(4)}}_{3}} = \overset{―}{z^{{b^{(4)}}_{1}}},$ $z^{{b^{(4)}}_{4}} = \overset{―}{z^{{b^{(4)}}_{2}}},$ $z^{{b^{(4)}}_{7}} = \overset{―}{z^{{b^{(4)}}_{6}}},$ $z^{{b^{(4)}}_{8}} = \overset{―}{z^{{b^{(4)}}_{5}}}$ に気づきますね。また、
$Z_{9, 12} ({{b^{(4)}}_{n}}) = (z^{158} + z^{58}) (z^{180} + 1) = 0$
です。よって、
$\begin{aligned} Z ({{b^{(4)}}_{n}}) & = Z_{1, 8} ({{b^{(4)}}_{n}}) + Z_{9, 12} ({{b^{(4)}}_{n}}) \\ = z^{{b^{(4)}}_{1}} + z^{{b^{(4)}}_{2}} + \overset{―}{z^{{b^{(4)}}_{1}}} + \overset{―}{z^{{b^{(4)}}_{2}}} + z^{{b^{(4)}}_{5}} + z^{{b^{(4)}}_{6}} + \overset{―}{z^{{b^{(4)}}_{6}}} + \overset{―}{z^{{b^{(4)}}_{5}}} + 0 \\ = z^{{b^{(4)}}_{1}} + z^{{b^{(4)}}_{2}} + z^{{b^{(4)}}_{5}} + z^{{b^{(4)}}_{6}} + \overset{―}{z^{{b^{(4)}}_{1}} + z^{{b^{(4)}}_{2}} + z^{{b^{(4)}}_{5}} + z^{{b^{(4)}}_{6}}} = (実数) \end{aligned}$
を証明できます。これまでの操作を顧みれば $Z ({{a^{(0)}}_{n}})$ $= Z ({{b^{(4)}}_{n}})$ ですから、 $Z ({{a^{(0)}}_{n}})$ も実数である、つまり $\arg Z ({a_{n}}) = {- 16}^{\circ}$ であることが~~やっと~~明かされました。

裏計算まとめ

$\begin{aligned} {a_{n}} = & 278, 334, 266, 210, 290, 346, 278, 222, 322, 266, 198, 254, 342, 38, 242, 186, 86, 30, \\ 354, 298, 62, 330, 286, 18, 42, 134, 178, 86, 98, 6, 142, 50, 150, 58, 14, 106 \end{aligned}$
において、定義2で定めた関数 $M$ を利用し
$\begin{aligned} {a^{(0)}}_{n} = (a_{n} + 16) % 360 \\ {{a^{(1)}}_{n}} = M_{31, 35} (M_{28, 30} (M_{24, 27} (M_{19, 20} (M_{20, 21} (M_{12, 17} (M_{3, 6} ({{a^{(0)}}_{n}}))))))) \\ {{b^{(1)}}_{n}} = M_{34, 36} (M_{20, 22} (M_{18, 19} (M_{17, 18} (M_{10, 11} (M_{7, 8} (M_{5, 9} ({{a^{(1)}}_{n}})))))))) \\ {a^{(2)}}_{n} = {\begin{aligned} {b^{(1)}}_{n} (1 \leq n \leq 10) \\ {b^{(1)}}_{n + 2} (11 \leq n \leq 34) \end{aligned} \\ {{b^{(2)}}_{n}} = M_{20, 23} (M_{7, 14} (M_{3, 6} ({{a^{(2)}}_{n}}))) \\ {a^{(3)}}_{n} = {\begin{aligned} {b^{(2)}}_{n} (1 \leq n \leq 28) \\ {μ^{'}}_{n - 28} (29 \leq n \leq 32) \\ {b^{(2)}}_{n - 2} (33 \leq n \leq 36) \end{aligned} ({{μ^{'}}_{n}} = 14, 330, 134, 90) \\ {{b^{(3)}}_{n}} = M_{32, 33} (M_{14, 16} (M_{12, 13} (M_{11, 12} (M_{9, 14} (M_{9, 12} ({{a^{(3)}}_{n}})))))) \\ {c^{(3)}}_{n} = {\begin{aligned} {b^{(3)}}_{n} (1 \leq n \leq 8) \\ {b^{(3)}}_{n + 13} (9 \leq n \leq 11) \\ {b^{(3)}}_{n + 22} (12 \leq n \leq 14) \end{aligned} \\ {{d^{(3)}}_{n}} = M_{10, 11} (M_{11, 13} (M_{9, 11} ({{c^{(3)}}_{n}}))) \\ {a^{(4)}}_{n} = {\begin{aligned} {d^{(3)}}_{n} (1 \leq n \leq 11) \\ {d^{(3)}}_{n + 2} (n = 12) \end{aligned} \\ {b^{(4)}}_{n} = M_{5, 10} (M_{3, 12} ({a^{(4)}}_{n})) \end{aligned}$
とすれば、 $Z ({{b^{(4)}}_{n}})$ が実数となり、これは $\arg Z ({a_{n}}) = {- 16}^{\circ}$ と同値です。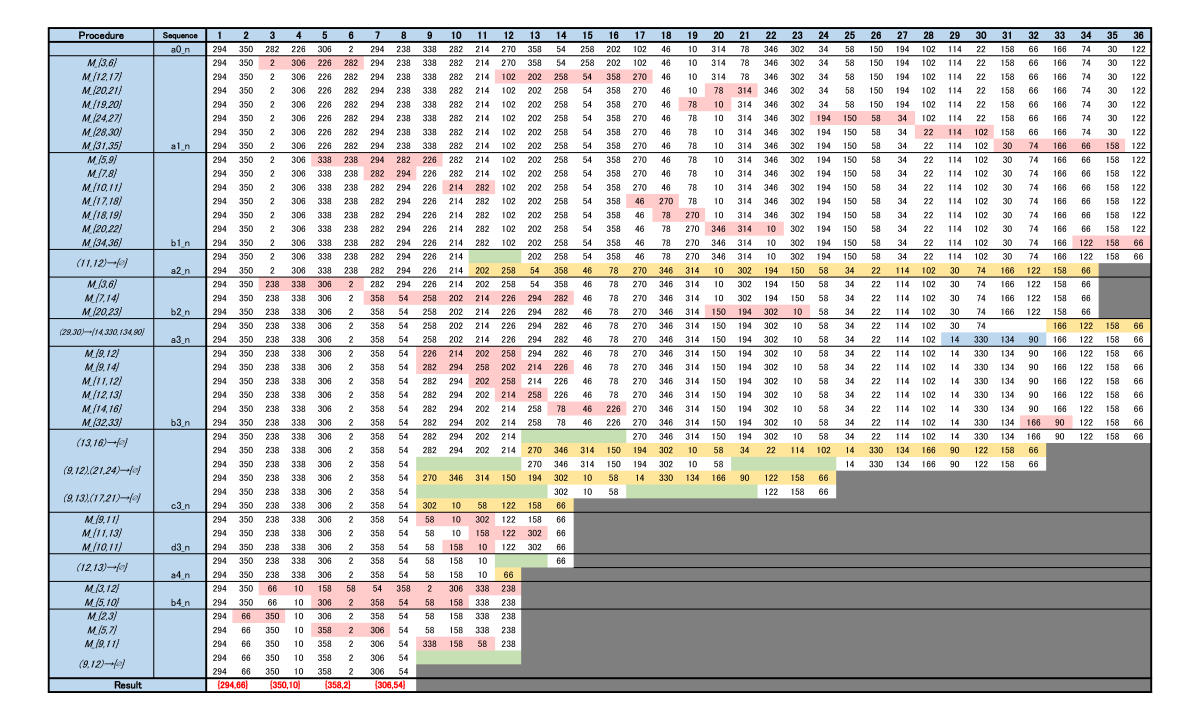

　裏計算が1枚で分かる表も掲載しておきます（最初にこの表を載せるべきでは？）。

計算を初等幾何へ反映させる

　待望の幾何セクションです。2点 $A, D$ を結ぶ折れ線 $P_{0} P_{1} P_{2} \dots P_{36}$ に再度注目します。

数列の和と折れ線の対応（独自の呼称）

　有限数列 ${F_{n}}$ $(1 \leq n \leq N)$ に対し、点列 $S_{0}, S_{1}, S_{2}, \dots, S_{N}$ が
${\begin{aligned} S_{0} S_{1} = S_{1} S_{2} = \dots = S_{N - 1} S_{N} \\ (S_{i - 1} S_{i} の偏角) = {F_{i}}^{\circ} (1 \leq i \leq N) \end{aligned}$
を満足するとき、 $S_{0}, S_{1}, S_{2}, \dots, S_{N}$ をこの順に結んで得られる折れ線 $S$ $= S_{0} S_{1} S_{2} \dots S_{N}$ は $Z ({F_{n}})$ に対応する折れ線であると考える。ただし、偏角の基準となる直線は事前に定まっているものとする。

　利便性のために定義を拵えました。具体例を挙げれば、本問の折れ線 $P_{0} P_{1} P_{2} \dots P_{36}$ は $Z ({a_{n}})$ に対応していますね。

　先程の裏計算で定義した関数 $M$ を、幾何的にとらえてみましょう。いま、八角形 $P_{2} P_{3} P_{4} P_{5}$ $P_{6} Q_{1} Q_{2} Q_{3}$ が点対称な図形となるように3点 $Q_{1}, Q_{2}, Q_{3}$ をとります。すると、 $P_{2} P_{3}$ → $P_{3} P_{4}$ → $P_{4} P_{5}$ → $P_{5} P_{6}$ という経路と $P_{2} Q_{3}$ → $Q_{3} Q_{2}$ → $Q_{2} Q_{1}$ → $Q_{1} P_{6}$ という経路は、始点と終点が一致し、通る線分の偏角も逆順に一致しています。つまり、折れ線 $P_{0} P_{1} P_{2}$ $P_{3} P_{4} P_{5}$ $P_{6} P_{7} \dots P_{36}$ と $Z ({a_{n}})$ （ $=$ $z^{a_{n}}$ の総和）が対応する事実より、折れ線 $P_{0} P_{1} P_{2}$ $Q_{3} Q_{2} Q_{1}$ $P_{6} P_{7} \dots P_{36}$ と $Z (M_{3, 6} ({a_{n}}))$ が対応するのです（わずかな行間を読み取ってください）。関数 $M$ は折れ線（の一部）の点対称移動を表していたのですね。
　これを踏まえ、 $Z ({{a^{(1)}}_{n}})$ に対応する折れ線を作り出します。十二角形 $P_{11} P_{12} P_{13} P_{14}$ $P_{15} P_{16} P_{17} Q_{4}$ $Q_{5} Q_{6} Q_{7} Q_{8}$ 、四角形 $P_{19} P_{20} P_{21} Q_{9}$ 、四角形 $P_{18} P_{19} Q_{9} Q_{10}$ 、八角形 $P_{23} P_{24} P_{25} P_{26}$ $P_{27} Q_{11} Q_{12} Q_{13}$ 、六角形 $P_{27} P_{28} P_{29}$ $P_{30} Q_{14} Q_{15}$ 、十角形 $P_{30} P_{31} P_{32}$ $P_{33} P_{34} P_{35}$ $Q_{16} Q_{17} Q_{18} Q_{19}$ がいずれも点対称な図形となるように、 $Q_{4}$ ～ $Q_{19}$ の16点を設けましょう（下図左）。

　新しく用意した多角形のそれぞれについて、折れ線が通る経路を入れ替えます（上図右）。そうすると、新たに生成される経路は
$Z (M_{31, 35} (M_{28, 30} (M_{24, 27} (M_{19, 20} (M_{20, 21} (M_{12, 17} (M_{3, 6} ({a_{n}}))))))))$
に対応し、 ${{a^{(0)}}_{n}},$ ${{a^{(1)}}_{n}}$ の定義からこれは $Z ({{a^{(1)}}_{n} - 16})$ に対応する折れ線です（かなりの行間を読み取ってください）。この折れ線を反時計回りに $16^{\circ}$ 回転させたものが、 $Z ({{a^{(1)}}_{n}})$ に対応する折れ線といえます。

　この調子で、始点と終点を保ったまま折れ線を変形していきます。十角形 $Q_{2} Q_{1} P_{6}$ $P_{7} P_{8} P_{9}$ $Q_{20} Q_{21} Q_{22} Q_{23}$ 、四角形 $Q_{22} Q_{21} Q_{20} Q_{24}$ 、四角形 $P_{17} P_{18} Q_{26} Q_{4}$ 、四角形 $Q_{26} P_{10} Q_{10} Q_{25}$ 、六角形 $Q_{10} Q_{9} P_{21}$ $P_{22} Q_{27} Q_{28}$ 、六角形 $Q_{17} Q_{16} P_{35}$ $P_{36} Q_{29} Q_{30}$ がいずれも点対称な図形となるように、 $Q_{20}$ ～ $Q_{30}$ の11点を設けましょう（下図左）。

　先程と同様に経路変換を行い、 $P_{9} P_{10}$ → $P_{10} P_{11}$ → $P_{11} P_{8}$ という経路を $P_{9} P_{8}$ に直すと（ $∵$ 四角形 $P_{9} P_{10} P_{11} Q_{8}$ は平行四辺形）折れ線は上図右のような形状になります。この折れ線が $Z ({{a^{(2)}}_{n} - 16})$ $= z^{- 16} Z ({{a^{(2)}}_{n}})$ に対応することは、従前の議論と同じ道筋で判りますね。実際には ${{a^{(1)}}_{n}}$ から ${{a^{(2)}}_{n}}$ へ変形する手順をカンニングし、それを根拠に多角形を貼りつけているのですが。

　以下、多角形の名称を書き並べる気力が無くなったので、図から読み取ってください。原則点対称です。 $Q_{31}$ ～ $Q_{43}$ の13点を設けます。また、六角形 $P_{30} Q_{19} Q_{18}$ $Q_{44} Q_{45} Q_{46}$ が $120^{\circ}$ 回転で自身と重なる図形となるように $Q_{44}$ ～ $Q_{46}$ の3点を設けます（ただし $Q_{19} Q_{44} < Q_{19} Q_{18}$ とする）。ここまでを行い、いつも通り経路を変換したものが下図です。これで $z^{- 16} Z ({{a^{(3)}}_{n}})$ に対応する折れ線が作られます。

　 ${{a^{(3)}}_{n}}$ から ${{a^{(4)}}_{n}}$ へ変形する手順を参考に、どんどん経路を変えていきます。点対称の原則を守りつつ $Q_{44}$ ～ $Q_{55}$ の12点を設け、経路変換と（同じ道を行って戻る経路の）削除を適宜行えば、下図のように折れ線が移ります。

　折れ線 $Q_{39} Q_{53}$ $Q_{52} Q_{54} Q_{25}$ と折れ線 $P_{30} Q_{14}$ $Q_{15} P_{27} Q_{11}$ は平行移動で重なるため（計算略）、 $Q_{39} Q_{25} = P_{30} Q_{11}$ です。また、折れ線 $Q_{25} Q_{10} Q_{28}$ $Q_{27} Q_{43} Q_{42}$ と折れ線 $Q_{17} Q_{55} Q_{44}$ $Q_{45} Q_{46} P_{30}$ も平行移動で重なり、 $Q_{25} Q_{42} = Q_{17} P_{30}$ を得ます（下図左）。ついでに $Q_{42} Q_{41} / / Q_{30} Q_{17}$ です。
　ということは、十角形 $Q_{39} Q_{25} Q_{42}$ $Q_{41} Q_{12} Q_{11}$ $P_{30} Q_{17} Q_{30} Q_{56}$ が点対称な図形となるように、点 $Q_{56}$ をとることができますね。四角形 $Q_{56} Q_{30} Q_{29} Q_{57}$ がひし形となるような点 $Q_{57}$ もとっておくと、長かった経路が下図右のように短縮されます。これが $z^{- 16} Z ({{a^{(4)}}_{n}})$ に対応する折れ線です。

　あとはどうとでもなります。 $△ Q_{32} Q_{22} Q_{39}$ が二等辺三角形であることに注目し、線分 $Q_{32} Q_{39}$ の偏角が ${- 16}^{\circ}$ であると判ります。また $P_{2} Q_{32} = Q_{57} Q_{39}$ かつ $P_{2} Q_{32} / / Q_{57} Q_{39}$ から、線分 $P_{2} Q_{57}$ の偏角も ${- 16}^{\circ}$ です。すると $∠ P_{1} P_{2} Q_{57}$ $= ∠ Q_{29} Q_{57} P_{2}$ が成立し、四角形 $P_{0} P_{2} Q_{57} P_{36}$ は $P_{0} P_{2} = P_{36} Q_{57}$ の等脚台形といえます。以上より、線分 $P_{0} P_{36}$ の偏角、すなわち線分 $A D$ の偏角は ${- 16}^{\circ}$ なのです。
　いま、線分 $E D$ の偏角は $34^{\circ}$ ですから、最終的に $∠ A D E$ $= 50^{\circ}$ が確定しました。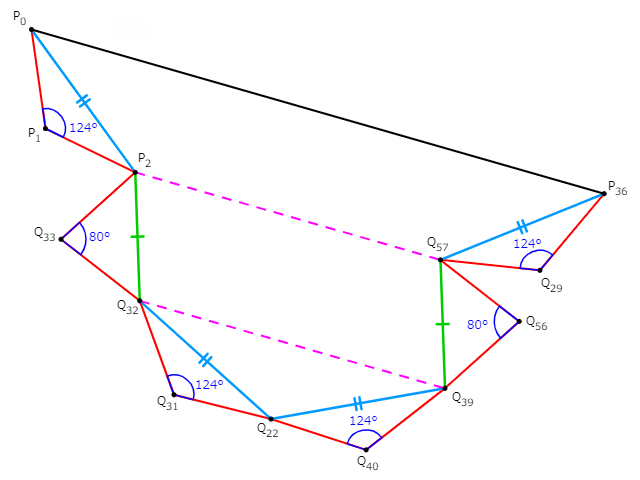

Frequently Asked Question

Ｑ．数列の項の入れ替え方をどうやって思いつけば……
Ａ．転倒数の考え方を用いましょう

　ここまで読んだ多くの読者は、各自で二段整角四角形問題を作り、経路変換を試みていることでしょう。しかしながら、ただ闇雲に折れ線の平行移動を繰り返すだけでは、図が複雑になっていくのみです。もっとシステマティックに変換しなければなりません。~~えっ、そもそも試みてなどいない？　おかしいですね……。~~
　今からその手順をお伝えします。例として、以下の数列 ${ρ_{n}}$ を持ってきました。
${ρ_{n}} = - 82, - 30, - 18, 142, 22, 54$
　 $Z ({ρ_{n}})$ が実数であることを確かめましょう。まず、
$\begin{aligned} z^{- 30} + z^{- 18} + z^{54} - (\overset{―}{z^{- 30} + z^{- 18} + z^{54}}) \\ = z^{- 30} + z^{- 18} + z^{54} + z^{- 150} + z^{- 162} + z^{126} \\ = (z^{- 150} + z^{- 30} + z^{90}) + (z^{- 162} + z^{- 90} + z^{- 18} + z^{54} + z^{126}) = 0 \end{aligned}$
より、 $z^{- 30} + z^{- 18} + z^{54}$ は実数です。また、 $z^{142} + z^{22} + z^{- 98}$ も実数ですから、
$\begin{aligned} Z ({ρ_{n}}) & = z^{- 82} + z^{142} + z^{22} + (z^{- 30} + z^{- 18} + z^{54}) \\ = z^{- 82} - z^{- 98} + (z^{142} + z^{22} + z^{- 98}) + (実数) \\ = z^{- 82} + z^{82} + (実数) + (実数) = (実数) \end{aligned}$
という風に確かめられました。よって、 ${ρ_{n}}$ の先頭に $82, - 98$ を追加した数列 ${{ρ^{'}}_{n}}$ を用意し、
${{ρ^{'}}_{n}} = 82, - 98, - 82, - 30, - 18, 142, 22, 54$
から $(82, - 82),$ $(- 98, 142, 22),$ $(- 30, - 18, 54)$ の形を見つけられるように関数 $M$ を適用することが目標となります。

${{ρ^{″}}_{n}} = 82, - 82, - 98, 142, 22, - 30, - 18, 54$
は ${{ρ^{'}}_{n}}$ の項を並べ替えた数列であり、かつ $(82, - 82),$ $(- 98, 142, 22),$ $(- 30, - 18, 54)$ の形が非常に見やすいです。
${{ρ^{'}}_{n}} = {ρ^{″}}_{1}, {ρ^{″}}_{3}, {ρ^{″}}_{2}, {ρ^{″}}_{6}, {ρ^{″}}_{7}, {ρ^{″}}_{4}, {ρ^{″}}_{5}, {ρ^{″}}_{8}$
ですから、この添字だけを抽出した新たな数列 ${σ_{n}}$ は ${σ_{n}}$ $= 1, 3, 2, 6,$ $7, 4, 5, 8$ となります。
　 ${σ_{n}}$ について転倒数（inversion number）を計算してみると、その値は $5$ です。試しに $M_{4, 6} ({σ_{n}})$ という数列の転倒数も計算すると、その値は $3$ になります。数列 $1, 2, \dots, 8$ の転倒数は当然 $0$ ですから、 ${σ_{n}}$ と $M_{4, 6} ({σ_{n}})$ を比較すれば、後者のほうが数列 $1, 2, \dots, 8$ に「近い」といえますね。換言すると、 ${{ρ^{'}}_{n}}$ と $M_{4, 6} ({{ρ^{'}}_{n}})$ では後者のほうが数列 ${{ρ^{″}}_{n}}$ $= {ρ^{″}}_{1}, {ρ^{″}}_{2}, \dots, {ρ^{″}}_{8}$ に「近い」のです（行間……）。
　このように、「添字の転倒数を $0$ に近づける」というコンセプトを抱きつつ関数 $M$ を用いれば、有限回の関数合成で ${{ρ^{'}}_{n}}$ は ${{ρ^{″}}_{n}}$ に変換されます。もとの数列の転倒数が $0$ でない限り、転倒数が減少するような適用方法は必ず存在するためです（詳しくは「バブルソート交換回数」などで検索してください）。今回であれば、 $M_{2, 3} (M_{5, 7} (M_{4, 6} ({{ρ^{'}}_{n}})))$ と操作することで ${{ρ^{″}}_{n}}$ と完全に一致させられます。

　問題1では、これと同じことを36項もの数列で行いました。ゴールとなる順序を仮定し、計算してみた添字の転倒数はなんと $116$ （この値はゴール次第で変動します）。 $116$ 回以内の関数合成で変換を終えられるという事実に大歓喜……できるわけもなく無事心が折れ、効率的に転倒数を減らす交換方法をPython先生へとお尋ねしました。やはり先生は優秀でして、ものの数秒で全探索を終え20回台の合成手順を提出されたのですが、幾何に還元した際の図の見やすさなども慮った結果、本記事に掲載したとおりの28回の交換（with 項の追加や除去）を採用するに至ったのです。実は28回でも結構削ったほうなのですよ……。

Impractical Practice Problems

　凸四角形 $A B C D$ の辺 $A B, C D$ 上にそれぞれ点 $E, F$ をとると、 $∠ A B F = a^{\circ},$ $∠ C B F = b^{\circ},$ $∠ E C B = c^{\circ},$ $∠ E C D = d^{\circ},$ $∠ A F B = e^{\circ},$ $∠ D E C = f^{\circ}$ が成立した。このとき $∠ A D E$ の大きさは度数法で整数値となるが、その値を求めなさい。
$\begin{aligned} (1) (a, b, c, d, e, f) = (58, 28, 19, 65, 34, 53) \\ (2) (a, b, c, d, e, f) = (64, 38, 24, 68, 52, 56) \\ (3) (a, b, c, d, e, f) = (44, 38, 34, 22, 78, 88) \end{aligned}$

　 $(1)$ は前回例示した二段整角四角形ですね。つまり、外心10個法~~などという煩雑極まりないメソッド~~に頼らずとも解けます。 $(3)$ は外心10個法以外の初等幾何解法を発見できていません（本記事投稿日現在）。

The Confused Conclusion

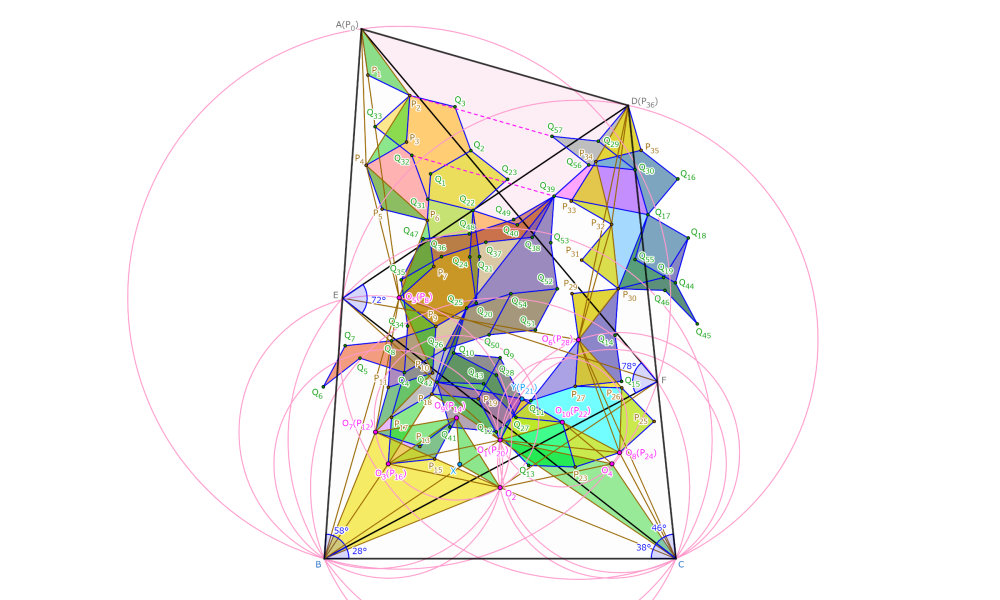
　お疲れ様でした。問題1の解答に用いた補助オブジェクトを上図にまとめたので、これで癒されてください。どことなくステンドグラスっぽくないですか？（主観）
　ちなみに、プログラムを組んで数えてみると、補助点が95個、補助円が10個、そして補助線が176本でした。前々回の記録を早くも超えてしまいました……。

　さて、以上の議論によって二段整角四角形問題（当然のように連呼していますがあくまで独自の呼称です）を完全解決した次第ですが、実のところ、「外心10個法」にはある問題点があります。
　問題2へ果敢に挑んでくださった読者ならば、恐らくお気づきのことでしょう。そう、本メソッドに従って折れ線を描いたとき、 $P_{0}$ ～ $P_{8}$ の区間と $P_{24}$ ～ $P_{28}$ の区間からそれぞれ1本ずつ選んだ線分の組で、ちょうど逆向きのものが少なくとも1組存在するのです。 $P_{8}$ ～ $P_{12}$ の区間と $P_{28}$ ～ $P_{36}$ の区間にも、同様の組が必ず存在します。
　長さが等しく向きが逆のベクトルは相互に打ち消しあうので、何らかの手順を加えることにより、はじめから三十二等辺三十三角形として議論を開始できるはずなのです。現行の三十六等辺三十七角形は過剰な複雑さを有するといえます。つまるところ、手法が洗練されていなかったのです。

　だからこそ。この問題点を独力で解決できなかったからこそ、私は本記事を書き上げました。私よりも数学への造詣が深い読者から、ソリューションを与えていただくためです。
　 aerile_re 氏が「外心3つ法」を発見したときも、もとは外心を2つしかとっていなかったそうです。しかしながら、2つの外心では（1組の線分が打ち消しあう）八等辺九角形が得られてしまい、それを解消すべく試行錯誤した結果、3つ目の外心を発見したといいます。帰納的に、私の提唱する「外心10個法」では、さらに1～2個の外心をどこかにとることで、真に洗練された三十二等辺三十三角形を得ると考えられます。本来「外心11個法」あるいは「外心12個法」であるべきなのでしょう。
　ですが、記事投稿日までの私には、それらの外心が見えませんでした。GeoGebraで数百個の外心を作図すれども、ただWindowsの挙動が遅くなるだけに終わりました。
　皆様、お力添えをいただけませんか？

【前編と後編のまとめ】

$\cdot$ 任意の二段整角四角形問題は「外心10個法」により初等的に解かれる
$\cdot$ 36本もの線分からなる経路を偏角が自明な経路に変換するのは非常に大変である
$\cdot$ 現行の「外心10個法」は粗削りであり改善を要する

It's Time for "Yodan"

　前編の投稿からわずか数時間で“ご本人”が降臨しました。解りますよ、自身で編み出した手法を別の誰かが語っていれば、内容云々の前に反応したくなるものです。私もレムニスケート関連で同様の経験が複数回あります。ですが流石に早すぎませんか？

　もう1件、第４回匿式図形問題エスパー杯の解説記事（問題Ａ～Ｅ・問題Ｆ）に2024年7月21日現在計12件の高評価をいただいております。誠にありがとうございます。今後とも変わらぬご愛顧を……。