文献あり

第４回匿式図形問題エスパー杯（T-GUESS Cup 4）　問題Ｆの解説

589

　2024年5月3日～5月8日にかけて『第４回匿式図形問題エスパー杯 (T-GUESS Cup 4: Tock's Geometry "Using Extra-Sensory Solutions" Cup The 4th)』を開催しました。本記事では、その最終問題である問題Ｆの紹介および解説を行います。高難度の幾何に翻弄されましょう。なお、問題Ａ～問題Ｅの解説はこちらの記事にて行っています。興味があればお読みください。
　コンテストに出場していない方も、「こんな性質が成り立っているのか」という気持ちで読んでいけるはずです。この1問に大量の知識がオムニバスされているので。

問題紹介

（問題Ｆ）

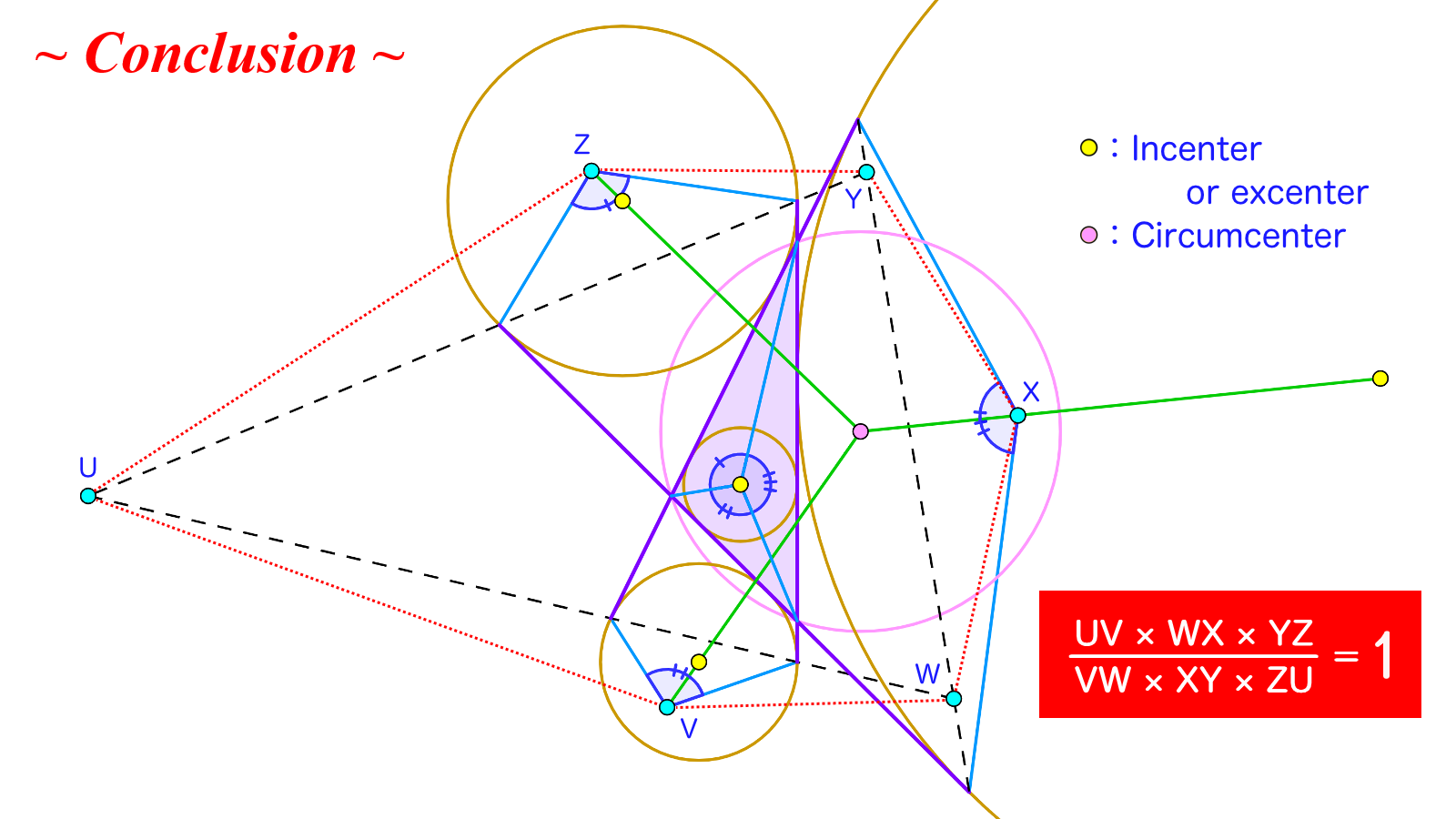
　$\triangle ABC$の外心を$O$、内心を$I$とする。$\angle A$内の傍接円と傍心をそれぞれ$\omega_A, I_A$とし、$\omega_A$と半直線$AB,AC$の接点を$T_{AB},T_{AC}$とおく。同様に$\omega_B, \omega_C,$$I_B, I_C,$$T_{BC},T_{BA},$$T_{CA},T_{CB}$も定める。点$U,W,Y$はそれぞれ$T_{BC}T_{BA}$と$T_{CA}T_{CB}$、$T_{CA}T_{CB}$と$T_{AB}T_{AC}$、$T_{AB}T_{AC}$と$T_{BC}T_{BA}$の交点である。点$V,X,Z$はそれぞれ直線$OI_C,OI_A,OI_B$上の点であり、$\angle T_{CA}VT_{CB}=\angle AIB,$$\angle T_{AB}XT_{AC}=\angle BIC,$$\angle T_{BC}ZT_{BA}=\angle CIA$をみたす（ただし、$V,X,Z$はいずれも$\triangle UWY$の外部にある）。
　このとき、$\dfrac{UV\times WX\times YZ}{VW\times XY\times ZU}$の値を求めなさい。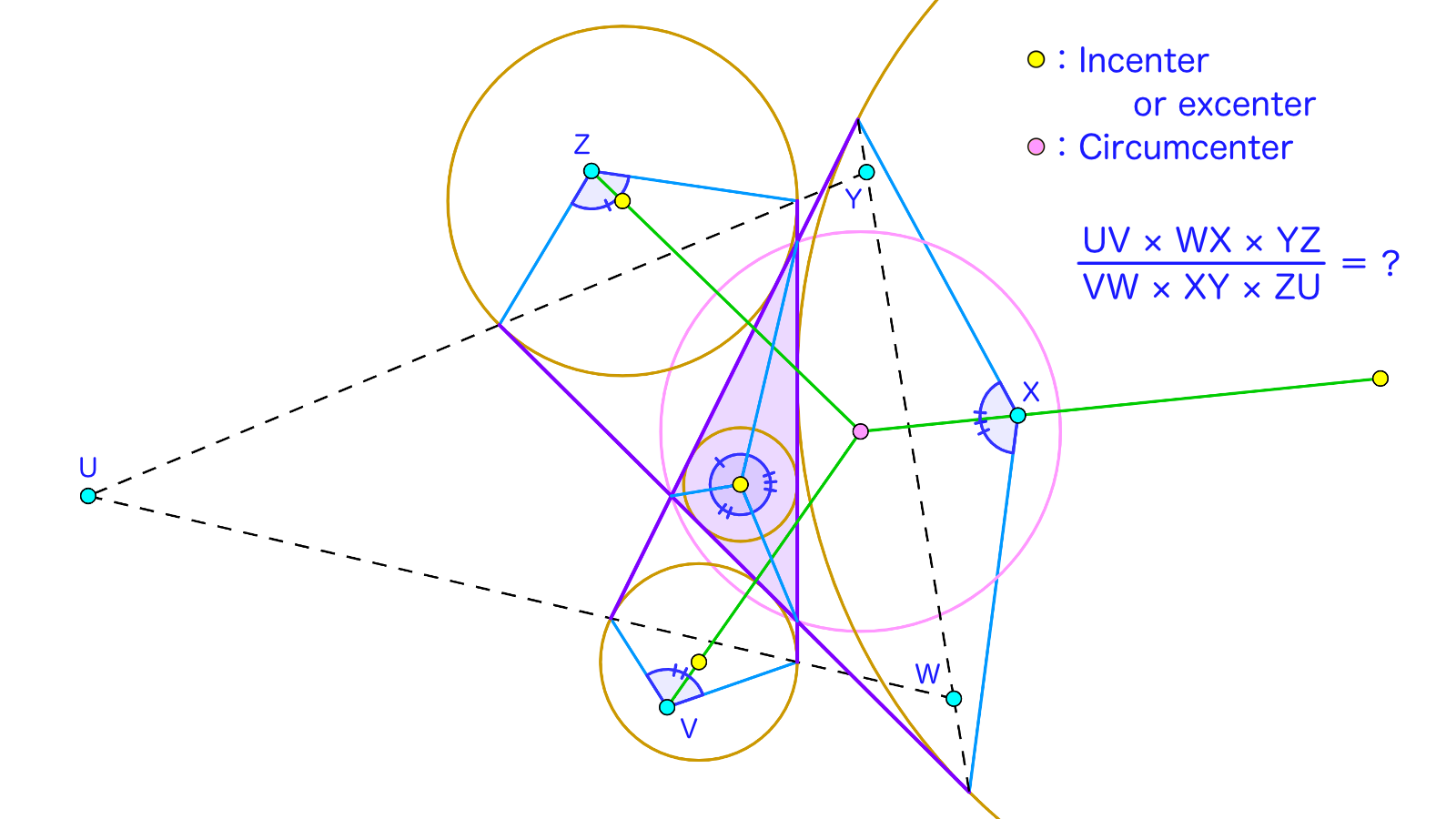

「これは、なんですか？？？？？？」
　本問の印象を一言で述べると、こうなりますね。問題Ａ～Ｅまで数々の難問を打ち破って疲弊した脳にとっては、あまりにも重い一撃です。とにかく定義が多く、内容の理解さえも困難に思えます。問題文の時点で定義を23種類も用いる不親切設計。まず外心・内心・傍心を描いて、外心と傍心を結んで、角度を測って……。

　唯一の救いは、問われている式が特徴的な形をしていることですね。$\dfrac{UV\times WX\times YZ}{VW\times XY\times ZU}$という形は、有名なチェバの定理やメネラウスの定理を連想させます。これらの定理では、比の積が$1$になっていました。ということは、今回解くべき問題も、きっと最終的に$1$が出てくるのでしょう。仮に本問の答えが$1$よりも大きい定数ならば、$V$と$Z$、$W$と$Y$の名前を入れ替えることで$\dfrac{UV\times WX\times YZ}{VW\times XY\times ZU}$の分母と分子が逆転し、$1$よりも小さな値を得るため仮定に矛盾、といった背理法的な推論も効きます。

いざ挑戦

最初のエスパー

　どこから考察しようか迷いますね。こういった難問は、手の付けどころを見極める時点から難しいものです。
　そこでエスパーです（注：本記事では無根拠の仮定や勘を「エスパー」と呼称します）。本問を作った主催者が、別に賢いわけではないとエスパーしましょう。
　賢くない人間が難問を捻出する方法とは、一体何でしょうか？　少し想像してみれば、答えは自ずと見えてきますね。そうです。既存の難問や定理を色々詰め込んで、強引に難しくしているのです。元となった性質さえ分かれば、あとは簡単な考察で糊付けするだけ、ともいえます。
　その性質の正体を突き止めるところから、我々の戦いが始まります。

2度目のエスパー

　隠れた性質を追うためには、さらなるエスパーが必要です。手がかりは、先述した$\dfrac{UV\times WX\times YZ}{VW\times XY\times ZU}$という式の形。チェバらしさやメネラウスらしさが漂っており、どこかにチェバやメネラウスの使える図形が無いか探したくなります。
　ですが、ここで踏みとどまりましょう。作問者の気持ちになるのです。「チェバやメネラウスの形を露骨に残したまま、最終問題として出題するか？」と考えましょう。ええ、普通の感性であれば、そういう安易な出題はしませんね。「メネラウスだ」と思わせておいて実はメネラウスに頼らない、となるのが一般的です。

　チェバでもメネラウスでもなく、$\dfrac{UV\times WX\times YZ}{VW\times XY\times ZU}$をうまく扱える定理、何を思いつきますか？
　ある程度幾何を浚った方であれば、春木の定理（ Wikipedia ）を思いつくかもしれません。知らない方のために軽く紹介します。

（春木の定理）

　互いに交わる3つの円の交点を図のようにとったとき、$\dfrac{AB\times CD\times EF}{BC\times DE\times FA}=1$が成立する。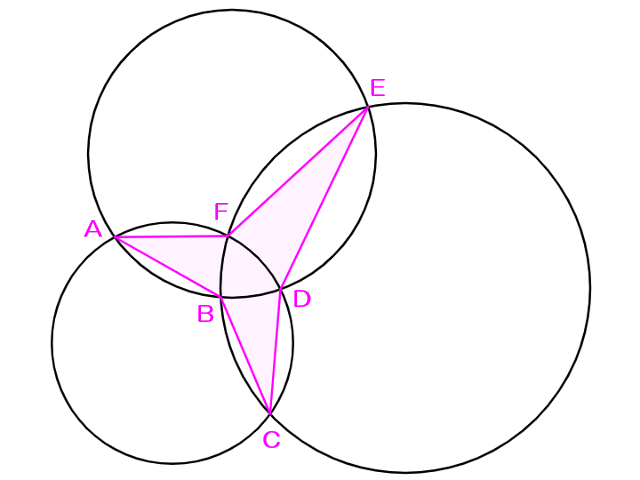

　ビジュアルが良いですね。これを本問に使えないか、しばし試してみましょう。

　　～GeoGebraで作図中～

　収穫がありました。以下をご覧ください。

　春木の定理に概形を似せるため、3点$V,X,Z$をそれぞれ$UW,WY,YU$について対称移動してみました。移動後の点を$V',X',Z'$としてみると、上図のように$(U,W,X',Z'),$$(W,Y,Z',V'),$$(Y,U,V',X')$が共円になっているではありませんか。（「こんな共円見つかるわけないよ」という方は、先程載せた春木の定理の図をもう一度よくご覧ください。割と定理そのままの形です。）
　この事実はあとで証明するとして、さらに考察を深めましょう。

3度目のエスパー

　先程の図をよく見れば、もう少しエスパーできそうなことがありますね。6点$T_{AB},T_{AC},$$T_{BC},T_{BA},$$T_{CA},T_{CB}$が、緑点線で描かれた3円のいずれかに乗っているように見えます。また、3点$V',X',Z'$はいずれも$\triangle ABC$の傍接円上に存在しそうです（こちらの性質は角度計算で簡単に示せます）。
　取っ掛かりの候補が増えてきました。しかしながら、今のままではやや決定打に欠けます。$U,W,Y$という見慣れない点を扱うのは大変なので、どうにかしたいところ……。

　　～GeoGebraで試行錯誤中～

　収穫が増えました。以下をご覧ください。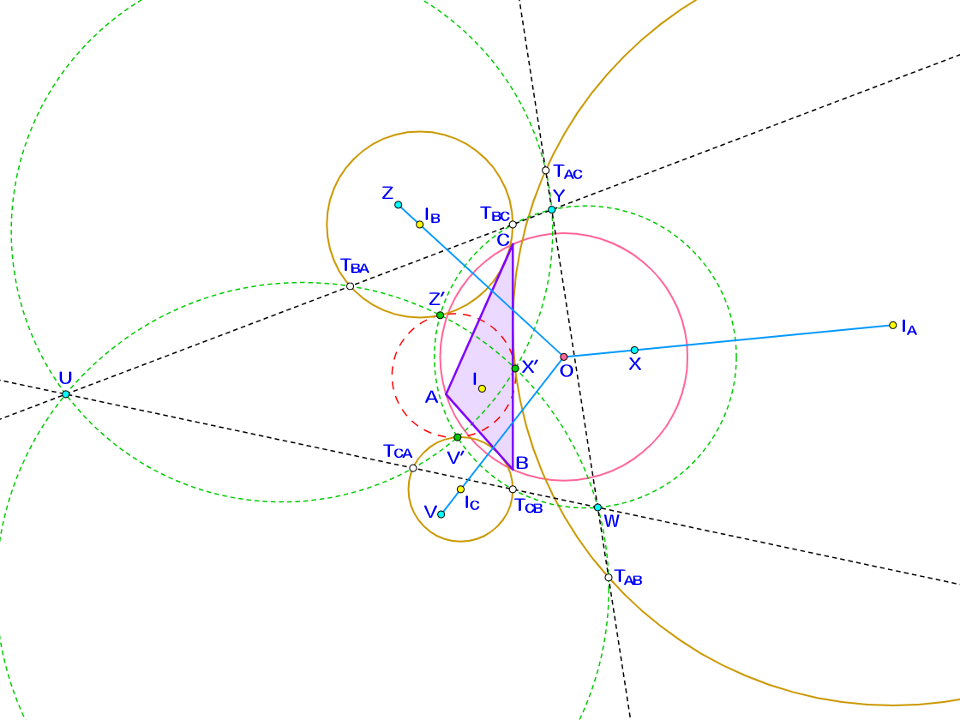

　3点$V',X',Z'$を通る円を作図してみました（赤点線）。すると、この円は$\triangle ABC$の3つの傍接円すべてに外接する模様です。理由は分かりませんが、見た目と直感とGeoGebraがそう言っています。
「それって、つまり……」と察した方も多いでしょう。その通りです。フォイエルバッハの定理( Wikipedia )から、緑点線で描かれた円はすなわち$\triangle ABC$の九点円であり、その接点たる$V',X',Z'$は$\triangle ABC$の外フォイエルバッハ点とエスパーされます。とても強い結果が出てきましたね。
　ここまでを全部エスパーすると、本問は以下のように切り分けられます。

（問題Ｆの部分的解決）

　問題1における$T_{AB},T_{AC},$$T_{BC},T_{BA},$$T_{CA},T_{CB}$$U,W,Y$の定義はそのまま用いる。$\triangle ABC$の$\angle A,\angle B,\angle C$内の外フォイエルバッハ点を$F_A,F_B,F_C$としたとき、$(T_{CA},T_{AC},$$F_C,F_A,$$Y,U),$$(T_{AB},T_{BA},$$F_A,F_B,$$U,W),$$(T_{BC},T_{CB},$$F_B,F_C,$$W,Y)$がそれぞれ同一円周上に存在することを証明しなさい。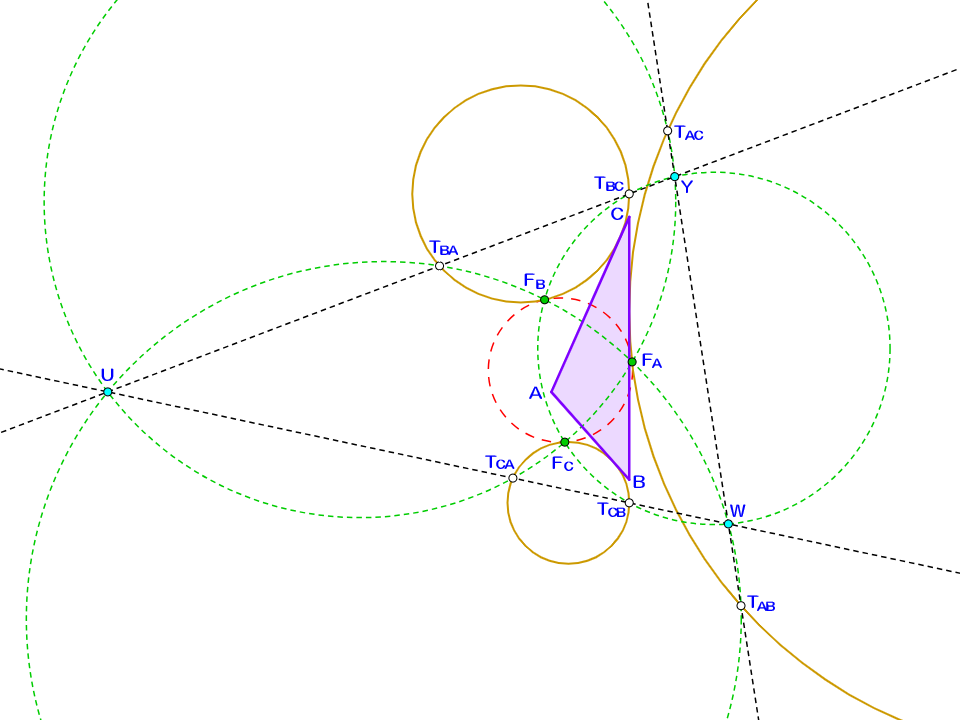

　したがって、ここからは次のような流れで考えていきます。

〈1st step〉	問題2を頑張って証明する。
〈2nd step〉	$V'=F_C,$$X'=F_A,$$Z'=F_B$を示す(難所)。
〈3rd step〉	残りのエスパー部分を論証して総仕上げ。

　前置きが長くなりましたが、いよいよミッション・スタートです。

重い解説

〈1st step〉

　取り敢えず$U,W,Y$の周辺を色々調べると、以下の性質が見つかります。

　傍接円$\omega_A$と辺$BC$との接点を$S_A$と定めると、$AU=I_A S_A$かつ$AU / \! / I_A S_A$である。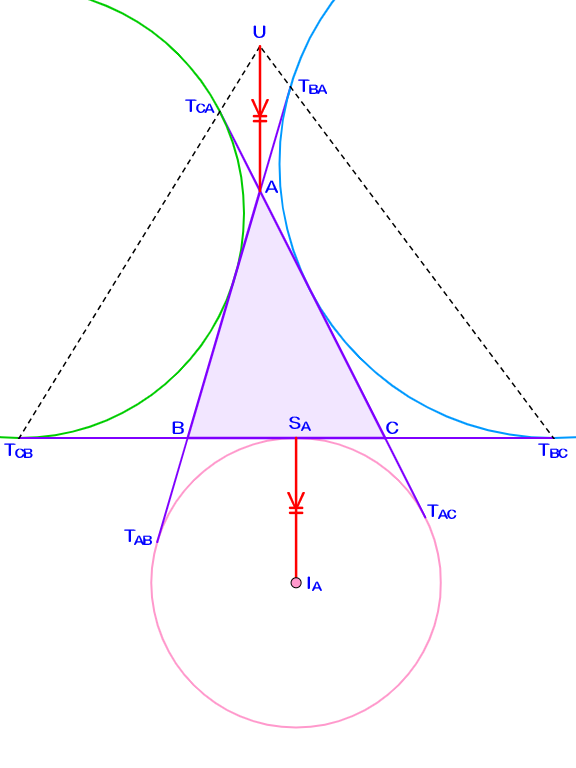

　$A$から$BC$の平行線を引き、$UW,UY$との交点をそれぞれ$P_1,Q_1$とする。明らかに$\triangle AP_1 T_{CA} \sim \triangle CT_{CB} T_{CA}$であるため$AP_1=AT_{CA}$となり、傍接円の性質から$AT_{CA}=CT_{AC}$$=CS_A$も判る。ゆえに$AP_1=CS_A$、同様にして$AQ_1=BS_A$が従う。
　加えて、簡単な角度計算から$UW / \! / CI_A,$$UY / \! / BI_A$を示せる。これらを利用すると、線分$AS_A$の中点$M_1$について$\triangle I_A BC$を点対称移動させれば$\triangle UQ_1 P_1$にぴったり重なることが導かれる。この事実は補題の主張を明瞭に説明する。$\blacksquare$

　たったいま示した補題2を念頭に、次のような構図も考えましょう。

　$\omega_B$と辺$CA$、$\omega_C$と辺$AB$との接点をそれぞれ$S_B,S_C$と定める。点$W_2$は$BW_2=I_C S_C$をみたす直線$WB$上の点であり、$B$に関して$W$の反対側にある。点$Y_2$は$CY_2=I_B S_B$をみたす直線$YC$上の点であり、$C$に関して$Y$の反対側にある。
　このとき、6点$(W,W_2,$$Y,Y_2,$$T_{BC},T_{CB})$はある1つの円に乗る。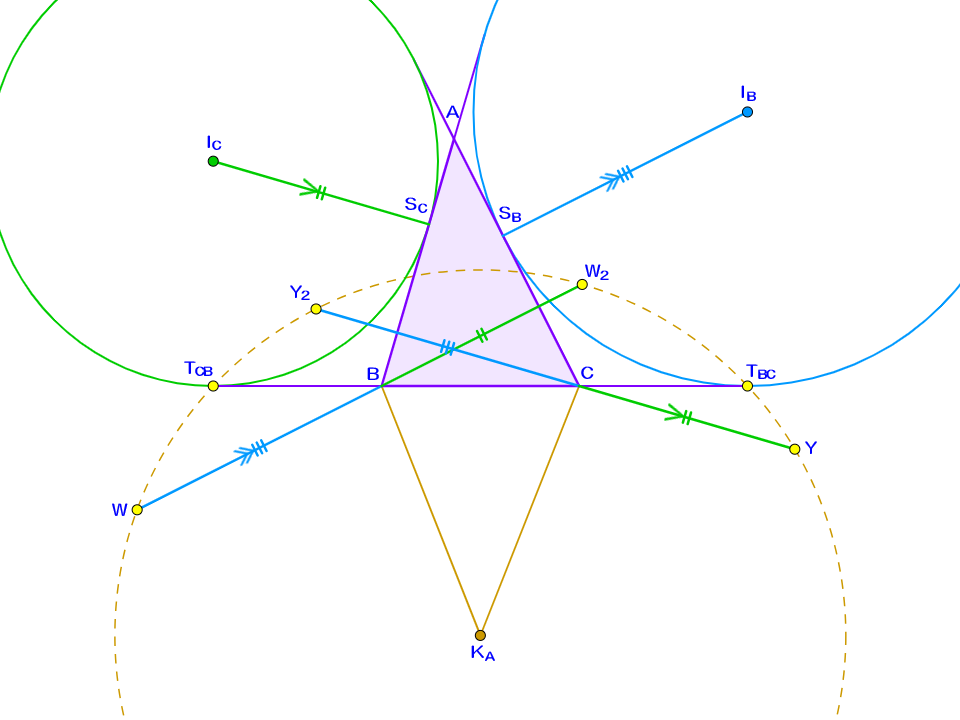

　線分$I_B I_C$の中点を$M_2$とする。$\triangle ABC$の外接円と$\triangle I_A I_B I_C$の九点円は一致するので、$M_2$は$\triangle ABC$の外接円に乗っている。ここから$\angle BM_2 C=\angle BAC$が判る。また、$\angle I_B BI_C=\angle I_B CI_C$$={90}^{\circ}$より4点$(B,C,$$I_B,I_C)$は共円であり、特に$M_2 I_B=M_2 B$$=M_2 C$$=M_2 I_C$を得る。
　いま、$M_2$を直線$BC$に関して対称移動した点を$K_A$とおくと、当然ながら$K_A B=K_A C$$=M_2 C$$=M_2 I_B$である。ゆえに、補題2を用いつつ軽めの角度計算を挟めば、$\triangle K_A BW \equiv \triangle M_2 I_B T_{BC}$を示すことができる。この合同から$K_A W=M_2 T_{BC}$$=K_A T_{BC}$が従うので、2点$W,T_{BC}$はいずれも$K_A$からの距離が等しい。同様の考察を繰り返せば、6点$(W,W_2,$$Y,Y_2,$$T_{BC},T_{CB})$はいずれも$K_A$からの距離が等しいと判明する。$\blacksquare$

　余談ですが、$\triangle ABC$の垂心を$H$とすると$HW=HY$になっています。補題3の証明を追えば理解できると思うので、演習問題にどうぞ。

〈1st step〉の仕上げです。補題3にて4点$(W,Y,$$T_{BC},T_{CB})$の乗る円を見つけられたので、この円が$F_B,F_C$も通ることを示せば問題2を証明できますね。そのためには、$K_A F_B=K_A T_{BC}$を導けると良さそうです。
　行きましょう。天啓を享け、下図のように放物線を描いてみます。

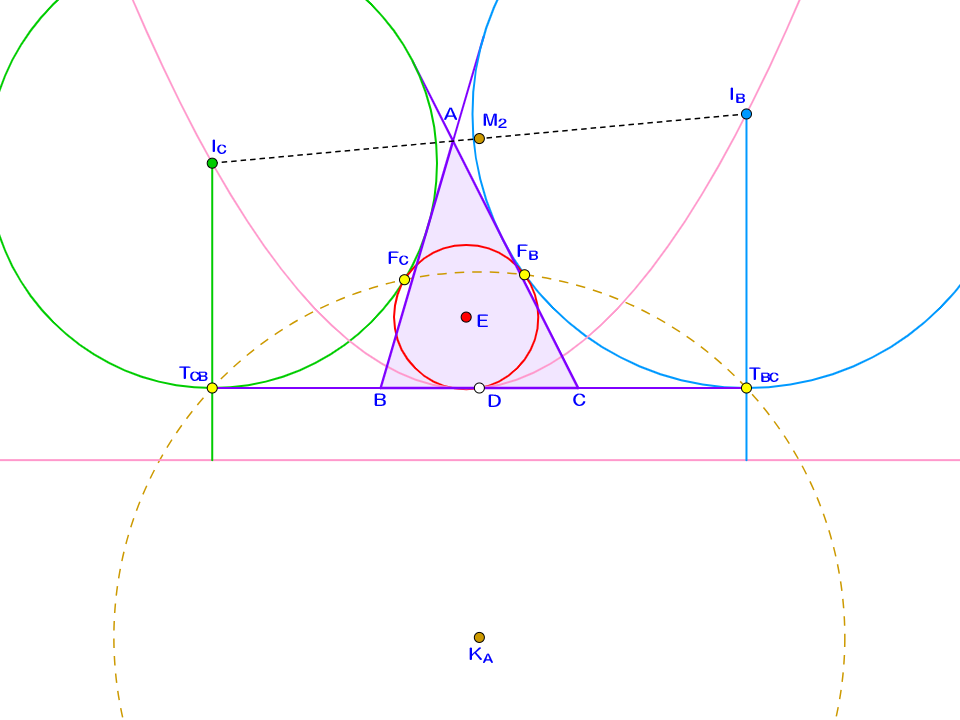
「また変なこと始めたよこの人……」
　少なからぬブーイングが聞こえますね。恐ろしや恐ろしや……。
　そもそもこれがどういう放物線なのか、そこから説明しましょう。まず$\triangle ABC$において、辺$BC$の中点を$D$、九点円の中心を$E$としました。次に、直線$BC$を点$A$と反対側に距離$DE$だけ移動させた直線$l$を用意しました。ここに、焦点が$E$、準線が$l$である放物線$p$は3点$I_B,I_C,D$を通っている、という性質が生まれるのです。
　発想さえあれば、示すのは簡単です。放物線は焦点からと準線からの距離が等しい点の軌跡なので、3点$I_B,I_C,D$について$E$からの距離と$l$からの距離を比較するとよいですね。例えば$I_B$に注目し、$I_B T_{BC}$と$l$の交点を$L_B$とおくと、$I_B E=I_B F_B+F_B E$$=I_B T_{BC}+T_{BC} L_B$$=I_B L_B$となって$p$は$I_B$を通ります。残りは自力で確かめてください。

「放物線を描いたとて……」と逡巡する暇は与えません。$M_2$（線分$I_B I_C$の中点）と$K_A$は点$D$に関して対称な位置にありますから、$K_A M_2=2DM_2$が成り立ちます。至極当たり前に見えますが、実はこれを上手く活かせるのです。以下のような定理が有るからです。

（放物線の有名な性質）

　図で、$F$は放物線の焦点、$AB,AC$は接線である。このとき直線$AE$と準線は垂直であり、$D$は放物線上に存在する。さらに、$\triangle BFA \sim \triangle AFC$も成立する。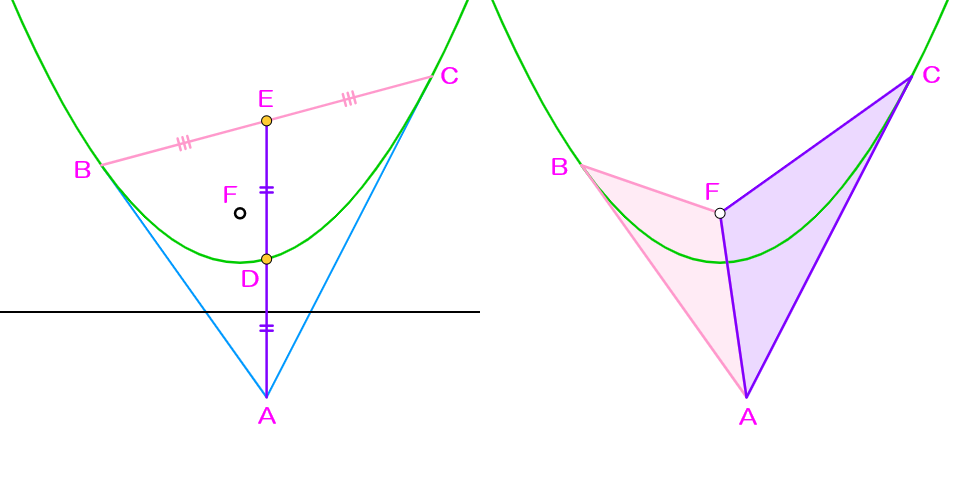

　定理4の証明はこちらのサイトを参照しましょう（決して怪しいサイトではありません）。「test2.pdf」や「test3.pdf」辺りに書いてあります。
　さて、定理4から、$K_A I_B,K_A I_C$は放物線$p$の接線といえますね（正確には定理4の逆を用いていますが、これも真であることは疑いようがありません）。すなわち$\triangle I_C EK_A \sim \triangle K_A EI_B$です。放物線の軸と平行に入射した光線は焦点に集まる（$\Rightarrow$$K_A I_B$は$\angle EI_B L_B$を二等分する）ので、$\triangle K_A EI_B \equiv \triangle K_A L_B I_B$も得られます。これらを図に描き込みましょう。

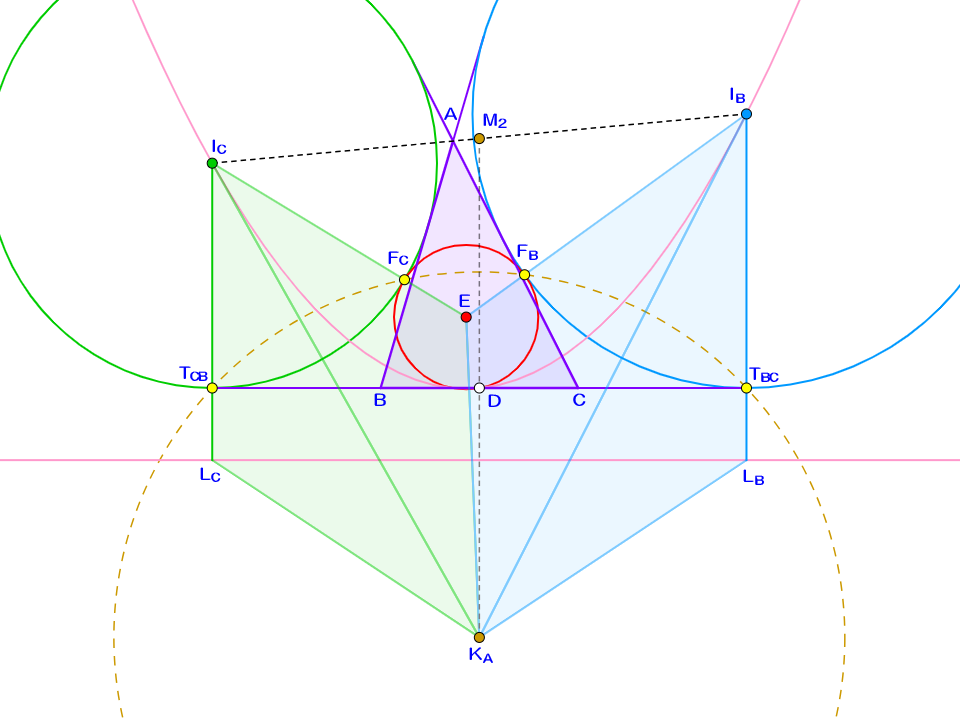
　もう見えていますね。$\triangle K_A EI_B$と$\triangle K_A L_B I_B$の合同において$F_B$と$T_{BC}$は対応する点ですから、もちろん$K_A F_B=K_A T_{BC}$です。来ました。ここでやっと補題3が使えて、$(W,W_2,$$Y,Y_2,$$T_{BC},T_{CB},$$F_B,F_C)$の8点共円を示せるのです！　残る$(T_{CA},T_{AC},$$F_C,F_A,$$Y,U),$$(T_{AB},T_{BA},$$F_A,F_B,$$U,W)$の組も同様の議論により共円と導けます。ついに問題2を証明できました。

〈2nd step〉

　ようやく〈2nd step〉が始まります。ここでは$X'=F_A$を示しましょう（他の一致も同様に示せます）。
　$F_A$に関する情報を増やすため、以下の補題を設けます。

　問題1における$I_A,\omega_A,U$の定義はそのまま用いる。$\triangle ABC$の$\angle A$内の外フォイエルバッハ点を$F_A$とし、$\omega_A$と辺$BC$の接点を$S_A$とする。点$I_A$に関して$S_A$と対称な点を${S'}_{\! A}$と名付けると、$F_A$は直線$U{S'}_{\! A}$上に存在する。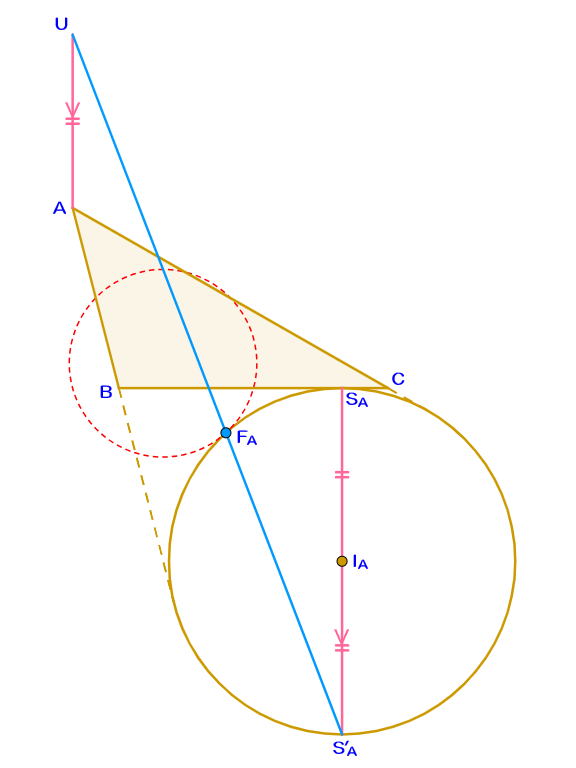

　$\angle A$が鋭角の場合のみ記す（直角・鈍角の場合も同様に示せる）。$\triangle ABC$の外心$O$について$M_2$（線分$I_B I_C$の中点）と対称な点を${M'}_{\! 2}$とすると、${M'}_{\! 2}$は$\triangle BCI_A$の外心になっている（有名性質）。線分$HM_2$の中点$M_H$について、九点円と外接円の相似に注目すれば、$M_H$は$\triangle ABC$の九点円に乗っており、かつ$BC \perp EM_H$であるといえる（ただし$H$は$\triangle ABC$の垂心）。いま、$\angle A$の二等分線と直線$EM_H$の交点を$F$とし、$AI_A$と$HM_2$の交点を$N_0$とする。$\triangle AHN_0$と$\triangle {M'}_{\! 2}M_2 N_0$の相似に注目すれば、$FM_H=\dfrac{\qty|AH-{M'}_{\! 2}M_2|}{2}$$=O{M'}_{\! 2}-OD=D{M'}_{\! 2}$が判り、特に$FM_H=D{M'}_{\! 2}$である。
　さて、$F_A$は明らかに$M_H {S'}_{\! A}$上の点であるため、$\angle A$の二等分線と直線$M_H {S'}_{\! A}$の交点を$M_U$とし、$\triangle M_H FM_U$と$\triangle {S'}_{\! A}I_A M_U$の相似を考えると、$\dfrac{FM_U}{M_U I_A}=\dfrac{FM_H}{I_A {S'}_{\! A}}$$=\dfrac{D{M'}_{\! 2}}{I_A S_A}$が従う。
　ところで、補題2の証明過程から3点$U,M_1,I_A$は共線であり（ただし$M_1$は線分$AS_A$の中点）、有名性質と併せれば$D$もこの直線に乗っている。ゆえに、$A$から$BC$に下ろした垂線の足を$H_A$、直線$BC$と直線$EM_H$の交点を$N_1$とすると、$\triangle I_A D{M'}_{\! 2}$と$\triangle I_A UA$の相似から$\dfrac{H_A D}{DS_A}=\dfrac{UA}{D{M'}_{\! 2}}-1$$=\dfrac{I_A S_A}{D{M'}_{\! 2}}-1$が判明する。したがって、
$$\begin{align} \dfrac{H_A N_1}{N_1 S_A} &=\dfrac{H_A N_1}{H_A D}\times\dfrac{H_A D}{D S_A}\times\dfrac{D S_A}{N_1 S_A} \\ &=\dfrac{1}{2}\times\dfrac{H_A D}{D S_A}\times\qty(\dfrac{D S_A}{\frac{1}{2}H_A D+D S_A}) \\ &=\dfrac{1}{2}\times\dfrac{H_A D}{D S_A}\times\qty(1+\dfrac{H_A D}{2 D S_A})^{-1} \\ &=\dfrac{H_A D}{D S_A}\times\qty(2+\dfrac{H_A D}{D S_A})^{-1}=\qty(1+\dfrac{2DS_A}{H_A D})^{-1} \\ &=\qty(1+2\qty(\dfrac{I_A S_A}{D{M'}_{\! 2}}-1)^{-1})^{-1}=\dfrac{I_A S_A-D{M'}_{\! 2}}{I_A S_A+D{M'}_{\! 2}} \end{align}$$
$$\dfrac{AF}{F I_A}=\dfrac{H_A N_1}{N_1 S_A}=\dfrac{I_A S_A-D{M'}_{\! 2}}{I_A S_A+D{M'}_{\! 2}}$$
$$\begin{align} \dfrac{AM_U}{M_U I_A} &=\dfrac{AF+FM_U}{FI_A-FM_U} \\ &=\dfrac{\frac{AF}{FI_A}+\frac{FM_U}{FI_A}}{1-\frac{FM_U}{FI_A}}=\dfrac{\frac{AF}{FI_A}+\frac{FM_U}{FM_U +M_U I_A}}{1-\frac{FM_U}{FM_U +M_U I_A}} \\ &=\dfrac{\frac{I_A S_A-D{M'}_{\! 2}}{I_A S_A+D{M'}_{\! 2}}+\frac{D{M'}_{\! 2}}{D{M'}_{\! 2}+I_A S_A}}{1-\frac{D{M'}_{\! 2}}{D{M'}_{\! 2}+I_A S_A}}=1 \end{align}$$
を導けて、$M_U$は線分$AI_A$の中点であるといえる。最後に$\triangle UAM_U$と$\triangle {S'}_{\! A}I_A M_U$を考えると、ここまでの議論からこれらは合同であり、$M_U$は線分$U{S'}_{\! A}$の中点にもなっている。$F_Aは$直線$M_U {S'}_{\! A}$上の点であったから、本補題の証明は既に完了している。$\blacksquare$

　補題5、かなり重かったですね。ティーブレイクとして、次は易しい補題を示します。

　ここまでに登場した$\omega_A,I_A,$$T_{AB},T_{AC},$$S_A,D$の定義はそのまま用いる。辺$AC$の中点を$M_3$、$C$から$AI_A$に下ろした垂線の足を$R_3$としたとき、$R_3$は直線$S_A T_{AB}, M_3 D$のいずれにも含まれる。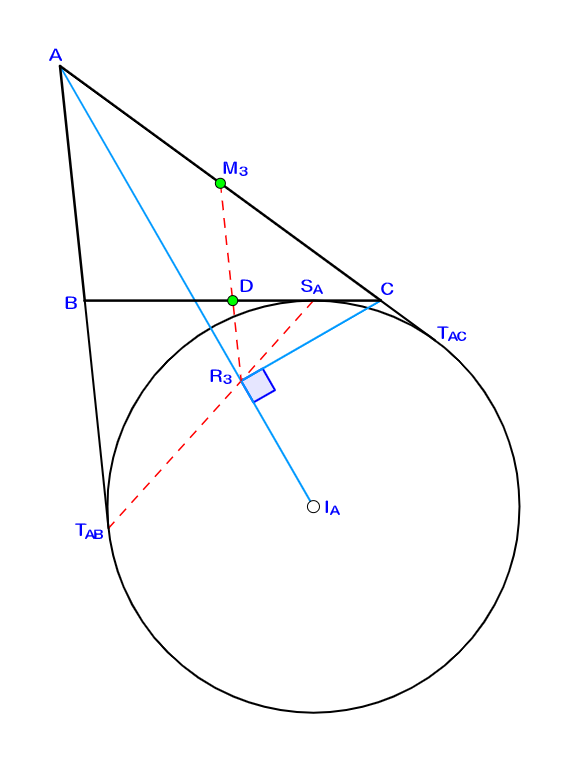

　まず簡単な計算から、$M_3$は$\triangle ACR_3$の外心である。ここから$\angle CM_3 R_3=2\angle CAR_3$$=\angle BAC$となり、$AB / \! / M_3 R_3$が判る。中点連結定理の逆より、$D$は$M_3 R_3$上の点であると示される。
　以上のことから、$M_3 R_3=\dfrac{1}{2}AC$も得られる。いま、$C$から引いた$AB$の平行線と直線$S_A T_{AB}$の交点を$G_3$とする。明らかに$\triangle S_A BT_{AB} \sim \triangle S_A CG_3$なので、$CG_3=CS_A$$(=CT_{AC})$となる。線分$T_{AB} G_3$の中点を${R'}_{\! 3}$とし、四辺形$AT_{AB}G_3 C$に注目すれば、$M_3 {R'}_{\! 3}=\dfrac{\qty|AT_{AB}-CG_3|}{2}$$=\dfrac{\qty|AT_{AC}-CT_{AC}|}{2}$$=\dfrac{1}{2}AC$と計算される。結局$R_3$と${R'}_{\! 3}$は一致し、これが本補題の示すべきことである。$\blacksquare$

　ついてきていますか？　難所と告知した以上、まだまだ続きますよ。ここからは、$I_A$を直線$T_{AB}T_{AC}$に関して対称移動させた点${I'}_{\! A}$が登場します。何となく問題1の影が見えてきたのではないでしょうか。
　また、外フォイエルバッハ点という扱いづらい点をどうにか他のものと結びつけるため、オイラー・ポンスレ点という大道具を持ち出します。

（オイラー・ポンスレ点）

　4点$(A,B,C,D)$を用意する。以下の8つの円をすべて定義できて、かつ少なくとも2円が相異なるとき、これらの円は共通する1点（オイラー・ポンスレ点）を通る。
・$\triangle ABC,$$\triangle BCD,$$\triangle CDA,$$\triangle DAB$の九点円。
・$\triangle ABC,$$\triangle BCD,$$\triangle CDA,$$\triangle DAB$の$D,A,B,C$における垂足円。

　恐ろしい定理ですね。ちなみに、証明や使用法は denta_geometry氏のMathlog記事で確認できます。
　さて、もとの問題で4点$(A,B,C,I_A)$のオイラー・ポンスレ点$E_P$を考えましょう。$E_P$は$I_A$における$\triangle ABC$の垂足円上にあります。この円は明らかに傍接円$\omega_A$と一致しますね。また、$E_P$は$\triangle ABC$の九点円にも乗っているようです。もうお分かりですね、つまり$E_P=F_A$です。要するに、$\triangle ABC,$$\triangle BCI_A,$$\triangle CI_A A,$$\triangle I_A AB$の九点円、および$\triangle ABC,$$\triangle BCI_A,$$\triangle CI_A A,$$\triangle I_A AB$の$I_A,A,B,C$における垂足円はすべて$F_A$を通ります。恐ろしい定理ですね（2回目）。

　さて、上記を踏まえ、以下の補題に挑みます。（注：$\triangle ABC$が二等辺三角形の場合は補題8が成立しない(円が直線に退化する)ため、個別に考える必要があります。ただ二等辺三角形であれば問題1を速攻で解けるので、この議論はカットしましょう。）

　ここまでに登場した$F_A,I_A,{I'}_{\! A},{S'}_{\! A}$の定義はそのまま用いる。4点$(F_A,I_A,{I'}_{\! A},{S'}_{\! A})$は共円である。

　$B,C$から直線$AI_A$に下ろした垂線の足を$B_A,C_A$とし、$AI_A$と$T_{AB}T_{AC}$の交点を$M_4$とする。$\triangle ACI_A$の九点円$n_4$を考えると、$M_U$（線分$AI_A$の中点）、$C_A$および$T_{AC}$は明らかに$n_4$上の点である。オイラー・ポンスレ点となる$F_A$も、当然$n_4$に乗っている。この円を$\omega_A$で反転させた円${n'}_{\! 4}$が、どのような点を通るか考えよう。
補題6より、直線$S_A T_{AC},S_A T_{AB}$はそれぞれ$B_A,C_A$を通る。$B$から引いた$\omega_A$の極線こそが$S_A T_{AB}$であるから、$C_A$から引いた$\omega_A$の極線は$B$を通り$AI_A$に垂直な直線である。この極線はすなわち直線$BB_A$であり、ゆえに$B_A$と$C_A$は$\omega_A$に関する反転で互いに移りあう。また、$A$と$M_4$も$\omega_A$に関する反転で互いに移りあう点の組であるから、$I_A {I'}_{\! A}\times I_A M_U=2I_A M_4 \times \dfrac{I_A A}{2}$$=(\textrm{radius of}\;\omega_A)^2$となり、${I'}_{\! A}$と$M_U$も$\omega_A$に関する反転で互いに移りあう。
　したがって、${n'}_{\! 4}$が通る点として、${I'}_{\! A}$（$M_U$の反転先）、$B_A$（$C_A$の反転先）、$T_{AC}$および$F_A$の4点が挙げられる。ゆえに4点$({I'}_{\! A},B_A,T_{AC},F_A)$は共円といえる。
　あとは円周角の定理を用いればよい（ここでは四角形$F_A {I'}_{\! A}I_A {S'}_{\! A}$が凸四角形となる場合を考えているが、代わりに四角形${I'}_{\! A}F_A I_A {S'}_{\! A}$が凸四角形となる場合もほぼ同様に証明できる）。$\angle B_A {I'}_{\! A} F_A=\angle B_A T_{AC} F_A$$=\angle S_A T_{AC} F_A$$=\angle S_A {S'}_{\! A} F_A$と追跡することで、四角形$F_A {I'}_{\! A}I_A {S'}_{\! A}$は円に内接すると断言できる。$\blacksquare$

　途中で極線周りの議論をしたので、振り落とされた読者がいらっしゃるかもしれません。必要ならば、 Metachick_XOR氏のMathlog記事で復習しましょう。

　さあ、これで〈2nd step〉関連の補題はすべて示しました。図のように、$\triangle I_A BC,$$\triangle I_A CA,$$\triangle I_A AB$の外心$O_A,O_B,O_C$をとりましょう。

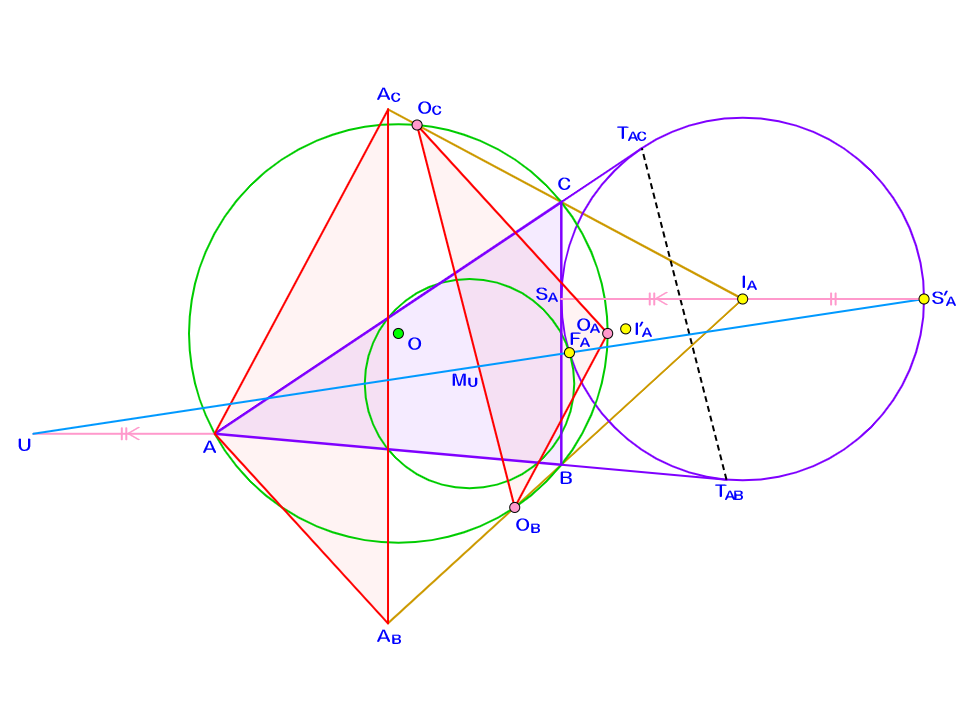
　有名性質から、$O_B$は$\triangle ABC$の外接円上にあり、また直線$I_A B$にも乗っています（$O_A,O_C$も同様）。$O_B A=O_B I_A$および$O_C A=O_C I_A$なので、$O_B O_C$は線分$AI_A$の垂直二等分線であり、すなわち$M_U$を通るのですね。同様に考えれば、$O_A O_B \perp CI_A,$$O_C O_A \perp BI_A$を示せます。つまり$I_A$は$\triangle O_A O_B O_C$の垂心です。
　このタイミングで、$A$から直線$I_A B,I_A C$へ垂線を下ろし、その足を$A_B,A_C$とおきましょう。すると、四角形$AA_B I_A A_C$は円に内接し、その円の中心は$M_U$です。よって、$\angle AA_B A_C=\angle AI_A A_C$$=\angle O_A I_A O_C$$=\angle O_A O_B O_C$が成り立ち、同様に$\angle AA_C A_B=\angle O_A O_C O_B$も判ります。ここから$\triangle AA_B A_C \sim \triangle O_A O_B O_C$が得られるのです。

　さて、補題6より、直線$A_B A_C$は辺$AB,AC$の中点を通ります。ゆえにこの直線は$M_1$（線分$AS_A$の中点）も通っており、3点$(I_A,D,M_1)$の共線から$A_B M_1=A_C M_1$も明らかです。補題2の結果と併せると、点$M_1$が線分$UI_A$および線分$A_B A_C$の中点であることが判るので、四角形$UA_B I_A A_C$は平行四辺形といえますね。特に$AA_B \perp A_B I_A / \! / UA_C,$$AA_C \perp A_C I_A / \! / UA_B$となり、$U$は$\triangle AA_B A_C$の垂心です。
　したがって、$\triangle AA_B A_C$と$\triangle O_A O_B O_C$の相似において、外心→垂心→対応する頂点、の順で点を結ぶ操作を考えれば、$\angle M_U UA=\angle OI_A O_A$が判明します。これと補題5、補題8を適宜用いることにより、$\angle F_A {I'}_{\! A} O_A=\angle F_A {S'}_{\! A} I_A$$=\angle U {S'}_{\! A} I_A$$=\angle {S'}_{\! A} UA$$=\angle M_U UA=\angle OI_A O_A$と角度追跡が可能です。最左辺と最右辺だけ取り出すと、$\angle F_A {I'}_{\! A} O_A=\angle OI_A O_A$が得られています。ということは、直線$F_A {I'}_{\! A}, OI_A$の交点を$J$とおけば、$\triangle JI_A{I'}_{\! A}$は$JI_A=J{I'}_{\! A}$の二等辺三角形なのですね。結局$J$は直線$T_{AB}T_{AC}$上に存在し、ゆえに$F_A$を直線$T_{AB}T_{AC}$に関して対称移動させた点${F'}_{\! A}$は直線$OI_A$に乗るといえます。

　最後の角度追跡です。$\angle T_{AB}{F'}_{\! A}T_{AC}=\angle T_{AB}F_A T_{AC}$$=\angle T_{AB}S_A T_{AC}$$=\angle BIC$と追っていくと（ただし$I$は$\triangle ABC$の内心）、${F'}_{\! A}$は直線$OI_A$上の点であり、$\angle T_{AB}{F'}_{\! A}T_{AC}=\angle BIC$をみたす、といえます。……これだけ語れば察しがつきますね、つまり${F'}_{\! A}=X$です！　この結論から、自明に$X'=F_A$を主張できます。同様に$Z'=F_B,$$V'=F_C$を証明できるので、ついに、ついに〈2nd step〉が終わりました。

〈3rd step〉

　長い長い議論の果てに、いよいよ$\dfrac{UV \times WX \times YZ}{VW \times XY \times ZU}$を考えるときがきました。〈2nd step〉で示した事実より、
$$\begin{align} \dfrac{UV \times WX \times YZ}{VW \times XY \times ZU} &=\dfrac{UV' \times WX' \times YZ'}{V'W \times X'Y \times Z'U} \\ &=\dfrac{UF_C \times WF_A \times YF_B}{F_C W \times F_A Y \times F_B U} \end{align}$$です。一方、〈1st step〉で示した問題2によれば、$(F_C,F_A,$$Y,U),$$(F_A,F_B,$$U,W),$$(F_B,F_C,$$W,Y)$は共円でした。もとの図からここだけを取り出します。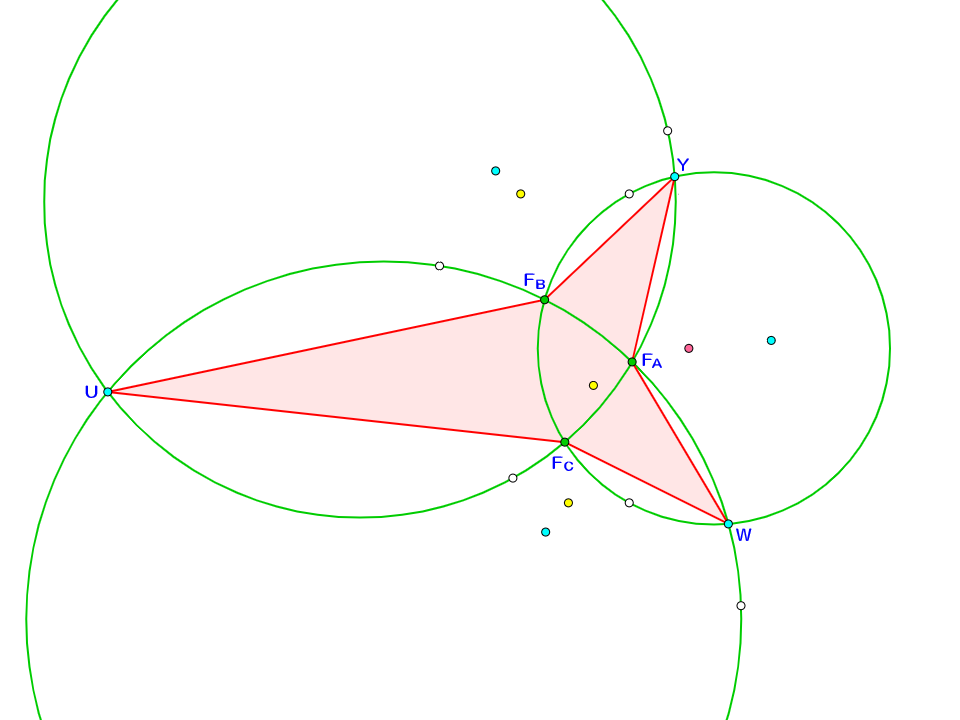

「……あれ？　もう終わり？」
　お気づきですね、〈3rd step〉はこれで終わりです。最序盤で言及した春木の定理を適用し、$\dfrac{UF_C \times WF_A \times YF_B}{F_C W \times F_A Y \times F_B U}=1$と計算できますね。わざわざstepを設けるまでもありません。ともかく我々は、とうとう$\dfrac{UV \times WX \times YZ}{VW \times XY \times ZU}=1$を完全に論証できたのです。

解答発表

$1$

〈2024/05/23追記〉なお、ここまでに用いた補助線を1つの図にすべて描き込むと、以下の画像のようになります。~~なぜ解けると思った？~~

余興の季

　〈2nd step〉の補題8に再度注目します。${S'}_{\! A}$を直線$T_{AB} T_{AC}$に関して対称移動させた点${S''}_{\! A}$を考えれば、${S''}_{\! A}$は$(F_A,I_A,$${I'}_{\! A},{S'}_{\! A})$の乗っていた円と同じ円上にありますね（$\because$ この円の中心は$T_{AB} T_{AC}$上にある）。また、${I'}_{\! A} {S''}_{\! A}=I_A {S'}_{\! A}$$=I_A F_A$より、四角形$F_A {S''}_{\! A} I_A {I'}_{\! A}$（あるいは四角形$F_A I_A {S''}_{\! A} {I'}_{\! A}$）は$F_A {I'}_{\! A} / \! / I_A {S''}_{\! A}$の等脚台形と言えるのです。
　いま、直線$F_A {I'}_{\! A}$を直線$T_{AB} T_{AC}$に関して対称移動させると直線$O I_A$に一致しました（〈2nd step〉の主結果）。ゆえに、直線$I_A {S''}_{\! A}$を直線$T_{AB} T_{AC}$に関して対称移動させた直線、すなわち直線${I'}_{\! A} {S'}_{\! A}$は、直線$OI_A$と平行になるのです。$\triangle ABC$の内接円$\omega$と辺$BC,CA,AB$の接点$S_a,S_b,S_c$、および$I$を直線$S_b S_c$で対称移動させた点$I'$について、$\omega_A$が$\omega$に移るような点$A$中心の相似拡大を考えれば、$S_a I' / \! / OI_A$が成立することになります。

　ここに yuu氏のMathlog記事の補題4を重ねることで、同記事のメインでもある、以下の有名な定理が証明できます。当該補題を認めればほとんど自明なので、厳密な証明は割愛します。

　$\triangle ABC$の外心・内心・$\angle A$内の傍心をそれぞれ$O,I,I_A$とし、直線$BI$と辺$AC$の交点を$E$、直線$CI$と辺$AB$の交点を$F$とおく。このとき、$EF \perp OI_A$が成立する。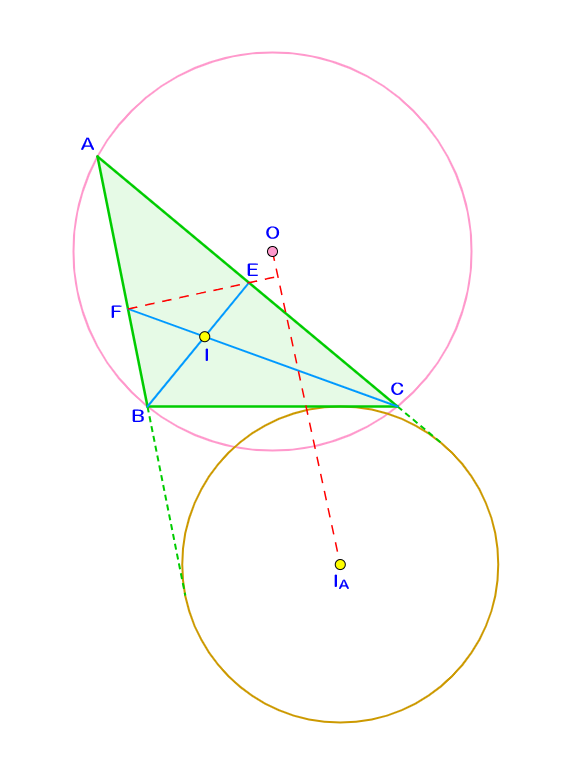

　各所で難問扱いされているこの定理も、問題Ｆという怪物の前には単なる余興でしかなかったのですね。

あとがき

　激重でしたね。外フォイエルバッハ点、補助放物線、8点共円、オイラー・ポンスレ点に春木の定理……。先日開催された IMO2023の第6問に高難度の幾何が入っていたと一部で騒がれましたが、少なくともアレの3倍は難しいと自認しています。HTMLコード（タグ含む）は無事に25,000文字を超えました。問題Ａ～問題Ｅの解説記事と併せれば、実に約43,000字、約69,000Byte（UTF-8）ものコード長です。こんなものを開催期間5日のコンテストで解かせようとした主催者がいるとは考えられません。ねえ、主催者さん？
　余談ですが、〈2nd step〉のために元々用意していた証明はさらに長く煩雑なものでした。コンテスト期間直前に先行研究を漁ったところ、こちらの論文に素晴らしいアイデアが載っていたため、そのアイデアを応用した比較的簡潔な証明（簡潔とは言っていない）に差し替えた次第です。

　各問題の作問背景や主催者なりの感想を述べて締めましょう。まず問題Ａ。こちらは天真様による作問であり、3月末に提供していただきました。自作ではないので上手く語れませんが、コンテストの「入り口」として、非常に相応しい問題であったと考えます。この「入り口」のおかげで、今回のエスパー杯は歴代最多の参加者数を達成できました。ありがたやありがたや。
　続いて問題Ｂ。有名な性質を活かした、翔子さん様による作問です。翔子さん様（敬称の重複？）は色々な場で数多の作問に携わっているそうで、本問も参加者の「解きたいという欲求」を刺激する良問となっていました。こういう低難易度幾何の作り方、どこかに載っていないものでしょうか？　どうでもよい情報として、主催者はコンテスト終了後に「フィンスラー・ハドヴィッガーの定理」という名称を知りました。
　ここから主催者の自画自賛になるのですが、問題Ｃ。元々はＤとＥの中間くらいの難易度で進む幾何研究から生まれたものです。数学オリンピック頻出のこの構図を知っていれば、決して難しくなかったでしょう。強いて申し上げれば外角の二等分線を見つける部分？　……意外と語ることがありませんね。
　問題Ｄ。主催者的には良問のつもりで出しましたが、そもそも挑戦者自体が少なかったです……難しくないのに……。こういう非典型的な求積問題は第３回の問題Ｂを彷彿させますね。求めやすい面積から等積を追うことで、正解に辿り着くタイプの問題です。先述の翔子さん様からDMにて「問題Ｄがめっちゃ好きです！！！」と告白されたことを誇りに、栄えある余生を過ごすこととします。
　難易度が急上昇して、問題Ｅ。第３回のラスボスとして華々しく登場したオリジナル定理、「レムニスケート版『余弦定理』」を、さらに応用させたものです（なぜ？）。2024年現在、レムニスケートアレルギーの有病率が著明な高値を呈しており、レムニスケートと遭遇するや否や重度のアナフィラキシーショックをきたす人々の脱感作に少しでも貢献できれば……と意図していたものの、どうやら禁忌肢を踏んだようです。申し訳ございません。アドレナリンは各自で調達してください。
　ラスト、駄目押しとしか形容できない問題Ｆ。求値として出題したため、正解率自体は高かったです。しかしながら、論証まで完遂した参加者は皆無でした。当たり前ですが、これは参加者の幾何力を侮った発言ではありません。ただ主催者がやりすぎただけです。せめて〈1st step〉で留めていれば難なく完答する方も出てきたかと思われます。仮に私が参加者としてこの問題と邂逅していれば、それはそれは清く虚しい椅子温めマシンが誕生していたことでしょう……。外心と傍心を結んだ時点で超難問と相場が決まっているのです（極論）。