第4回匿式図形問題エスパー杯 (T-GUESS Cup 4) 問題A~Eの解説
2024年5月3日~5月8日にかけて『
第4回匿式図形問題エスパー杯
(T-GUESS Cup 4: Tock's Geometry "Using Extra-Sensory Solutions" Cup The 4th)』を開催しました。ご参加くださった皆様、ありがとうございました。
本記事では、当該コンテストで出題した問題A・問題B・問題C・問題D・問題Eの紹介および解説を行います。最終問題である問題Fは話せば長くなるので別記事に……。
問題紹介
$\triangle ABC$において、辺$BC$の中点を$M$とし、辺$AB$上に$BD=BM$となる点$D$をとると、$AD=MD=10,$$AC \perp AM$が成立していた。このとき、線分$BM$の長さを求めなさい。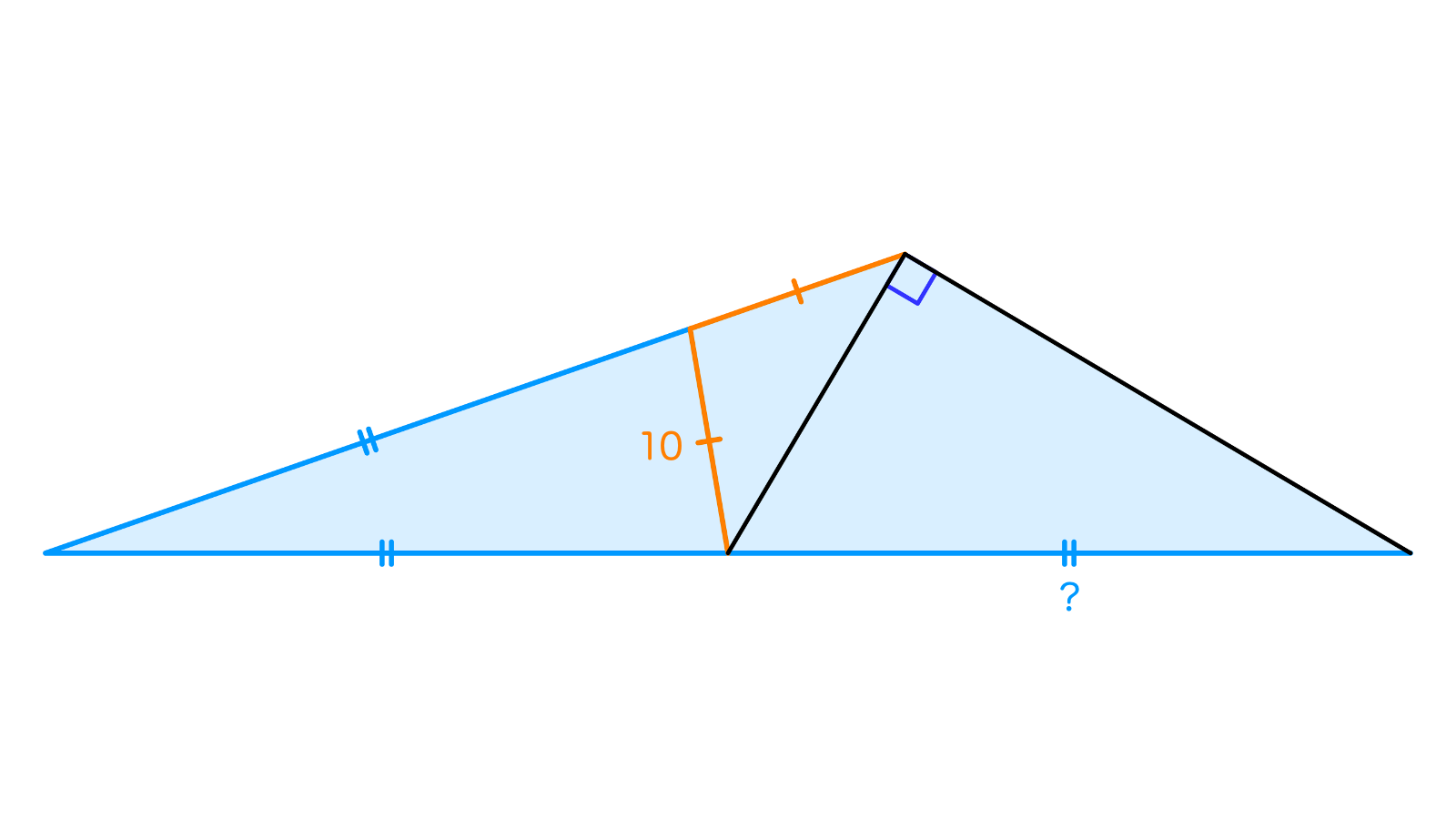
$\triangle ABC$の外側に2つの正方形$ABDE,ACFG$を描き、線分$BC,EG$の中点をそれぞれ$M,N$としたところ、$MN=6$となった。このとき、四角形$MDNF$の面積を求めなさい。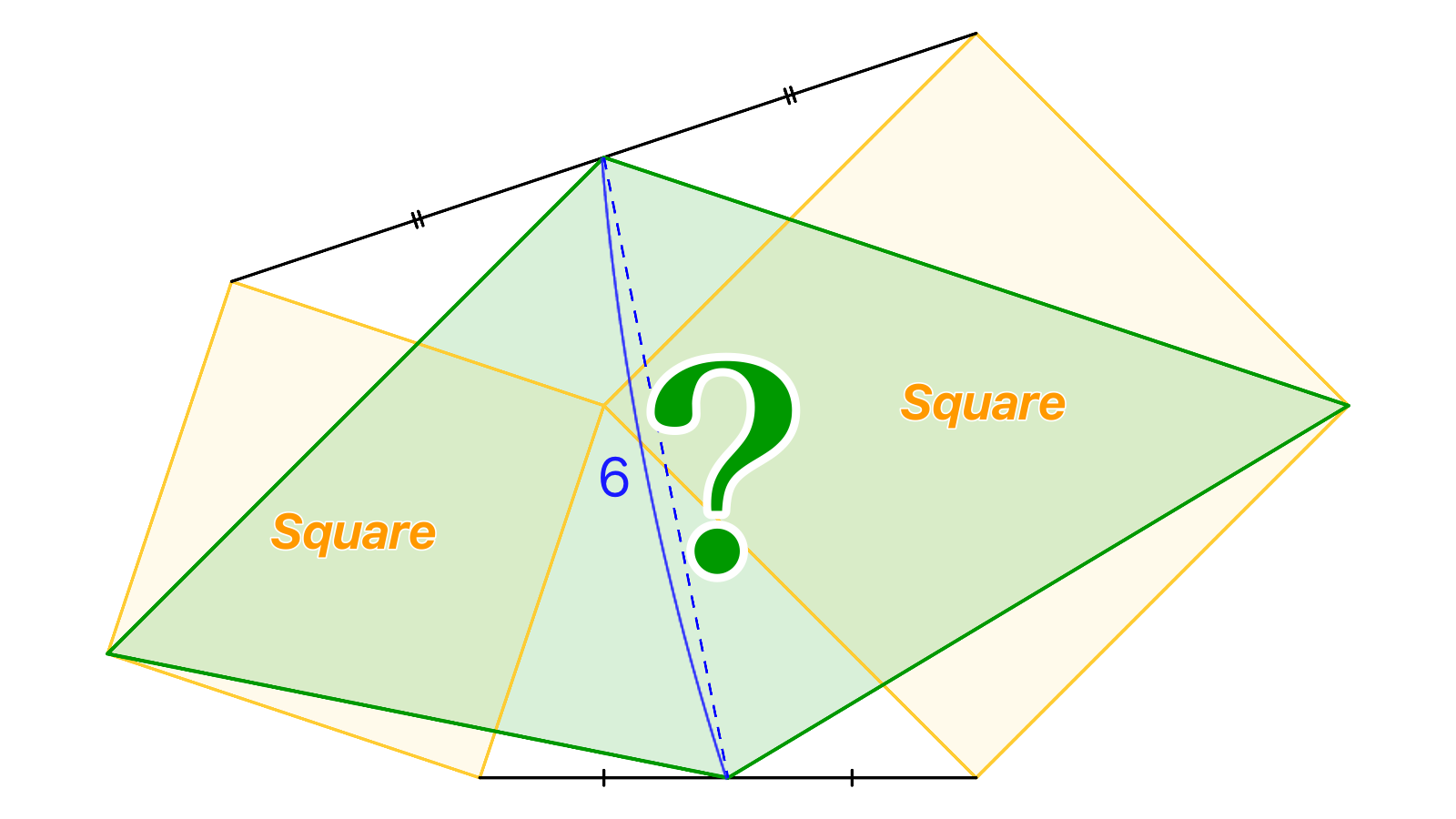
3点$(O,P,R),$$(O,Q,S)$はこの順に同一直線上にあり、$OP=OQ,$$OR=OS$をみたしている。2点$P,Q$でこれらの直線に接する円を$\Gamma_1$、2点$R,S$でこれらの直線に接する円を$\Gamma_2$とし、$\Gamma_1$と$\Gamma_2$の共通内接線(のひとつ)は$\Gamma_1,\Gamma_2$とそれぞれ$X,Y$で接しているとする。半直線$OX$と$\Gamma_2$の交点のうち、点$O$から遠いほうを$K$と名づけ、線分$XK$上に$OX=LK$となる点$L$をとる。
線分$XY$の中点$M$が$\angle OMX=\angle LMX$をみたし、かつ$OP=2$であるとき、線分$PR$の長さを求めなさい。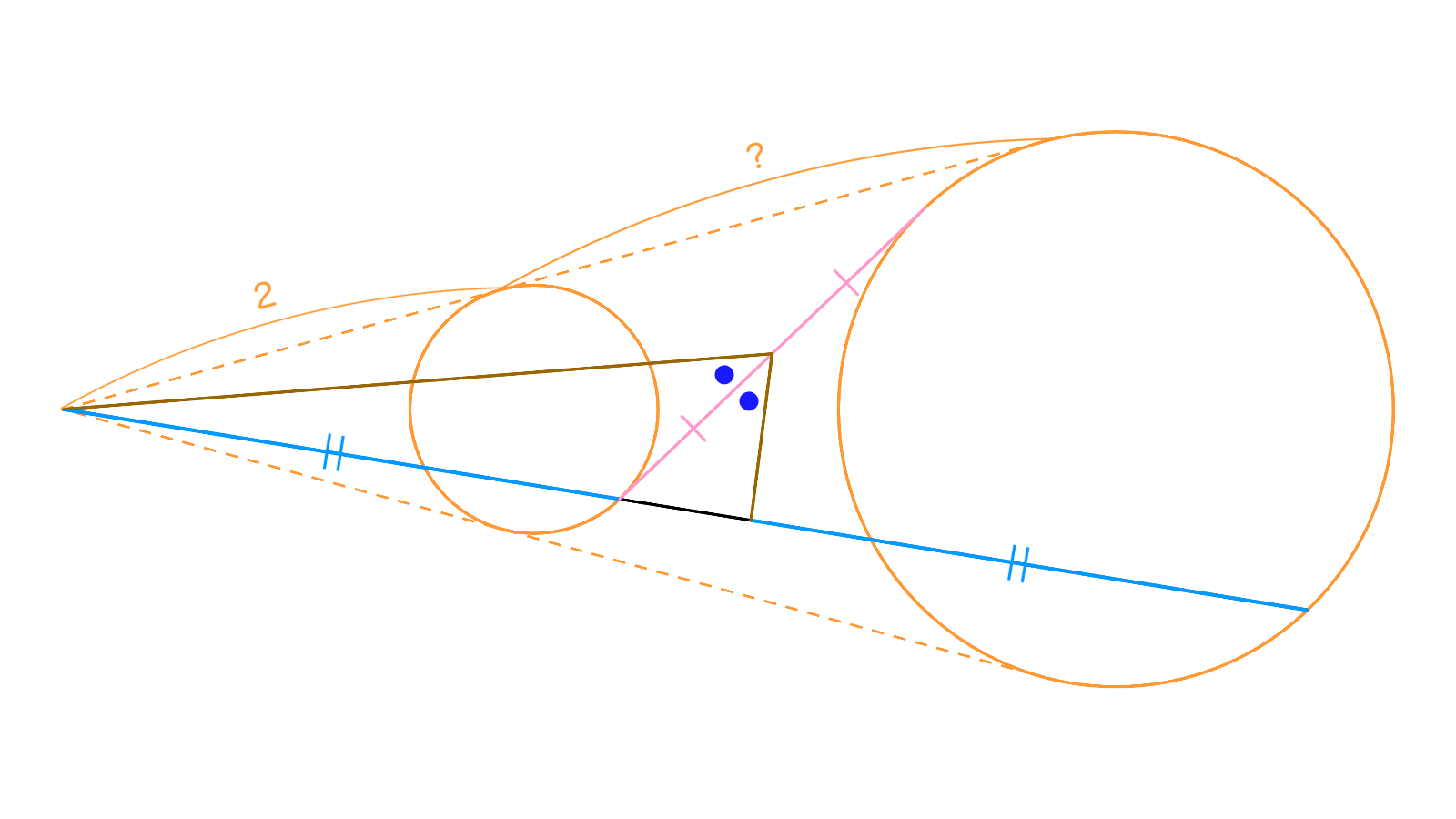
扇形$O_1 \overset{\Huge \frown}{AB}$の弧$AB$上に点$O_2$をとり、扇形$O_2 \overset{\Huge \frown}{CD}$を描くと、$\overset{\Huge \frown}{AB},\overset{\Huge \frown}{CD}$はそれぞれ$C,O_1$を通っており、扇形$O_2 \overset{\Huge \frown}{CD}$の中心角は${90}^{\circ}$であった。線分$AB$と$\overset{\Huge \frown}{CD},DO_2$の交点をそれぞれ$E,F$とすると、$E$はただ1点に定まり、図形$\overset{\Huge \frown}{ED}F,\overset{\Huge \frown}{CE}FO_2$の面積はそれぞれ$7,9$であった。
$\triangle ACE$の外接円が線分$CO_1,AO_2$の交点$G$を通るとき、図形$F\overset{\Huge \frown}{BO_2}$の面積はいくらか。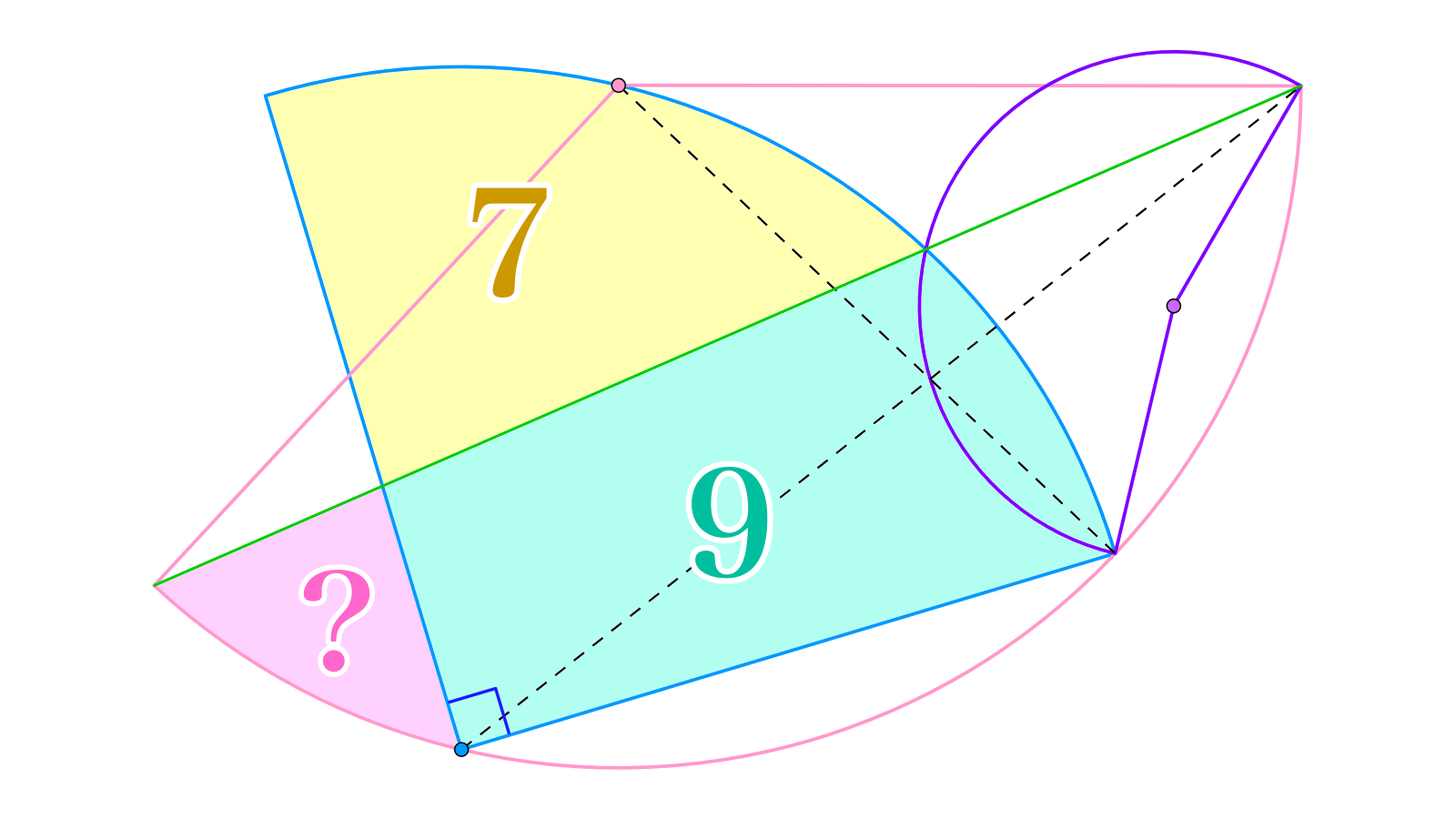
円$\Gamma$上に4点$A,B,C,F_1$が存在し、$\triangle ABC$は1辺の長さが$1$の正三角形である。$F_1$を$C$に関して対称移動させた点${F'}_{\! 1}$について、2点$F_1,{F'}_{\! 1}$を焦点にもつレムニスケート$\lambda_1$は$\Gamma$と$C$でない2点$X,Y$で交わっており、$B{F'}_{\! 1}=2$である。
このとき、$B$を中心とし2点$X,Y$を通るレムニスケート$\lambda_2$と、$A$を中心とし2点$X,Y$を通るレムニスケート$\lambda_3$の面積比はいくらか。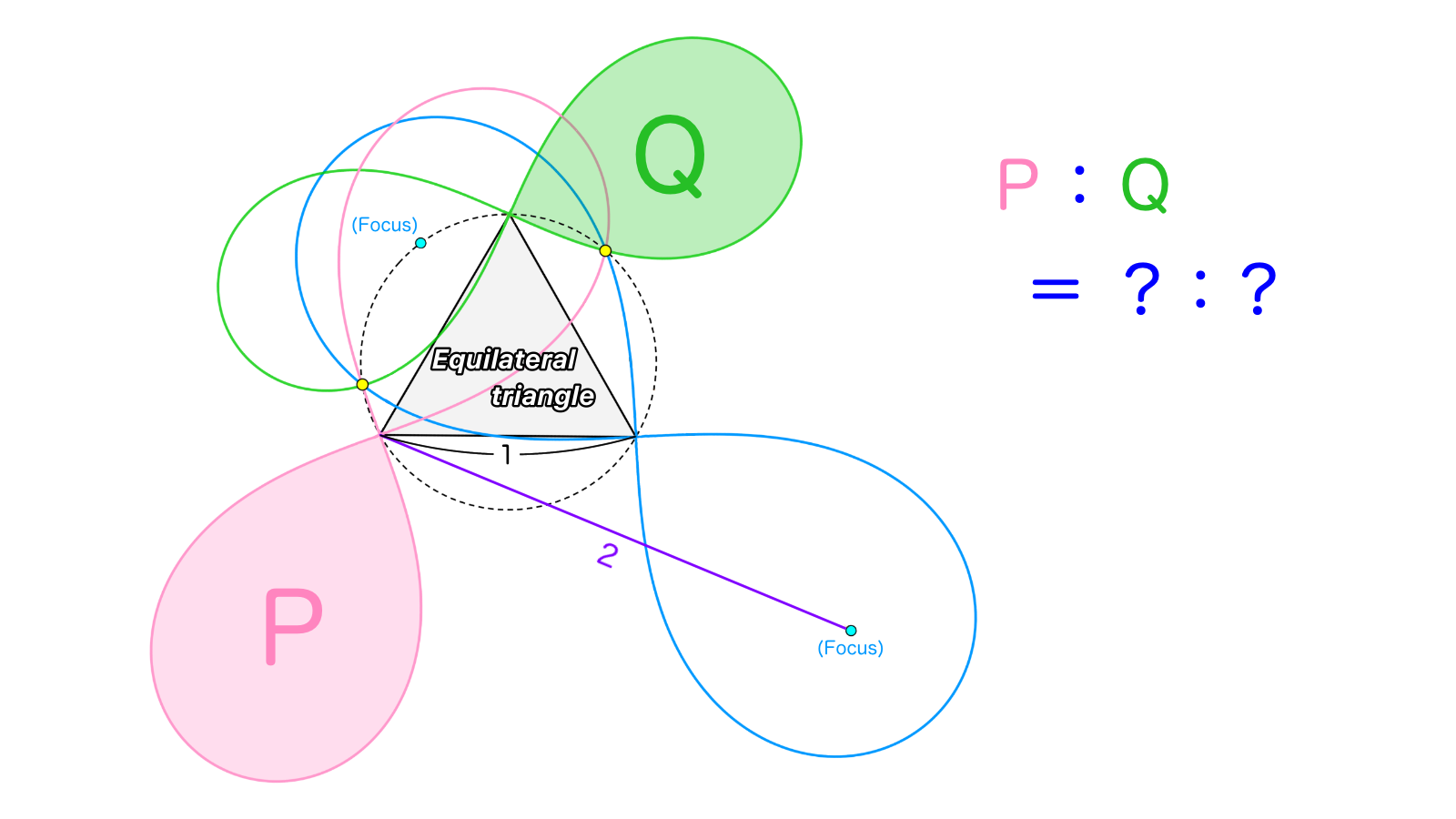
解答発表
問題A $30$
問題B $36$
問題C $2\sqrt{5}-2$
問題D $\dfrac{5}{3}$
問題E $\sqrt{157}:2\sqrt{19}$
軽い解説
問題A
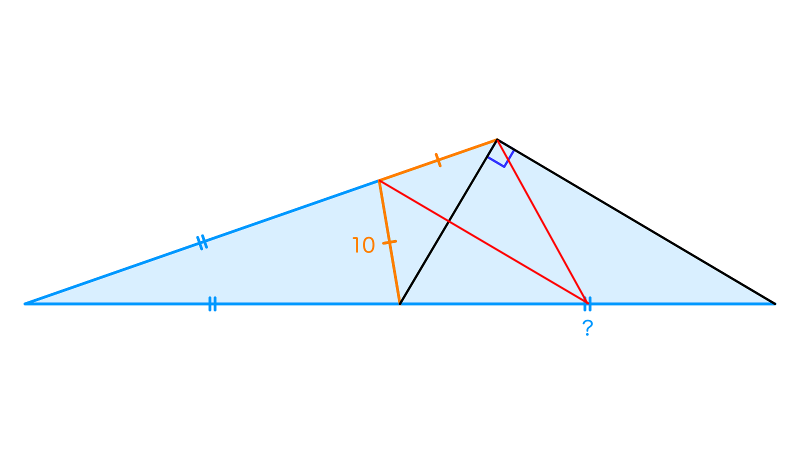
線分$CM$の中点を$N$とすると、円周角の定理の逆から$N$は$\triangle AMC$の外心になっています。つまり$AN=MN$ですから、直線$DN$は線分$AM$の垂直二等分線ということになりますね。$AC \perp AM$より$AC / \! / DN$が得られ、したがって$\dfrac{BD}{DA}=\dfrac{BN}{NC}$$=3$です。ここに$AD=10$を代入すれば$BM=30$が確定します。
問題B
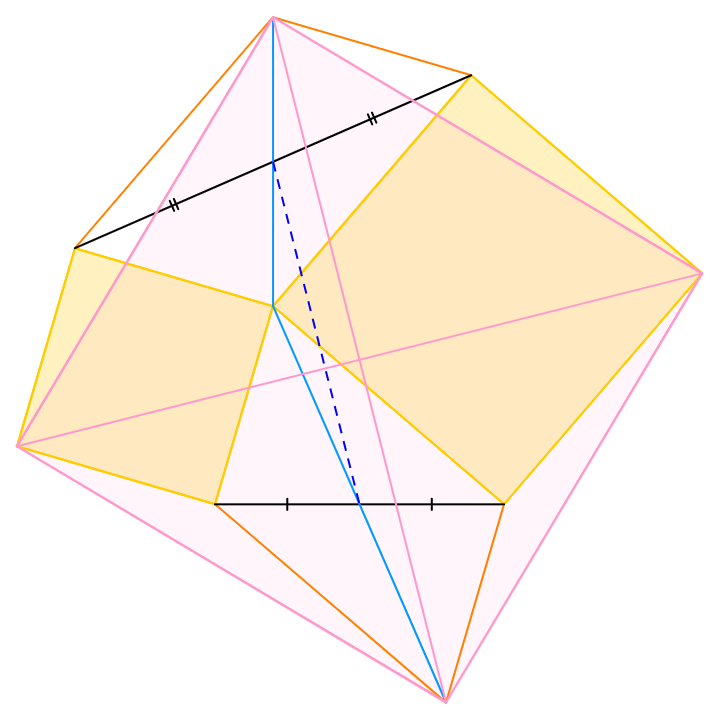
点$M$、点$N$に関して$A$を対称移動させた点をそれぞれ$A_M,A_N$としましょう。対角線が各々の中点で交わるため、四角形$ABA_M C,AEA_N G$はともに平行四辺形です。
$\triangle DBA_M$と$\triangle A_M CF$において、$DB=AB=CA_M,$$BA_M=AC=CF$であり、
$$\begin{align} \angle DBA_M
&={360}^{\circ}-\angle DBA-\angle ABA_M \\
&={360}^{\circ}-\angle ACF-\angle A_M CA \\
&=\angle A_M CF \end{align}$$
も確かめられます。ゆえに$\triangle DBA_M$と$\triangle A_M CF$は合同です。同様にして$\triangle DBA_M \equiv \triangle A_M CF$$\equiv \triangle DEA_N$$\equiv \triangle A_N GF$が判り、結局四角形$A_M D A_N F$は正方形と示せます。
中点連結定理から$DF=A_M A_N=2MN,$$DF \perp A_M A_N / \! / MN$なので、求める面積は$\dfrac{MN \times DF}{2}={MN}^2=36$です。なお、
フィンスラー・ハドヴィッガーの定理
を知っていれば10秒もかからずに解答できます。
問題C
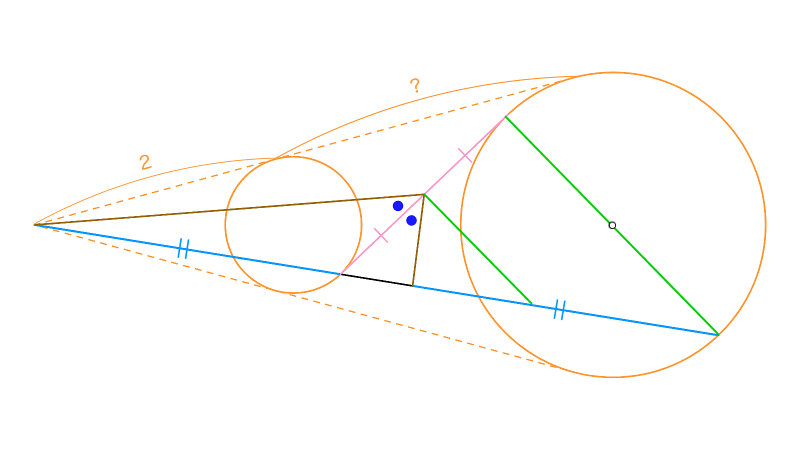
$O$に関する相似拡大を考えれば、$K$における$\Gamma_2$の接線は$XY$と平行であるといえます。つまり線分$YK$は$\Gamma_2$の直径となり、$\angle XYK={90}^{\circ}$です。また、線分$XK$の中点を$N$とすれば、$MX \perp MN$が簡単に分かります。これは直線$MN$が$\angle OML$の外角の二等分線になることを示しているので、
$$\begin{align} OX:XL &= ON:NL \\
&= \qty(OX+\dfrac{XL+LK}{2}):\qty(\dfrac{XL+LK}{2}-XL) \\
&= \qty(3OX+XL):\qty(OX-XL) \end{align}$$
という関係が成り立ちます。整理すれば、$\dfrac{XL}{OX}$についての2次方程式$\qty(\dfrac{XL}{OX})^2+4\qty(\dfrac{XL}{OX})-1=0$が出てきて、ここから$\dfrac{XL}{OX}=\sqrt{5}-2$が判明するのです($\because \dfrac{XL}{OX}>0$)。すなわち$PR=OP\times\dfrac{XK}{OX}$$=2\times\qty(\dfrac{XL}{OX}+1)$$=2\sqrt{5}-2$と求められます。この辺りから少し難易度が上がりましたね。
問題D
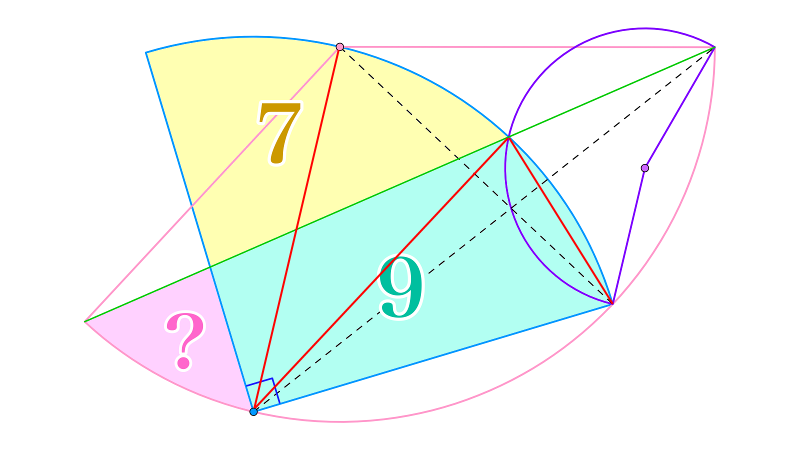
まずは丁寧に円周角を追っていきましょう。$\angle BO_1 O_2=2\angle BAO_2$$=2\angle EAG$$=2\angle ECG$$=2\angle ECO_1$$=\angle EO_2 O_1$と追跡できるので、$BO_1 / \! / O_2 E$が判ります。いま、線分$BO_1,O_2 E$の長さはどちらも線分$O_1 O_2$の長さと等しいので、四角形$BO_1 EO_2$は平行四辺形です。すなわち、この平行四辺形の中心$P$(線分$BE$と線分$O_1 O_2$の交点ですね)について、図形$P\overset{\Huge \frown}{BO_2}$と図形$P\overset{\Huge \frown}{EO_1}$が合同になります。
求める面積(図形$F\overset{\Huge \frown}{BO_2}$の面積)を$x$とおくと、上記の合同より、扇形$O_2 \overset{\Huge \frown}{CO_1}$の面積は$x+9$です。この扇形の中心角が${60}^{\circ}$であることは明らかなので、$(7+9)\times\dfrac{2}{3}$$=x+9$を解いて$x=\dfrac{5}{3}$を得ます。平行に気づけるかどうかがカギでした。
さて、コンテスト主催者の身ながら申し上げますが、ここまでは良かったのですよ。ここまでは。
参加者の大半を寄せつけなかった問題E・問題F。問題Eの時点で、主催者の想定難易度はT-GUESS Cup 2の
ラスボス
と同等でした。まさに非人道的といえますね(
出典
)。
取り敢えず大問題児の問題Fは放置し、問題Eだけでも解きましょう。
問題E
レムニスケート。よく知られた4次曲線です。はじめは手も足も出ないと思われるので、メタ的視点で攻めます。主催者かつ本問のwriterである 匿(Tock) が、過去に何かレムニスケートへの言及をしていないか、色々と探してみましょう。
圧倒的ですね。言及しまくっています。中でも、レムニスケートに関する 最新のMathlog記事 を開けば、以下のオリジナル定理が掲載されています。
$AB=x, AD=y$である平行四辺形$ABCD$の中心を$O$とし、2点$A,C$が焦点となるレムニスケートを$L_1$、2点$B,D$が焦点となるレムニスケートを$L_2$と定める。
いま、$L_1$上に$O$でない点$P$をとると、$O$を通り$P$で$L_1$に接する円が、$L_2$と$O$でない2点$X,Y$で交わった。このとき、$P$を中心とし2点$X,Y$を通るレムニスケート$L_3$について、$L_3$の面積は$2xy$である。
この定理が問題Eに効くことは自明でしょう。要するに本問は、コンテストという大義名分を得たただのオリジナル定理の宣伝ですね(おい)。私の定理にはこんな使い方があるよ、という。悪問では?
気を取り直し、問題を考えます。定理1を使いたいので、以下のように補助レムニスケート$\lambda_4$を描いてみます(しばらく使わないので$\lambda_2$は省略します)。
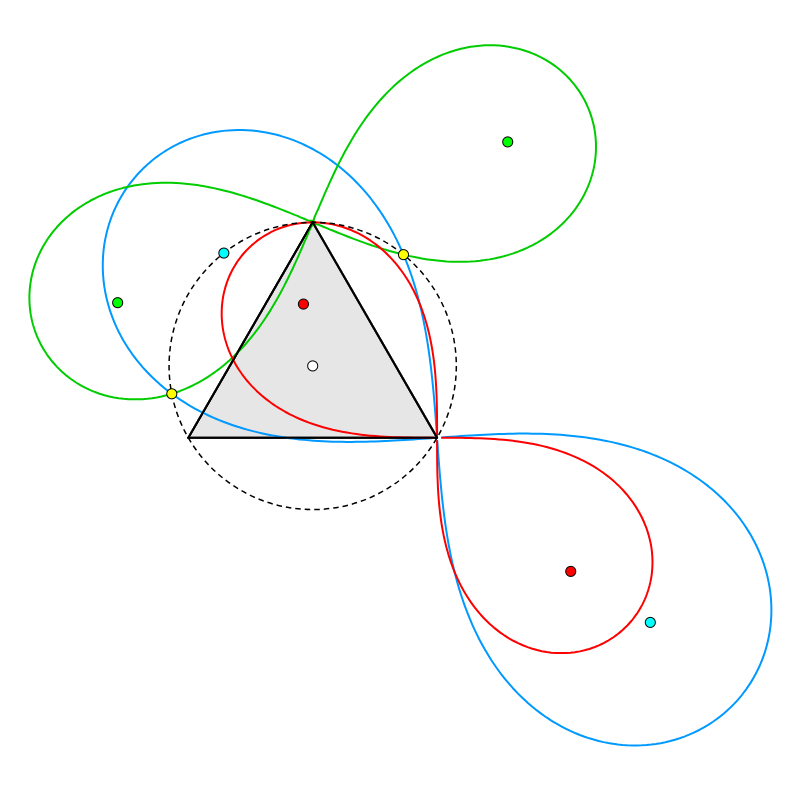
「は?????」
画面の向こうからそんな声が聞こえてきた気がするものの、無視して続けます。$\lambda_4$は、中心が$C$であり、点$A$で$\Gamma$に接するレムニスケートです。この$\lambda_4$の焦点を$F_4,{F'}_{\! 4}$とおくと、定理1より$\lambda_3$の面積は$2\times F_1 F_4 \times F_1 {F'}_{\! 4}$と判ります。よって、ここからはレムニスケートの焦点たちがどのように位置するかだけを考えればよいです。
ここで、$C$の座標が$0$、$A$の座標が$1$となるような複素数平面(以下、$z$-平面と呼びます)を考えます。このとき、簡単な議論から$\Gamma$の中心$O_{\Gamma}$の座標は$\dfrac{3+\sqrt{3}i}{6}$と分かるので、$\dfrac{3+\sqrt{3}i}{6}=a^2$とおきましょう(ただし$0< \arg a <\pi$)。いま、レムニスケート$\lambda_4$の方程式を求めたいです。そのため、以下の補題を示しておきます。
$0$でない任意の整数$a$と複素数$c$を用意する。グラフ$G_a:|cz^a-1|=1$が点$U(1)$を通るとき、$G_a$の$U$における接線の傾きは$a$によらない。
$z=r(\cos\theta+i\sin\theta),$$c=r_c(\cos\theta_c+i\sin\theta_c)$と極形式表示すると、$G_a$のグラフを表す式は$\left|r_c r^a(\cos (a\theta+\theta_c)+i\sin (a\theta+\theta_c))-1\right|=1$と書ける。これが$U(1)$を通るので、$r=1,$$\theta=0$を代入して$\left|r_c(\cos\theta_c+i\sin\theta_c)-1\right|=1$$\Longrightarrow {r_c}^2-2r_c\cos \theta_c+1=1$$\Longrightarrow r_c=2\cos \theta_c$が必要である。
$G_a$の式の両辺を2乗し、整理していく。
$$\begin{align}
\left|r_c r^a(\cos (a\theta+\theta_c)+i\sin (a\theta+\theta_c))-1\right|^2&=1 \\
{r_c}^2 r^{2a}-2r_c r^a\cos (a\theta+\theta_c)+1&=1 \\
2\cos (a\theta+\theta_c)&=r_c r^a \\
\cos (a\theta+\theta_c)&=\cos \theta_c r^a \\
r&=\qty(\dfrac{\cos (a\theta+\theta_c)}{\cos \theta_c})^{\frac{1}{a}} \\
\end{align}$$
すなわち、$f(\theta)=\qty(\dfrac{\cos (a\theta+\theta_c)}{\cos \theta_c})^{\frac{1}{a}}$とおくと、$G_a$を表す極方程式は$r=f(\theta)$となる。
$$\begin{align}
\dfrac{d}{d \theta}f(\theta)
&=\dfrac{\frac{1}{a}(\cos (a\theta+\theta_c))^{\frac{1}{a}-1}}{(\cos \theta_c)^{\frac{1}{a}}}\left(-a\sin (a\theta+\theta_c)\right) \\
&=\dfrac{-(\cos (a\theta+\theta_c))^{\frac{1}{a}-1}\sin (a\theta+\theta_c)}{(\cos \theta_c)^{\frac{1}{a}}}
\end{align}$$であるから、$f'(0)=\dfrac{-(\cos \theta_c)^{\frac{1}{a}-1}\sin \theta_c}{(\cos \theta_c)^{\frac{1}{a}}}$$=-\tan \theta_c$となり、$G_a$のグラフにおける$\theta=0$付近の$r$の変化率は$a$によらない一定値$-\tan \theta_c$であると判明する。$\theta=0$のとき$r=1$であるから、これは示すべきことと同値である。$\blacksquare$
補題を示せたところで、以下の事実を確認しておきます(証明は各自で調べてください)。
・数式$\qty|\dfrac{z}{w}-1|=1$が$z$-平面上に描くグラフは、点$W(w)$を中心とし、原点を通る円である。
・数式$\qty|\dfrac{z^2}{w^2}-1|=1$が$z$-平面上に描くグラフは、2点$W(w),W'(-w)$を焦点とするレムニスケートである。
・焦点間の距離が$2d$であるレムニスケートの面積は$d^2$で与えられる。
この事実から、$\Gamma$を表す方程式は$\qty|\dfrac{z}{a^2}-1|=1$です。補題2の結果より、方程式$\qty|\dfrac{z^n}{a^2}-1|=1$で表されるグラフは、$n$の値によらず$\Gamma$と点$A(1)$で接しています。$n=2$のときにこの式はレムニスケートを表すので、$C(0)$を中心とし点$A$で$\Gamma$と接するレムニスケート、すなわち$\lambda_4$の方程式は$\qty|\dfrac{z^2}{a^2}-1|=1$と導かれます。ゆえに$F_4,{F'}_{\! 4}$の座標は$a,-a$のいずれかであり、一旦$F_4$の座標が$a$であると見なして問題ありません。
加えて、$F_1$の座標を$b$とおけば、$2\times F_1 F_4 \times F_1 {F'}_{\! 4}$$=2|b-a||b+a|$$=2\qty|b^2-a^2|$です。この$z$-平面上における$F_1$の座標を求められれば、定理1から直ちに$\lambda_3$の面積を求められるのです。
このまま突っ走ってもよいですが、敢えてさらなる工夫をしましょう。今度は辺$E_2 E_3$が$\Gamma$と点$F_1$で接するような正三角形$CE_2 E_3$を描いてみます。ただし、点の名前は反時計回りにつけました。

解ります。解りますよ。所謂「天下り」でしかなく、心の内で憤怒を滾らせる読者が現れるのも当然です。本当にすみません。落ち着いてください。
円周角や接弦定理を用いると$\triangle CAF_1 \sim \triangle CF_1 E_3$が判り、ここから$E_3$の座標は$b^2$です。したがって、線分$E_3 O_{\Gamma}$の長さは$\qty|b^2-a^2|$であるといえます。定理1で得た結果と併せると、$\lambda_3$の面積は$2E_3 O_{\Gamma}$である、ということになります。ここに至り、やっと$\lambda_2$を思い出します。すると、$\lambda_3$に関して紡いできた議論が同様に使えて、$\lambda_2$の面積は$2E_2 O_{\Gamma}$です。結局、求める面積比は$E_2 O_{\Gamma} : E_3 O_{\Gamma}$と書き換えられます。
さて、$AF_1=p,$$BF_1=q$とおきます。トレミーの定理から$CF_1=p+q$が判るので、$\triangle BF_1{F'}_{\! 1},$$\triangle BF_1 C$に余弦定理を用いると、
$$\begin{align}
&\left\{ \begin{aligned}
q^2+(2p+2q)^2-2q(2p+2q)\cos {60}^{\circ}&=2^2 \quad\dots({\rm i}) \\
q^2+(p+q)^2-2q(p+q)\cos {60}^{\circ}&=1^2 \quad\dots({\rm ii}) \\
\end{aligned}\right. \\
&\Longrightarrow\; 3q^2-4q(p+q)\cos {60}^{\circ}=0 \qquad(\because ({\rm ii})\times 4-({\rm i})) \\
&\Longrightarrow\; q(q-2p)=0 \;\Longrightarrow\; q=2p
\end{align}$$
を確かめられます。相似比より$\dfrac{E_2 F_1}{E_3 F_1}=\dfrac{BF_1}{AF_1}$ですから、$\dfrac{E_2 F_1}{E_3 F_1}=2$となります。ゆえに、以下の図において、$KN:LN$を求めればよいですね(点$N$は青い円の中心)。この値がそのまま答えになります。
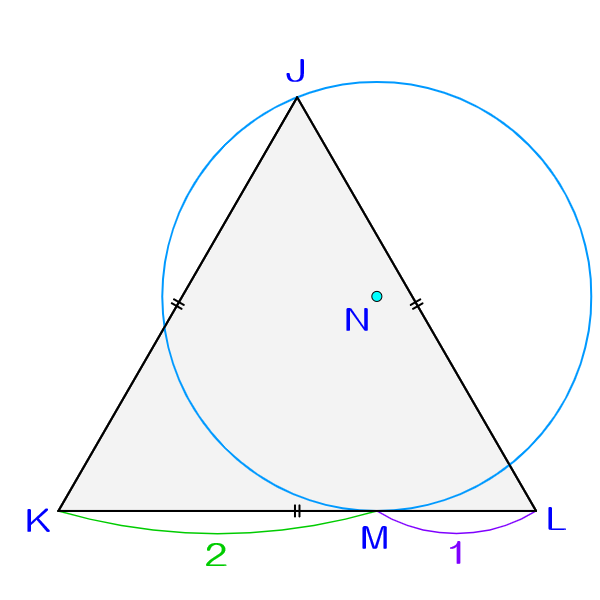
この図で、点$N$はある放物線に乗っています。それは、焦点が$J$、準線が$KL$の放物線です($\because$ 放物線は焦点からと準線からの距離が等しい点の軌跡)。よって、線分$KL$の中点を$O$とし、直線$KL$が$x$軸、直線$OJ$が$y$軸となるような$xy$-直交座標平面を考えると良さそうです(ただし点$N$が第1象限に含まれるように定めます)。
この座標平面において、件の放物線の式は対称性から$y=cx^2+d$と表せます。また、この放物線は明らかに2点$\qty(0,\dfrac{3\sqrt{3}}{4}),$$\qty(\dfrac{3}{2},\sqrt{3})$を通るので、
$$\begin{align}
\left\{ \begin{aligned}
\sqrt{3}&=\qty(\dfrac{3}{2})^2 c+d \\
\dfrac{3\sqrt{3}}{4}&=0^2 c+d
\end{aligned}\right.
\Longrightarrow\;
\left\{ \begin{aligned}
c &=\dfrac{\sqrt{3}}{9} \\
d &=\dfrac{3\sqrt{3}}{4}
\end{aligned}\right.
\end{align}$$
と求められるわけです。いま、計算するまでもなく$N$の$x$座標は$\dfrac{1}{2}$ですから、放物線の式に代入することで$y$座標が$\dfrac{7\sqrt{3}}{9}$と判ります。したがって、
$$\begin{align}
KN : LN
&= \sqrt{\qty(\dfrac{1}{2}+\dfrac{3}{2})^2+\qty(\dfrac{7\sqrt{3}}{9})^2} : \sqrt{\qty(\dfrac{1}{2}-\dfrac{3}{2})^2+\qty(\dfrac{7\sqrt{3}}{9})^2} \\
&= \sqrt{\dfrac{157}{27}} : \sqrt{\dfrac{76}{27}} = \sqrt{157}:2\sqrt{19} \\
\end{align}$$
を導出できて、これが問題Eの答えです。どうしてこれがラスボスでないのでしょうか。
おまけ・定理1の新証明
$z$の実部を$\Re(z)$、虚部を$\Im(z)$と表記します。以下の補題を考えてみましょう。
$\Re(l)=\Re(m)=\Re(n)$ならば、$\Re\qty(\overline{l}\qty(m^2-ln))$$=\qty(l-m)^{2}\Re(l)$である。
$\Re(l)=\Re(m)$より、ある実数$m_0$を用いて$m=l+m_0 i$とおける。
$$\begin{align}
\Re\qty(\overline{l}m^{2})
&=\Re\qty(\overline{l}\qty(l+m_{0}i)^{2})=\Re\qty(\overline{l}\qty(l^{2}-{m_{0}}^{2}+2lm_{0}i)) \\
&=\Re\qty(l^{2}\overline{l})-\Re\qty(\overline{l}{m_{0}}^{2})+2\Re\qty(l\overline{l}m_{0}i)=\qty|l|^{2}\Re(l)-\Re(l){m_{0}}^{2}
\end{align}$$
$$\begin{align}
\Re\qty(l\overline{l}n)=\qty|l|^{2}\Re(n)=\qty|l|^{2}\Re(l)
\end{align}$$
$$\begin{align}
\Longrightarrow\;\Re\qty(\overline{l}\qty(m^2-ln))
&=\Re\qty(\overline{l}m^{2})-\Re\qty(l\overline{l}n) \\
&=-\Re(l){m_{0}}^{2}=-\qty(\dfrac{m-l}{i})^{2}\Re(l)=\qty(l-m)^{2}\Re(l)
\quad\blacksquare
\end{align}$$
あまりにも唐突な内容でしたが、そういうものと思ってください。あとで補題3の有用性が判ります。
レムニスケート$L_1:\qty|\dfrac{z^2}{p^2}-1|=1$および$L_2:\qty|\dfrac{z^2}{q^2}-1|=1$を考え、$L_1$が点$K(1)$を通るように$p$を定めます。また、原点を通り$L_1$と点$K$で接する円を$\gamma$とすると、$\gamma$と$L_2$は原点でない2点で交わるものとします。中心が$K$であり先述の2交点を通るレムニスケート$L_3$を描き、$L_3$の面積を求めたいです。もしもこの場合に定理1の関係が成立していれば、すなわち$L_3$の面積が$2|p+q||p-q|$$=2\qty|p^2-q^2|$であれば、適切な相似拡大および回転移動により、すべての場合で定理1の成立を示せますね(各自で確かめましょう)。
まず、補題2より$\gamma$の方程式を$\qty|\dfrac{z}{p^2}-1|=1$と求められます。これは問題Eを解くときにも利用した考察ですね。それから、仮定より$L_1$は$K(1)$を通るので、$\qty|\dfrac{1}{p^2}-1|=1$$\Longleftrightarrow \Re\qty(p^2)=\dfrac{1}{2}$となります(行間がやや広いかも……)。いま、$\gamma$と$L_2$の交点のひとつを$S(s)$とすれば、$\gamma$の式に代入して$\qty|\dfrac{s}{p^2}-1|=1$$\Longleftrightarrow \Re\qty(\dfrac{p^2}{s})=\dfrac{1}{2}$、$L_2$の式に代入して$\qty|\dfrac{s^2}{q^2}-1|=1$$\Longleftrightarrow \Re\qty(\dfrac{q^2}{s^2})=\dfrac{1}{2}$も明らかです。
実部の等しい3つの数が得られたので、早速補題3を使いましょう。補題3で$(l,m,n)$$=\qty(p^2,\dfrac{p^2}{s},\dfrac{q^2}{s^2})$として、
$$\begin{align}
\Re\qty(\overline{p^2}\qty(\qty(\dfrac{p^2}{s})^2-p^2 \times \dfrac{q^2}{s^2})) &=\qty(p^2-\dfrac{p^2}{s})^{2}\Re(p^2) \\
\Re\qty(\dfrac{p^2-q^2}{s^2})\qty|p^4| &=\dfrac{1}{2}\qty(1-\dfrac{1}{s})^2 p^4 \quad\qty(\because\Re(p^2)=\dfrac{1}{2})
\end{align}$$
と計算します。……ここでIQを30ほど上げると、「もしかして、$L_3$の方程式って$\qty|\dfrac{(z-1)^2}{\frac{\overline{p^2}}{p^2}(p^2-q^2)}-1|=1$なのかな?」という恐ろしすぎるエスパーを発揮できるのです(注:本記事では無根拠の仮定や勘を「エスパー」と呼称します)。できるか。
このエスパーを確かめます。$\qty|\dfrac{(z-1)^2}{\frac{\overline{p^2}}{p^2}(p^2-q^2)}-1|=1$のグラフ(これを${L'}_{\! 3}$とします)はレムニスケートになり、その中心は$K$です。また、先程の結果を利用した
$$\begin{align}
\qty|\dfrac{(s-1)^2}{\dfrac{\overline{p^2}}{p^2}(p^2-q^2)}-1|
&=\qty|\dfrac{\qty(1-\dfrac{1}{s})^2 p^4}{\dfrac{p^2-q^2}{s^2}\qty|p^4|}-1| \\
&=\qty|\dfrac{2\Re\qty(\dfrac{p^2-q^2}{s^2})\qty|p^4|}{\dfrac{p^2-q^2}{s^2}\qty|p^4|}-1| \\
&=\qty|\dfrac{\Re\qty(\dfrac{p^2-q^2}{s^2})-\Im\qty(\dfrac{p^2-q^2}{s^2})i}{\Re\qty(\dfrac{p^2-q^2}{s^2})+\Im\qty(\dfrac{p^2-q^2}{s^2})i}|=1
\end{align}$$
という式変形から、$S$は${L'}_{\! 3}$に乗っています。さらに、原点でも$S$でもない$\gamma$と$L_2$の交点も、$S$と同様に${L'}_{\! 3}$に乗るといえます。すなわち${L'}_{\! 3}$は「中心が$K$であり$\gamma$と$L_2$の原点以外の2交点を通るレムニスケート」と判明し、$L_3$と${L'}_{\! 3}$が一致するのです。
そうなると、$L_3$の焦点間距離は$2\sqrt{\qty|\dfrac{\overline{p^2}}{p^2}(p^2-q^2)|}$$=2\sqrt{\qty|p^2-q^2|}$ですね($\because \qty|\dfrac{\overline{p^2}}{p^2}|=1$)。途中にアルティメットエスパーを挟みましたが、これで$L_3$の面積が$2\qty|p^2-q^2|$と示され、定理1の証明が完了しました。エスパー万歳。
次回予告
さあ、既に初級者どころか一部の幾何上級者までお断りしてしまいそうなT-GUESS Cup 4。難易度調整の失敗は誰の目にも明らかであり、一体誰に向けたコンテストなのか疑念が絶えませんね。
しかしながら、こんなものでは終わりません。まだ1問残っているのです。それこそが問題F(
こちら
から)。主催者の幾何力のすべてを詰め込んだ……だけでなく、少々ブーストをかけてただただただただただただ難しく仕上げた問題です。内心・外心・傍心がフルで登場しており、手をつける前から既に結構威圧されます。初手としてどう動くのが正解なのでしょうか。
上記の5問をすべて足したバイト数よりもさらに長い解説+α、どうかご期待くださいませ。
ご感想・ご指摘・巧妙な解法・マスタリング時の音圧の上げ方などがございましたら、是非ともコメントに残していってください。ここまでお読みいただき、ありがとうございました。
