文献あり

続・レムニスケート版『余弦定理』の提案＆過去の研究のまとめ

373

本記事を読む前に……

　可読性を上げるために、途中計算がかなりの割合で省かれています。まずは「へぇ、そうなるのか」程度の気持ちで読み進めてください。一通り議論の流れを浚ってから、順番に検算していくことを強く推奨します(推奨グレードＡ、レベルⅤ)。

　レムニスケート版『余弦定理』の提案　- Suggestion of "law of cosines" in lemniscate geometry - の投稿から早3ヶ月、当時の記事を読み返して気づいたことがあります。
　すなわち、
「なにこれ読みづらっ……」
ということです。
　重要な補題の証明を別記事に載せたり、不要な反転を定義して煩雑化させたり、誰にも伝わらないパロディを込めたり、まだまだエトセトラ。最早読ませる気がないといってよいでしょう。アレを解読できた人はむしろ何らかの団体から表彰されて然るべきです。

　と、いうことで。今回はレムニスケート版『余弦定理』01の証明を清書します。天下り的な発想を可能な限り避けて、ストレートに示していきます。
　残念ながら新発見は出てきません。ついでに過去のレムニスケート研究のまとめも載せますので、どうかご容赦ください。一応研究はしているのです……ただ元が4次曲線なので適当に座標計算しようとすると14万文字の方程式を解かなければいけなくなり見事に心を折られまして……。

定理の説明

清書されたレムニスケート版『余弦定理』

　$AB=x, AD=y$である平行四辺形$ABCD$の中心を$O$とし、2点$A,C$が焦点となるレムニスケートを$L_1$、2点$B,D$が焦点となるレムニスケートを$L_2$と定める。
　いま、$L_1$上に$O$でない点$P$をとると、$O$を通り$P$で$L_1$に接する円が、$L_2$と$O$でない2点$X,Y$で交わった。このとき、$P$を中心とし2点$X,Y$を通るレムニスケート$L_3$について、$L_3$の面積は$2xy$である。
▲白い点はレムニスケートの焦点です

　平行四辺形の内角も接点の位置も関係なく、$L_3$の面積が常に一定値$2xy$をとる、という定理です。改めて見ても非常に強い主張ですね。「余弦定理」らしさは消えましたが。
　さて、本定理を証明するべく、まずはいくつか補題を用意しましょう。

補題の準備

補題１（回転レムニスケートの一般形）

　$xy$座標平面にレムニスケート$L_1:\,\left(x^{2}+y^{2}\right)^{2}=x^{2}-y^{2}$を描く。$L_1$を原点中心に$\dfrac{1}{r}$倍して角度$\theta$だけ回転させたレムニスケート$L_2$の式は、

$L_2:\,r^{2}\left(x^{2}+y^{2}\right)^{2}=\left(x^{2}-y^{2}\right)\cos2\theta+2xy\sin2\theta$

で与えられる。
※$L_1$は長軸が$x$軸に平行で、かつその長さが$1$となる原点中心のレムニスケートになります。

補題１の証明

　一般に、方程式$f(x,y)=0$が$xy$平面上に描く図形$S_1$を考えると、$S_1$を原点中心に$\dfrac{1}{a}$倍した図形$S_2$の方程式は$\displaystyle f\left(ax,ay\right)=0$で与えられる。また、$S_1$を原点中心に角度$z$だけ回転させた図形$S_3$の方程式は$f\left(x\cos z -y\sin z,x\sin z+y\cos z\right)=0$で与えられる02 03。
　$g(x,y)=\left(x^{2}+y^{2}\right)^{2}-\left(x^{2}-y^{2}\right)$とおくと、$g(x,y)=0$によって描かれる曲線は$L_1$である。したがって、$L_2$の方程式は

$$ f\left(rx\cos\theta -ry\sin\theta,rx\sin\theta+ry\cos\theta\right)=0$$

と表せて、これを変形すれば証明が完了する(計算略)。$\blacksquare$

　補題１から、以下の式で定義される曲線$\lambda_1,\lambda_2,\lambda_3$はいずれも原点中心のレムニスケートになりますね($t,u$は正の実数)。

$$ \begin{align} \lambda_1:\, \;\;\left(x^{2}+y^{2}\right)^{2}&=x^{2}-y^{2} \\ \lambda_2:\, u\left(x^{2}+y^{2}\right)^{2}&=\left(x^{2}-y^{2}\right)\cos 2t+2xy\sin 2t \\ \lambda_3:\, u\left(x^{2}+y^{2}\right)^{2}&=\left(x^{2}-y^{2}\right)\left(u-\cos 2t\right)+2xy\sin 2t \end{align}$$

　$\lambda_1$は補題１の$L_1$と同じ式です。いま言及した$\lambda_1,\lambda_2,\lambda_3$はこれ以降の補題で何度か登場するので、覚えておきましょう。

補題２（レムニスケートに接する円の媒介変数表示）

　$\lambda_1$上に原点でない点$P$をとると、$P$の座標はパラメータ$p$を用いて

$\displaystyle P=\left(\frac{\sec p}{\sec^{2} p+\tan^{2} p},\frac{\tan p}{\sec^{2} p+\tan^{2} p}\right)$

と表せる。さらに、$p$を固定し、パラメータ$k$を用いて$$ \alpha=k\tan p+\sec p,\, \beta=k\sec p+\tan p$$なる実数$\alpha,\beta$を定めると、$$ (x,y)=\left(\frac{\alpha}{\alpha^{2}+\beta^{2}},\frac{\beta}{\alpha^{2}+\beta^{2}}\right),\,\left(\frac{k\beta}{\alpha^{2}+\beta^{2}},\frac{k\alpha}{\alpha^{2}+\beta^{2}}\right)$$はいずれも「原点を通り$P$で$\lambda_1$と接する円(から1点を除いたもの)」の媒介変数表示となる。

補題２の証明

　$P$の$x$座標と$y$座標を$\lambda_1$の式の両辺に代入すると等号が成立するため(計算略)、補題の前半が示される。
　「原点を通り$P$で$\lambda_1$と接する円」を$\Gamma$とする。ここで

$\Gamma':\, x^{2}+y^{2}=x\sec p-y\tan p$

なる円$\Gamma'$を考えると、$\Gamma'$の式の両辺を2乗して$\lambda_1$の式と比較することで

$x^{2}-y^{2}=\left(x\sec p-y\tan p\right)^2$

すなわち$\left(y-x\sin p\right)^2=0$が従い、$\Gamma'$と$\lambda_1$の共有点は直線$y=x\sin p$上にのみ存在するといえる。原点$O$および$P$は$\Gamma'$に乗っているため(計算略)、$\Gamma'$と$\lambda_1$の共有点はこの2点に限られる。
　いま$O$において、$\Gamma'$の接線の傾きは$\csc p$であり(計算略)、$\lambda_1$の接線の傾きは$\pm 1$であるから、$O$の近傍で$\Gamma'$は$\lambda_1$の外部を通ることが分かる($\because \left|\csc p\right|>1$)。よって、$\Gamma'$は決して$\lambda_1$の内部を通らず、$P$は$\Gamma'$と$\lambda_1$の接点でなければならない。ゆえに、$\Gamma$と$\Gamma'$は一致する。
　　補題の後半を示そう。任意の$k$に対して、$\displaystyle Q_1=\left(\frac{\alpha}{\alpha^{2}+\beta^{2}},\frac{\beta}{\alpha^{2}+\beta^{2}}\right)$および$\displaystyle Q_2=\left(\frac{k\beta}{\alpha^{2}+\beta^{2}},\frac{k\alpha}{\alpha^{2}+\beta^{2}}\right)$が$\Gamma'(=\Gamma)$に乗ることを確かめられる(計算略)。直線$OQ_1,OQ_2$の傾きがとりうる値の範囲を考えることで、$Q_1$は$O$を除いた$\Gamma$の全体を、$Q_2$は$P$を除いた$\Gamma$の全体を、それぞれ動くといえる(計算略)。これが示すべきことであった。$\blacksquare$

▲$Q_1,Q_2$が点線で記した円($\Gamma$)に乗っています

補題３（２つのレムニスケートが作り出す関係）

　補題２で定義した$P, \alpha, \beta$はそのまま用いる。2点$Q_1,Q_2$を

$Q_1=\left(\dfrac{\alpha}{\alpha^{2}+\beta^{2}},\dfrac{\beta}{\alpha^{2}+\beta^{2}}\right),\,Q_2=\left(\dfrac{k\beta}{\alpha^{2}+\beta^{2}},\dfrac{k\alpha}{\alpha^{2}+\beta^{2}}\right)$

で定める。
　このとき、$Q_1$が$\lambda_2$上にあるならば、$Q_2$は$\lambda_3$上にある。

補題３の証明

　$\lambda_2$の式の右辺を$f_{\lambda_2}\left( x,y\right)$、$\lambda_3$の式の右辺を$f_{\lambda_3}\left( x,y\right)$とおく。$$ f_{\lambda_3}\left( x,y\right)=\left(x^{2}-y^{2}\right)u+f_{\lambda_2}\left( y,x\right)$$と変形できるので、$\alpha_1=\dfrac{k\alpha}{\alpha^{2}+\beta^{2}},$ $\beta_1=\dfrac{k\beta}{\alpha^{2}+\beta^{2}}$とおけば、$$ f_{\lambda_3}\left( \beta_1 ,\alpha_1 \right)=\left({\beta_1}^{2}-{\alpha_1}^{2}\right)u+k^2 f_{\lambda_2}\left( \dfrac{\alpha}{\alpha^{2}+\beta^{2}},\dfrac{\beta}{\alpha^{2}+\beta^{2}}\right)$$が成立する。$Q_1$が$\lambda_2$上にあるとき、$\lambda_2$の式の両辺を比較すると$$ f_{\lambda_2}\left( \dfrac{\alpha}{\alpha^{2}+\beta^{2}},\dfrac{\beta}{\alpha^{2}+\beta^{2}}\right)=u\left(\left(\dfrac{\alpha}{\alpha^{2}+\beta^{2}}\right)^2+\left(\dfrac{\beta}{\alpha^{2}+\beta^{2}}\right)^2\right)^2=\dfrac{u}{k^4}\left({\alpha_1}^2+{\beta_1}^2\right)^2$$が分かり、これと先程の式を併せれば$$\begin{align} f_{\lambda_3}\left( \beta_1 ,\alpha_1 \right) &=\left({\beta_1}^{2}-{\alpha_1}^{2}\right)u+\dfrac{u}{k^2}\left({\alpha_1}^2+{\beta_1}^2\right)^2 \\ &=\dfrac{k^{2}u\left(\beta^2-\alpha^2\right)}{\left(\alpha^2+\beta^2\right)^2}+\dfrac{u}{k^2}\left({\alpha_1}^2+{\beta_1}^2\right)^2 \\ &=\dfrac{\left( k^4-k^2\right) u}{\left(\alpha^2+\beta^2\right)^2}+\dfrac{u}{k^2}\left({\alpha_1}^2+{\beta_1}^2\right)^2 \\ &=\dfrac{\left( k^2-1\right) u}{k^2}\left({\alpha_1}^2+{\beta_1}^2\right)^2+\dfrac{u}{k^2}\left({\alpha_1}^2+{\beta_1}^2\right)^2 \\ &=u\left({\alpha_1}^2+{\beta_1}^2\right)^2 \end{align}$$が従うため、$u\left({\beta_1}^2+{\alpha_1}^2\right)^2=f_{\lambda_3}\left( \beta_1 ,\alpha_1 \right)$を確認できて補題が示される。ただし、途中の変形に$\beta^2-\alpha^2=k^2-1$および${\alpha_1}^2+{\beta_1}^2=\dfrac{k^2}{\alpha^{2}+\beta^{2}}$を用いた(計算略)。$\blacksquare$

補題４（２つの点がある定直線について対称であること）

　補題２・補題３で定義した$P, Q_1, Q_2$はそのまま用いる。直線$l$を

$l:\, 2\left(x+y\sin p\right)=\cos p$

で定めると、$Q_1$と$Q_2$は直線$l$について対称な位置にある。
※　直線$l$は線分$OP$の垂直二等分線になっています(計算略)。

補題４の証明

　直線$Q_1 Q_2$の傾きは$\sin p$であるから(計算略)、$Q_1 Q_2 \perp l$といえる。
　線分$Q_1 Q_2$の中点を$Q_M$とすると、

$$ \begin{align} Q_M = \left(\frac{\alpha+k\beta}{2\left(\alpha^{2}+\beta^{2}\right)},\frac{k\alpha+\beta}{2\left(\alpha^{2}+\beta^{2}\right)}\right) \end{align}$$

と表せる。いま、これを$l$の式の左辺に代入してみれば、$$ \begin{align} &2\left(\frac{\alpha+k\beta}{2\left(\alpha^{2}+\beta^{2}\right)}+\frac{k\alpha+\beta}{2\left(\alpha^{2}+\beta^{2}\right)}\sin p\right) \\ &\quad\qquad =\frac{\left(k\sin p+1\right)\alpha+\left(k+\sin p\right)\beta}{\alpha^{2}+\beta^{2}} \\ &\quad\qquad =\frac{\left(k\tan p+\sec p\right)\alpha+\left(k p+\tan p\right)\beta}{\alpha^{2}+\beta^{2}}\cos p \\ &\quad\qquad =\frac{\alpha^{2}+\beta^{2}}{\alpha^{2}+\beta^{2}}\cos p=\cos p \end{align}$$のように等号の成立を確かめられる。したがって、$Q_M$は$l$上にあり、$Q_1 Q_2 \perp l$と併せて補題を証明できる。$\blacksquare$

▲$O,P$および$Q_1,Q_2$は$l$に関してそれぞれ対称です

少々の休憩

　はい、ここまで補題補題補題補題と続いたため、多くの読者は疲労困憊に陥っているはずです。一休みして雑談でもしましょう。

　さて、私がレムニスケートに注目した経緯を。2018年頃まで、私は幾何が大の苦手でした。折角補助線を引けても使い道が分からず、「図形問題は観賞用」という歪んだ認知のもとで育ってきました。
　しかしながら、丁度その頃、『図形問題を解けるようにならなければいけない状況』が発生しました。他の大問を選択すると計算ミスで壊滅するからです。いきなり何の話だ、と思われた方は聞き流してください。
　かくして、日夜図形と格闘し、不足していた演習量を取り戻すことに。元々「観賞用」と語るだけあって、幾何自体は非常に好みでした。件の『状況』が解消した後も幾何に嵌り続けて、気がつけば2020年の秋を迎えていたものです。その間、算数オリンピックの過去問から幾何を抽出して一般化を試みたり、無謀にもIMO(国際数学オリンピック)の3番級幾何に特攻して砕け散ったり、聞き齧っただけの『外心３つ法』を実践してみたり、と色々精進してまいりました。

　わざわざ2020年の秋を強調した辺りで、賢明な皆様は「ああ、何か転機が有ったのかな」と察したことでしょう。概ね正解で、2020年の秋は私が2次曲線を研究しはじめた時期になります。三角形の傍心がある楕円の準線に乗ることを知って、初等幾何と2次曲線の融合を図りました。先行研究04も読み耽り、この頃から2問/月のペースで2次曲線に基づいた幾何作問を続けている次第です。

　そして、2022年の初夏。Wikipediaで様々な記事を読んでいるうちに、ふと気になる一節がありました05。

The lemniscate is the circle inversion of a hyperbola and vice versa.

　和訳すると「レムニスケートは双曲線を円で反転した曲線であり、逆もまた然り」です。厳密にいえば直角な双曲線の反転でしかレムニスケートは得られないのですが、それはそれとして、私はこう考えました。
「今までの研究、使えるのでは……？」
　そう。双曲線は2次曲線なのです。2年近く続けてきた研究の中で、私は双曲線に関する知見を多く得ていました。それらをそのまま反転すれば、レムニスケートの世界に踏み込めるのです。さながら異世界に転生して無双する主人公のような気持ちで、知る限りの構図をひたすら反転していきました。その多くはただ煩雑になるだけでしたが、時折「なんだこれは」と呟きたくなる性質もあり、この方針の正しさを裏づけてくれました。

　今回のテーマであるレムニスケート版『余弦定理』は、そういった試行錯誤のもとに生まれたものです。双曲線に関する構図(過去の記事で楕円バージョンを扱っています)のひとつが、偶然にもレムニスケートに効き、原石と呼ぶべき性質を発見できました。その「原石」を1年余りかけて切って磋いて琢いて磨いて、定理を仕上げました。したがって、本定理に対する私の愛着は凄まじいです。もしも既出の性質であったならば、先駆者へ最大限の賛辞と尊敬を送るとともにひっそりと枕を濡らすことでしょう。

　以上、別に数学専攻でもない一般人のお気持ちエッセイでした。閑話休題して、そろそろ定理の証明に戻りますね。

証明の構成

必要な定義を補題から流用

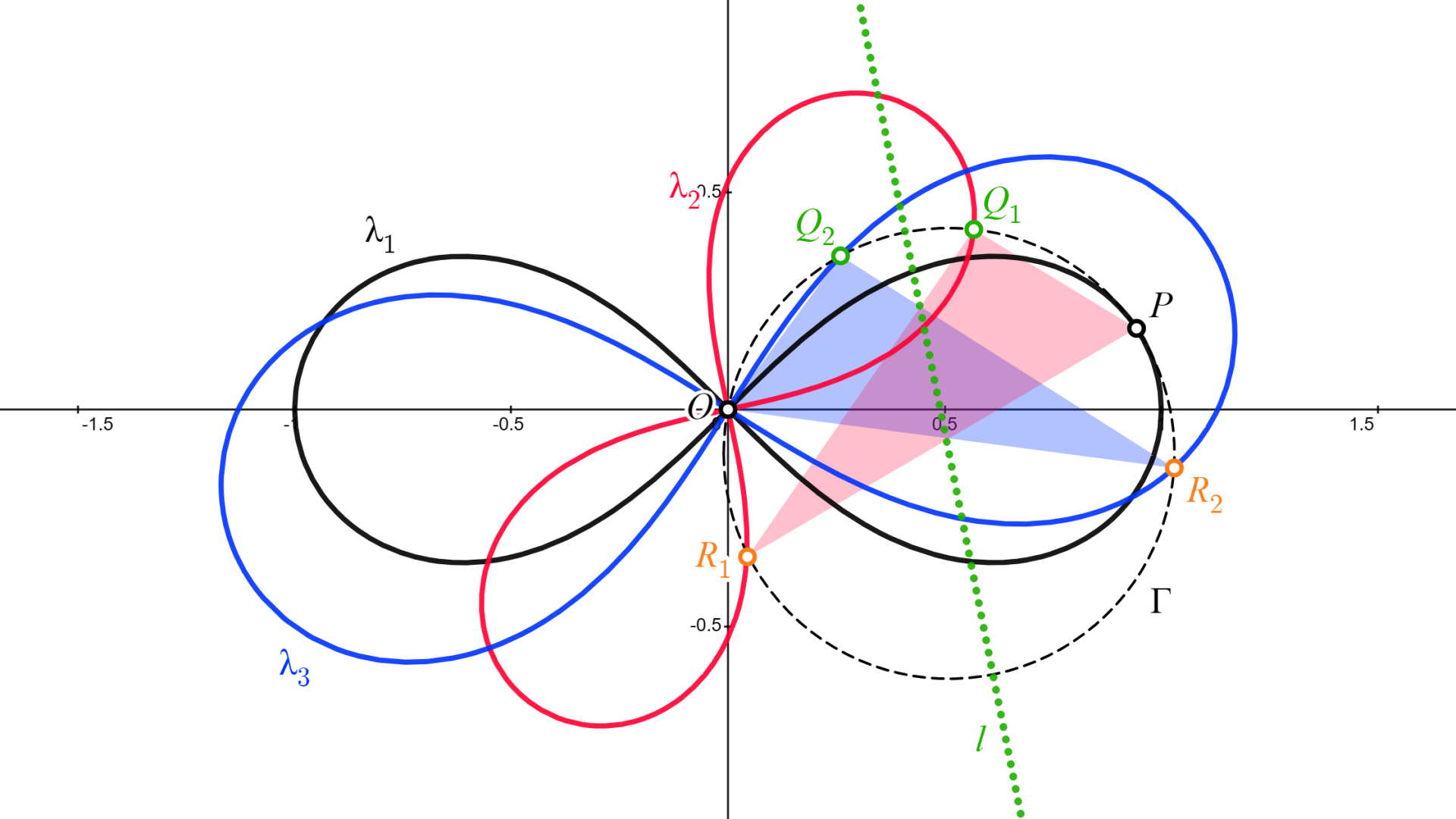▲この図が描ければ示せたも同然です

「補題の準備」のセクションで用意した$\lambda_1,\lambda_2,\lambda_3$を$xy$座標平面上に描きましょう(上図参照)。補題１より、$\lambda_2$は「原点$O$に関して$\lambda_1$を$\dfrac{1}{\sqrt{u}}$倍し角度$t$だけ回転させたレムニスケート」となります。$t,u$は任意の正の値をとるので、$\lambda_2$の向きと大きさも任意に変えられるわけです。したがって、$\lambda_1,\lambda_2$の焦点計4つで作られる平行四辺形も任意の形になりうるため、$t,u$を任意に固定してもとの定理の成立を確かめれば必要十分ですね。

　その他、補題２で定義した$P,\alpha,\beta,\Gamma$、補題３で定義した$Q_1,Q_2$、および補題４で定義した$l$も、まとめて流用します(上図参照)。ただし、補題３を使いたいので、$Q_1$が$\lambda_2$に乗るようにパラメータ$k$を定めることとします($\Gamma$と$\lambda_2$が$O$でない2点で交わった場合のみを考えているため、そのような$k$が必ず存在します)。

補題を限界まで使い倒す

　いま、補題２から$Q_1,Q_2$はいずれも$\Gamma$上にあります。$Q_1$は$\lambda_2$にも乗っているため、補題３から$Q_2$は$\lambda_3$に乗っています。言い換えれば、$\Gamma$と$\lambda_2$の交点の1つが$Q_1$であり、$\Gamma$と$\lambda_3$の交点の1つが$Q_2$です。
　ここで補題４を用いると、$O$と$P$、$Q_1$と$Q_2$はいずれも$l$に関して対称な点の組となるので、$PQ_1=OQ_2$が分かります。

　$\Gamma$と$\lambda_2$の交点で、$O$でも$Q_1$でもないものが1つありますね。これを$R_1$と定義すれば、補題２より、パラメータ$k'$を適当に定めて$$ \alpha'=k'\tan p+\sec p,\, \beta'=k'\sec p+\tan p$$とすることで、$R_1$の座標を$$ R_1=\left(\dfrac{\alpha'}{\alpha'^{2}+\beta'^{2}},\dfrac{\beta'}{\alpha'^{2}+\beta'^{2}}\right)$$と表せます。実はこの$R_1$に対しても補題３の主張が使えまして($k$が$k'$になっただけ)、$$ R_2=\left(\dfrac{k'\beta'}{\alpha'^{2}+\beta'^{2}},\dfrac{k'\alpha'}{\alpha'^{2}+\beta'^{2}}\right)$$なる点$R_2$は、$\Gamma$と$\lambda_3$の交点(のうち$O$でも$Q_2$でもないもの)になるのです。ゆえに、補題４と同様に考えれば、$R_1$と$R_2$もまた$l$に関して対称な点の組と判明します。つまり、$PR_1=OR_2$かつ$Q_1 R_1=Q_2 R_2$です。

　したがって、3辺が等しいので$\triangle PQ_1 R_1 \equiv \triangle OQ_2 R_2$を示せます。この2つの三角形は、$l$に関する対称移動で互いに移りあうのです。

誰にでもできる計算の時間

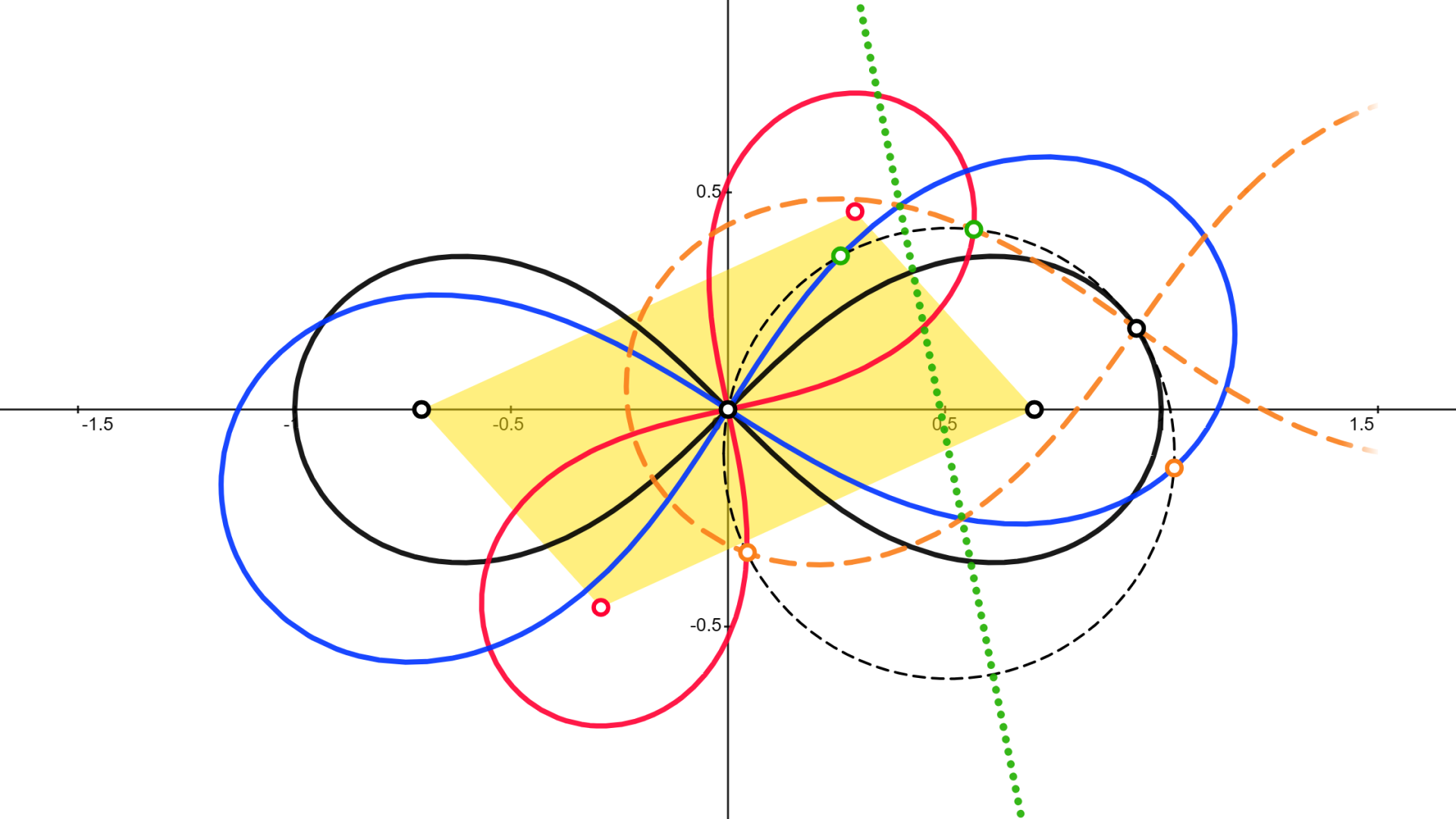▲1つ上の図に後述する$A,B,C,D,{\lambda_3}'$を加えました

　$\lambda_1$の焦点を$A,C$と、$\lambda_2$の焦点を$B,D$と、それぞれ定めます。もとの定理と対応させると、「$P$を中心とし2点$Q_1, R_1$を通るレムニスケート」の面積が$2\times AB \times AD$であればよいですね。そのようなレムニスケートを${\lambda_3}'$とおきましょう。
　ところで、直前のセクションを思い出してください。$\triangle PQ_1 R_1$を$l$に関して対称移動させれば、$\triangle OQ_2 R_2$へ移るのでした。すなわち、「$O$を中心とし2点$Q_2,R_2$を通るレムニスケート」を$l$に関して対称移動させれば「$P$を中心とし2点$Q_1, R_1$を通るレムニスケート」になります。……面倒なので簡潔に言い直すと、$\lambda_3$と${\lambda_3}'$が$l$に関して対称です。すなわち、$\lambda_3$の面積が$2\times AB \times AD$であることを示せば証明完了です。漸く終わりが見えてきました。

　レムニスケートの焦点や面積に関する情報を得るため、Wikipediaを参照します05。

The equations can be stated in terms of the focal distance $c$ or the half-width $a$ of a lemniscate. These parameters are related as $a=c\sqrt{2}$.

Its Cartesian equation is (up to translation and rotation):$$ \begin{align} \left(x^2+y^2\right)^2&=a^2\left(x^2-y^2\right) \\&=2c^2\left(x^2-y^2\right)\end{align}$$

The area enclosed by the lemniscate is $a^2=2c^2$.

　長いので和訳を割愛しますが、要は$\lambda_1$の焦点が$\left(\pm\dfrac{1}{\sqrt{2}},0\right)$であることと、その面積が$1$であることが述べられています。加えて、先述の通り$\lambda_2$は「原点$O$に関して$\lambda_1$を$\dfrac{1}{\sqrt{u}}$倍し角度$t$だけ回転させたレムニスケート」であるため、$\lambda_2$の焦点は$\left(\pm\dfrac{\cos t}{\sqrt{2u}},\pm\dfrac{\sin t}{\sqrt{2u}}\right)$にあることが言えますね(計算略、複号同順)。以上より、$$ A=\left(\dfrac{1}{\sqrt{2}},0\right),\, B=\left(\dfrac{\cos t}{\sqrt{2u}},\dfrac{\sin t}{\sqrt{2u}}\right),\, D=\left(-\dfrac{\cos t}{\sqrt{2u}},-\dfrac{\sin t}{\sqrt{2u}}\right) $$としてよく、このとき$$ 2\times AB \times AD=\dfrac{\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2} 2t}}{u}$$です(計算略)。結構シンプルになりました。

　さて、$\lambda_3$の式を再掲します。$$ \begin{align} \lambda_3:\, u\left(x^{2}+y^{2}\right)^{2}=\left(x^{2}-y^{2}\right)\left(u-\cos 2t\right)+2xy\sin 2t \end{align}$$　それぞれの係数に著しい見覚えがありますね。高校で「三角関数の合成」の単元を習った方ならば既に直感を得たと思われますが、この式の両辺を$\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2} 2t}$で割ると$$ \begin{align} \mathrm{(LHS)}&=\frac{u}{\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2}2t}}\left(x^{2}+y^{2}\right)^{2} \\ \mathrm{(RHS)}&=\left(x^{2}-y^{2}\right)\frac{u-\cos 2t}{\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2}2t}}+2xy\frac{\sin 2t}{\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2}2t}} \\ &=\left(x^{2}-y^{2}\right)\cos 2v+2xy\sin 2v \qquad\left(\tan 2v=\frac{\sin 2t}{u-\cos 2t}\right) \end{align}$$と変形できます。したがって、補題１を用いて、$\lambda_3$の面積は$\lambda_1$の面積の$\dfrac{\sqrt{\left(u-\cos 2t\right)^{2}+\sin^{2} 2t}}{u}$倍であると導けるのです。1番最初に示した性質が1番最後に出てくると謎のロマンを覚えますね。

　$\lambda_1$の面積は$1$ですから、ここに至ってやっと証明の全工程が終わりました。$\blacksquare$

回顧の濁流

　お疲れ様でした。長い証明が済んで、疲労困憊という語が過去のものとなるくらいにお疲れのことと拝察します。
　ですが、本記事のタイトルには『過去の研究のまとめ』という文字列がありましたね。要するにまだ続くのです。なんという無遠慮。
　せめてもの慈悲として、ここからは頭を使わなくてもよいように、証明を省き過去に発見した事実のみを羅列していきます(既出であったものは記しません)。

【共焦点の楕円とレムニスケートで成立する関係】06

　焦点を共有するレムニスケート$L$と楕円$E$が接している。これらの焦点を$F,F'$とし、$E$の中心および$F'$を通る円$C$を描く。$F'$を通る$C$の接線が$E$と交わる点を$P,Q$とし、$E$の中心でない$L$と$C$の交点を$R,S$とする。
　このとき、$\angle PFQ + {180}^{\circ} = 2\angle RF'S$が成立する。

【レムニスケートと4点で交わる直線が作る関係】07

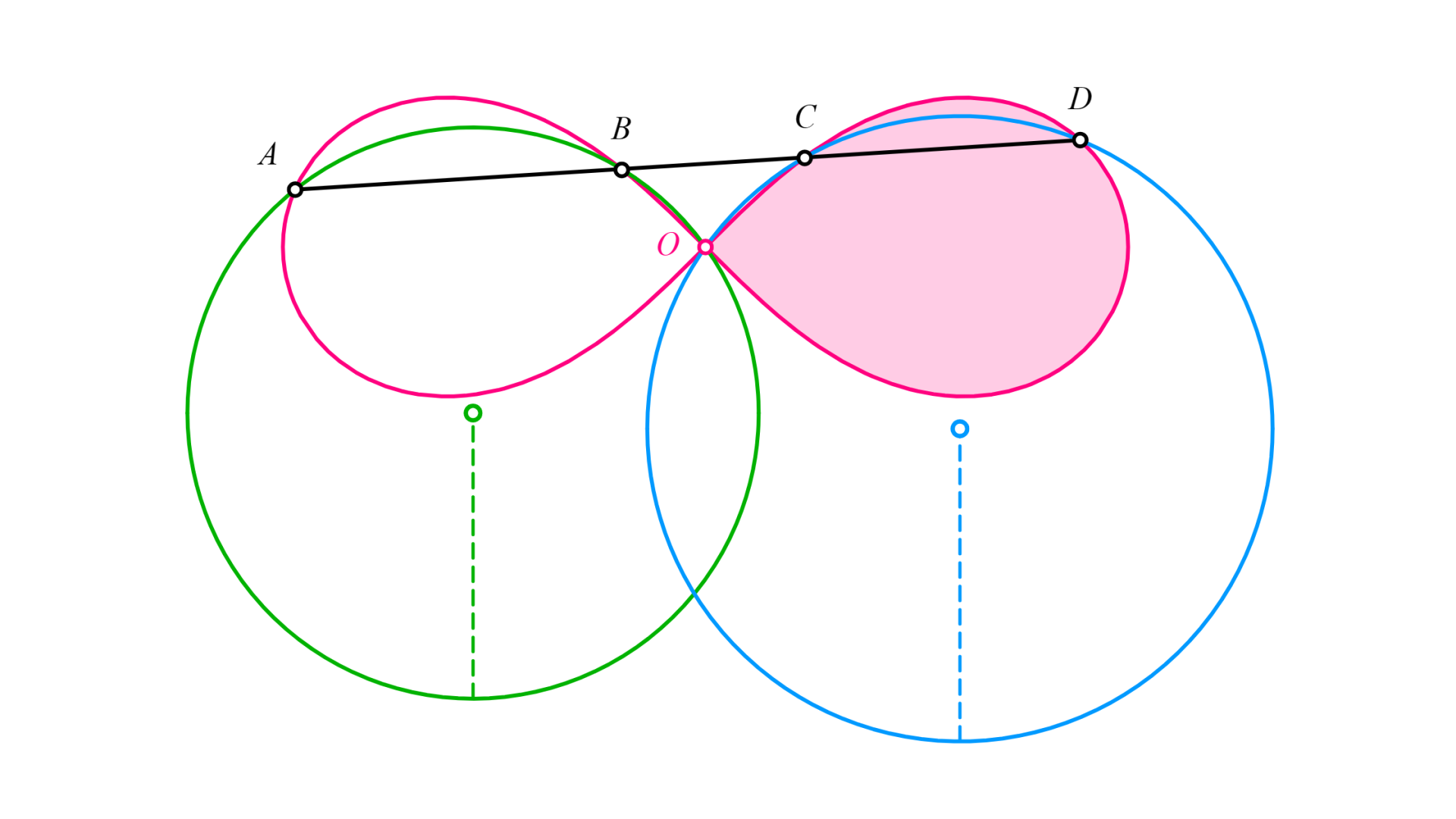
　レムニスケート$L$の中心を$O$とする。ある直線と$L$が4点$A,B,C,D$で交わっており、$\triangle OAB,\triangle OCD$の外接円の半径はそれぞれ$x,y$であった。
　このとき、$L$の面積は$2xy$である。

【3つのレムニスケートにおいて成り立つ関係】01 08

　$AB=x, AD=y$である平行四辺形$ABCD$の中心を$O$とし、2点$A,C$が焦点となるレムニスケートを$L_1$、2点$B,D$が焦点となるレムニスケートを$L_2$と定める。
　いま、$L_1$上に$O$でない点$P$をとると、$O$を通り$P$で$L_1$に接する円が、$L_2$と$O$でない2点$X,Y$で交わった。
　このとき、$P$を中心とし2点$X,Y$を通るレムニスケート$L_3$について、$L_3$の面積は$2xy$である。

　最後に述べたのが、今回証明したレムニスケート版『余弦定理』ですね。
　こうして列挙してみると、我ながら、かなりハイペースで研究が進んでいるように感じます。半ダース/日のペースで定理を見つけたインド出身の某数学者には劣るものの、特に3つ目などは非自明さの極致に近いと自負しています。
　楕円積分さえまともに修めていない身で、どうしてこうも多くの性質と巡り会えたのか。それは偏に、レムニスケートという領域が莫大な宝を秘めた鉱脈であったためでしょう。まあ、つまりは……全国の研究者さん、成果を先取りするならば今ですよ。