レムニスケート版『余弦定理』の提案 - Suggestion of "law of cosines" in lemniscate geometry -
本記事の参考文献は私自身が過去に執筆した記事1編のみです。可能な限り読みやすくなるよう配慮しましたが、説明不足で理解の難しい箇所があればそちらの記事も参考になさってください。それと追記は必見です。
お久しぶりです、
匿(Tock)
と申します。タイトルの通り、レムニスケート研究の中で記録すべき事項ができたので、こうして筆を執っている次第です。
本記事の内容について開示すべき利益相反(COI)はありません。また、普段は「だ・である体」で書いている身ですが、今回は試しに「です・ます体」で書いてみます。皆様の反応を見て次回以降の文体を決めようかと。
要約
3つの レムニスケート を適切に配置したとき、余弦定理に類似した関係が成立することを発見しました。この関係をレムニスケート版『余弦定理』と呼ぶことを提案し、また本定理の証明および系のいくつかを紹介します。
経緯
以前投稿した『 3つのレムニスケートが生み出す『a^2+b^2=c^2』について - New Pythagorean-like theorem in lemniscate geometry - 』で、三平方の定理(Pythagorean theorem)とよく似た定理を発表し、証明しました。折角なので以下に掲載しておきます。
点$O$を中心とするレムニスケート$L_1,L_2$が直交している。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点を$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1,L_2,L_3$の周長をそれぞれ$a,b,c$とすると、$a^2+b^2=c^2$ が成立する。
▲発表から9ヶ月、未だ誰にも利用されていません
さて、記事投稿後、上の記事の共同研究者である立見鶏氏から、Twitterにて
「次はレムニスケート余弦定理でしょうかね…」(原文そのまま)
というダイレクトメッセージが届きました。
確かに、普通の三平方の定理は普通の余弦定理の特別なケースである、という捉え方ができるため、『三平方の定理』を見つけたならばその調子で『余弦定理』も見つけられる、と考えるのが自然です。ゆえに私のほうも
「よし、(皆目見当もつかないけれど一応)探してみますか!」
と奮起いたしました。なんと単純な動機でしょうか。昔話でももう少し捻りを加えますね。
そこから8ヶ月余りが経って、気づけば季節は晩春。最早何千個のレムニスケートを描いたか分からなくなった頃、唐突に『余弦定理』の天啓が降ってきました。
それは予想以上に単純で、しかし長らく思い至れなかった形。恐らく読者の皆様も、ひとたび図を見てしまえば「どうしてこれを思いつけないのか」と言いたくなることでしょう。つい私も「この8ヶ月を返せ」と思ってしまいました。
ということで、いよいよ定理の紹介です。念のため記しますが、私の調べた限りで先行研究は見つかっていません。
定理
点$O$を中心とするレムニスケート$L_1,L_2$が角度$\theta$をなして交わっている。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点が2つできるとき、それを$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1,L_2,L_3$の周長をそれぞれ$a,b,c$とすると、$a^4+b^4-2 a^2 b^2 \cos 2\theta =c^4$ が成立する。
▲$L_2$が少し回転しましたね
『三平方の定理』との相違点を赤色で表示しています。
……我々のよく知る余弦定理の式 $a^2+b^2-2ab \cos \theta =c^2$ と比較すると、何となく差異がありますね。次数が2倍されて、偏角も2倍です。まあ、数式のビジュアルが余弦定理に近いので、レムニスケート版『余弦定理』と呼んでも差し支えないでしょう。ただ、ここまでアバウトな判断を許すなら${\rm sl}^2 \theta + {\rm cl}^2 \theta + {\rm sl}^2 \theta \, {\rm cl}^2 \theta = 1$をPythagorean-likeと認めてあげてもよかったのでは、とは思わなくもないです。
この定理から先述のレムニスケート版『三平方の定理』が得られることは明らかです。$\theta ={90}^{\circ}$のときを考えると、
$$ \begin{align*}c^4 &=a^4+b^4-2 a^2 b^2 \cos (2 \times {90}^{\circ}) \\[6pt] &=a^4+b^4+2 a^2 b^2 \\[6pt] &=\left( a^2+b^2 \right)^2 \\ \end{align*}$$
から$a^2+b^2=c^2$が導出されます($\because a, b, c>0$)。
証明
以下$xy$直交座標平面上で考え、円$\Gamma$に関する反転でオブジェクト$\sigma$が移る場所を${\rm inv}(\sigma , \Gamma)$と表します。
双曲線の接線上にある2点の関係
$p$を任意の実数とし、直角な双曲線$\eta_1:\,$$x^2-y^2=1$上に点$\displaystyle P=\left(\frac{1}{\cos\left(p\right)},\tan\left(p\right)\right)$ をとります。$P$を通る$\eta_1$の接線$l:\,$$\displaystyle \frac{1}{\cos\left(p\right)}x-\tan\left(p\right)y=1$を描き、$l$上に$P$と異なる任意の点$\left(x_{1},y_{1}\right)$をとることにすれば、ある実数$k \neq 0$を用いて
$$ \left(x_{1},y_{1}\right)=\left(\tan\left(p\right)k+\frac{1}{\cos\left(p\right)},\,\frac{k}{\cos\left(p\right)}+\tan\left(p\right)\right)$$
と表せます。また、今後の議論のために
$$ \left(x_{2},y_{2}\right)=\left(\frac{\tan\left(p\right)}{k}+\frac{1}{\cos\left(p\right)},\,\frac{1}{k\cos\left(p\right)}+\tan\left(p\right)\right)$$
なる実数$x_{2},y_{2}$を定義し、点$\displaystyle M=\left(x_{1},y_{1}\right), $ $\displaystyle N=\left(x_{2},y_{2}\right)$と名付けましょう。
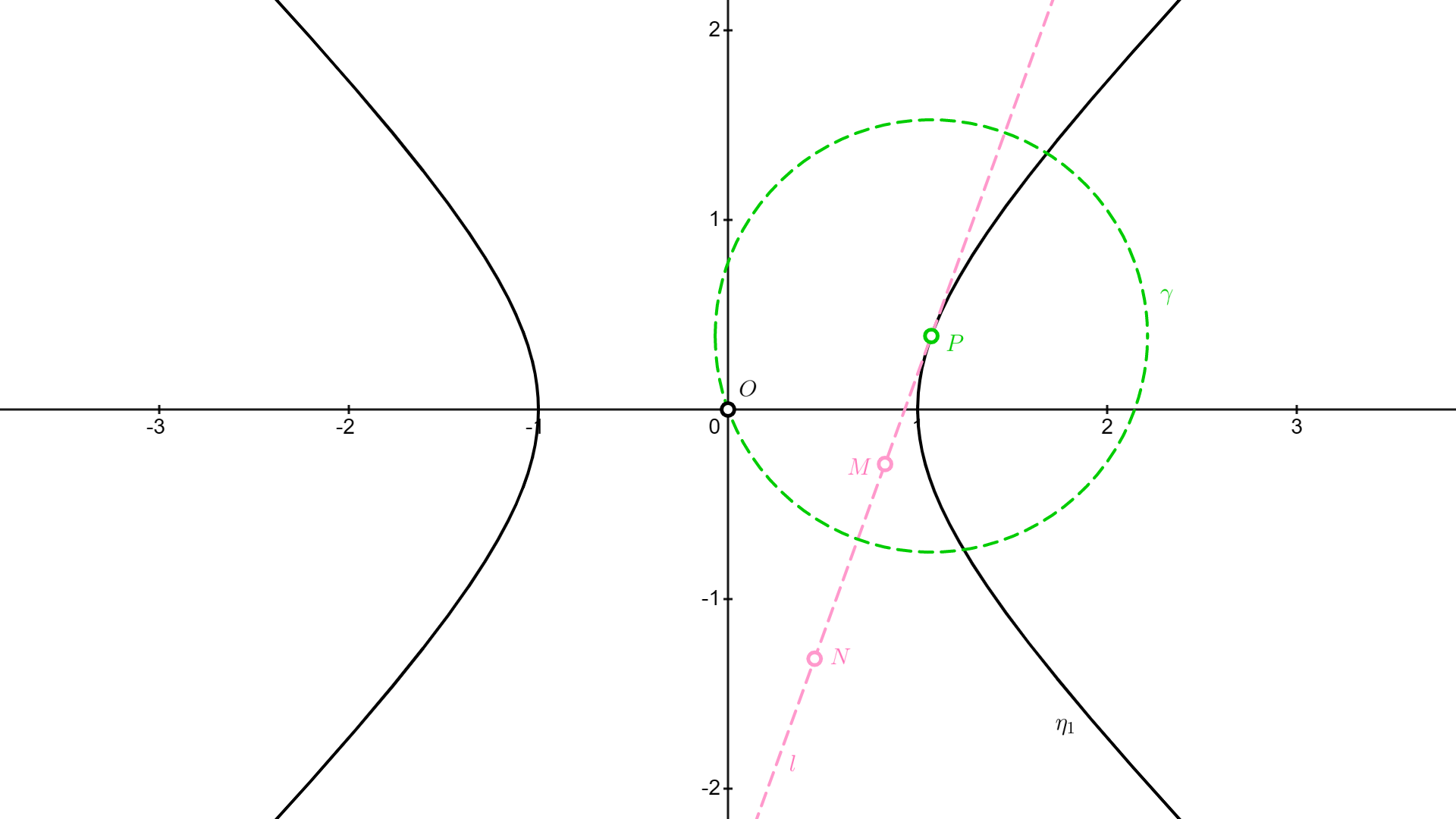 ▲意外にもシンプルな滑り出し
▲意外にもシンプルな滑り出し 中心が点$P$で原点$O=(0,0)$を通る円$\gamma$を用意します。$\gamma$の式は以下の通りですね。
$$ \gamma:\,\left(x-\frac{1}{\cos\left(p\right)}\right)^{2}+\left(y-\tan\left(p\right)\right)^{2}=\frac{1}{\cos^{2}\left(p\right)}+\tan^{2}\left(p\right)$$
いま、簡単な計算により、線分$PM$の長さは$\displaystyle k\sqrt{\frac{1}{\cos^{2}\left(p\right)}+\tan^{2}\left(p\right)}$、線分$PN$の長さは$\displaystyle \frac{1}{k}\sqrt{\frac{1}{\cos^{2}\left(p\right)}+\tan^{2}\left(p\right)}$であるとわかります。すなわち$\displaystyle PM\times PN=\frac{1}{\cos^{2}\left(p\right)}+\tan^{2}\left(p\right)$が成り立ちます。$k$と$\displaystyle \frac{1}{k}$の符号が一致することから、この事実は$N={\rm inv}(M , \gamma)$と言い換えられます。円$\gamma$を登場させたのはこれが目的です。
2つの双曲線を追加しよう
さて、$x_1,y_1,x_2,y_2$に注目すると、以下の関係は明らかです。
$$ \left\{
\begin{eqnarray}
\displaystyle x_{1}^{\ 2}-y_{1}^{\ 2}-1&=&-k^{2} \\[6pt]
\displaystyle x_{2}^{\ 2}-y_{2}^{\ 2}-1&=&-\frac{1}{k^{2}} \\[6pt]
\displaystyle \frac{x_{1}y_{1}}{k^{2}}&=&x_{2}y_{2}
\end{eqnarray}
\right.$$
ここで任意の実数$t$をとり、$\varPsi$および$u$を
$$ \left\{
\begin{eqnarray}
\varPsi &=&\cos\left(2t\right)\left(\left(x_{1}^{\ 2}-y_{1}^{\ 2}-1\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)-1\right)+2\sin\left(2t\right)\left(x_{1}y_{1}\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)+x_{2}y_{2}\right) \\[6pt]
u&=&\cos\left(2t\right)\left(x_{1}^{\ 2}-y_{1}^{\ 2}\right)+2\sin\left(2t\right)x_{1}y_{1}\quad \dots({\rm i})
\end{eqnarray}
\right.$$と定義してみましょう。
……既にお気付きのことと拝察しますが、どう見ても$\varPsi =0$ですね。とはいえそれで終わってしまうのも面白くないので、ついでに定義しておいた$u$を使って$\varPsi$を表してみます。気合で計算すると
$$ \begin{align}
\varPsi &=\cos\left(2t\right)\left(\left(x_{1}^{\ 2}-y_{1}^{\ 2}-1\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)-1\right)+2\sin\left(2t\right)\left(x_{1}y_{1}\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)+x_{2}y_{2}\right) \\[6pt]
&=\left(\cos\left(2t\right)\left(x_{1}^{\ 2}-y_{1}^{\ 2}-1\right)+2\sin\left(2t\right)x_{1}y_{1}\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)+2\sin\left(2t\right)x_{2}y_{2}-\cos\left(2t\right) \\[6pt]
&=\left(u-\cos\left(2t\right)\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}-1\right)+2\sin\left(2t\right)x_{2}y_{2}-\cos\left(2t\right) \\[6pt]
&=\left(u-\cos\left(2t\right)\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}\right)+2\sin\left(2t\right)x_{2}y_{2}-u
\end{align}$$
となるので、$\varPsi =0$より$\left(u-\cos\left(2t\right)\right)\left(x_{2}^{\ 2}-y_{2}^{\ 2}\right)+2\sin\left(2t\right)x_{2}y_{2}=u$$\quad \dots({\rm ii})$を導けます。
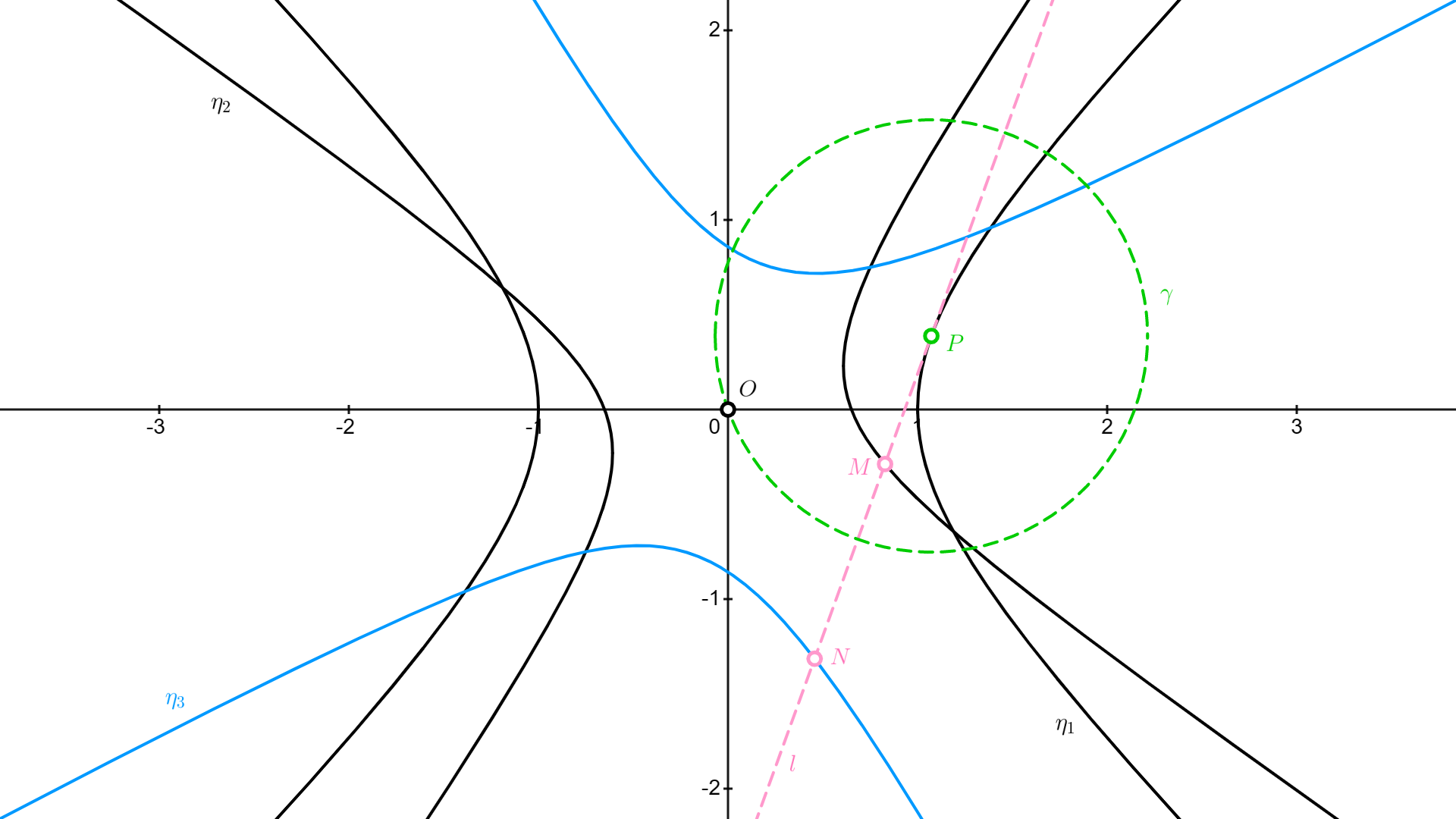 ▲我ながらどうやって$\varPsi$を思いついたのでしょう
▲我ながらどうやって$\varPsi$を思いついたのでしょう 先の段落では$\varPsi$やら$u$やら謎めいた文字が古文書並みに頻出していましたが、どうにかしてこれらをレムニスケートと関連づけられないものでしょうか。色々試行錯誤してみると、$({\rm i})$を
$$ \begin{align}
u&=\cos\left(2t\right)\left(x_{1}^{\ 2}-y_{1}^{\ 2}\right)+2\sin\left(2t\right)x_{1}y_{1} \\[6pt]
&=\left(\cos^{2}\left(t\right)-\sin^{2}\left(t\right)\right)\left(x_{1}^{\ 2}-y_{1}^{\ 2}\right)+4\sin\left(t\right)\cos\left(t\right)x_{1}y_{1} \\[6pt]
&=\left(x_{1}\cos\left(t\right)+y_{1}\sin\left(t\right)\right)^{2}-\left(-x_{1}\sin\left(t\right)+y_{1}\cos\left(t\right)\right)^{2}
\end{align}$$
と変形できることに思い至ります。したがって、原点$O$を中心として、直角な双曲線$x^2-y^2=u$を角度$t$だけ回転させた双曲線$\eta_2$を用意してあげれば、点$M$が$\eta_2$上に乗ると言えますね($\because$ $\eta_2$の式が$\left(x\cos\left(t\right)+y\sin\left(t\right)\right)^{2}-\left(-x\sin\left(t\right)+y\cos\left(t\right)\right)^{2}=u$となるため)。直角な双曲線とレムニスケートは反転で互いに移りあうので(有名事実)、かなり有用な手がかりと考えられます。
ところで、点$M$の定義より$\eta_2$は($l$と共有点をもつ範囲内で)任意の角度・大きさになりえます。この任意性もあとで使うため、頭の片隅に入れておきましょう。
類推から、$({\rm ii})$の式も「何らかの直角な双曲線上に点$N$が乗る」と示唆しているように見えてきます。この直感をもとに$({\rm ii})$を整理していくと、
$$ \tan\left( 2v\right)=\frac{\sin\left(2t\right)}{u-\cos\left(2t\right)}$$
をみたす実数$v$(2通りの値が考えられますが、そのうちの片方)を用いて、$({\rm ii})$は
$$ \left(x\cos\left(v\right)+y\sin\left(v\right)\right)^{2}-\left(-x\sin\left(v\right)+y\cos\left(v\right)\right)^{2}=\frac{u}{\sqrt{u^{2}-2u\cos\left(2t\right)+1}}$$
と表せます。行間の広さがパンゲア大陸級ですね。反省します。
何はともあれ、この変形によって判明することがあります。つまり、直角な双曲線$\displaystyle x^2-y^2=\frac{u}{\sqrt{u^{2}-2u\cos\left(2t\right)+1}}$を角度$v$だけ回転させた双曲線$\eta_3$について、点$N$が$\eta_3$上に乗るわけです。
反転してレムニスケートの世界へ
現状を整理します。中心を共有する3つの直角な双曲線$\eta_1, \eta_2, \eta_3$があり、$\eta_2$上の点$M$は円$\gamma$に関する反転によって$\eta_3$上の点$N$に移ります。また、2点$M, N$はいずれも$\eta_1$の特定の接線上に乗っています。
そうですね。『三平方の定理』のときと同じ状況です。要するに、ここまでで登場した全オブジェクト(双曲線、円、直線など)を、中心が$O$、半径が$1$の円(この円を$\delta$とします)で反転すれば一気に話が進みます。というわけで直ちに反転しましょう。Inverse the universe.
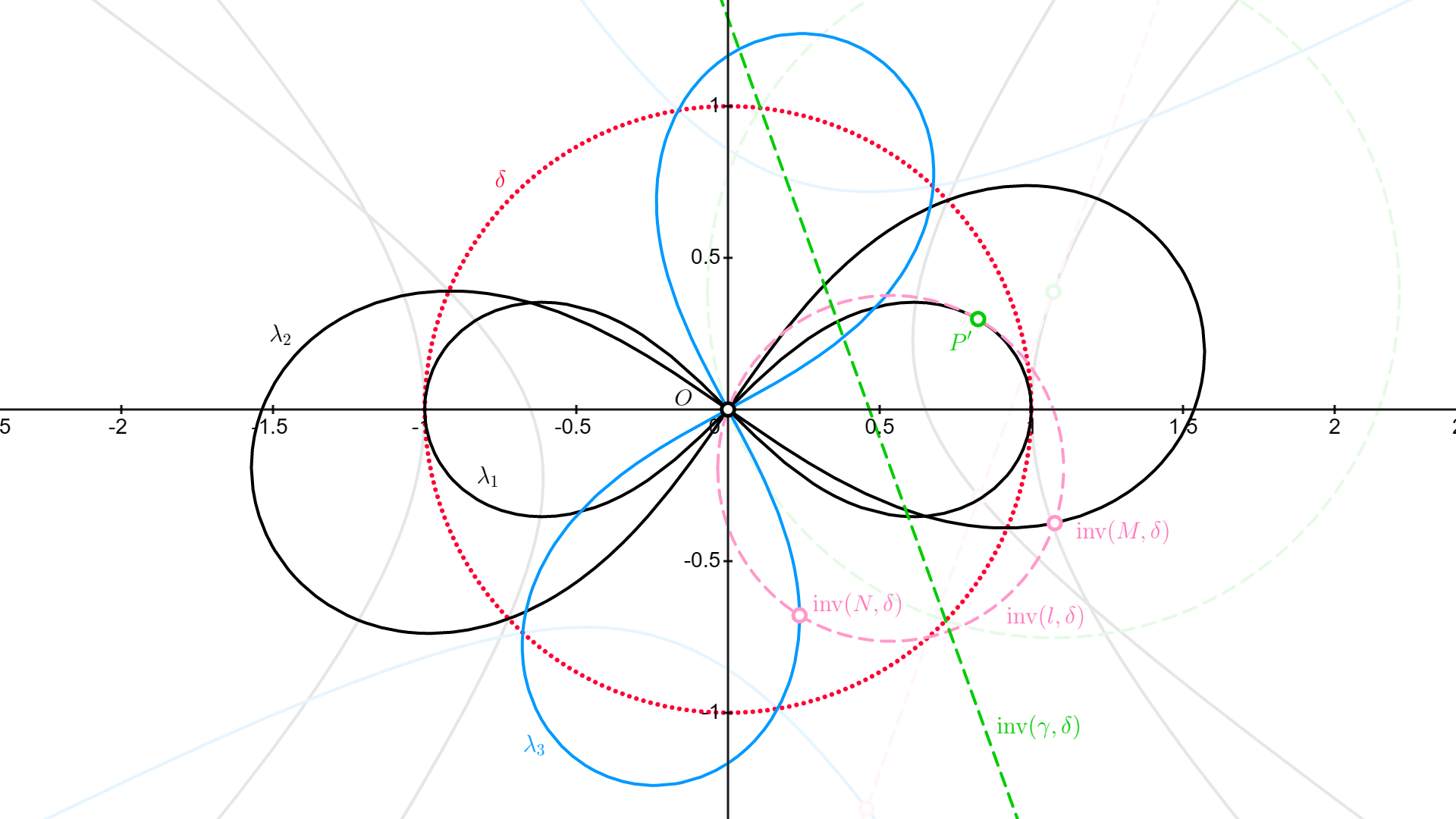 ▲見た目の不穏さが凄まじいです
▲見た目の不穏さが凄まじいです $\lambda_x ={\rm inv}(\eta_x , \delta) \quad (x=1,2,3)$とすると、$\lambda_1, \lambda_2, \lambda_3$はいずれも点$O$を中心としたレムニスケートになります。$P'={\rm inv}(P , \delta)$と定めれば、
前回の記事
の補題5より、${\rm inv}(M , \delta)$と${\rm inv}(N , \delta)$は線分$OP'$の垂直二等分線${\rm inv}(\gamma , \delta)$に関して対称な位置にあるとわかります。
ゆえに、${\rm inv}(\gamma , \delta)$に関する$\lambda_3$の対称移動で得られるレムニスケート${\lambda_3}'$を考えると、${\rm inv}(M , \delta)$は${\lambda_3}'$上に乗ることになります($\because$ ${\rm inv}(N , \delta)$が$\lambda_3$上に存在するため)。
いま、点$M$は$\eta_2$と$l$の交点の1つでした。一般に、直線と双曲線が交わっているとき、交点の数は2つです。それでは、もう1つの交点についても考えてみたくなりますよね。
こちらの交点$R=(x_3,y_3)$の座標を
$$ \left(x_{3},y_{3}\right)=\left(\tan\left(p\right)j+\frac{1}{\cos\left(p\right)},\,\frac{j}{\cos\left(p\right)}+\tan\left(p\right)\right)$$
とおいて($j$は実数)、
$$ S=\left(x_{4},y_{4}\right)=\left(\frac{\tan\left(p\right)}{j}+\frac{1}{\cos\left(p\right)},\,\frac{1}{j\cos\left(p\right)}+\tan\left(p\right)\right)$$
という点$S$を定めれば、あれがああなってこれがこうなって……………………、もう良いですね。$k$が$j$になっただけなので、$k$のときの議論が同様に回ります。$(x_3,y_3)$もまた$\eta_2$上の点ですから、$\cos\left(2t\right)\left(x_{3}^{\ 2}-y_{3}^{\ 2}\right)+2\sin\left(2t\right)x_{3}y_{3}=u$が成り立って、
$$ \left(u-\cos\left(2t\right)\right)\left(x_{4}^{\ 2}-y_{4}^{\ 2}\right)+2\sin\left(2t\right)x_{4}y_{4}=u$$
も従います。その後も同様に計算して、$\eta_2$と$l$の2つの交点はいずれも${\lambda_3}'$上に乗ります。
 ▲ねえみてみてこれねえこれ(語彙力消失)
▲ねえみてみてこれねえこれ(語彙力消失)「任意」という語彙の素晴らしさ
${\rm inv}(l , \delta)$は原点$O$を通り点$P'$で$\lambda_1$に接する円です。よって、$\lambda_1,\lambda_2,{\lambda_3}'$について『余弦定理』の成立を確認すれば、適当な拡大縮小によりもとの定理を証明できます($\because$ $\lambda_2$が任意の角度・径をとりうることを確認すればよいですが、先述した$\eta_2$の任意性より確かめられます)。
$\eta_1,\eta_2,\eta_3$の式に注目すると、これらの相似比は
$$ \begin{align}
\eta_1 : \eta_2 : \eta_3
&= \sqrt{1}:\sqrt{u}:\sqrt{\frac{u}{\sqrt{u^{2}-2u\cos\left(2t\right)+1}}} \\[6pt]
&= \frac{1}{\sqrt{u}}:1:\frac{1}{\sqrt[4]{u^{2}-2u\cos\left(2t\right)+1}}
\end{align}$$
となっています。よって、これらを反転した$\lambda_1,\lambda_2,\lambda_3$の相似比は
$$ \begin{align}
\lambda_1 : \lambda_2 : \lambda_3
&= \sqrt{u}:1:\sqrt[4]{u^{2}-2u\cos\left(2t\right)+1}
\end{align}$$
ですね。$\lambda_3$と${\lambda_3}'$は合同なので、結局3つのレムニスケートにおける周長の比は$\displaystyle \sqrt{u}:1:\sqrt[4]{u^{2}-2u\cos\left(2t\right)+1}$だったのです。
この組について『余弦定理』の成立は自明であり、証明の全編を統合して定理が証明されました。やっと終わった。 $\blacksquare$
応用
前回は汎用性が絶無であることを嘆くにとどまりましたが、今回は少しだけ汎用性を主張できそうです。ここでは3つの系を紹介しますね。
点$O$を中心とするレムニスケート$L_1,L_2$が$45^{\circ}$の角度で交わっている。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点が2つできるとき、それを$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1,L_2,L_3$の周長をそれぞれ$a,b,c$とすると、$a^4+b^4=c^4$ が成立する。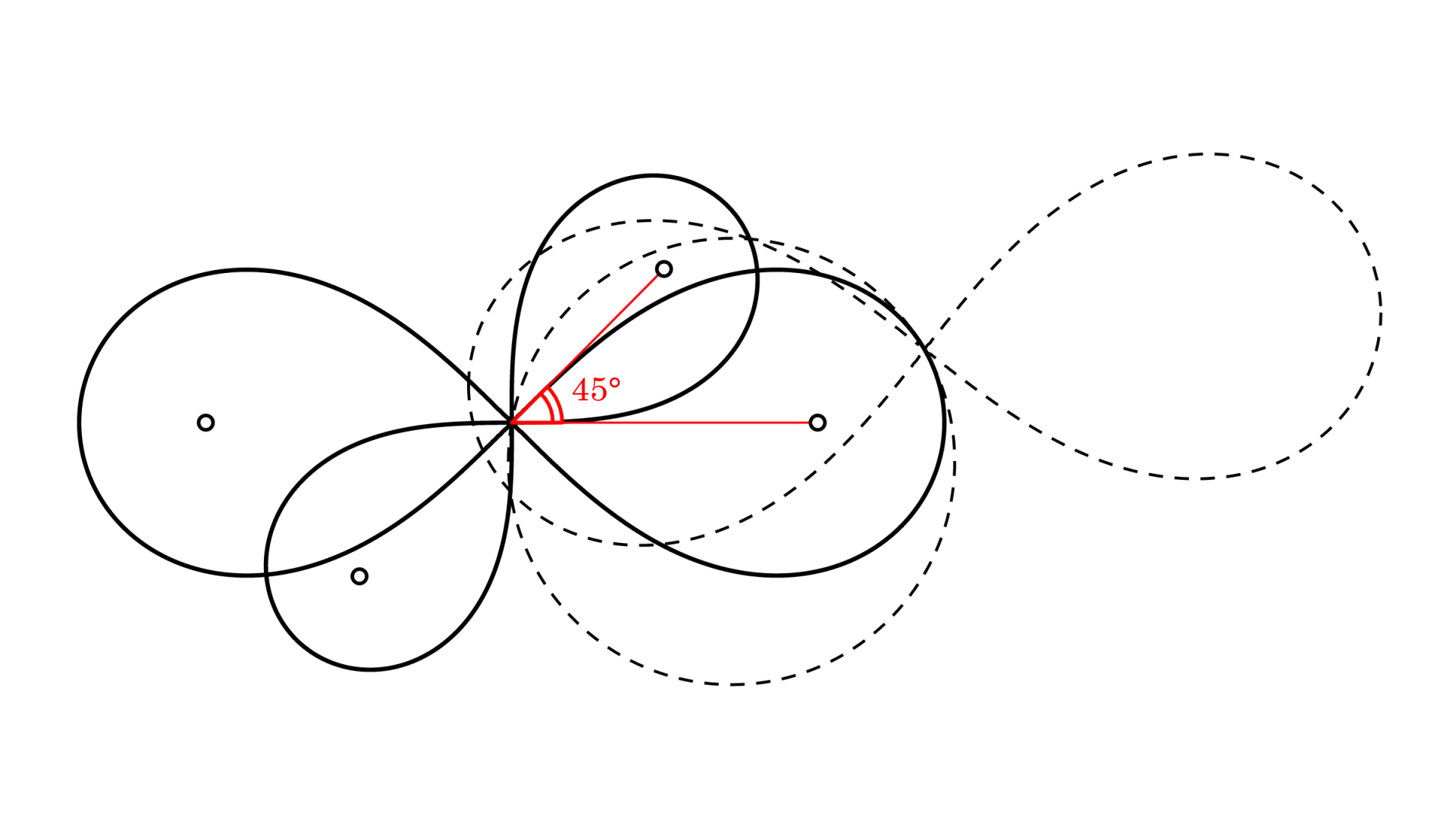
▲数学的にはこちらが『三平方』だったのかもしれません
点$O$を中心とするレムニスケート$L_1,L_2$があり、$L_2$の長軸の端点はいずれも$L_1$上に乗っている。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点が2つできるとき、それを$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1,L_2,L_3$の周長をそれぞれ$a,b,c$とすると、$a^4-b^4=c^4$ が成立する。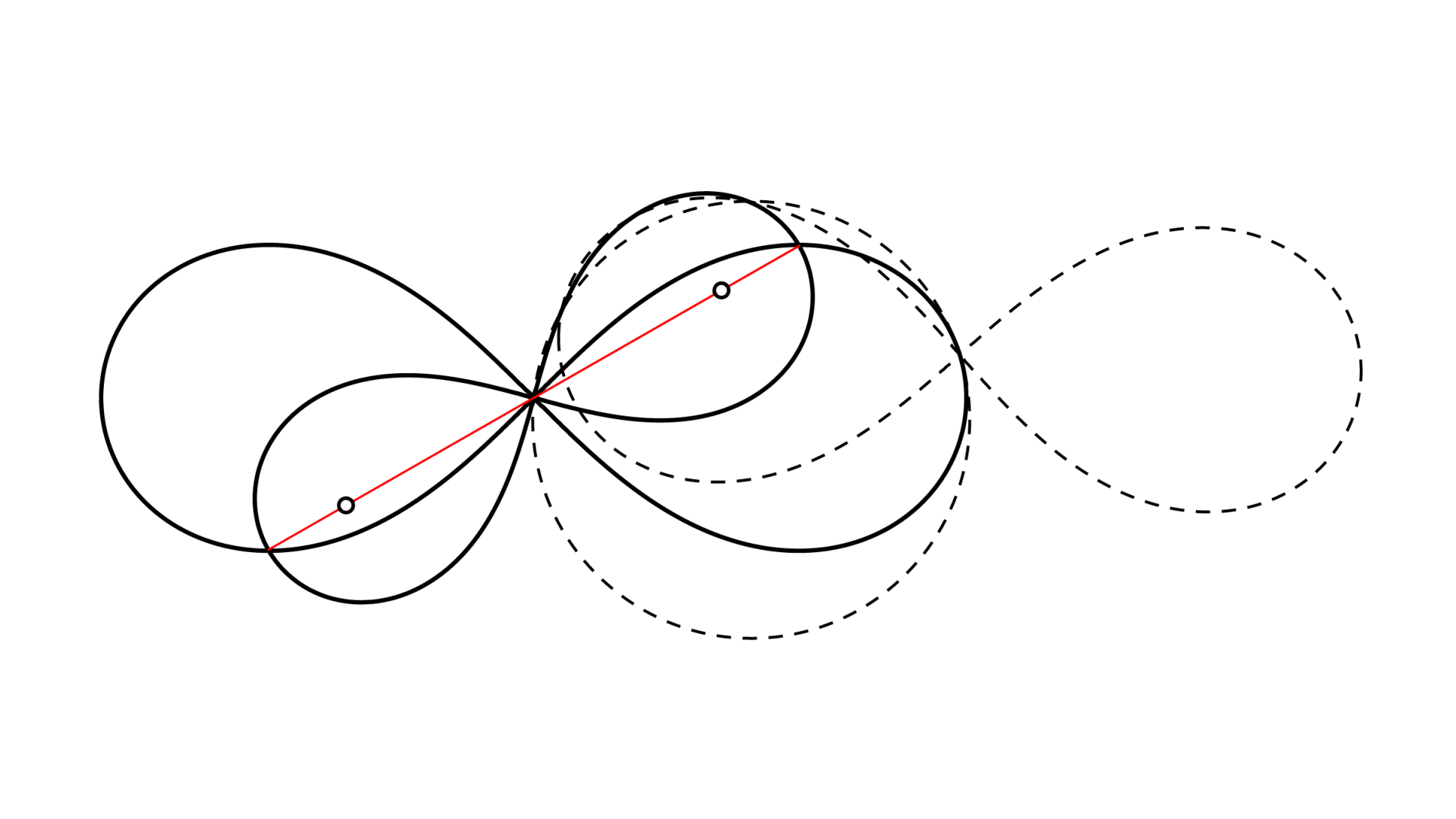
▲$b=a\sqrt{\cos ( 2\theta )}$から従います
点$O$を中心とするレムニスケート$L_1,L_2$があり、$L_2$の焦点はいずれも$L_1$上に乗っている。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点が2つできるとき、それを$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1$と$L_3$は合同である 。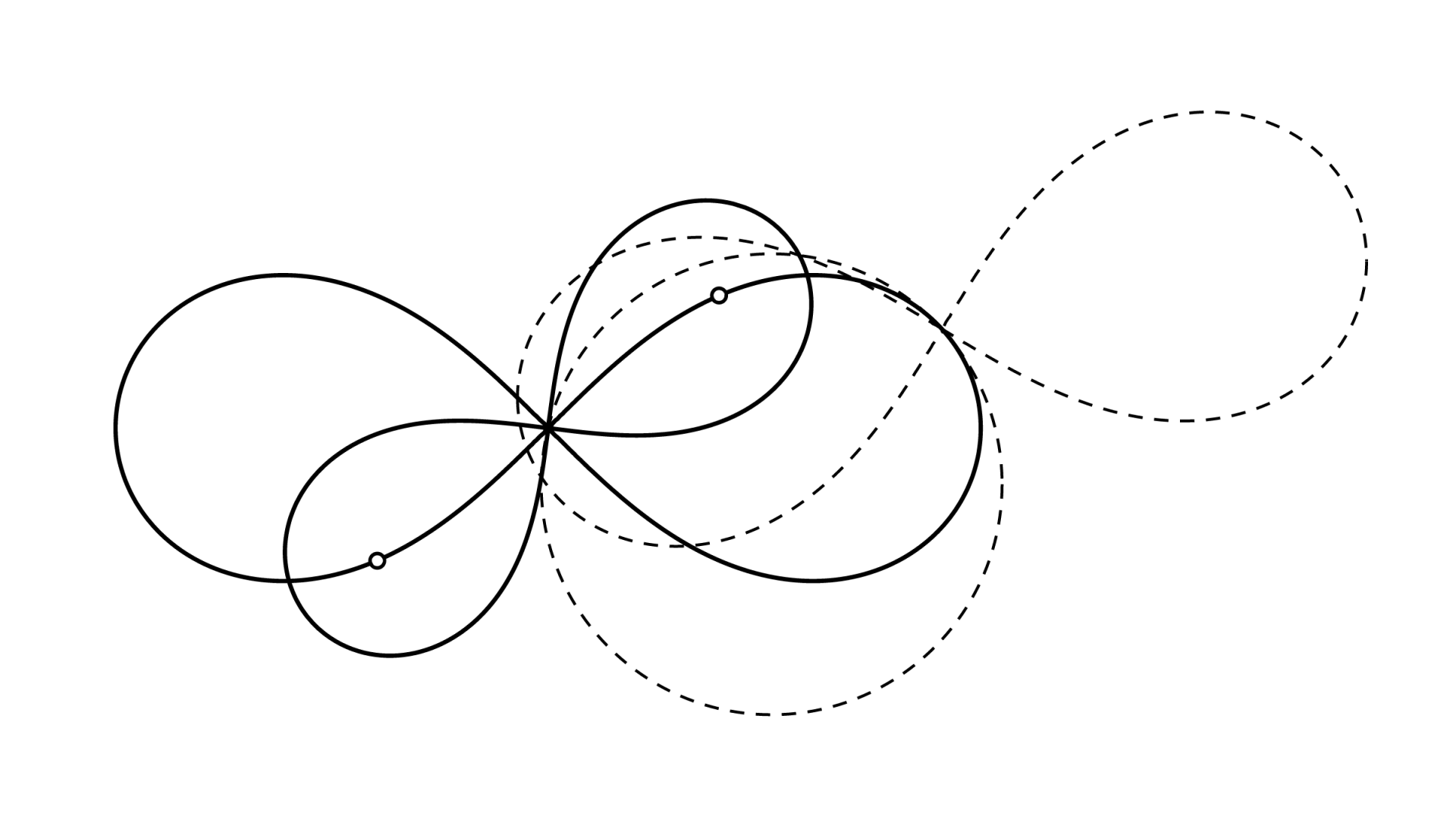
▲きれい(突然の自画自賛)
読者の皆様が具有する莫大かつ精緻な数学力に信頼を寄せて、系の証明は省略します。「他にもこういった応用が利くよ!」という情報をお持ちの方はコメントでご教示ください。
結語
 ▲点線で描かれたレムニスケートはすべて同じ大きさです
▲点線で描かれたレムニスケートはすべて同じ大きさです私がレムニスケートを研究対象としてから、ちょうど1年になります。日本語の論文が殆ど無い分野で、初めは英語の濁流に呑まれ右往左往していましたが、少しは有用な結果を残せたでしょうか。私自身の見解としては、数学よりもむしろ物理の領域で使い道を見つけられそうに感じていますが……。
ところで、本記事の執筆中に、
レチセン
氏が奇しくも『
余弦定理の四面体ver.
』という記事を投稿なさっていました。余弦定理を2次元から3次元に拡張されたわけですね。そして私の記事では余弦定理を三角形からレムニスケートに拡張しています。
すると、2つの記事を合わせて、「3次元におけるレムニスケート的なもの」に余弦定理を拡張できる可能性も考えられますね。未だ予想さえ立てられていない段階ですが、果たしてどうなることやら。
話題は尽きませんが、この辺りで記事を締め括ります。
最後までお読みいただき、ありがとうございました。感想・指摘・先行研究の紹介・これから高騰する株の紹介などはコメントまで。あと誰か定理を使ってください。ちなみに、用紙サイズA3の倍率85%で本記事を印刷すると綺麗に刷れます。
追記 (2023/05/08)
記事投稿時点では見逃していましたが、なんとレムニスケート版『余弦定理』は以下と同値になります。
図で、白い点はレムニスケートの焦点である。このとき、$x \times y = z^2$ が成立する。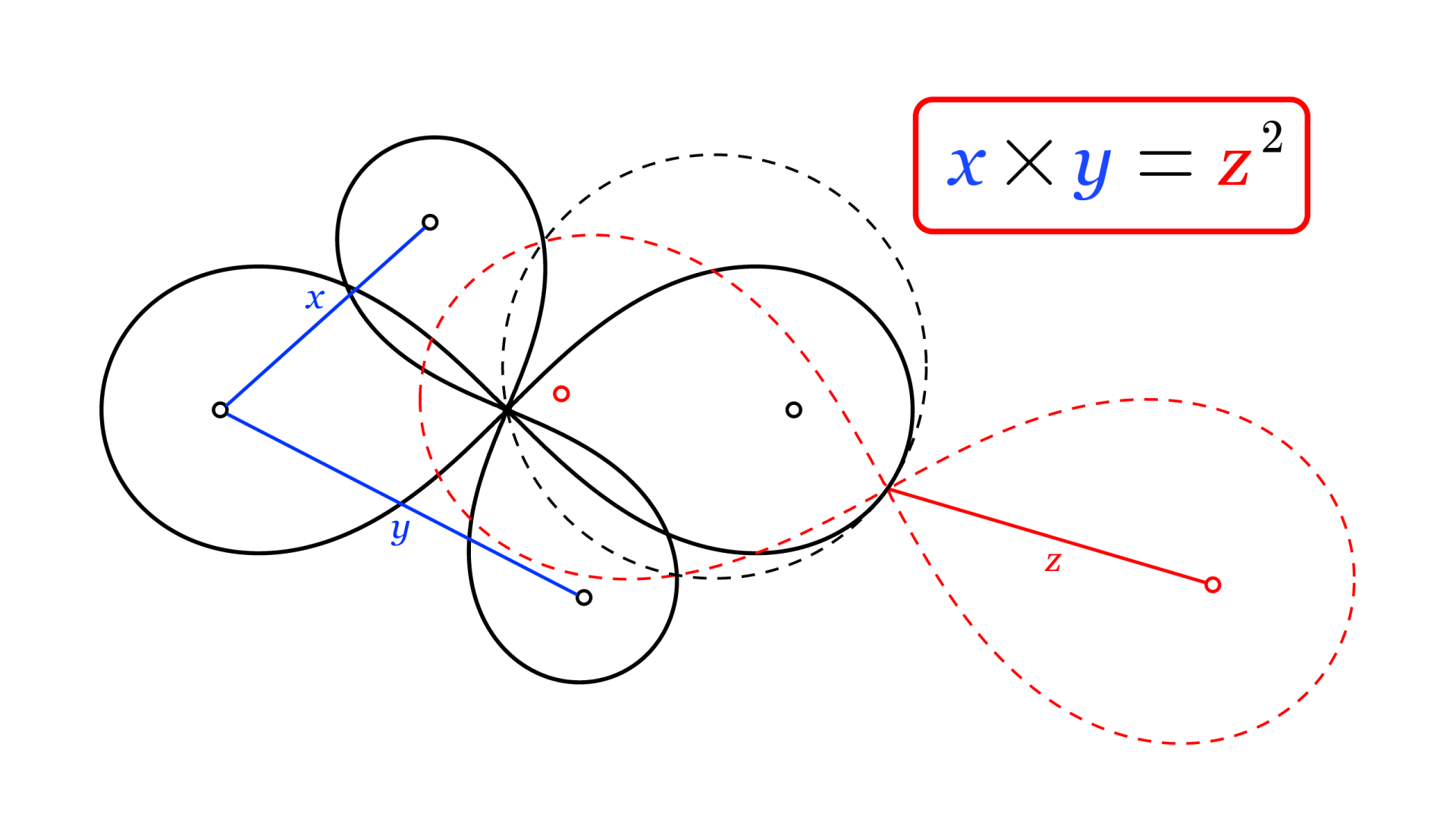
▲幻聴が教えてくれました
断然こちらのほうがエレガントですね。どうして記事投稿前に気づけなかったのでしょう……。
 ▲レムニスケートは最強だった(個人の感想です)
▲レムニスケートは最強だった(個人の感想です)