3つのレムニスケートが生み出す『a^2+b^2=c^2』について - New Pythagorean-like theorem in lemniscate geometry -
長いので、忙しい人はあとがきだけ読みましょう。興味と余暇が湧いたら読み直す、それがよいです。
匿(Tock)である。まずは先日公開した記事、【
レムニスケートと1本の直線が生み出す関係について - A relationship between a line and a lemniscate -
】が当アカウント初の高評価数2ケタに到達したことについて感謝を申し上げる。どこにでもいる普通の暇人が書いた記事がここまで注目されるのは、私自身としても予想外であった。ありがたい。
今回は幾何学を嗜むうえで欠かせない重要な定理、『三平方の定理』に関する記事となる。$a^2+b^2=c^2$で知られる、あの定理である。まあ、三平方の定理を知らない人からすれば、「どの定理だ?」と感じるであろうが。
とはいえ、私のMathlog記事を読む方々は基本的に偏差値が高い。それゆえ、正直なところ「流石に知っている、我々を無知蒙昧と見下すつもりなのか」と非難されそうにも感じる。ごく一部の方に需要があるかもしれない、と、一縷の希望を糧に筆を進める次第である。メンタルは強く保つ。
……タイトルと目次で色々察した方もいらっしゃることであろう。はい、今回も独自研究を詰め込みました。「非常に気持ち悪い」(Twitterで相互フォローの
立見鶏
氏談。氏は本記事の共同研究者です。……あれ? 先程独自研究とか書いてあったような……?)構図が登場するので、是非最後までお読みください。
特に理由はないが、普段のオリジナル書式ではなく、Mathlog標準の書式を使って本記事を書いている。そのため、ここ10分くらいずっと「行間狭いな?」と言い続けているらしい。どちらの書式が読みやすいか、コメント等で教えていただきたい。次回以降の記事に反映する。
三平方の定理とは?
現行の
学習指導要領
によれば、日本人は中学3年生で三平方の定理を履修するとされる。要するに義務教育の範囲内であり、数学領域における他の定理と比較しても、三平方の定理が卓越した汎用性および性質自体の単純さを具有していることが伺える。仮に性質が複雑であれば、三角関数の加法定理のように義務教育範囲外となっていたはずだ。
では、その『三平方の定理』とはどのようなものか。多くの文献で紹介されているが、今一度ここに掲示しよう。
$\angle C=90^{\circ}$である直角三角形$ABC$について、辺$BC,CA,AB$の長さをそれぞれ$a,b,c$とすると$a^2+b^2=c^2$が成立する。
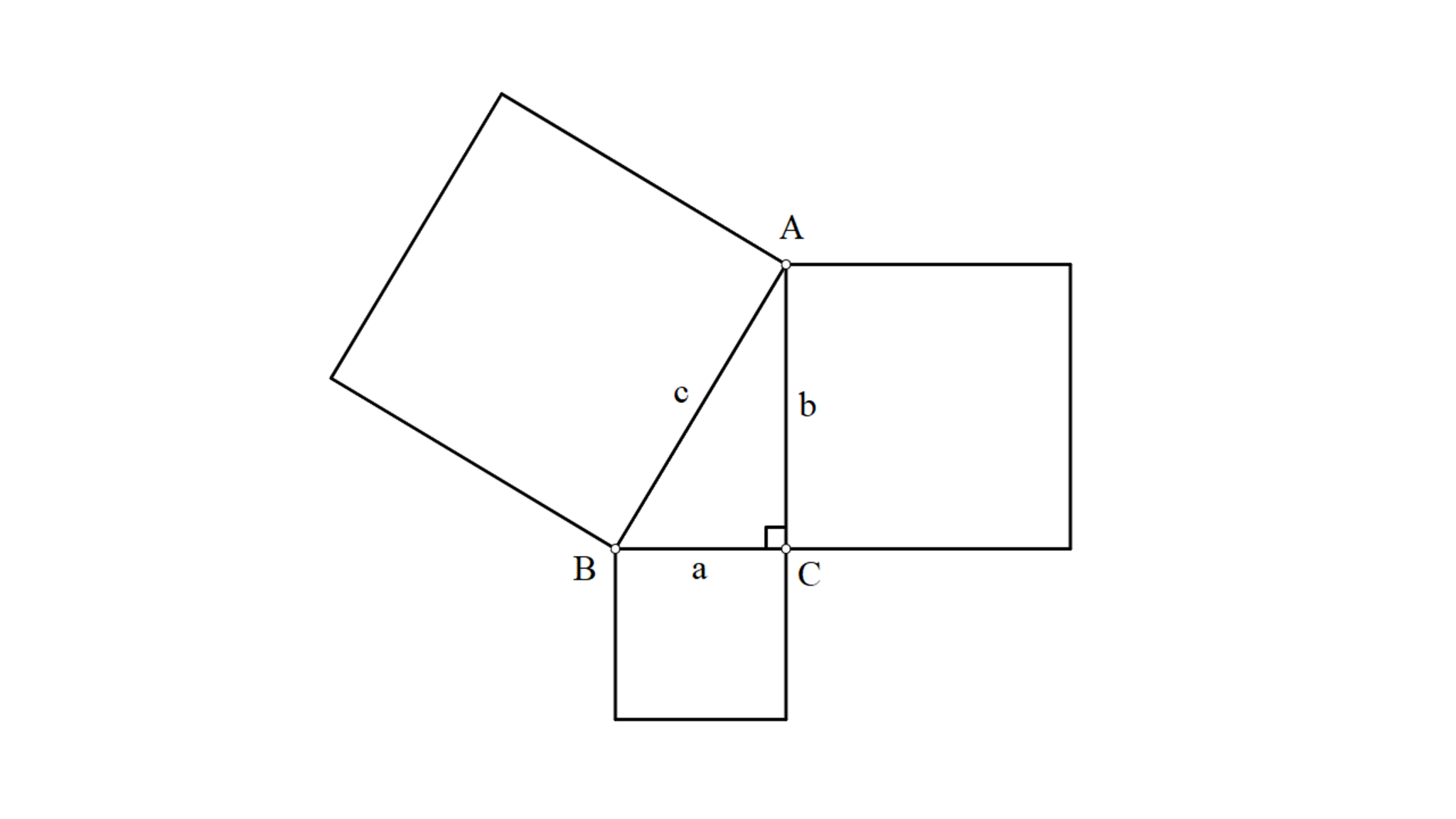 中学校の教科書を読み返してみよう
中学校の教科書を読み返してみよう
有名な定理である。この定理によると、例えば$\angle C=90^{\circ},$$BC=3,$$CA=4$の直角三角形$ABC$において、$AB=\sqrt{\displaystyle 3^2+4^2}=5$となる。こちらも有名な比、$3:4:5$である。
古代ギリシアにいた数学者ピタゴラス(紀元前582年~紀元前496年)が本定理について詳細な研究を行ったとされ、彼の名を借りてピタゴラスの定理と呼ばれることもある。なお、英語圏ではこちら寄りの"Pythagorean Theorem"という呼び方が主流であり(意外にも「ピタゴラスの」という意味の形容詞Pythagoreanが存在する)、三平方の定理は日本独自の呼称とのこと。
ただし、ピタゴラス以前の古バビロニア王国時代の遺跡から本定理と関連した内容が著された粘土板も見つかっており、現在「三平方の定理を最初に発見したのはピタゴラスである」という主張は一般的でないようだ。
……話題が歴史方面に逸れつつあるが、取り敢えず、三平方の定理を証明してみよう。
三平方の定理の証明
2000年以上の歴史の中で、三平方の定理に対する無数の証明が見つかっているとされる。参考文献にも挙げている
Pythagorean Theorem and its many proofs
には、本記事公開時点で122パターンの証明が載っている。
ここでは、個人的にお気に入りの証明(先程のサイトの56番目のパターンに含まれるらしい。
このパターン
は独特で、ある図をもとに4864種類もの証明を構成している)を1つ紹介したい。
$\angle A$の二等分線を軸として$\triangle ABC$を対称移動させ、2点$B,C$が移る点をそれぞれ$B',C'$とする。このとき、明らかに$B',C'$はそれぞれ直線$AC,AB$上に乗る。
$BC$と$B'C'$の交点を$D$とすると$\triangle ABC \sim \triangle DBC' \equiv \triangle DB'C$であるから(それぞれの角度と対称性に注目すれば判る)、相似比より$BD=\dfrac{c(c-b)}{a},$$CD=\dfrac{b(c-b)}{a}$となる。
いま、$BD+CD=BC$なので$\dfrac{c(c-b)}{a}+\dfrac{b(c-b)}{a}=a$となり、これを整理すれば$a^2+b^2=c^2$が得られる。 (証明終)
 大抵のことはゴリゴリと計算すれば解決する
大抵のことはゴリゴリと計算すれば解決する
別に綺麗な証明ではないのだが、どうして気に入っているのか。それはこの証明が、「小学生時代の私が文献を読むことなく自力で三平方の定理を証明したときの手順」だからである。至極どうでもよい。
ちなみに、三平方の定理は逆も成立する。すなわち、$a^2+b^2=c^2$ならば、3辺の長さがそれぞれ$a,b,c$である三角形が直角三角形となる。こちらの証明は省く。
三平方の定理をみたす自然数の組
先程の$(a,b,c)=(3,4,5)$のように、方程式$a^2+b^2=c^2$は自然数解を有する。このような自然数解は無限に存在し、一例を挙げると
$$ (a,b,c)=(2k+1, 2k^2+2k, 2k^2+2k+1)$$
は任意の自然数$k$について$a^2+b^2=c^2$をみたす。実際、$(2k+1)^2+\left(2k^2+2k\right)^2$$=4k^4+8k^3+8k^2+4k+1$$=\left(2k^2+2k+1\right)^2$が成り立っている。$k=1$を代入すると$(a,b,c)=(3,4,5)$となり、初めに挙げた$3:4:5$の比が出てくる。
なお、どのような自然数解$(a,b,c)$についても、$abc$は$60$の倍数となることが知られている。これは整数論の話になるので、証明は割愛し、読者への演習問題とする。人生で一度は言っておきたいフレーズ。
三角関数$\sin\theta,\cos\theta$を用いた定式化
高校1年生になると三角関数が登場する(厳密には三角比が登場するのだが、ここでは特に区別しない)。所謂「サイン・コサイン・タンジェント」である。
これらは以下のように定義されている。一般的な定義とは異なるが、今後の議論のために敢えてこの表現を用いた。
$xy$座標平面の第1象限上で、2点$O(0,0),A(1,0)$を直径とする半円$\gamma$を描く。$\gamma$上の点$B$について、弧$OB$の長さが$\theta$であるときの弦$OB$の長さを$\sin \theta$、弧$AB$の長さが$\theta$であるときの弦$OB$の長さを$\cos \theta$と表す。
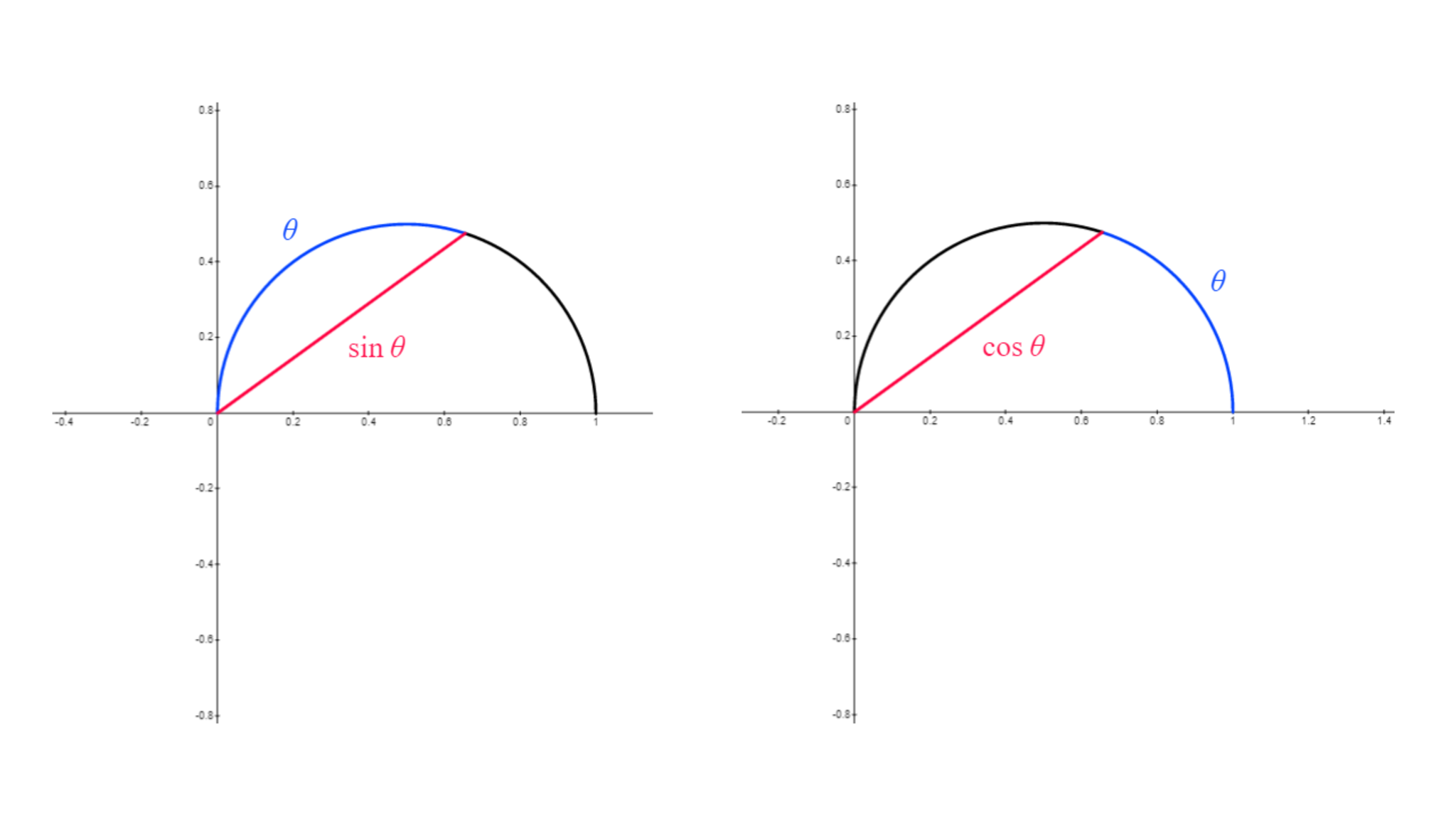 かなり風変わりな定義の仕方である
かなり風変わりな定義の仕方である
このように定義すると、以下の定理が成立する。
$\sin^2 \theta+\cos^2 \theta=1$ (ただし、$\sin^2 \theta=(\sin \theta)^2,$$\cos^2 \theta=(\cos \theta)^2$を表す)
定義1の円$\gamma$および点$O,A,B$をそのまま流用する。
点$B$から引いた$x$軸の平行線と$\gamma$との交点のうち$B$でないものを$B'$とすると、弧$AB'$の長さは$\theta$である。よって弦$OB'$の長さは$\cos \theta$となり、対称性から(弦$OB'$の長さ)$=$(弦$AB$の長さ)であることを踏まえると、$\triangle OAB$は$OA=1,$$OB=\sin \theta,$$AB=\cos \theta$の三角形と判る。
円周角の定理(もしくはタレスの定理)から$\angle OBA=90^{\circ}$が従うので、定理1により$OB^2+AB^2=OA^2$、すなわち$\sin^2 \theta+\cos^2 \theta=1$が示された。 (証明終)
見方を変えれば、定理2は三平方の定理そのものということもできる。つまり、斜辺の長さが$1$である直角三角形において、残る2辺の長さは(適当な$\theta$を用いて)必ず$\sin\theta,\cos\theta$と表せるのだ。先述の$3:4:5$の比で考えてみると、$\sin\theta=0.6,$$\cos\theta=0.8$となるような$\theta$が存在する、といえる(大体$\theta\approx{36.8699}^{\circ}$で$\sin\theta=0.6,$$\cos\theta=0.8$が実現する)。
レムニスケート関数${\rm sl\,}\theta,{\rm cl\,}\theta$の導入
ここまで読めば、三平方の定理がどのようなものであるか、多くの読者が理解できたことと思われる。そしてこのあたりで、「三平方の定理を拡張できないかな?」と考えるのも、幾何学を嗜むものとしてごく自然なことだ。実際、高校数学では三平方の定理から派生して余弦定理が導かれ、我々の根源にある拡張欲求を充たしてくれる。
だが、本記事の執筆者は他でもない、過去に3連続でレムニスケート関連の記事を投稿した匿である。これが何を意味するか。
そう。円を用いて定義した三角関数を、レムニスケートへ拡張するのだ。口を開けばレムニスケートなのだ。……具体的には、以下のように拡張する。「レムニスケートって何?」という方は過去の記事、【
オリジナル図形問題 with 円 and 楕円 and レムニスケート
】のイントロダクションあたりを読んでおくこと。
$xy$座標平面に2点$O(0,0),A(1,0)$をとり、「$O$を中心とし$A$で$x$軸と直交するレムニスケート」のうち、第1象限に含まれる部分を$\lambda$とする。$\lambda$上の点$B$について、弧$OB$の長さが$\theta$であるときの弦$OB$の長さを${\rm sl\,} \theta$、弧$AB$の長さが$\theta$であるときの弦$OB$の長さを${\rm cl\,} \theta$と表す。
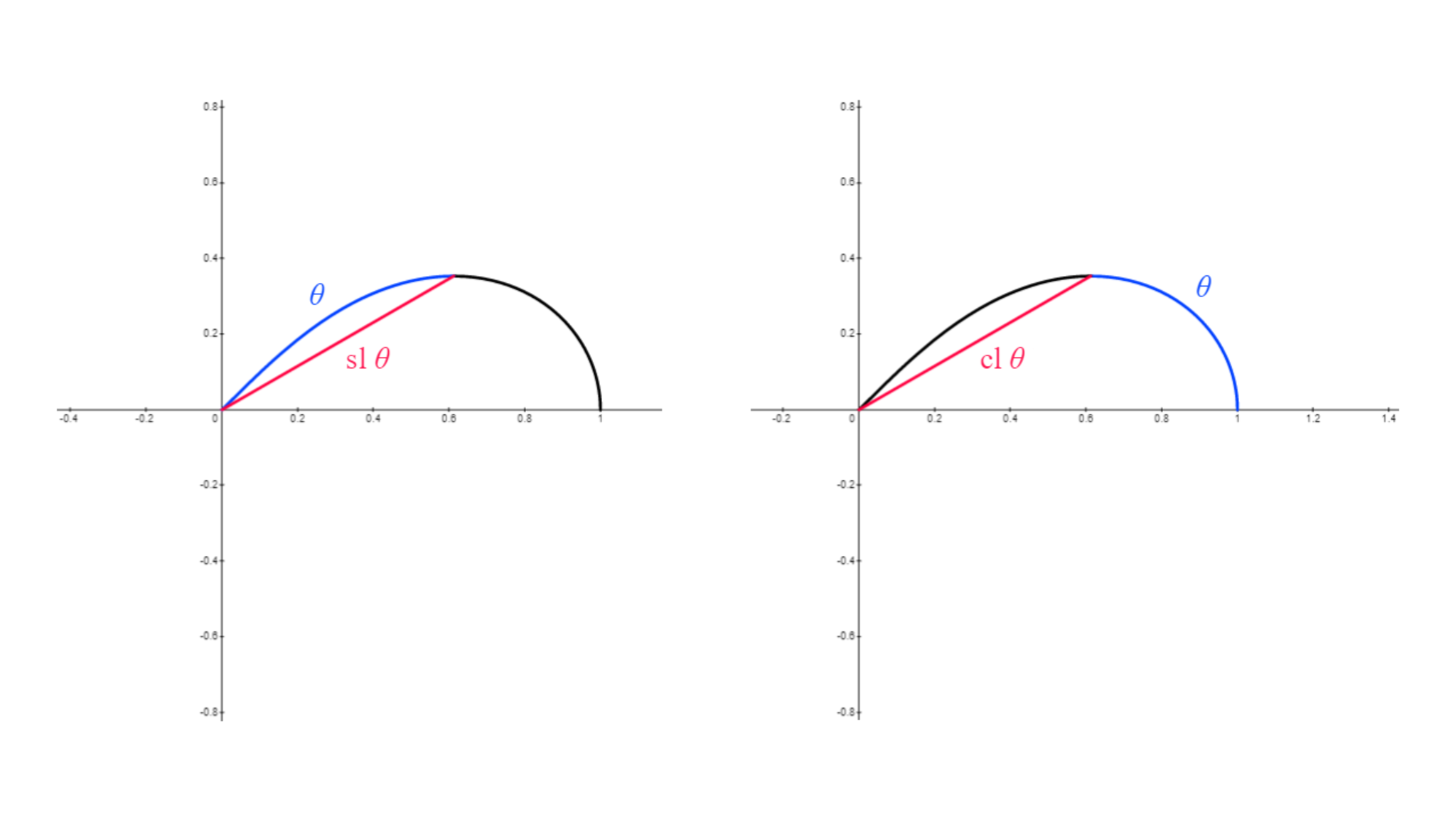 レムニスケートの定義については各自で調べよ
レムニスケートの定義については各自で調べよ
${\rm sl\,}\theta,{\rm cl\,}\theta$はそれぞれ「レムニスケートサイン」、「レムニスケートコサイン」と読み、これらを合わせてレムニスケート関数と呼称する。${\rm cl\,}$の${\rm c}$は${\rm cosine}$、${\rm l}$は${\rm lemniscate}$(もしくは${\rm leaf}$)を省略したもので、${\rm sl\,}$も同様である。……だったら三角関数は円関数と呼びそうなものだが、そこはまた歴史の話になってくるので省略しよう。
かくして定義された${\rm sl\,}\theta,{\rm cl\,}\theta$について、実は積分との相性が良い。詳細は省くが、$\displaystyle t={\rm sl\,}\theta \Longleftrightarrow \theta =\int_0^t \dfrac{dx}{\sqrt{1-x^4}},$$\displaystyle t={\rm cl\,}\theta \Longleftrightarrow \theta =\int_t^1 \dfrac{dx}{\sqrt{1-x^4}}$という関係がある。このため、レオンハルト・オイラーの時代から、${\rm sl\,}\theta,{\rm cl\,}\theta$についての研究が熱心に進められているそうだ。三角関数と同様の加法定理から無限級数に算術幾何平均まで、過去に私が記してきた面積・角度の性質とは比べ物にならないほどの先行研究が存在する。次節に掲載する性質も決してオリジナルではなく、膨大な先行研究を畏れ多くも拝借して書いたにすぎない。
${\rm sl\,}\theta,{\rm cl\,}\theta$がみたす、三平方の定理に類似した(?)性質
定義からして、レムニスケート関数は三角関数とよく似ている。だから、${\rm sl\,}\theta,{\rm cl\,}\theta$にも三平方の定理のような性質があると推測できる。この推測は正しく、 レムニスケート関数の英語版Wikipedia には「Pythagorean-like identity」として以下の性質が収載されている(項の順序を一部入れ替えた)。
${\rm sl^2\,} \theta+{\rm cl^2\,} \theta+{\rm sl^2\,} \theta \; {\rm cl^2\,} \theta=1$ (ただし、${\rm sl^2\,} \theta=({\rm sl\,} \theta)^2,$${\rm cl^2\,} \theta=({\rm cl\,} \theta)^2$を表す)
証明の大筋は参考文献の1つ、
20170327_レムニスケートにまつわる色々な計算
にQuestionとして掲載されている。証明さえも面倒になったらしい。
それよりも、定理2との類似性に注目していただきたい。確かに、レムニスケートの世界におけるPythagorean-likeな性質といえよう。先行研究すごい。
Is this the most "Pythagorean-like" theorem in lemniscate?
……けれども、はたしてこれは、「三平方」と呼べるだろうか。これは主観でしかないが、私は「三平方ではない」と答えたい。当然だ。左辺で4回も平方を計算しているのだから、定理3は「五平方の定理」と呼ばれて然るべきだろう。2乗が多すぎる。かのピタゴラスも黙っていない。
昨今の国際情勢では、ある案に反対するならば対案を出せ、と叫ばれる。「定理3を三平方と呼ぶな」と主張するならば、それに代わる定理を用意しなければならない。問題提起をなした者の責任として、民衆は改善案を期待する。だが、多くの数学者が定理3をPythagorean-likeとして認めている以上、既存の定理でこれ以上Pythagorean-likeなものは無いのだろう。レムニスケート幾何について全てを知っているわけではないが、状況証拠がそう推測させた。
そこで私は、独自研究に奔った。既存の定理に無いならば、見つけるまで。もしくは、作り出すまで。
時には古英語やラテン語で書かれた文献をも収集しつつ、より幾何学的・直感的な形で三平方を再現できないか、ひたすら試行錯誤を重ねた。座標計算の反故は千行を優に超え、1日のうち12時間ほどを研究に投じた日もあった(その日、残った12時間は睡眠だった)。
Twitterのダイレクトメッセージ機能を介して、初等幾何エンジョイ勢こと立見鶏氏も巻き込んだ。明らかに多忙をきわめているであろう氏へ話を振るのはかなり気が引けたのだが、座標計算とは対極をなす幾何学的な発想力は氏のほうが上手であるため、やはり必要であった。……正確には、氏に相談した時点では三平方の意識は薄く、次節に書いた定理より弱い性質(記事末尾にあります)しか持ち合わせていなかったのだが。
もっと三平方の定理に近づけたい!(ここから先行研究なし)
三平方の定理を模倣する以上は、どこかに直角を入れつつ、3回の平方計算で完結する定理にしたい。また、複雑な条件が絡んで汎用性や単純さを失うと、その時点で「三平方の定理に類似した」とは言えなくなってしまう。
研究中の私は、そのように思っていた。数学者というよりは芸術家のような視点で、定理を組み上げようとしていた。前回の記事【
レム・ツー・スリー・フォー ~レムニスケート上の点がつくる角度に関して~
】にも記した通り、『構図はビジュアルが命』なのだ。
結果、出来上がったものがこちらである。
点$O$を中心とするレムニスケート$L_1,L_2$が直交している。$L_1$上に点$P(\neq O)$をとり、「$P$で$L_1$と接し$O$を通る円」と$L_2$との交点を$X,Y$とする。「$P$を中心とし$X,Y$を通るレムニスケート」を$L_3$としたとき、$L_1,L_2,L_3$の周長をそれぞれ$a,b,c$とすると$a^2+b^2=c^2$が成立する。
さてここからが本題である
直交の条件はクリア。平方計算3回の条件もクリア。三平方に似せる条件もクリア。単純さの条件は……まあ、単純といえば単純か。
芸術作品としての定理は、このように仕上がった。改めて、定理1と見比べてもらいたい。3つの線分が織りなす関係について描かれた定理1と、3つのレムニスケートが織りなす関係について描かれた定理4。個人的には精緻に対応していると感じられるのだが、いかがだろうか。
${\rm sl\,}\theta,{\rm cl\,}\theta$ $<$ もしかして僕たちの出番ってもう無いの? ※そうです
「レムニスケート版『三平方の定理』」の証明
これまでのように根性を見せる座標計算で示すのもよいが、今回に限っては計算量が多すぎる。レムニスケートは4次曲線であり、単純に式を4乗する必要があることに加え、定理4には「回転したレムニスケート」までもが登場するからだ。24時間かけて計算しても証明が完了しなかった、とだけ述べておく。
代わりに、幾何学的なアプローチを用いる。突飛な発想を求められるものの、計算量が著しく軽減されるのが特長だ。今回は特に反転幾何の知識を多く動員するので、反転幾何を知らない読者は本節を読み飛ばし、別のWebサイト等で勉強してから戻ってくるのがよいだろう。
では、証明を書き始める。長くなるので、Mathlog標準書式である証明の括弧は用いない。
2つの補題を示す
中心を$O$とする円$\gamma_a$における反転で、$\gamma_a$の内部の点$A$は$B$に移る。$\gamma_a$上に点$C$をとり、中心を$C$とする円$\gamma_b$を描く。$\gamma_b$における反転で$A,B$がそれぞれ$A',B'$に移るものとすると、$A'$と$B'$は$\gamma_a$と$\gamma_b$の根軸に関して対称である。
 2箇所で反転する珍しい構図
2箇所で反転する珍しい構図
線分$AB$と$\gamma_a$の交点を$P$とし、$\triangle A'B'C$の外接円を$\gamma_c$とする。
このとき、$\gamma_a$は2点$A,B$からの距離の比が$AP:PB$であるような点の軌跡(アポロニウスの円)なので、$\angle ACP=\angle PCB$となる。直線$AB$を$\gamma_b$で反転すると$\gamma_c$に移ることから、$P$を$\gamma_b$で反転した点$P'$は$\gamma_c$における弧$A'B'$の中点といえる。
また簡単な角度計算より$\angle OCA'=\angle BA'C$が判るので$A'B' \parallel OC$であり、ここまでで強調した事実を統合すれば題意が示される。
なお、上記の証明より、$O$を$\gamma_b$で反転した点$O'$が$\gamma_a$と$\gamma_b$の根軸に関して$C$と対称であることも導かれる。つまり、線分$O'C$の垂直二等分線に関して$A'$と$B'$が対称だ、とも言い換えられる。この性質も使うので注意せよ。 (証明終)
直角な双曲線$\eta$の上に3点$A,B,C$をとり、これらを通る円$\gamma$を描く。$A$と$B$が$\eta$の中心に関して対称のとき、$A$から引いた$\eta$の接線と$C$から引いた$\gamma$の接線は平行である。
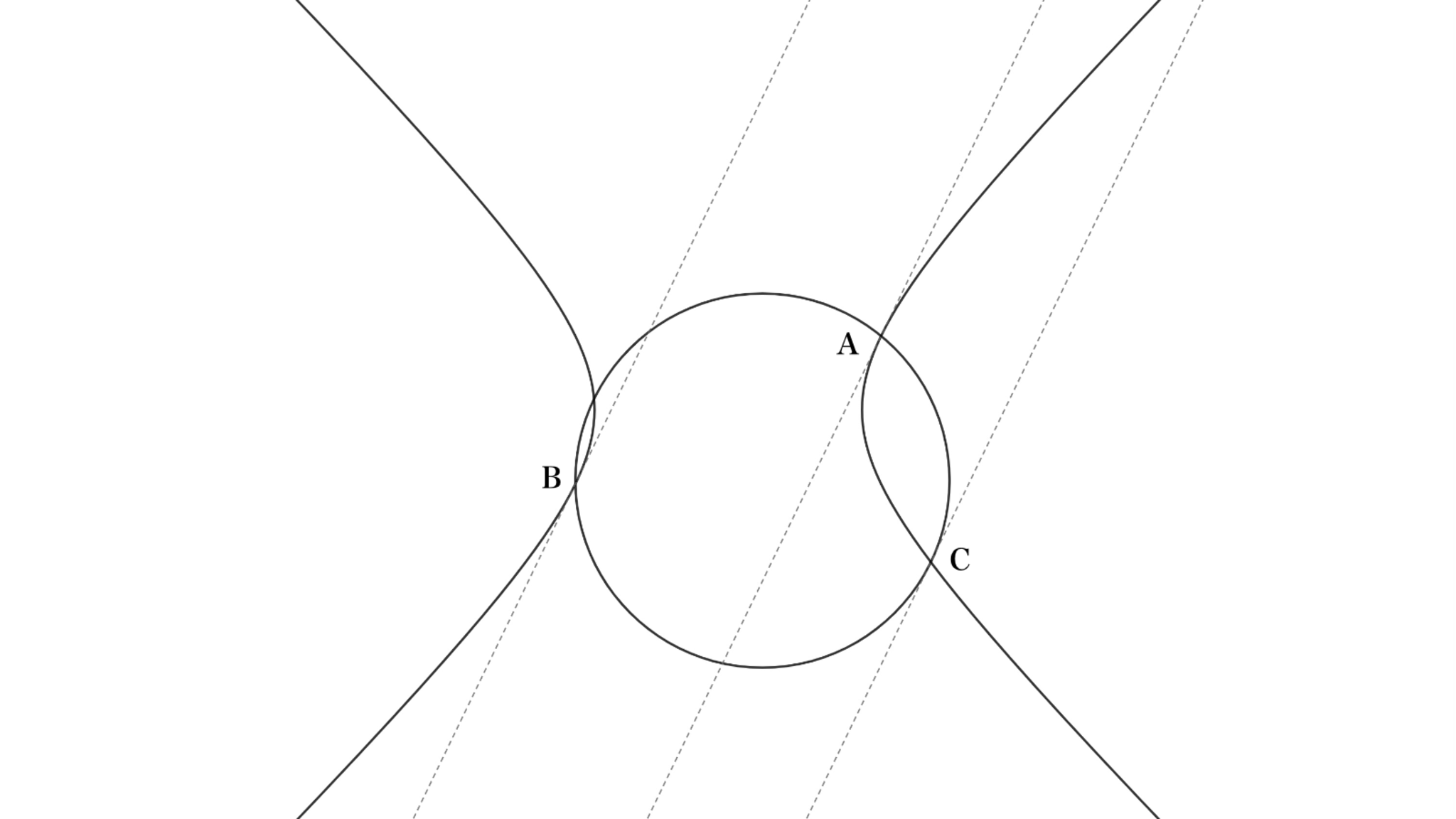 教科書に載せたいくらい汎用性が高い
教科書に載せたいくらい汎用性が高い
参考文献に挙げている「 A simple proof of Gibert's generalization of the Lester circle theorem 」の中に証明が載っている。そこまで疲れない座標計算。 (証明終)
余談だが、補題6を共同研究者の立見鶏氏に紹介したところ、「何となく(初等幾何で)行けそうな気がする」と仰ってから1時間弱で本当に初等幾何解法を完成させられた。氏が凄いのか初等幾何が凄いのか。
興味のある方は以下をクリックしていただきたい。
ここをクリックすると立見鶏氏による初等幾何証明が読めます
中心を$O$とする2次曲線$q$に、ある点$A$から接線を引く。接点を$X,Y$とし、線分$XY$の中点を$M$とする。
$({\rm lemma\;primo})$ 3点$A,O,M$は同一直線上に存在する。
$({\rm lemma\;secondo})$ $\angle XOY+\angle XAY={180}^{\circ}$が成立する。
以下の図の${\rm lemma}$と書いてある部分で、上記2つのどちらかを各々選択して使えばよい。 (証明終)
立見鶏氏提供、許可を得て掲載しています
3本の直角な双曲線を考察する
 元の定理どこいった?
元の定理どこいった?
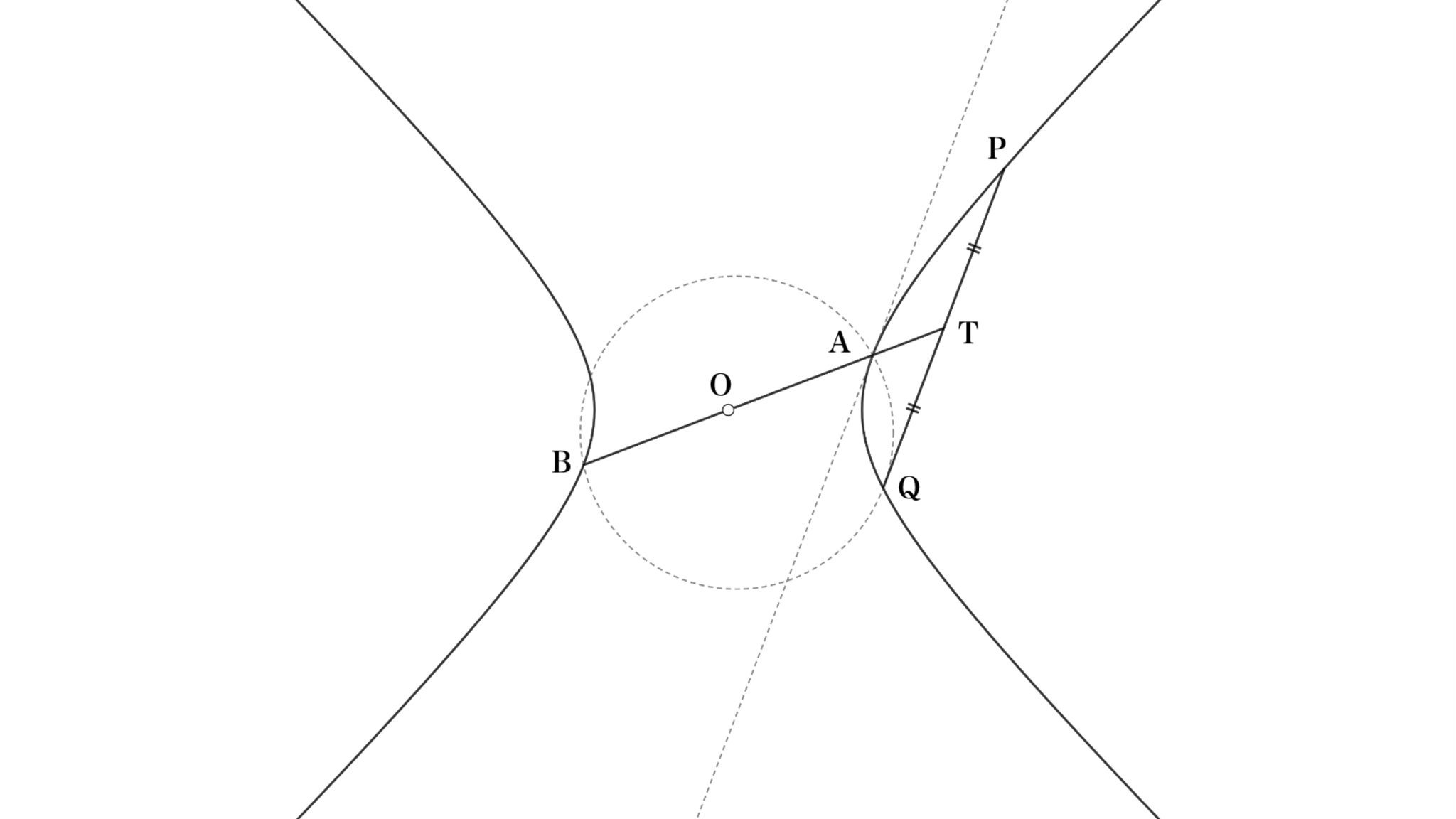
中心が$O$である直角な双曲線$\eta_1$の同じ枝の上に2点$P,Q$をとり、線分$PQ$の中点を$T$とする。直線$OT$と$\eta_1$の交点を$A,B$として、$\triangle ABQ$の外接円$\gamma_1$を描く。
2次曲線の一般的な性質として、$A$における$\eta_1$の接線は直線$PQ$と平行である。ここで補題6を用いると直線$PQ$が$\gamma_1$に接すると判るので、方べきの定理より$AT \times BT = QT^2$である。同様に$AT \times BT = PT^2$である。これを変形することで、$OT^2-OA^2=PT^2$を得る。
 OA^2+PT^2=OT^2←これ三平方では?
OA^2+PT^2=OT^2←これ三平方では?
$\dfrac{OT}{OA}=u$とおく。$O$を中心として、$\eta_1$を$u$倍に拡大した双曲線$\eta_2$を考える。線分$PQ$は明らかに$\eta_2$と$T$で接しており、$\dfrac{PT}{OT}=\dfrac{\sqrt{OT^2-OA^2}}{OT}$$=\sqrt{1-\left(\dfrac{OA}{OT}\right)^2}$$=\dfrac{\sqrt{u^2-1}}{u}$が成り立つ。
このことから、次の事実が導かれる。
$|u|>1$とする。原点$O$の$xy$直交座標平面上に描かれた2本の直角な双曲線
$$ \eta_1: x^2-y^2=1\,\quad\eta_2: x^2-y^2=u^2$$
において、$\eta_2$上の点$T$から引いた接線が$\eta_1$と交わる点を$P,Q$とすると、$\dfrac{PT}{OT}=\dfrac{\sqrt{u^2-1}}{u}$が成り立つ。
今、ここに3つ目の双曲線$\eta_3: x^2-y^2=-\dfrac{u^2}{u^2-1}$を描き加えてみる。
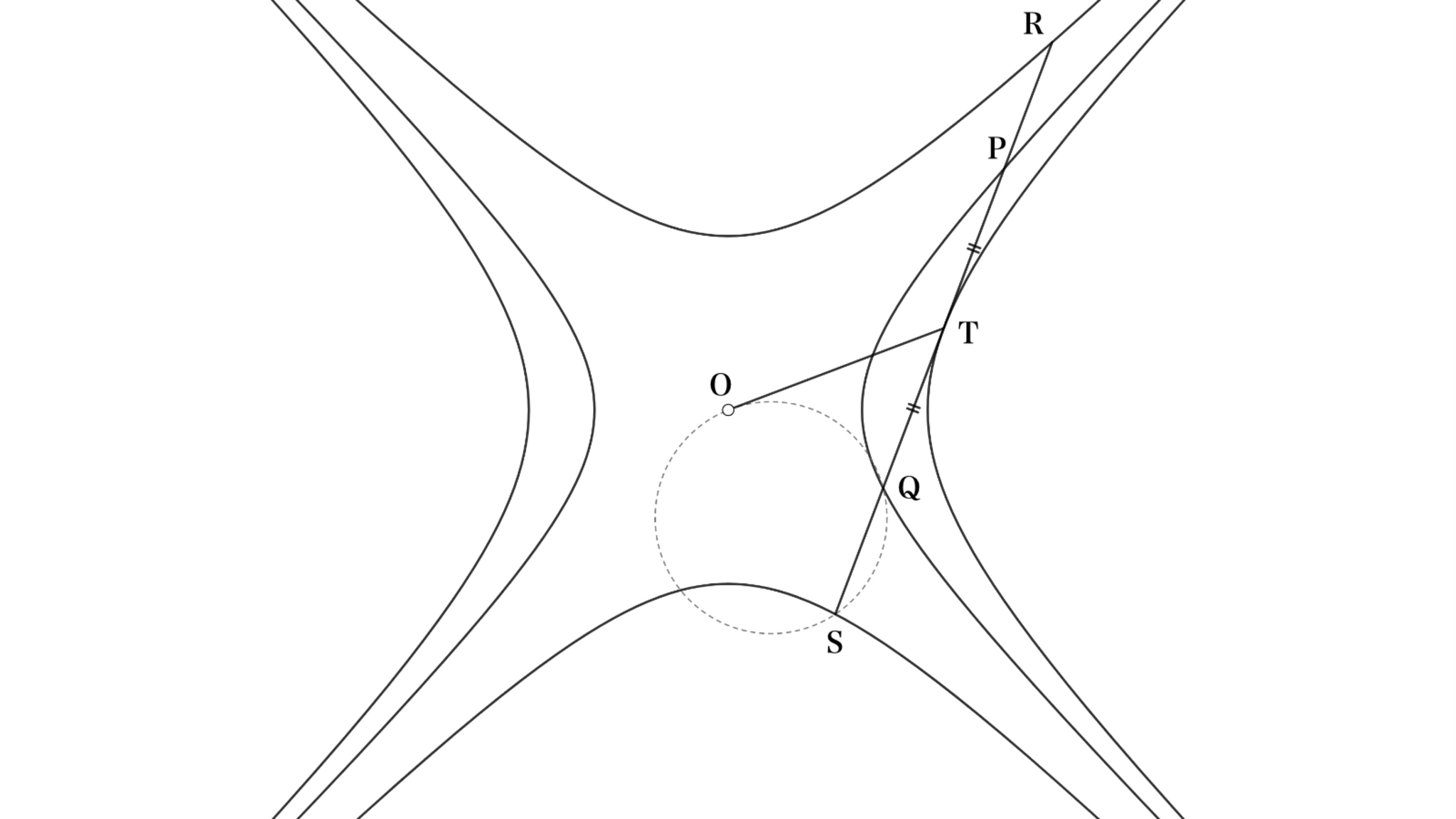 点線で描いた円に深い意味は無い(消し忘れ)
点線で描いた円に深い意味は無い(消し忘れ)
直線$PQ$と$\eta_3$の交点を$R,S$として、補題7を導いた際の考え方を参考にすると(ここの行間がかなり広い、「$\eta_3$は$\eta_1$を$\dfrac{i}{\sqrt{u^2-1}}$倍に拡大した双曲線である」というイメージを持てるかどうか)、$\dfrac{RT}{OT}=\sqrt{1-\dfrac{-\dfrac{u^2}{u^2-1}}{u^2}}$より$\dfrac{RT}{OT}=\dfrac{u}{\sqrt{u^2-1}}$となる。
ゆえに$\dfrac{PT}{OT} \times \dfrac{RT}{OT} = 1$、すなわち$PT \times RT = OT^2$が従う。つまり、中心が$T$で半径が$OT$の円$\gamma_2$を考えれば、$P$と$R$は$\gamma_2$における反転で移り合う($Q$と$S$についても同様)。
反転して仕上げ
さて、$O$を中心とし$\eta_1$に接する円$\gamma_3$を描いて、$\gamma_3$でこれまでの図を反転してみよう。「直角な双曲線を同心の円で反転すると同心のレムニスケートになる」という有名な性質が知られており、ここから$\eta_1,\eta_2,\eta_3$の反転先をそれぞれレムニスケート$\lambda_a,\lambda_b,\lambda_c$とおける(添字が対応していないのは製図時のミスです、申し訳ございません)。
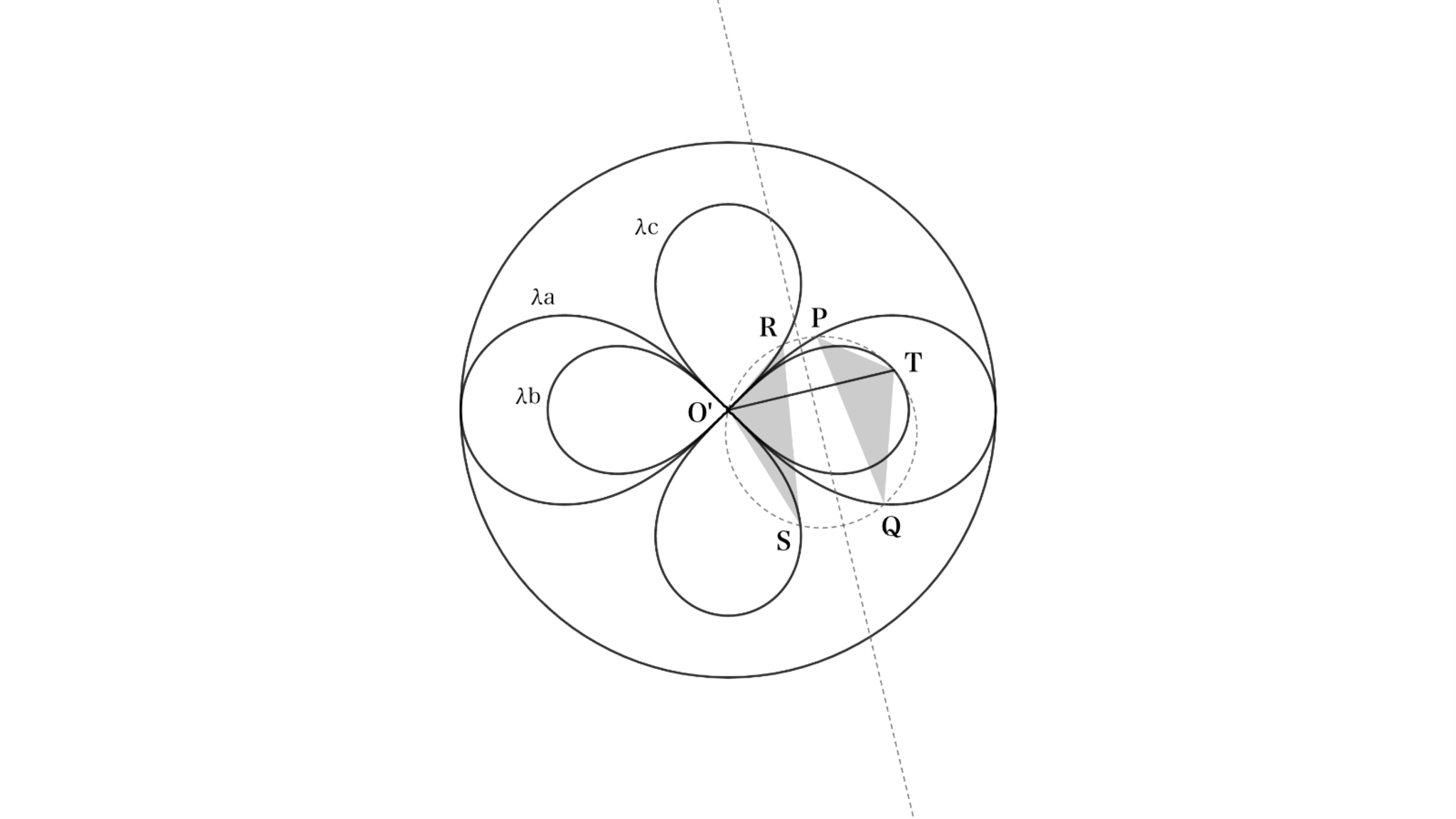 唐突に現れた直交レムニスケートさん
唐突に現れた直交レムニスケートさん
上図が反転したものである(無限遠点の反転先(要するに$\gamma_3$の中心)を$O'$とした)。線分$O'T$の垂直二等分線を$l$とすると、補題5より、$P$と$R$、$O'$と$T$、$Q$と$S$はそれぞれ$l$について対称であるから、$\triangle PQT \equiv \triangle RSO'$が導かれる。長らく出番のなかった補題5はここで使う。
反転前の図で、5点$P,Q,R,S,T$を通る直線は$\eta_2$と$T$で接していた。したがって反転後の図で、6点$O',P,Q,R,S,T$を通る円は$\lambda_b$と$T$で接している。ということは、$\lambda_a$を$l$で対称移動させたレムニスケート${\lambda_a}'$こそが「接点$T$を中心とし、2つの交点$R,S$を通るレムニスケート」なのだ(逆に、このようなレムニスケートは一意に定まる)。ようやく定理4の面影が見えてきた。
あとは${\lambda_a}',\lambda_b,\lambda_c$について三平方の関係が成り立つことを示せばよい($u$の値は任意であるから、定理4において考えるべき図を網羅できている)。反転の定義から、3つのレムニスケート$\lambda_a,\lambda_b,\lambda_c$の相似比は$\lambda_a:\lambda_b:\lambda_c=1:\dfrac{1}{u}:\dfrac{\sqrt{u^2-1}}{u}$である。周長の比は相似比に一致し、かつ${\lambda_a}' \equiv \lambda_a$、$\left(\dfrac{1}{u}\right)^2+\left(\dfrac{\sqrt{u^2-1}}{u}\right)^2=1^2$であるから、定理は示された。 (証明終)
あとがき
証明が済んだので堂々の再掲
ここまで通しで読んでくれた読者も、冒頭の注意書きに従って本節から読み始めた読者も、ひとまずお疲れ様と言いたい。スクロールだけでも1日の摂取カロリーの50%ほどを消費されたのではなかろうか。実際、ここまで長いMathlog記事は数えられるほどしか知らない。どうしてこんなものを書こうとしたのか、永遠の謎である。
レムニスケート版『三平方の定理』の話題に戻ろう。本定理において特筆すべきは、「$L_3$の周長は$L_1,L_2$の周長のみに依存し、円の位置に依らない」という点である。円が$L_1$のどこに接していても、$L_3$の大きさに影響を与えない。以下の図において、点線で描かれたレムニスケートは全て同じ大きさとなるのだ。
カラフルは正義
これこそが、私の考えるレムニスケート版『三平方の定理』である。「いやいや、こちらのほうが三平方の名を冠するに相応しい」という構図を、もしくは「君の定理は〇〇という論文に掲載されている」という先行研究をご存知の読者がいらっしゃれば、本記事のコメントか Twitter でご教示ねがいたい。
最後になるが、本定理の研究にあたって様々な初等幾何学的考察を提供してくださった立見鶏氏に、改めて感謝を送る。氏の存在なしには、定理を見つけることこそ出来たとしても、何日もかけて煩雑きわまりない座標計算を熟すしか手立てが無かったのだから。あと補題6の証明図も。ありがとうございます。
あと少しだけ……
最後の最後に、本定理を応用した自作問題を紹介し、記事を締めくくることにする。しばらく更新が滞ると思われるものの、次の記事も変わらず読んでいただければ有難い。
?の面積を求めなさい。
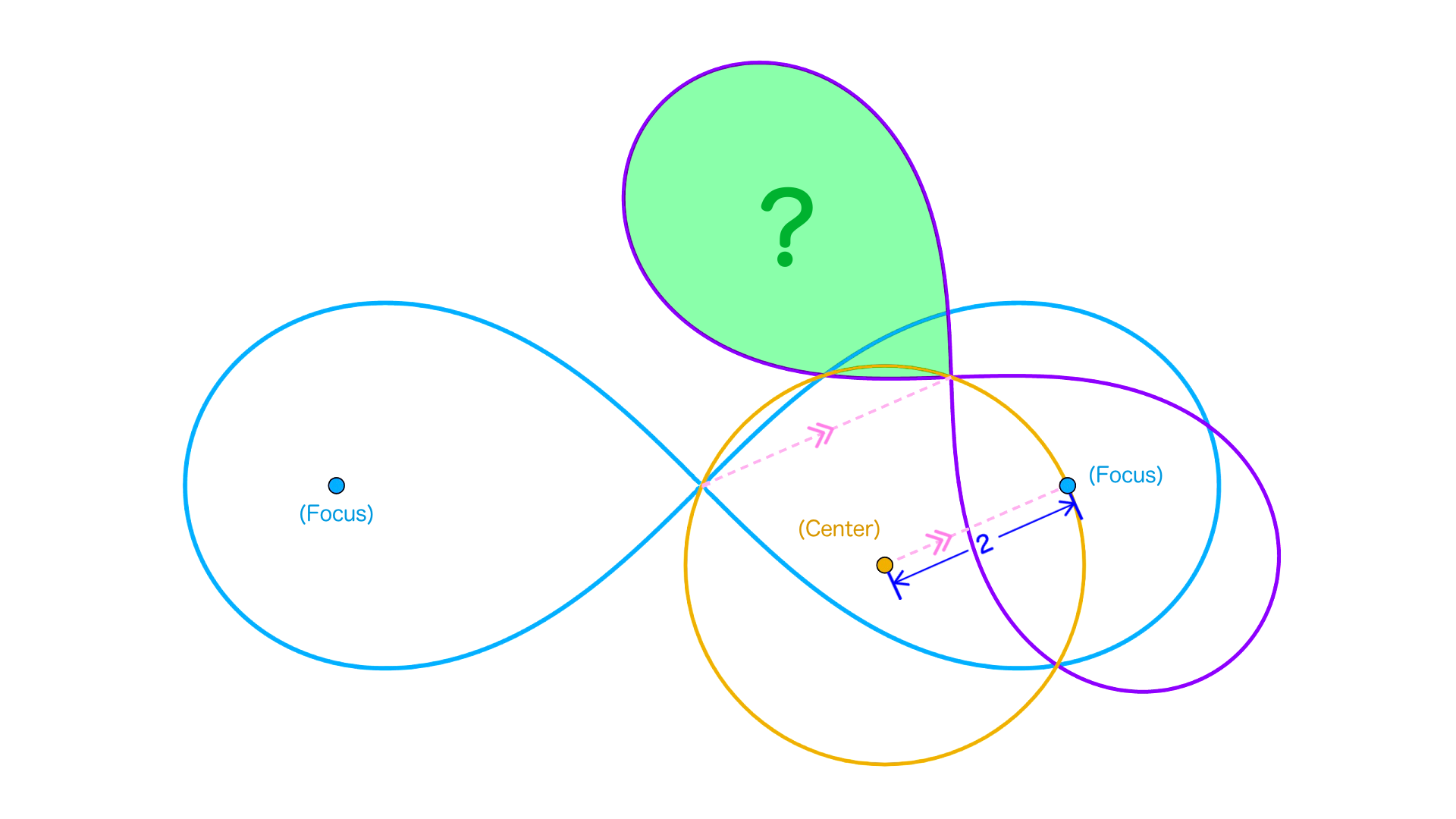 実際にはこの問題から逆に三平方を見出したのですがね
実際にはこの問題から逆に三平方を見出したのですがね
ヒント
水色のレムニスケートを、中心はそのままに、円に接するまで縮小してみましょう。
……何か見落としている気がする。通常の三平方の定理にあって、レムニスケート版『三平方の定理』にないもの。平方計算の回数はどちらも3回だった。どちらも3つのオブジェクトのうち2つが直交する構図だった。性質自体の単純さはどちらにもあった。卓越した汎用性……あっ。
ま、まあ、本記事を読んでくださった方々が何かしらの形で定理を駆使してくれれば、汎用性があると言い張ることもできよう。ということで誰か使ってくださいお願いします。
