平方因子を持たない自然数に対する素微分の上下からの評価
今回の記事の正確性においては不安しかないです
前提知識
$p_i$を0から数えてi番目の素数とする。また$q_i$は有理数とする。
$n=\overset{\infty}{\underset{i=0}{\prod}}{p_i}^{q_i}$と書けるとき、素微分$D$を以下のように定義する。
\begin{align}
D(n) := n\sum_{i=0}^{\infty}\frac{q_i}{p_i}
\end{align}
例えば$D(840)$なら、$840=2^3\cdot3^1\cdot5^1\cdot7^1$なので、
\begin{eqnarray}
p_1&=&2&,&p_2=&\:3,&p_3&=&5&,&p_4&=&7&,&p_5&=&11&,&p_6&=&&13&&\cdots&\\
q_1&=&3&,&q_2=&\:1,&q_3&=&1&,&q_4&=&1&,&q_5&=&0&,&q_6&=&&0&&\cdots&
\end{eqnarray}
となるので
\begin{eqnarray}
D(840) &=& 840\sum_{i=0}^{\infty}\frac{q_i}{p_i}
\\&=&840\qty(\frac{3}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{0}{11}+\frac{0}{13}+\frac{0}{17}+\cdots)
\\&=&840\cdot\frac{315+70+42+30}{210}
\\&=&840\cdot\frac{457}{210}
\\&=&1828
\end{eqnarray}
となります。
必要な知識はこれだけです。
もっと知りたい人:
素微分についての記事(数学を愛する会Wiki)
平方因子を持たない自然数とは
自然数$n$が平方因子をもたないというのは$n$を素因数分解したときに$p^2$の形の素数が出てこないということです
無平方とも言い、wikipediaには
1 より大きい完全平方で割り切れないような整数
とありました。
まぁ要は 1より大きい平方数 の倍数でない数です。
このような数$n$の素因数分解は
\begin{eqnarray}
n = p_1p_2p_3\cdots
\end{eqnarray}
という感じで$2$乗が出てこないです(定義より当たり前)
なぜ平方因子をもたない自然数だけ素微分を考えるのか
私の前回の記事
素微分友愛数は互いに素である簡単？な証明
や、
その前回の記事を書く元となった記事
素微分友愛数となる相異なる自然数同士は互いに素
にあるように、
私は素微分友愛数について考えていて、
素微分友愛数は次のような性質を持ちました
素微分友愛数である自然数$n,m$については、以下のいずれかが成り立つ。
- $n=m$ (素微分完全数)
- $n,m$が互いに素
そう、素微分友愛数となる相異なる自然数同士は互いに素になるのです。
さらに、次の公式が成り立ちます。
$a,b$は自然数とする
\begin{eqnarray}
D(ab) =D(a)b+aD(b)
\end{eqnarray}
$p$を素数とし、$n$を自然数とする
\begin{eqnarray}
D(p^n) = np^{n-1}
\end{eqnarray}
なので、例えば$n$を平方因子を持つ自然数だとします。
その$n$の平方因子から一つ素数をとってきて$p$とすると、
\begin{eqnarray}
n = p^2k
\end{eqnarray}
となるような自然数$k$が存在します。
この$n$の素微分はこうなります。(公式を使っていく)
\begin{eqnarray}
D(n) &=& D(p^2k)
\\&=& D(p^2)k + p^2D(k)
\\&=& 2pk+p^2D(k)
\\&=& p\big(2k+pD(k)\big)
\end{eqnarray}
よって$D(n)$は$p$で割り切れます。
つまり、$n$と$D(n)$は互いに素ではないということです！
こうなってしまうと$n$はもう素微分友愛数にはなりえません
(素微分完全数にはなる可能性がある)
こういう経緯から平方因子を持たない自然数の素微分に興味を持ったのです。
そもそも
そもそも、自然数を素微分した表とかグラフってあんまり見てないですよね
数値計算bot
が具体的な値の計算をしています。
1~100000000(1 Billion)まで求めていますね。
しかしこれはでかすぎます。 22GBあります。(中身は100個のテキストファイルで1つ228MB)
幸い1 ~ 100000の2.28MBのテキストファイルバージョンがありました
これならぎり開けます。
CSV形式になっていますね
グラフにしたいので1~1000ぐらいをコピーしてDesmosに張り付けました
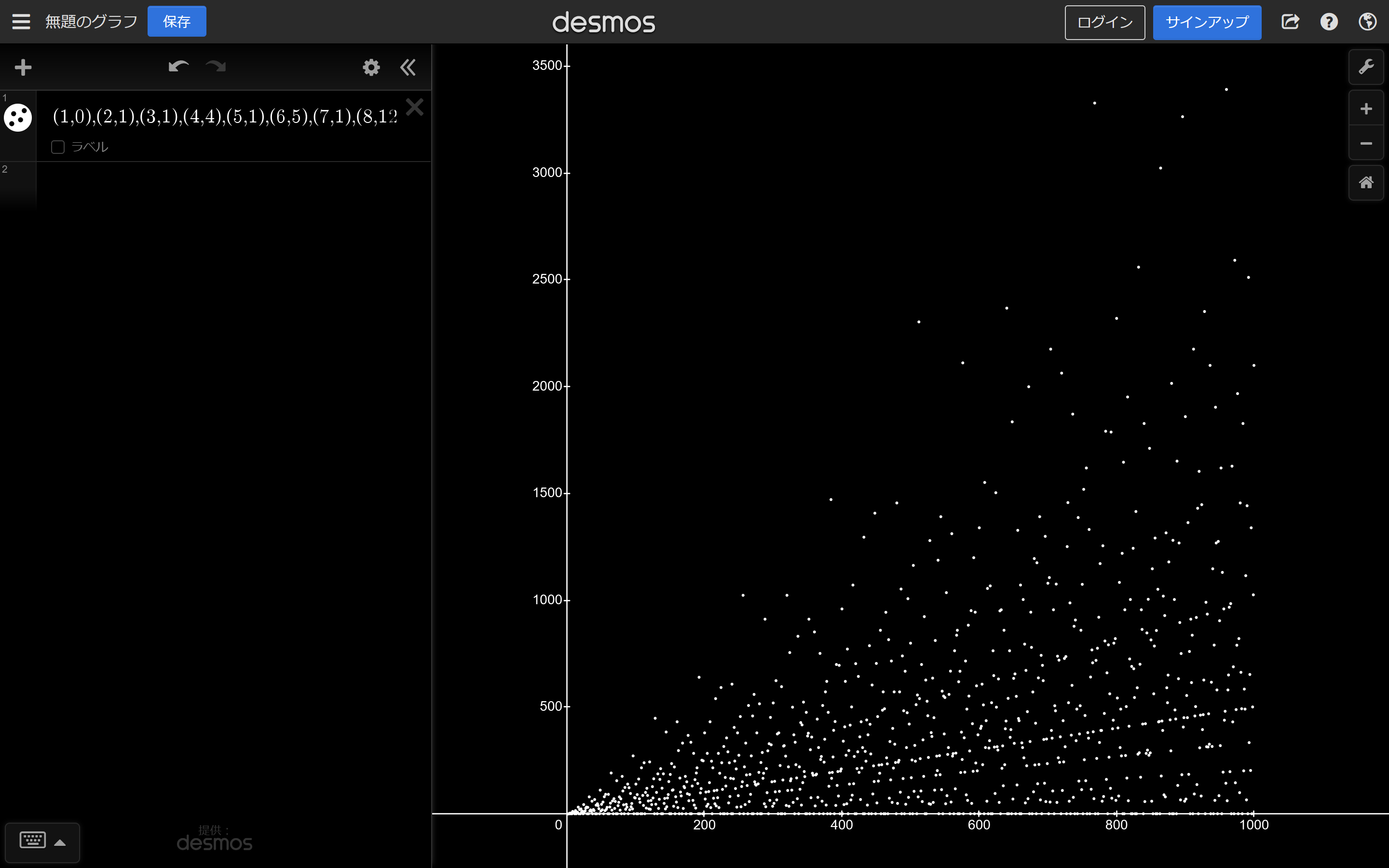1~1000までの点
ここで見れます Desmos
うわー
そして平方因子を持たない自然数だけプロットするとこうなります
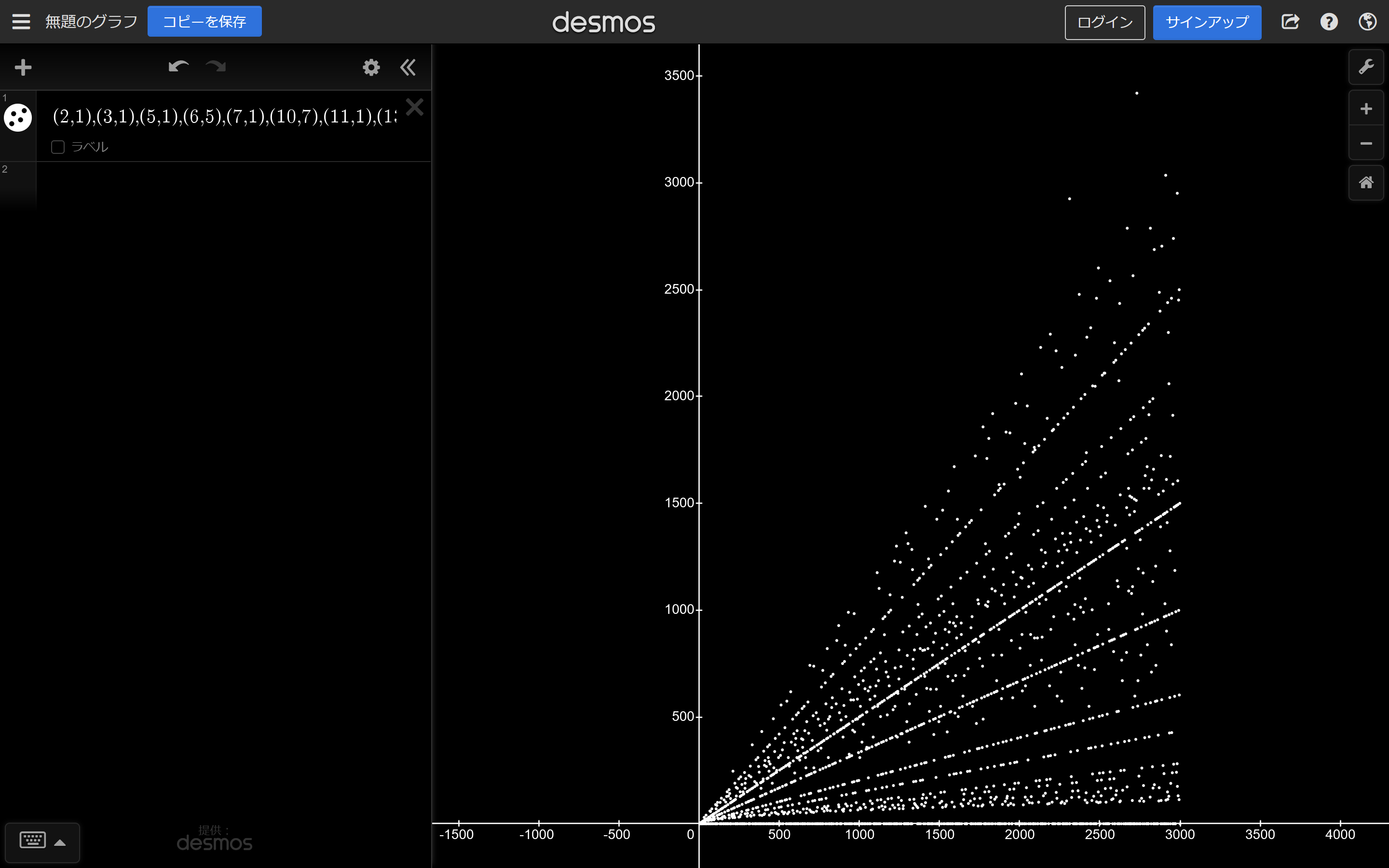
1~3000までプロットしてみました
Desmos
評価していく
まずここからは$n$は平方因子を持たない自然数ということにします。
そして$p_i$は$n$の素因数の小さいほうから$i$番目ということにします。
なので素因数分解はこうなります。
\begin{eqnarray}
n = \prod_{i} p_i
\end{eqnarray}
つまりは
\begin{eqnarray}
n = p_1p_2p_3p_4\cdots
\end{eqnarray}
ということになります。
下限
下からはどう抑えられそうでしょうか?
まず$n$が素数$p$の時、
\begin{eqnarray}
D(n) &=& D(p)
\\&=& 1
\end{eqnarray}
なので下限は$1$です。
う～ん
もうちょっといい下限はないでしょうか？
例えば$n$が合成数の時とかね？
\begin{eqnarray}
D(n) &=& n\sum_{i}\frac{1}{p_i}
\\&=& n\qty(\frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}+\cdots)
\end{eqnarray}
$D(n)$を展開するとこんな感じで書けます。
なので、素因数が多ければ多いほど$D(n)$も大きくなります。
逆に言うと$D(n)$を小さくするには素因数を減らせばいいのです。
なので$n=p_1p_2$となったときが一番小さいでしょう(多分)
\begin{eqnarray}
D(n) &=& D(p_1p_2)
\\&=& p_1D(p_2) + D(p_1)p_2
\\&=& p_1 + p_2
\end{eqnarray}
ここで相加相乗平均の式より、
\begin{eqnarray}
p_1 + p_2 &\ge& 2\sqrt{p_1p_2}
\\&=& 2\sqrt{n}
\end{eqnarray}
です。
よって、素数でない$n$に対しては
\begin{eqnarray}
D(n) \ge 2\sqrt{n}
\end{eqnarray}
が成り立ちます。
が、$n$は平方因子を持たない自然数なので平方数にはなることはありません。
よって
\begin{eqnarray}
D(n) > 2\sqrt{n}
\end{eqnarray}
が成り立ちます。
上限
上限の方はちょっとむずいですよ
\begin{eqnarray}
D(n) &=& n\sum_i \frac{1}{p_i}
\\&=& n\qty(\frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}+\cdots)
\end{eqnarray}
なので、同程度の大きさの$n$同士では$p_i$が多いほうが$D(n)$も大きくなります
実際、図3の右上の方に飛び出している二つの点は$2310$と$2730$で、素因数分解すると$2310=2\cdot3\cdot5\cdot7\cdot11$と$2730=2\cdot3\cdot5\cdot7\cdot13$と
小さいほうから素数を掛け算していった数になっています。
これは平方因子を持たない自然数のなかでは素因数を多く持ちつつ大きさも抑えられているので、上の方に飛び出しているわけです。
ということで、小さいほうから素数をかけていった数に注目してみましょう
そういう数は素数階乗を使うときれいに書けます
素数階乗の素微分
素数階乗のWiki には、こう書いてあります
素数階乗（そすうかいじょう、英: Primorial）とは、$2$以上の自然数に対してそれ以下の素数全ての総乗のことである。自然数$n$の素数階乗は、記号では$n\#$で表す。
なるほど
例としてはこんな感じです
\begin{eqnarray}
2\# &=& 2 \\
3\# &=& 2\cdot3 = 6 \\
4\# &=& 2\cdot3 = 6 \\
5\# &=& 2\cdot3\cdot5 = 30 \\
6\# &=& 2\cdot3\cdot5 = 30 \\
7\# &=& 2\cdot3\cdot5\cdot7 = 210 \\
\end{eqnarray}
この素数階乗には次のような評価が知られています 英語版Wikiの素数階乗
自然数$n\ge2$について
\begin{eqnarray}
n \le 2.763^n
\end{eqnarray}
また、$n\ge563$については
\begin{eqnarray}
n \ge 2.22^n
\end{eqnarray}
ちなみに
\begin{eqnarray}
\lim_{n\to\infty} \sqrt[n]{n\#} = e
\end{eqnarray}
この評価は使えそうですね
さて、この素数階乗を素微分するとどうなるでしょうか
ここでは$n=m\#$としましょう
\begin{eqnarray}
D(n) &=& D(m\#)
\\&=& m\#\sum_{i}\frac{1}{p_i}
\\&=& m\#\qty(\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots)
\end{eqnarray}
そういえば、$m\#$はいくつまでの素数をかけているんでしょうか？
ここで使えるのが、素数計数関数です。
素数計数関数
素数計数関数というのはWikipediaにはこう書いてあります。 素数計数関数
素数計数関数（英: Prime-counting function）とは、正の実数にそれ以下の素数の個数を対応させる関数のことであり、$π(x)$ で表す
素数計数関数のWikipediaの記事の内容に加えて英語版のWikipediaの記事も見るのをお勧めします。 英語版Wikipedia 素数計数関数
つまりは$x$以下の素数の数を$\pi(x)$で表そうということです
例としてはこうです
\begin{eqnarray}
\pi(2) &=& 1 \\
\pi(3) &=& 2 \\
\pi(4) &=& 2 \\
\pi(5) &=& 3 \\
\pi(6) &=& 3 \\
\pi(7) &=& 4
\end{eqnarray}
この素数計数関数に対しては次の評価が知られています。
\begin{eqnarray} \frac{x}{\log x} < \pi(x) < 30\frac{\log 113}{113} \frac{x}{\log x} \end{eqnarray}
この素数計数関数を使うと$m\#$はこう書けます
\begin{eqnarray}
m\# &=& \prod_{i=1}^{\pi(m)} p_i
\end{eqnarray}
これを使うと、$D(n)$はこのようになります
\begin{eqnarray}
D(n) &=& D(m\#)
\\&=& m\# \sum_{i=1}^{\pi(m)} \frac{1}{p_i}
\\&=& m\# \bigg(\;\underbrace{\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots}_{\pi(m)\text{個}}\;\bigg)
\end{eqnarray}
素数の逆数和
さて、上記の式を評価するのに必要なのはやはり
\begin{eqnarray}
\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots
\end{eqnarray}
の評価ですね。
これの無限和はよく素数の逆数和として知られています。
残念ながら日本語のWikipediaの記事は無いですが、英語版ならあります。
Divergence of the sum of the reciprocals of the primes
ここでは素数の逆数和(sum of the reciprocals of the primes)が発散(Divergence)することについて書かれています。
素数の逆数和はにはこのような評価が知られています。
\begin{eqnarray} \sum_{\substack{p\text{ prime} \\ p \le n}} \frac{1}{p} \ge \log\log(n+1) -\log\frac{\pi^2}{6} \end{eqnarray}
なるほど、$\log\log(n)$程度の増加をするんですね
...
ちょっと待ってください。上からの評価はどうしたんですか？
探したんですが、見つけたのは
\begin{eqnarray}
\sum_{\substack{p\text{ prime} \\ p \le n}} \frac{1}{p} < 2e^2\qty(\frac{1}{\log\log3}+1)\log\log n
\end{eqnarray}
というもので、だいたい$172\log\log n$ぐらいの評価でした。
この不等式を示しているサイト
素数の逆数和を上から評価する
んん～
もうちょっと頑張りたいですね。
サイトの証明に従ってもうちょっときつい評価を得られないでしょうか？
もとのサイトではこのような不等式がありました。$(k\ge1)$です。
\begin{eqnarray}
\qty(\sum_{p\le n}\frac{1}{p})^k &=& \sum_{p_1,p_2,\cdots p_k< n}
\frac{1}{p_1p_2\cdots p_k} <
\sum_{m\le n^k} \frac{k!}{m}
\end{eqnarray}
？？？？？
つまり
\begin{eqnarray}
\qty(\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots)^k
\end{eqnarray}
は$k$個の$n$未満の素数$p_1,p_2,p_3,\cdots ,p_k$の積$p_1p_2p_3\cdots p_k$が取りうるすべての数の逆数和
\begin{eqnarray}
\sum_{p_1,p_2,\cdots p_k< n}\frac{1}{p_1p_2\cdots p_k}
\end{eqnarray}
と等しいと。
そしてその積$m=p_1p_2p_3\cdots p_k$の値というのは$n^k$以下であって、($p\le n$だからね)
多くても$k!$回しか出てこないと
だから
\begin{eqnarray}
\sum_{m\le n^k}\frac{k!}{m}
\end{eqnarray}
が右側にあると
なるほど？
難しいこと言いますね
でも、よく考えたら
\begin{eqnarray}
\qty(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots)^k
\end{eqnarray}
という風に$1$を足してもいいですよね？
\begin{eqnarray}
\qty(1+\sum_{p\le n}\frac{1}{p})^k < \sum_{m\le n^k}\frac{k!}{m}
\end{eqnarray}
これでも大丈夫なはずです。
そして右辺を評価していきます
\begin{eqnarray}
\sum_{m\le n^k}\frac{k!}{m} &=& k!\sum_{m\le n^k}\frac{1}{m}
\\&<& \sqrt{2\pi k}\qty(\frac{k}{e})^{k}e^{\frac{1}{12k}} \cdot \qty(\log \qty(n^k)+1)
\end{eqnarray}
なので
\begin{eqnarray}
1+\sum_{p\le n}\frac{1}{p} &<& \qty(\sum_{m\le n^k}\frac{k!}{m})^{\frac{1}{k}}
\\&<& \qty(\sqrt{2\pi k}\qty(\frac{k}{e})^{k}e^{\frac{1}{12k}} \cdot \qty(\log \qty(n^k)+1))^{\frac{1}{k}}
\\&=& k\cdot\qty(2\pi k)^{\frac{1}{2k}}e^{\frac{1}{12k^2}-1} \cdot
\qty(k\log n+1)^{\frac{1}{k}}
\end{eqnarray}
となります。
これにはスターリングの近似公式と調和級数の評価を用いました
自然数$n$に対して
\begin{eqnarray}
n! \le \sqrt{2\pi n}\qty(\frac{n}{e})^ne^{\frac{1}{12n}}
\end{eqnarray}
Wikipedia
自然数$n$に対して
\begin{eqnarray}
\sum_{i=1}^n \frac{1}{i} < \log(n)+1
\end{eqnarray}
高校数学の美しい物語
ここからは$k=\lfloor1+\log\log n\rfloor$とします。($\lfloor x \rfloor$は床関数)
ちょっと粗いかもしれませんが
\begin{eqnarray}
0<\frac{1}{k} \le 1
\end{eqnarray}\begin{eqnarray}
\frac{1}{12k^2}-1 \le -\frac{11}{12}
\end{eqnarray}\begin{eqnarray}
(2\pi k)^\frac{1}{k} \le 2\pi \quad\quad (k\text{が自然数なので})
\end{eqnarray}
さらに、
\begin{eqnarray}
&&(k\log n+1)^{\frac{1}{k}}
\\&<& (ke^{k}+1)^{\frac{1}{k}}
\\&<& ((k+1)e^k)^{\frac{1}{k}}
\\&=& e(k+1)^{\frac{1}{k}}
\end{eqnarray}
これを$y$として$k$で対数微分すると
\begin{eqnarray}
y &=& e(k+1)^{\frac{1}{k}} \\
\log y &=& 1+\frac{1}{k}\log(k+1) \\
\frac{y'}{y} &=& -\frac{1}{k^2}\qty(\frac{k}{k+1}-\log(k+1)) \\
y' &=& -\frac{e(k+1)^{\frac{1}{k}}}{k^2}\qty(\frac{k}{k+1}-\log(k+1)) < 0
\end{eqnarray}
よって$y$は単調減少なので、$k>1$では$k=1$の時以下になるはずです。
$y\le e(1+1)^{\frac{1}{1}} = 2e$
より、
\begin{eqnarray}
(ke^k+1)^{\frac{1}{k}} < 2e
\end{eqnarray}
とわかります。
($n\ge16$で$k\ge2$なので、そっちを使ってもいいですがね...)
(ていうかグラフ見たらだいたい$4$未満だなってわかるけどね...)
\begin{eqnarray} 0<\frac{1}{k}\le1 \quad,\quad \frac{1}{12k^2}-1 \le-\frac{11}{12} \quad,\quad (2\pi k)^\frac{1}{k} \le 2\pi \quad,\quad (ke^k+1)^{\frac{1}{k}} < 2e \end{eqnarray}
ということを使うと
\begin{eqnarray}
&&k\cdot\qty(2\pi k)^{\frac{1}{2k}}e^{\frac{1}{12k^2}-1} \cdot
\qty(k\log n+1)^{\frac{1}{k}}
\\&<& k\cdot \sqrt{2\pi}e^{-\frac{11}{12}} \cdot 2e
\\&=& 2\sqrt{2\pi}e^\frac{1}{12}k
\end{eqnarray}
綺麗になりました。
結論として
\begin{eqnarray}
1+\sum_{p\le n}\frac{1}{p} &<& 2\sqrt{2\pi}e^{\frac{1}{12}}(1+\log\log n) \\
\sum_{p\le n}\frac{1}{p} &<& 2\sqrt{2\pi}e^{\frac{1}{12}}(1+\log\log n)-1
\end{eqnarray}
となります
だいたい
\begin{eqnarray}
2\sqrt{2\pi}e^{\frac{1}{12}} \approx 5.4489288446816909936
\end{eqnarray}
です
特に
気になるのですが$16(>e^e)$以上の$n$ではもうちょっとタイトな評価が得られそうです。
\begin{eqnarray}
k = \lfloor1+\log\log n\rfloor \ge \lfloor1+\log\log e^e\rfloor = 2
\end{eqnarray}
なのでこうなります。
\begin{eqnarray} 0<\frac{1}{k}\le\frac{1}{2} \quad,\quad \frac{1}{12k^2}-1 \le-\frac{47}{48} \quad,\quad (2\pi k)^\frac{1}{k} \le 2\sqrt{\pi} \quad,\quad (ke^k+1)^{\frac{1}{k}} \le \sqrt{2e^2+1} \end{eqnarray}
よって
\begin{eqnarray}
&&k\cdot\qty(2\pi k)^{\frac{1}{2k}}e^{\frac{1}{12k^2}-1} \cdot
\qty(k\log n+1)^{\frac{1}{k}}
\\&\le& k\cdot \sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}
\end{eqnarray}
したがって
\begin{eqnarray}
\sum_{p\le n}\frac{1}{p} &<& \sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}(1+\log\log n)-1
\end{eqnarray}
となります。だいたい
\begin{eqnarray}
\sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1} \approx 2.80920417900466
\end{eqnarray}
ぐらいです。半分ぐらいになりました
最終的な下からの評価
長かったですが、以下の評価を得られました
自然数$n\ge 2$に対して、$n$以下の素数の逆数和について
\begin{eqnarray}
\sum_{p\le n}\frac{1}{p} < 2\sqrt{2\pi}e^{\frac{1}{12}}(1+\log\log n)-1
\end{eqnarray}
が成り立つ
特に、$n\ge16$の時は以下が成り立つ
\begin{eqnarray}
\sum_{p\le n}\frac{1}{p} &<& \sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}(1+\log\log n)-1
\end{eqnarray}
これで$D(n)$が評価できます。
\begin{eqnarray}
D(n) &=& D(m\#)
\\&=& m\# \sum_{p\le m} \frac{1}{p}
\\&<& n\qty(2\sqrt{2\pi}e^{\frac{1}{12}}\qty(1+\log\log m)-1)
\\&=& C_1n\log\log m+ (C_1-1)n \quad\qty(C_1=2\sqrt{2\pi}e^{\frac{1}{12}}\approx5.449)
\end{eqnarray}
とくに、$n\ge16$の時は
\begin{eqnarray}
D(n) &=& D(m\#)
\\&=& m\# \sum_{p\le m} \frac{1}{p}
\\&<& n\qty(\sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}\qty(1+\log\log m)-1)
\\&=& C_2n\log\log m+ (C_2-1)n \quad\qty(C_2=\sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}\approx2.8092)
\end{eqnarray}
と分かりました
ここで定理2より
\begin{eqnarray}
n = m\# &>& 2.22^m \\
\iff \log_{2.22}n &>& m
\\\iff \frac{\log n}{\log 2.22} &>& m
\end{eqnarray}
なので
\begin{eqnarray}
D(n) &<&Cn\log\log m+ (C-1)m
\\&<& Cn\log\log\qty(\frac{\log n}{\log 2.22})+(C-1)n
\\&=& Cn\log(\log\log n-\log\log2.22) + (C-1)n
\end{eqnarray}
となります。
へー
ちなみに$\log\log2.22\approx-0.22626442131$です
まとめ
平方因子を持たないかつ合成数な自然数$n\ge2$をとるとき、その素微分$D(n)$に対して、以下の不等式が成り立つ
\begin{eqnarray}
2\sqrt{n} < D(n) < Cn\log(\log\log n-\log\log2.22) + (C-1)n
\end{eqnarray}
ただし、
$n\ge2$のとき$C=2\sqrt{2\pi}e^{\frac{1}{12}}\approx5.449$
$n\ge16$のとき$C=\sqrt{2}\pi^{\frac{1}{4}} e^{-\frac{47}{48}}\sqrt{2e^2+1}\approx2.8092$
とする。
いえーい
グラフにするとこんな感じです
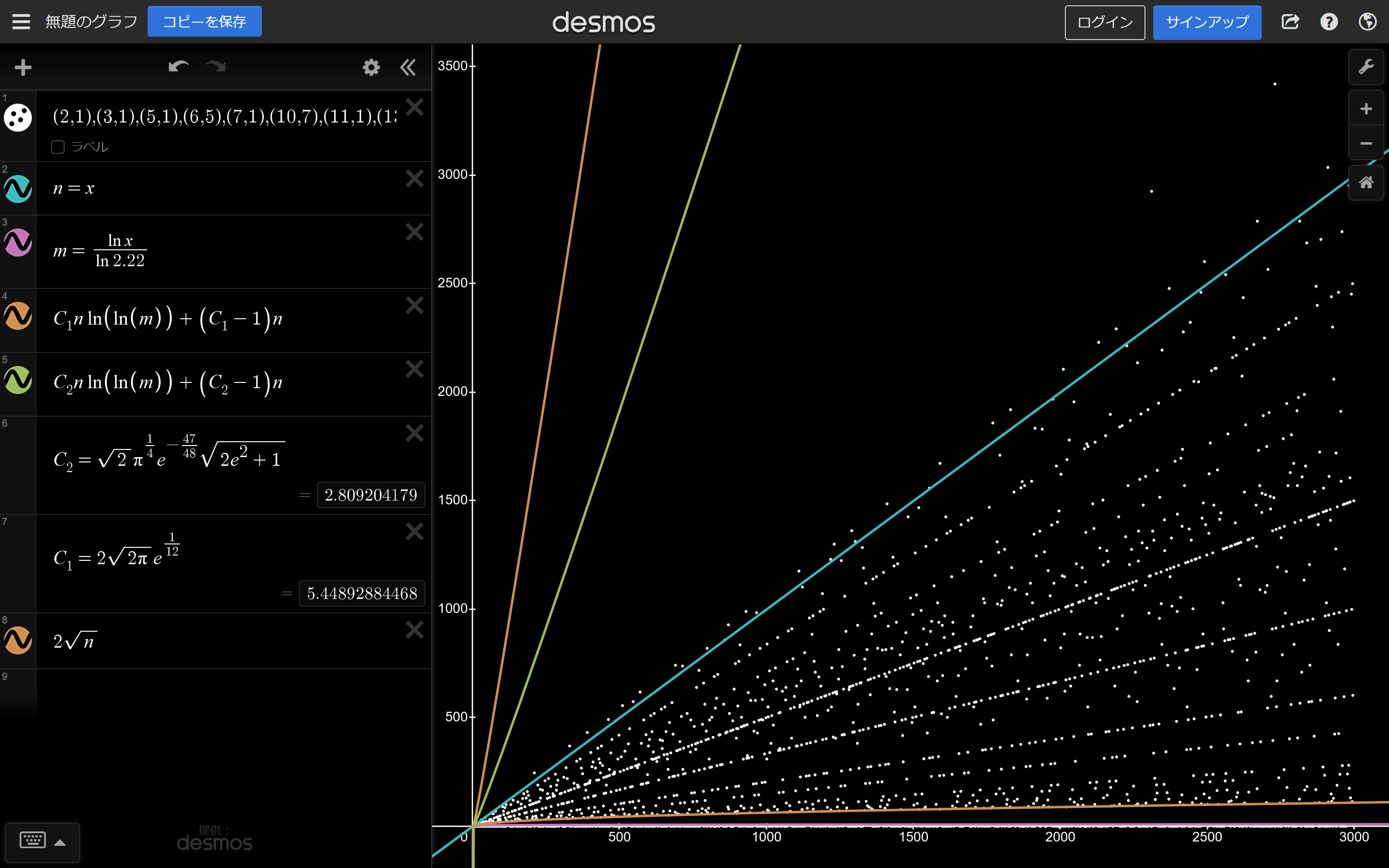
うーん...
Desmos
間違いが$\text{almost everywhere}$あると勝手に思っているので
もし見つけてくださったときはコメントしていただけると幸いです。
