埋め込み・はめ込み・沈めこみの具体例

　埋め込み・はめ込み・沈めこみ…多様体をやっていると見かけることも多いのではなかろうか？しかしどれがどの定義かごちゃごちゃしてしまうことが僕は多い．ここで各意味や具体例などをまとめてみよう．

定義など

　線形代数の復習をしよう．線形写像$h:V\rightarrow W$が全射であることの定義は$\Im h=W$であり，単射であるためには$\ker h=\{0\}$となるため，次元定理から$\dim V =\dim\Im h+\dim \ker h=\dim\Im h$となる．
　多様体の微分写像も線形写像のため，$f$がはめ込みとは$(df)_p$が単射であることを指し，$f$が沈めこみとは$(df)_p$が全射を指すことが分かる．
　また当然$f$がはめ込みであるなら，ヤコビ行列の階数が$m$にならないといけないこととヤコビ行列は$m\times n$なため，$\dim M=m\leq n=\dim N$であることが要請される．逆に$f$が沈めこみなら$\dim M=m\geq n=\dim N$が要請されるだろう．

意味など

　よくはめ込みと埋め込みの例として挙げられるのが次の写像だ．$f_1:S^1\hookrightarrow \mathbb{R}^2$が埋め込みであり，$f_2:S^1\rightarrow \mathbb{R}^2$を$\theta\mapsto(\cos 2\theta\cos\theta,\cos2\theta\sin\theta)$で定義すると，$\theta=\frac{\pi}{4},\frac{3\pi}{4},\frac{5\pi}{4},\frac{7\pi}{4}$で全て$(0,0)$に写るので埋め込みにならず，ヤコビ行列を計算すると
$$J_{f_2}=(-2\sin2\theta\cos\theta-\cos2\theta\sin\theta,\ -2\sin2\theta\sin\theta+\cos2\theta\cos\theta)$$
であり，これをベクトルだと思うと大きさを求めると，
$$\begin{array}{cl} & (-2\sin2\theta\cos\theta-\cos2\theta\sin\theta)^2 +(-2\sin2\theta\sin\theta+\cos2\theta\cos\theta)^2 \\ =& -12\cos^4\theta+12\cos^2\theta+1\\ =& -12(\cos^2-\frac12)^2+\frac34\ >\ 0 \end{array}$$
であるから0行列になることがないことが分かる．よって$f_2$ははめ込みである．
　$\rank(df)_p=1=\dim S^1<\dim \mathbb{R}^2$であるため沈み込みにはならないし，$S^1\rightarrow \mathbb{R}^2$では沈めこみを実現できないだろう．
$f_1,f_2$のグラフ
　なぜはめ込みというかというと，高次元の中に多様体を入れこむためだ．重複点でもヤコビ行列がフルランクならその地点での接平面が退化していないため，名前を付けているのである．図での二重点での接線を描いてみれば退化してないのが分かるだろう．
　埋め込みは重複点も無いため完全に多様体を実現するように空間に入れ込んでいると考えられるだろう．

　では沈めこみはどのような例があるか．トーラス$T^2=S^1\times S^1$に対して$f_3:T^2\rightarrow S^1$を$(\theta,\varphi)\mapsto \theta$を考えれば，ヤコビ行列を求めると，
$$J_{f_3}=\qty(\begin{array}{c} 1\\ 0 \end{array})$$
であるため$\rank(df_3)_p=1=\dim S^1$から沈めこみを得る．自明すぎてつまらないだろうか？ではこういうのはどうだろう．
　$T^2$の中にトーラス結び目を考える．つまり$T^2=(\mathbb{R}/\mathbb{Z})^2$と思って$\frac{m}{n}\in \mathbb{Q}$として$\{(x,\frac{m}{n} x)\ |\ x\in\mathbb{R}\}\in\mathbb{R}^2$を$(\mathbb{R}/\mathbb{Z})^2$に自然な全射$\pi$で写す．
$m=2,n=3$であるようなトーラス結び目
$p\in T^2$が$(\mathbb{R}/\mathbb{Z})^2$にあると考えて$[(p_1,p_2)]$で表示できるとしよう．トーラス結び目の終端は$[0,1)\times[0,1)$ が縦に$m$個，横に$n$個並べたときの一番右上である．
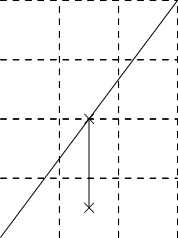トーラスの展開図
よって$p$は$(np_1,mp_2)$に対応する．これを利用して$(np_1,\frac{m}{n}\times np_1)$を取って自然な全射$\pi$で写した写像$f_4$は$T^2\rightarrow S^1$となる．このとき一周分になるときは，正方形を敷き詰めたときの右上になるから長さが$n^2+m^2$である．これに対してスケールを調節する$a:S^1\ni np_1\mapsto \frac{2\pi}{n^2+m^2}\times np_1\in S^1$を考えれば$a\circ f_4=f_3$とできる．$a$は定数倍であるから微分同相でヤコビ行列は可逆であるためランクを保つ．
$$J_{f_4}=(J_a)^{-1}\times J_{f_3}$$
であるため，$\rank (df_4)_p=\rank(df_3)_p=1=\dim S^1$から沈めこみになる．

　まとめると，トーラスからトーラス結び目への沈めこみがあるということだ．$f_3$はトーラス結び目の特別な場合だ．

　なぜ沈めこみか．高い次元のものを低い次元に入れ込んでいるからだと考えている．高い次元の多様体が低い次元の多様体にﾇﾑﾎﾞﾎﾞﾎﾞと沈んでいくのを想像すればいいのかもしれない．

具体例

ここでははめ込み・沈めこみにならない例を見てみよう．どのような点のせいではめ込み・沈めこみが消えてしまうのか見ていこう．

1. $\mathbb{R}\rightarrow\mathbb{R}^2$の場合

・$\dim\mathbb{R}<\dim\mathbb{R}^2$より沈めこみにはならない．はめ込みでない例としてアステロイド$g_1:S^1\ni\theta\mapsto(\cos^3\theta,\sin^3\theta)\in\mathbb{R}^2$を考える．
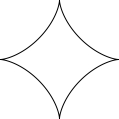アステロイド
　これのヤコビ行列を計算すると
$$\begin{array}{rcl} J_g &=& (-3\cos^2\theta\sin\theta,3\sin^2\theta\cos\theta)\\ &=& 3\sin\theta\cos\theta(-\sin\theta,\cos\theta) \end{array}$$
であるから，$\theta=0,\frac{\pi}{2},\pi,\frac{3\pi}{2}$のときのせいではめ込みにならない，これは尖点のときである．

2. $\mathbb{R}^2\rightarrow\mathbb{R}^3$の場合

・Whitenyの傘を表現する$g_2:\mathbb{R}\ni(u,v)\mapsto(u,uv,v^2)$というものを考えてみよう．
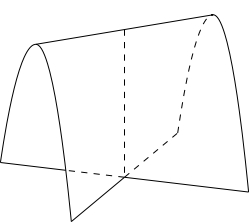Whitneyの傘
これのヤコビ行列を計算してみると
$$J_{g_2}=\qty(\begin{array}{ccc} 1 & v & 0\\ 0 & u & 2v \end{array})$$
であるから，$u=v=0$のときがはめ込みでなくなる．ちなみに$u=0$は二重点軌跡であり，埋め込みであるような点でないが，はめ込みであることがヤコビ行列の計算から分かる．

・正方形の向かい合った辺を反対向きに張り合わせた図形を射影平面という．
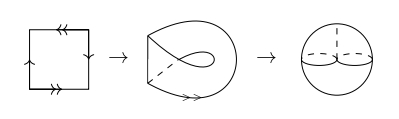射影平面
この射影平面には二つのWhitenyの傘をもつが，先の計算からはめ込みでないことが分かる．

・ついでにトーラスとKleinの壺についても触れておこう．それぞれ正方形の対辺を張り合わせることで実現できる曲面である．トーラスは二組とも向きを同じに張り合わせる．Kleinの壺は一つの対辺の組を同じ向きで，もう一つの組は向きを変えて張り合わせたものである．
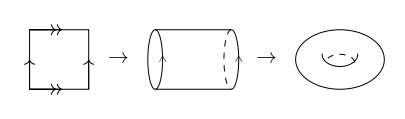トーラス
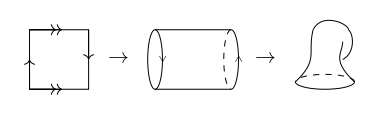Kleinの壺
　トーラスは二重点や接平面が退化している点が無いので埋め込みになる．正確には正方形$\mathbb{R}^2$から空間$\mathbb{R}^3$への写像と考えられる．Kleinの壺は接平面が退化しているような点はないが，二重点の軌跡はあるのではめ込みである．

3. $\mathbb{R}^2\rightarrow \mathbb{R}^2$の場合

この場合ははめ込みも沈めこみにもなり得る．
・まず$g_3:\mathbb{R}^2\ni(u,v)\mapsto(u,-uv+v^3)\in\mathbb{R}^2$を考えよう．
$g_3$の定義域と像
これのヤコビ行列を計算してみると
$$J_{g_3}=\qty(\begin{array}{cc} 1 & -v\\ 0 & -u+3v^2 \end{array})$$
となるため$-u+v^2=0$となる軌跡があるためはめ込みにならない．
　ちなみに$g_4:\mathbb{R}^2\ni(u,v)\mapsto(u,v,-uv+v^3)\in\mathbb{R}^3$を経由し$\pi_2:\mathbb{R}^3\ni(x,y,z)\mapsto(x,z)\in\mathbb{R}^2$を合成したものを考えれば$\pi_2\circ g_4=g_3$となるが，
$$g_4=\qty(\begin{array}{ccc} 1 & 0 & -v\\ 0 & 1 & -u+3v^2 \end{array})$$
であるため，二重点でもないから埋め込みである．それを射影$\pi_2$で写すことで特異点が現れる．

・沈み込みも考えてみよう．$S^2=\{(\cos\varphi\sin\theta,\cos\varphi\cos\theta,\sin\varphi)\in\mathbb{R}^3\ |\ \theta\in[0,\pi],\varphi\in[0,2\pi]\}$としてみよう．$\pi_2$を考えれば，$\pi_2:S^2\ni(x,y,z)\mapsto(x,z)\in\mathbb{R}^2$は$S^2$の座標を使って
$$\pi_2(\theta,\varphi)=(\cos\varphi\sin\theta,\sin\varphi)$$
と表せる．
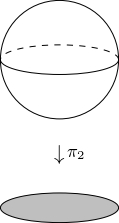球の影
これのヤコビ行列を計算すれば
$$J_{\pi_2}=\qty(\begin{array}{cc} \cos\varphi\cos\theta & 0\\ -\sin\varphi\sin\theta & \cos\varphi \end{array})$$
となりこれのランクが落ちる条件は，行列式が0なる条件を求めればいい．
$$|J_{\pi_2}|=\cos^2\varphi\cos\theta=0$$
より$\theta=\frac{\pi}{2},\frac{3\pi}{2}$で$\varphi$が任意か$\theta,\varphi$が逆になったものだ．これの軌跡を$S^2$の座標から求めると，$(\pm\cos\varphi,0,\varphi,\sin\varphi)$か$(0,0,1)$であるため，$xz$平面にある大円である．

　つまり端っこの影の部分で沈めこみになっていないことが分かる．確かに像の接平面を考えれば影の内部は2次元分あるが境界部分は1次元分しかないため退化していることが分かる．

4. $\mathbb{R}^2\rightarrow\mathbb{R}$の場合

この場合ははめ込みにならないため沈めこみだけ考えよう，
・円の高さ関数を考えてみよう．$g_5:S^2\in(x,y,z)\mapsto z\in\mathbb{R}$とする．
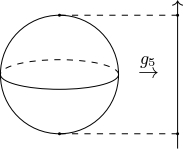球の高さ関数
球の座標を使えば$g_5(\theta,\varphi)=\sin\varphi$であるから，これのヤコビ行列を計算してみると
$$J_{g_5}=\qty(\begin{array}{c} 0\\ -\cos\varphi \end{array})$$
であるからランクが落ちる条件は$\varphi=\frac{\pi}{2},\frac{3\pi}{2}$であるため$(0,0,1),(0,0,-1)$が沈めこみでない点だ．

Whitneyの埋め込みはめ込み定理

　実は多様体は高次元のユークリッド空間であれば埋め込める・はめ込めるという定理がある．

　この定理には本当は埋め込み・はめ込みでない写像は少し動かしたら埋め込み・はめ込みになるということが本当は大事なのだがそれは別の話だ，
　また$N\geq2n-1$に対してはWhitneyの傘を許容すればはめ込みが稠密に作れるという定理もある．これを実際に例でみて確認してみよう．二次元平面射影平面は2次元多様体であるが$2\times2-1=3$次元ではWhitneyの傘が現れることが先ほどの例から分かる分かる．ちなみにWhitney trickを使ってこのWhitneyの傘を消すこともできる．

Ehresmannの補題

fibrationというものを導入しよう．例えば直線$\mathbb{R}$に対してアニュラス$S^1\times \mathbb{R}$を考えれば写像$\pi:S^1\times\mathbb{R}\ni(p,x)\mapsto x\in\mathbb{R}$が次を条件を満たす．
局所自明化条件：$^\forall p\in \mathbb{R},\ p\in^\exists U\subset \mathbb{R} \text{：open nbh.},\ \pi^{-1}(U)\overset{\text{diffeo.}}{\approx} U\times S^1$
$S^1$をfiberと言い，それをfiberとするアニュラスをfibrationと言う．$S^1$とアニュラスを一般の多様体に変えることもできる．この$\pi$は沈めこみになっている．
　逆に沈めこみがあれば潰れている場所，つまり$\pi^{-1}(p)$をfiberとする定義域がfibrationになってそうだ．しかし無条件にはなってなさそうである．こういう思い付きは大抵誰かがやっているので調べてみればいいだろう．「沈み込み　ファイブレーション」と調べると，Ehresmannの補題というものがヒットする．それを理解するためには固有写像というものが必要になる．

　例えば$f_4$なら$\mathbb{R}$の任意なコンパクト集合$I$は有界閉なのでその引き戻しを考えれば，トーラス内の有界閉集合に写る．正確には$ I\times S^1\subset T^2$になるため，$f_4$は固有写像である．
　もう一つ，固有写像にならない例を見てみよう．$p\in S^1$を取り，アニュラス$S^1\times \mathbb{R}$から一本線を抜いた$S^1\times\mathbb{R}\ \backslash\ \{p\}\times\mathbb{R}$を考えるそこからの写像$h_1:S^1\times\mathbb{R}\ \backslash\ \{p\}\times\mathbb{R}\ni(x,y)\mapsto y\ni\mathbb{R}$を考える．一点集合$\{0\}$は有界閉集合なためコンパクトである．$h_1$は連続写像ためその引き戻しを考えると$S^1\backslash\{p\}$であるがこれはコンパクトでないため$h_1$は固有写像でない．
　ではようやくEhresmannの補題を紹介しよう．

　例えば，この定理を使えばトーラスは$f_4$を用いて，トーラス結び目に沈み込ませればファイブレーションになることが分かる．つまりトーラス結び目を積層させればトーラスが出来上がるのだ．$S^1$なら自明だがトーラス結び目なら少し想像がしがたいだろう．
　展開図を使えば幾分理解がはかどるかもしれない．
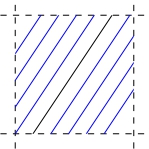トーラス結び目のFibration