数学オリンピック体験記2023
お久しぶりです. 現役としての最後のコンテストが終わったので, 去年の記事 以降数オリに向けてしたことや感想を備忘録を兼ねて記そうと思います. 早速行きましょう!
分野について
- A $\cdots$ 代数. 本選以降はさらにFE(関数方程式), 不等式, その他と細分化される.
- C $\cdots$ 組み合わせ
- G $\cdots$ 幾何
- N $\cdots$ 整数論
- P $\cdots$ 問題
コンテストなどの略称
- JMO $\cdots$ 日本数学オリンピック
- JJMO $\cdots$ 日本ジュニア数学オリンピック
- IMO $\cdots$ 国際数学オリンピック
- APMO $\cdots$ アジア太平洋数学オリンピック
- TST $\cdots$ team selection test 代表選考テスト
- ISL $\cdots$ IMO shortlist
- 春合宿 $\cdots$ 3月下旬の代表選考合宿
- 初夏合宿 $\cdots$ 5月上旬の代表強化合宿
本の略称
- パフェマス $\cdots$ ○○パーフェクトマスター/日本評論社
- 獲得 $\cdots$ 獲得金メダル! 国際数学オリンピック メダリストが教える解き方と技/朝倉書店
- EGMO $\cdots$ Euclidean Geometry in Mathematical Olympiads/MAA Problem Book Series
- 船旅 $\cdots$ 数学オリンピック幾何への挑戦 ユークリッド幾何学をめぐる船旅/日本評論社
内容はあくまで一個人の意見として軽く受け止めてください!
夏季セミナー
コンテスト中心のいわゆる数学オリンピックとは少し離れていますが, 数学オリンピック財団主催で8月の下旬に山梨県の清里に集まって純粋数学の書籍を輪読するセミナーです. 春合宿参加者, ヨーロッパ女子数学オリンピック日本代表は希望すれば無条件で, そうでない人もレポート提出で参加できるチャンスがあります!
本当に楽しくて刺激的なので皆さんぜひ参加しましょう!ただの宣伝です.
~予選
前年度で本選を通過すると予選は無条件で通過となるため, 今年は本選以降の記述問題の対策をメインで行いました. ただ, 予選免除の有無に関わらず, 記述問題は早い段階から積極的に取り組みましょう!!
というのも,
- 実は予選から本選まではほとんど時間がない
- 短答式特有のAd-hocな解法を積むより, 記述で普遍的なテクニックや感覚を身につけるほうが結果的に効果的な予選対策になる
- 何より競技数学人生を記述の問題に十分に触れることなく終えるのはあまりにももったいない!
からです. さて, 主に取り組んだ問題は
- 整数問題bot(@seisu_bot)
- IMO shortlist
- その他TST
です. こう見ると, ほとんど整数かISLしかしてなかったんですね().
整数問題bot
夏休みくらいから取り組みはじめ, IMO直前くらいまでに自力で全問題埋めました. 問題は全部で240問程度.
メリット
- 難易度が幅広く対応しており, 難易度の表記もしてある
- 様々なタイプの問題を扱っているのでテクニックを満遍なく身につけられる
- これだけの問題量の整数問題を網羅的に挙げているのはほかに知らない
デメリット
- 解答がない問題がそこそこある!
- 難易度がたまに大きくずれている(ちなみに, 「やや易」は全く絶対的な意味での「やや易」ではないので, 問題同士の相対的な難易度評価のものさしに使うのが無難です)
予選突破が目標なら簡単なほうから, 予選突破ができたら「易」くらいから, 本選突破もできていたら「やや易」以降の全埋め目標とかが目安だと思います.
ISLについては
ここ
に書いています!
あとは去年のまとめノートは今年もずっと継続しました. 途中からはスマホのメモをメインで使っていました.
 めも
めも
 メモの中身
メモの中身
こんな感じです. 数オリの対策の中で一番効果があった気がします.
ポイントとして上のメモを見ると分かるように, 単なる解法暗記ではなく, 「〇〇を見たら〇〇」といったように なぜその発想が出てくるかといったモチベーションを大切にすることです.
解いた問題一問一問, その問題の本質は何か, どこが非自明ステップか, そのステップはどんな応用が利くか, どうやったら自然な発想に思えるかを丁寧に考えるのって意外と楽しい作業ですよ. 個人的にはこれが一番数学を楽しめつつ力もつく取り組み方だと思っています.
話が少しそれましたが, こんな感じでひたすら問題を解いていました. あとはOMCもできる限り出ていました!
予選前までにはISL(2011~2020)は
Aは4まで全部+5以降のFE中心に,
Cは4まで大体+5以降数問
Gは5まで大体
Nは5まで全問?+3番級何問か
を解いていました.
思い出したので追記なのですが, 射影幾何の完全理解にも挑戦してみました. EGMOなどでは証明が省略されていたりするので, ベクトル空間から射影平面を構成して, 各定理を証明してみました. これはいい気分転換かつ数オリで射影を使うことに対する抵抗が大きく減ったので, して良かったと思っています. これについてはいずれ記事を書くかもしれません.
予選
この章はJMO2023予選の問題のネタバレを含みます!
始まる前はあみのとまいんと(たしかじよ君も)早稲田のマクドナルドで昼食を食べました. 美味しかったです.
予選は全完が目標でした.
とりあえず最初から解いていきます. 予選は実験をするか式におくことで本質が見える問題が多い気がします.
1~6を解いて23分経過
7, 8も解いて40分経過
9を解いて50分経過
10を解いて82分経過
11がなかなか解けません...いったん飛ばして12を考察.
143分で12の答えらしきものが出ました. ここで一度解いた問題を全部見直しました. 見直しは, 計算をもう一度行う, 別の方法で解いてみる, 図を正確に書いて妥当性を確かめる, 解答形式を確かめるという感じです. その結果ミスを3問見つけたので本当に見直しは大事です!
結果は12345678912の10完でした. 10で計算ミスをしていたのでやっぱり見直しは大事ですね!()
予選~本選
予選通過は確定していたので, 今まで大体通りの対策を続けていました. 一つだけ変わったことといえば, 本選も全完が目標だったので, P4やP5の過去問を友達と通話しながら解きました. 2007P5や2017P5はかなり好きな問題でした.
また, 本選直前に重心座標を一夜漬けしました. 目に見える効果はありませんでしたが, 後悔をしたくないというのが大きかったです.
本選までにISL(2011~2020)は302問中ちょうど200問を自力で埋めていました.
本選は分野によっては大事故が発生するので, 春合宿より緊張していました.
本選
この章はJMO2023本選の問題のネタバレを含みます!
始まる前はあみのとまいんと(たしかdentaも)早稲田のマクドナルドで昼食を食べました. 美味しかったです.
本選も全完が目標です. 分野はCGANA, 34にC, G, 不等式がなかったので見た瞬間4完を確信しました.
10分経過, P1を書き終える. JMOP1の敷き詰めは大体色塗りの印象.
50分経過, P2をなんとか... 幾何が圧倒的にできないので迷走に迷走を重ねました. この問題, 実は直前にセット予想をしていて, 幾何の初手を「回転相似」と予想したらそれが見事的中していました. それがなかったら今の自分はいないので, セット予想はした方がいいです(強めの主張).
95分経過, P3を書き終える. 去年身につけた, 答えが出る前に答案を書き進めながら添削していく方法で解きました. 分かったことが綺麗に整理されるのはすごく良いです.
135分経過, P4を書き終える. N4でこのタイプの問題はできることも少ないので, できそうなことやわかることを試していけば確実に進捗が生まれます. $\varphi$の乗法性やLTEは証明なしでも減点されませんでした.
さて, P5. 自明な下界と上界を出して以降全く進展がありません.
結局そのまま240分経過.
結果は88781の32点, 銀メダルでした. FE, 数列の十分性の確認は絶対しましょう!!!
これでメダルの色が一色落ちるとかなり萎えます. また, IMO2022P2みたいな十分性が非自明な問題もあるので, 思考放棄で十分性okと書くだけでなく, ちゃんと確認をしましょう!
予選本選共通して, コンテストを楽しむくらいの心の余裕があると案外結果はついてくるものです.
本選~春合宿
本選通過の手ごたえはあったので, そのまま対策を続けました.
数オリからは少し逸れるのですが, ちょうど科学の甲子園全国大会が春合宿直前に控えており, その準備で数オリの対策はあまり思うようにできませんでした. 対策は今までと大きくは変わりませんが, ISLのGの比重を大きくしました.
たいていの場合春合宿は1番級, 2番級をどれだけ安定して解けるかの勝負です. 少なくとも本選や春合宿前は苦手分野をつぶすことを優先することを強くお勧めします.
APMO
この章はAPMO2023の問題のネタバレを含みます!
去年は全然入賞に届かなかったため体験記ではスルーしましたが, 今年は金賞を頂けたので, 少し言及します. 試験は4時間5問, 難易度はかなり幅があり, しかも難易度順でないことも多々あります.
](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FjtKTKTidDEjrDf0hmCek.jpg?alt=media) APMO2023
APMO2023
APMOは唯一IMOに直結しないコンテストなので, 自分の好きなように取り組めます. 特に具体的な目標は決めていませんでしたが, 全完できたらいいなと思っていました.
分野はCNGAC, APMOは難易度感が本当につかめないので, とりあえず最初から進めていきます.
P1. 構成を頑張ればよさそう. $n$の増加で自由度が増えていくタイプの問題で一般の構成をするときには, 最初に大きいものを処理してから残りで細かい調整をするとうまくいくことが多いです. この問題もそれで行けました.
P2. シンプルな不定方程式なので, できることを片っ端から試していきます. 大小のイメージをつかむと, $\sigma(n)$は$n(p(n)-1)$に比べて増加速度が同じくらいか小さそうです. 具体的には$\sigma(n)$を素因数で書き下して評価すればok. これは整数問題bot148での知見です.
シビアな評価が出てきたら, どこでその評価が崩れるのかを考えれば, $n$を絞れそうです. これも比較的スムーズに行けました.
P3. 何これ. 少しだけ考察をしますが, あまり進展が生まれない. 逆が自明なので, 何らかの単調性について注目することで示せるというテクニックがあるので, 刺さりそうですがいまいちうまくいきません.
一旦P4に行きます. $\mathbb{R}_{>0}$のFEでしかも謎の$c$が登場しています. $\mathbb{R}_{>0}$の典型は一度研究してみたので, 片っ端から試すと少し頑張って単射が言えました(が結局使えなかった). 最終的に, $f(x)\ge2x$が言えて$f(x)=2x$が解だったので別の典型として抑えていた$g(x):=f(x)-Ans$の再定義を試してみると, $g(x)$の有界性みたいな議論に帰着されなんとか解けました. 純粋FEはできることがかなり限られるので, 対策が威力を発揮する印象です(最近は頻度が減ってきている印象だが).
P3を飛ばしてP5に行きます. 片側の評価は手を動かしたら思いつきました. ですが, もう片側はなかなかできません... ここで残り1時間. 少し焦りが生じます.
P3に戻って手を動かしてみると, いい感じの単調性が見つかりました!なんとかギリギリで答案を書き終えました.
結果は77772で金賞. 全体的にどれだけ経験値を積んできたかみたいなセットな感覚でした. ただ, APMOとIMOの結果は本当に全然相関がないので, 大事故を起こしてもあまり落ち込みすぎないことです.
春合宿
この章は春合宿2023の問題のネタバレを含みます!
いよいよ迎えた春合宿. 試験前日まで科学の甲子園だったので疲労がかなり蓄積していました. 目標はもちろん代表になること. ずっと会ってみたかった人が何人かいたのですごくテンションが上がりました! それもあって, 試験はかなりリラックスした状態で受けられました.
試験は4時間半を4日間, 1問7点を計12問です.
Day1
P1. $n$を$d(n)\ge4$なる正の整数とする. 正の整数からなる等差数列$a_1, a_2, \cdots, a_{d(n)-1}$であって, 任意の$1\le i\lt j \le d(n)-1$なる整数$i, j$に対し$\gcd(a_i, n)\neq\gcd(a_j, n)$なるものが存在するような$n$を全て求めよ.
P2. $1$辺$2023$の正方形のマス目に, 縦横$1012$マス, 計$2023$マスのL字型は最大何個入るか.
P3. $n$個の実数$a_1<\cdots< a_n$と実数$r>0$であって, 各$1 \le i< j \le n$についての$\dfrac{1}{2}n(n-1)$個の差分$a_j-a_i$が$r^1,r^2,\ldots,r^{\frac{1}{2}n(n-1)}$のいずれかの順番になるようなものが存在する$n \ge 2$を全て求めよ.
分野はNCA. 2完は死守してあわよくば全完したい分野でした.
P1を考え始めます. IMOしかり最近この手の問題すごく多いですね. 真っ先に素因数ごとの議論をしてみますが, 無限に場合分けが発生します. 一つひとつ丁寧に処理していきましたが, 絶対漏れや議論ミスがありそうという感覚. 1時間ちょっとくらいで解答を書き終え, P2に行きます.
とりあえず解の予想をしてみる. 端から詰めていくと1012枚入るので, 多分評価が大変な感じの問題. しかし, 中々進展がありません. L字の直角の部分を「中心」と呼ぶと, 1013枚以上入れるときには中心は真ん中の行や列に来ないということしかわかりません. ずっと同じところを行ったり来たりしているだけだったので, 一旦2023を7にしてめちゃくちゃ実験を重ねると...なんと5枚入っちゃいました. !?
当時は全く想像していなかったのですが, 最初の予想を疑ってみるのはときに大事なんですね.
少し余談ですが, C分野とかで実験をするときには下みたいな表をよく作っています.
| $n$ | min(構成) | Max(評価) | Ans |
|---|---|---|---|
| $1$ | $1$ | $1$ | 1 |
| $2$ | $2$ | $2$ | 2 |
| $3$ | $2$ | $3$ | ? |
| $4$ | $3$ | $4$ | ? |
| $k$ | $k/2$ | $k$ | ? |
今の進捗や方針が見えやすくなってすごくおすすめです.
......
と同時に評価の方もいい感じに見えたので, 解答が$2023\times\dfrac23$くらいだと分かりました. 2Cが解けると少し安心します.
P3を考えますが, 一見よさそうな方針に固執してしまい, 行き詰まったまま時間切れとなってしまいました.
結果は672. やっぱりP1は漏れがありました. 無理ですあれは.
去年と違い, すでに1完も2完もいました.
やっぱり4時間半3問のコンテストは過酷で, その一方で解けたときの気持ちよさも並大抵のものでなくて, 本当に楽しいです.
Day2
P4. 鋭角三角形$ABC$について, $F$を$A$から下ろした垂線の足, $P$を線分$AF$上の点とする. $P$を通り$AC$と$AB$に平行な直線が$BC$とそれぞれ$D$, $E$で交わっている. 点$X \ne A$と$Y \ne A$をそれぞれ円$ABD$と円$ACE$上に取ったところ, $DA = DX$および$EA = EY$が成立した. $B, C, X, Y$の共円を示せ.
P5. 任意の実$x,y\in\mathbb R$に対して数以下を満たす関数$f\colon\mathbb R\to\mathbb R$を「良い関数」と呼ぶ(違ったかも).
$$f(x + f(y)) = f(x) + f(y)$$任意の良い関数$f$に対して, ある実数$z$が存在して$f(z) = qz$となる有理数$q$を全て求めよ.
P6. 各整数$1\leq i\leq 9$と$T\in\mathbb N$に対し, $d_i(T)$を$1829$の$1$倍から$T$倍まで十進法で書いたときに桁に登場する$i$の総数とする.
$d_1(T)$, $d_2(T)$, $\dots$, $d_9(T)$の中にちょうど$2$種類の値が登場するような$T\in\mathbb N$が無限に存在することを示せ.
分野はGAN. 全完できれば大きなアドになるのでそれを目標にしました.
1Gは沼ると大変なので, 少し緊張します. 最終的に方べきで倒すのがイメージできたので, そこから逆算すればいい感じの補助線を引くことができました. 30分くらいで無事討伐.
P5はこの形のFEをELMOで見たことがあったので, 絶対いけるという気持ちになりました(実は単調性をつけると解を明示的に書ける). しかし, 解の構成が全然できません!!途中Hamel基底を取るとかいう迷走もいいところです. P6を少し考えますがこっちも全くわからない. ものすごく焦りました.
構成をもう少し頑張ってみると, 像が$\mathbb{R}$の部分加群$M$になるので, $\mathbb{R}/M$の代表系での値を($M$の中から)決めれば全体に一意に拡張できることを発見します. 特に$M$を$\mathbb{Z}$にすればいい感じです(逆の議論は$M\neq0$のとき$M$の部分加群で$\mathbb{Z}$と同型なものを取ろう). これは実際この問題の本質ポイントで, 解答に直結できました. 好き.
P6は結局解答につながる進捗は埋めませんでした. これも余談ですが, 生年月日が平成18年2月9日だったので何か運命的なものを感じたのですが, 1829は別に3でもよかったらしいです...
結果は750. P5は計算ミスをしていました. 悲しい...
3Nをこの問題で消費してしまうのがかなり残念です.
また, この頃3番級への先入観が解くことの障害になっていることに薄々気づいたのでした(詳しくは後述).
Day1, 2で自称5完↑は0, 自称4完も聞いた中では5人くらいしかいませんでした.
あと2日で事故らなければ代表になれそうな気がなんとなくしていました.
Day3
P7. 「$\pm 1$-数列」を$2022$項からなる数列$a_1, \ldots, a_{2022}$であって各項が$+1$あるいは$-1$であるものとする. 任意の$\pm 1$-数列に対し, 正の整数$k$と添え字$1 \le t_1 < \ldots < t_k \le 2022$が存在し, 任意の$i$に対し$t_{i+1} - t_i \le 2$, かつ$\left| \displaystyle\sum_{i+1}^{k} a_{t_i} \right| \ge C$となる最大の$C$を求めよ.
P8. 日本オリジナルのN, 問題が異様に長かった. $\mathbb{F}_p$で操作をする問題
P9. $ABC$を垂線$AH$を持つ鋭角三角形とし, 点$P$が, $\angle PBC$と$\angle PCB$の二等分線$k$と$\ell$が線分$AH$上で交わるように動く. $k$が線分$AC$と$E$で交わり, $\ell$が線分$AB$と$F$で交わり, 線分$EF$と線分$AH$が$Q$で交わる. $P$が動くとき, 直線$PQ$はある定点を通ることを示せ.
分野はC?NG. この日は何と問題文が裏面までありました(!?). 去年のDay3があったので嫌な予感しかしません.
P7はまず実験をすると, $1$の部分は全部回収して$-1$の部分は一個飛ばしとかで評価が回りそうです. 構成は, この評価が一番シビアになる条件を考えれば行けます.
そしてP8, ゲームの問題で問題文が本当に長い, 下手したら去年のP8より長いかもしれない. よく分からないけどとりあえず不変量を構成したくて, 不変量を構成したら一瞬で行けました. すこし嫌な気分になりました.
P9はGだったので, 計算で無理なら無理だと思っていました. しかし, 問題文を読み進めていくと「直交座標で解け」という強い意思を感じたので, 直交座標で頑張ります. すると, 1時間くらいで解けてしまいました. かなり呆気なかったです.
数オリのコンテスト初の全完だったので, めちゃくちゃテンションが上がっていました!
残りの1時間半くらいはP8を主に推敲したり, お菓子を食べたりしていました.
結果は776. P9は微妙にコーナーケースを落としていたみたいです. この日はまいんも全完していて, 話した人では2完が一番多かったです.
Day4最悪0完でも通りそうとはいえ, 去年より易化したのも事実なので, 油断できない状況でした. Day4の2Gは確定なので, 怖かったです.
Day4
P10. $k\ge2$を整数とする. 相異なる$n$個の実数からなる集合であって, 各要素が$k$個の他の相異なる要素の和として表せるものが存在するような最小の整数$n \ge k+1$を求めよ.
P11. 日本オリジナルのG, 覚えていない.
P12. 日本オリジナルのC, グラフの問題. 覚えていない.
問題全然覚えていなくてすみません.
分野はAGC, 全完はほぼ間違いなく無理なので2完死守が目標でした.
P10は実験の段階で, 最初$n+O(1)$か$2n+O(1)$か微妙でしたが, $n=5$くらいまで頑張ると$n+4$っぽそうというのが評価構成同時に出てきました. 先ほどの表も活躍しました. 30分くらい.
問題のP11です. 2Gに対する苦手意識が大分あったので, 緊張しています. そして...解けない, なぜか解けない. 計算も反転も何もささらない. 本当に何も進捗がない. 4時間椅子を温めて, 終ったあとは絶望していました.
結果は710. 結果として代表ボーダーは大きく超えていたわけですが, 最終日1完というのは本当につらかったです.
こんなわけで, 春合宿が終わりました. 現役引退が少しずつ近づいてきます.
春合宿~IMO
春の手ごたえからして, ほぼ通っていることは確信していたものの, 科甲→春がひと段落して, 去年に勝るとも劣らない虚無を感じていました.
4月1日の午前, まいんからの連絡で代表になったことを知りました. 嬉しさよりも安心のほうが大きかったです.
3番級への向き合い方
去年みたいに, 自分に足りないものを一度考えました. やはり3番級です. 2番級までは体感9割くらいの問題を時間内に解けましたが, 3番級の壁は大きかったです.
ISLも3番級を中心に解くようにし(結局本選以降自力で解けたのは9問だけだったが), それらとの向き合い方に対する葛藤を重ねました.
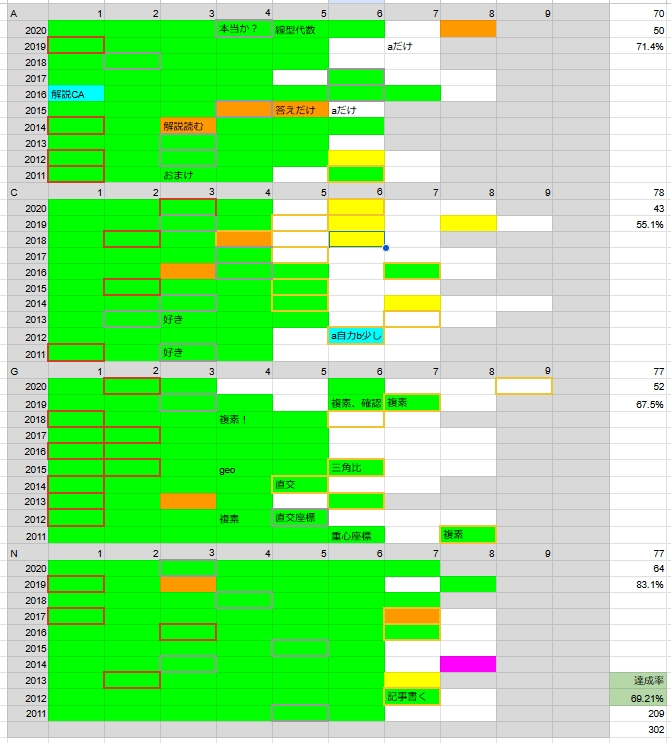 直前の進捗 緑は自力CA, 橙は解説見た, 水は解説CA, 黄色は挑戦中
直前の進捗 緑は自力CA, 橙は解説見た, 水は解説CA, 黄色は挑戦中
また, さっき少し言及したように, 3番級は3番級という先入観だけで解くことを拒んでしまう, 正常な考察の手順を踏めなくなってしまうということにずっと悩んでいました. 上の画像みたいに3番級を何十問も解いてなお, です. 去年は成功体験がなかったから解けなかったと思っていたけれど, 話はそこまで単純ではなかったようです.
それを克服するために今年は次のことをしてみました.
- もちろんできる限り多くの成功体験を作る.
- 3番級を最初に少し考察する(リスクが高いので本番はNが来た場合に限ると決めた).
- とにかく解けると言い聞かせる. 本番は財団やチューターの方に事前に「今年の3番級は簡単らしいよ」と言ってもらうようにお願いした.
できる限りのことはしました.
IMOに向けた対策
ISL3番級に加えてしたことは,
- 整数問題bot全埋め
- 友達と問題共有
の二つくらいです. 実際整数問題bot全埋めは, ものすごく大きな自信になりました. 後者は, 教育的な問題を共有することで, 苦手分野を主に克服しました.
しかし, 添削や受験勉強, 学校行事, (整数コン開催, )で想像以上に時間を取られてしまい, 思うように対策が進みませんでした. そのせいか何回かモチベーションの波が来ました. 最終的にIMOで極大となったのは不幸中の幸いだったかもしれません.
こんな感じで, 最終的にAは~2.5番級, C, Gは~2番級, Nは~3番級まではほぼ安定して解けるようになりました.
IMO
この章はIMO2023の問題のネタバレを含みます!
今年は日本開催で, さらに直前に期末考査があったこともあり, 去年以上に実感がありませんでした.
東京駅のマクドナルドであみのとまいんと昼食をとりました.
去年同様, コンテストメインで書きます.
目標は全完でした. 去年の沖さんに対する憧れは大きく, 自分もどこかそうなりたいと思っていました. しかし, そのためには3番級がNとA, かつ2番級が難しくない必要があり, 運との勝負でした.
Day1
](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F24PgOeYn0fjAeDMqzrcc.jpg?alt=media) Day1
Day1
分野はNGA. ギリギリ及第点です. 一番恐れていた2Gが初日で来てしまい, 緊張が走ります.
P1, Nです. やっぱり最近多いですよねこんな感じの問題. これは一瞬で片づけたいと思いました. 約数っぽい問題の実験は
素数→素べき→$pq$→$p^nq$や$pqr$→一般
みたいにやると本質が見えやすいことが多いです. 今回は素べきで回り, $pq$の場合だと最後$p, q, pq$でバグります. これと同じ感じでいきたいので, $p^nq$で約数が大きいほうから見ていくと, $n/q$のあたりでバグるので, 答案にします. 小さいほうだけに固執すると沼りそう. この問題に限らず, 今している操作の真逆の操作をすることは常に念頭に置くことをお勧めします. もう一方の試していない方を試すと意外と一瞬で終わることがあります!
15分くらいで解き終えました.
P2, Gです. 図が非対称. そのままだと計算は無理そうなので, まずは初等的考察をします. まず$P$の分かりやすい特徴づけをしたいですね. その結果, $\omega$と$AE$の交点$X$を取ると劣弧$BC$の中点$T$について$TXP$が共線とわかるので, いい感じ. あとはangle-chaseで接線を特徴づけて, 複素に突っ込みます. 示すべき式を一回間違えて沼りましたが, 結果2時間残して解答. モチベーションは常に意識しておきましょう.
P3, A. 見た瞬間「行ける!」と確信しました. というより強制的に自己暗示をかけました.
解答用紙を一枚とり, 半分に区切り, 片方に「したいこと」もう片方に「分かったこと」と記入. 少しでも頭をよぎった方針を回収するため, ここに方針を書いていきます.
まず言いたいことは非有界性, あわよくば単調性. これは$n$の式と$n+1$の式を比較して言えました. 狭義単調性まで言えたのでちょっと嬉しくなりました. そうしたら, イメージとして, $k$次のモニックな式に$n$を代入したものが, いくら大きくても分解できるというところから, さすがに$1$次式$k$個に分解されてほしくなります. これを数式にすると, $P$が$x+t$で割り切れないとき, あまりを考えるとちゃんと十分先で$P(n)$は$n+t$で割り切れなくなるので, 細かいところを議論したらなんとそのまま解けてしまいました...!?. かかった時間は45分ほど. あまりにスムーズに行きすぎて, にわかに信じられませんでした.
P3が解きやすい問題だったとはいえ, 全完より嬉しいことはないです. 金にも大きく近づいたので, ずっと浮かれていました.
Day2
Day1がNGAなので, Day2はACG, ACN, CAG, CANのどれかです.
IMOでは, 14, 25, 36, 123, および456に分野の重複はありません. 近年ではほぼ間違いなく1245にも重複がないようになっています.
全完をするためには, CAN, せめてACNを引く必要がありました. ACGは下手したら1完の可能性もあるため最悪です.
コンテスト会場の机にはDay1にはなかったバナナが置いてありました.
そして, 試験開始.
](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F3sDKV0ezeBHBIWPgR3JV.jpg?alt=media) Day2
Day2
分野はACG, 最悪です. こんなところで$\dfrac14$を引いてしまいました. しかし, 分野で落ち込んでいてはどうしようもないので解いていきます.
P4, Aでしかも不等式です. $3034$は$2023$の大体$1.5$倍なので, 差分$1$が$2$連続しないという終わり方だということが見た瞬間見えました. そうすれば考えるべきは差分$1$となるときの$x_{n+1}$の条件です. すると一意に決まったので, 差分$1$が$2$連続するとしたときの矛盾まで言えました. 15分経過. 深呼吸.
P5, 「絶対いける」と鼓舞します. この問題でも「したいこと」「分かったこと」の紙を用意. 方針を片っ端から書いていきます.
まずは実験を始めます.
$n=1, 2, 3, 4$あたりで全探索すると$1, 2, 2, 3$となり, $\dfrac{n}2+O(1)$かなと考えます. しかし, 構成に余裕がありそうという直感からもう少し構成を頑張ってみると, $\log_2n+O(1)$の構成が見つかります. 頭の中で2022春P4を重ねます. そしてこれが解だと確信します.
とすれば残すは評価.
- 構成の形から, $1$段, $2$段, $4$段, $\cdots$と区切って, 各セクションで一つずつ通る?
→左左左右右右右右...みたいな構成で詰む - ランダムなpathを考えて期待値?
→期待値は収束してしまった - 各マスまでのpathで赤マスの通る個数としてありうる最大値をDP?
→なんかよさそうだけど, 数をいまいち扱いづらそう
なんとなく進捗はありそうなものの, 決定打は見つかりません. しばらく難航した後, IMO直前の最後のメモ「行き詰まったときこそ案外正解は近くにある」を思い出しました. 今までの方針を振り返ります. そして実際, 赤マスの個数のDPをして, 各段の総和を考えると, 各段のMaxを使って差分が評価できました!
競技数学人生で一番嬉しかった瞬間です. 残り時間は1時間半.
P6, Gです. 簡単だと自分に何回も言い聞かせます. 意味不明な角度の条件は絶対もっと本質的な何かに言い換えられるはずです. 今回は, $A_1$が$A_2BC$の. そこからさらにangle-chaseをすると, $B_2C_2B_1C_1$の共円などが言え, それら3円の根心$X$を考えると, $X$は問題の$3$円の根心にもなっていました!!. つまり, もう一つ「根心」を見つければ問題を解けます...が, 全然見つかりませんでした...
終った直後は少し悔しかったです.
結果は777772で金メダル, 個人順位は12位/618人. 6はものすごく難しく, もう一つの「根心」を見つけるのが本質で7点中5点相当だったそうです.
全完は叶いませんでしたが, これが今の自分のすべてです. 悔いはありません.
その後
こちらの話は財団通信のほうの体験記で話します. 本当に楽しく刺激的で充実した一週間でした.
最後に
今期あったことをまとめると, 現役がついに終わってしまったという感覚があり, 少し寂しいですね. 最初に出たコンテストの小3のときのキッズBEEから約9年間, あっという間だった気がします. その過程で色々な方にお世話になり, 数学の魅力を知り, そして今の自分がいます. 感謝してもしきれません. 本当にありがとうございました.
数オリを目指す後輩たちに向けて
嬉しいことに, どうやったら数学ができるようになるかといった質問をよくいただきます. 競技数学に限って言えば, 一番は楽しむこと, もう少し踏み込んだ話をすれば問題や概念の本質を追い求めることだと考えています. 競技数学は受験とは違って, スポーツにもある類の娯楽の側面も大きいです. 楽しめなくなったら距離を置きましょう. そして, 学校行事や部活や, ほかの楽しいことを全力で楽しみましょう. いつかまた競技数学をしたくなったら競技数学を思いっきり楽しみましょう!
中高の6年間において競技数学はほんのただ一つの側面にすぎないわけです. 僕は数オリに参加する一方で兼部をしつつ, 音楽祭と文化祭の実行委員を兼任したりと, 人一倍学校生活も楽しむよう意識してきました. 少し飛躍させて言えば, そういった生活をしたからといって, 数オリにおいて大きなディスアドバンテージとなるといったことはないと思っています.
もちろん, 競技数学において努力の方向性を間違えないことは大前提です. これは先ほど少し話した, 「問題や概念の本質を追い求めること」というのが自分の出した結論です. この問題は結局どこを思いつくのが難しいのか, 何が本質か, どうやったら思いつくか, 面白さはどういうところか, あるいは, この概念はどういうモチベーションで作られたのか, 何に使えるのか, ...などなど(定義を正確につかむのはもちろんです). そしてそれをときにはまとめたりしてみる. それが一番の近道だと思います. しっかり触れたわけではないのであまり大きい声では言えないですが, 学問としての数学にも近いところはある気がします.
皆さん一人一人が悔いのない数オリ人生や学校生活を送れるよう陰ながら応援しています!
長く読みづらい箇所も多かったと思いましたが, ここまで読んでくださりありがとうございます!今後は受験もあり, 更新頻度は下がると思いますが, またどこかでお会いしましょう!
