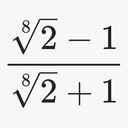q超幾何関数固有の連分数展開
通常の超幾何関数に対応するものは恐らくありません。
ロジャース=ラマヌジャン連分数
を系に含みます。
定義
定理
$|q|<1$
$\beginend{align}{
f(z) \acoloneqq \hygeo2\phi1{a,b}0{q,z} \\
\frac{f(qz)}{f(z)} &=
\frac{1-z}{1-(a+b)z +
\kfrac_{n=1}^\infty
\frac{abq^{n-1}z\qty(1-q^nz)}{1-(a+b)q^nz}} \\&=
\cfrac{1-z}
{1-(a+b)z+\cfrac{abz(1-qz)}
{1-(a+b)qz+\cfrac{abqz\qty(1-q^2z)}
{1-(a+b)q^2z+\ddots}}}
}$
$\beginend{align}{ f(z)-f(qz) &= \sum_{n=1}^\infty\frac{(a,b;q)_n}{(q;q)_n}(1-q^n)z^n = \sum_{n=1}^\infty\frac{(a,b;q)_n}{(q;q)_{n-1}}z^n \\&= \sum_{n=1}^\infty\frac{(a,b;q)_{n-1}}{(q;q)_{n-1}}\qty[1-(a+b)q^{n-1}+abq^{2n-2}]z^n \\&= z{\qty[f(z)-(a+b)f(qz)+abf{\qty(q^2z)}]} \\ (1-z)f(z) &= [1-(a+b)z]f(qz)+abzf{\qty(q^2z)} \quad\cdots(1) \\ (1-z)\frac{f(z)}{f(qz)} &= 1-(a+b)z+abz\frac{f{\qty(q^2z)}}{f(qz)} \\ \frac{f(z)}{f(qz)} &= \frac{1-(a+b)z+abz\frac{f{\qty(q^2z)}}{f(qz)}}{1-z} \\ \color{red}\frac{f(qz)}{f(z)} &= \frac{1-z}{1-(a+b)z+abz\color{red}\frac{f{\qty(q^2z)}}{f(qz)}} \\ \asupplement{-5.6em}{{\color{red}強調}部分の再帰的代入。} \\&= \frac{1-z}{1-(a+b)z + \kfrac_{n=1}^\infty\frac{abq^{n-1}z\qty(1-q^nz)}{1-(a+b)q^nz}} }$
これ自体はグラフの比較により成り立つことが確認できます。
実際$\displaystyle \lim_{n\to\infty} q^n=0, f(0)=1$であることを考慮すれば
$\displaystyle \lim_{N\to\infty} \frac{1-z}{1-(a+b)z +
\kfrac_{n=1}^N
\frac{abq^{n-1}z\qty(1-q^nz)}{1-(a+b)q^nz}} =
\frac{f(qz)}{f(z)}$
は厳密に正しいことが証明できます。
関数方程式$(1)$は$f(z) \coloneqq \hygeo2\phi1{a,b}c{q,z}$に一般化でき、
$(1-z)f(z) = \qty[1+\dfrac cq-(a+b)z]f(qz)+\qty(abz-\dfrac cq)f{\qty(q^2z)}$
となり$c=0$で$(1)$に一致します。
グラフの比較によると、関数方程式は成り立つにも関わらず、
それに基づいた連分数は$c\neq0$で$\dfrac{f(qz)}{f(z)}$と一致しません。
また、この場合上記の厳密な証明も使えません。
$\beginend{align}{ f(z) \acoloneqq \hygeo0\phi1{}0{q,z} = \sum_{n=0}^\infty \frac{q^{n(n-1)}z^n}{(q;q)_n} \\ \frac{f(qz)}{f(z)} &= \frac{1}{1 + \kfrac_{n=0}^\infty \frac{q^nz}1} \\&= \cfrac1 {1+\cfrac z {1+\cfrac{qz} {1+\cfrac{q^2z} {1+\small\ddots}}}} }$
$\displaystyle f(z)= \lim_{a\to\infty}\hygeo2\phi1{a,a}0{q,a^{-2}z}$