準同型定理を図いっぱいで理解しよう！（前編）

どうも

　こんにちは　ごててんという者です　いつか書こうと思っていた記事にようやく向き合うことにしました（※2年くらい逃げてました）

　この記事シリーズ（全2回）では、群論の重要な定理「準同型定理」を説明します。結構しっかり書いた記事ですので、そんなに気軽に読めない記事かもしれません！
　前編（この記事です）では「剰余群」について説明します。準同型定理を理解するために、ここの説明は欠かせませんので、文字数をしっかり割いて説明します。

　後編は→ https://mathlog.info/articles/nhIelluNjYOdlkMO5HTx

まずは復習

　早速 準同型定理を紹介...... といきたいところですが、それは後編の記事に任せて、復習からです。

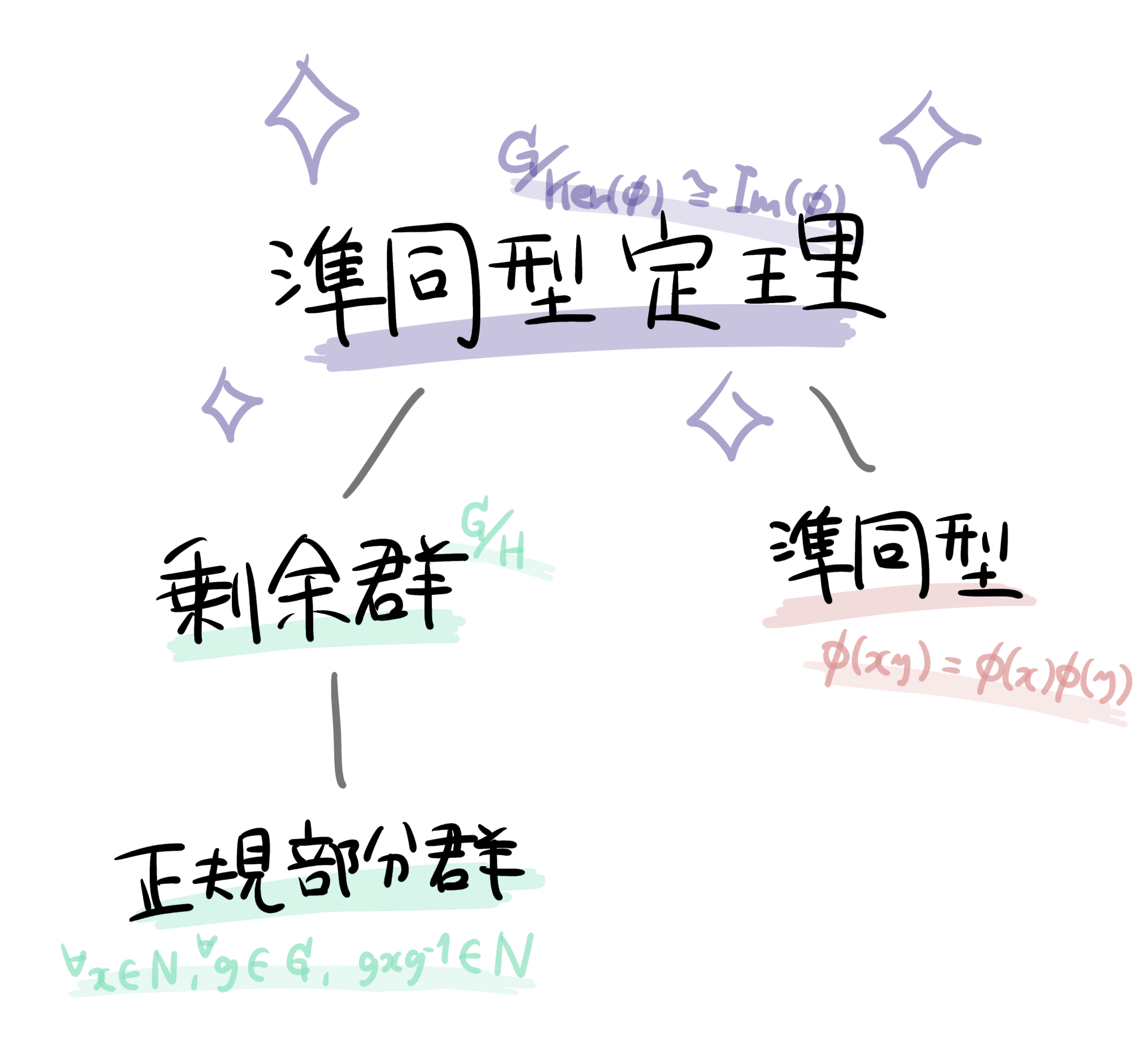
　準同型定理の説明の前に、次の3つを説明しなければなりません。

・正規部分群
・剰余群
・準同型写像

　この3つをダイジェスト的に解説します。（この記事で説明するのは、剰余群と正規部分群についてです。）というか、準同型定理を理解するにはここが一番大事です。準同型定理を受容できるほどの用語理解度を涵養していきましょう。

ネタバレ画像

剰余群とは？

　まずは「剰余群」の説明をします。線形代数を学んでいる場合には「商空間」を思い出していただけるといいかもしれません。

　剰余群というのは、「群を部分群で割って作った新しい群」です。

　次の問題を見てみてください。

　数学に慣れ親しんだ皆さんなら「$0$」と即答できると思います。どうして、単純に $2+3=5$で、それを$5$で割ったあまりが$0$だから$0$、としていいか。それは剰余群の立場から言えば$5\mathbb{Z}$が$\mathbb{Z}$の正規部分群だからと説明できます。

$\mathrm{mod}5$で考えることは、$5$の倍数の余りを考えているとも考えられますが、これは $5\mathbb{Z}$の差を無視するということです。そして剰余群というのは、部分群の差を無視するということです。

みんな大好き $\mathbb{Z}/n\mathbb{Z}$

　群論で屈指の使いやすさを誇る$\mathbb{Z}/n\mathbb{Z}$について考えてみます。

　$\mathbb{Z}/n\mathbb{Z}$というのは、上で言う「$n\mathbb{Z}$の差を無視する群」になります。ここでは具体的に$n=5$として「$\mathbb{Z}/5\mathbb{Z}$はどうやって作るのか」を説明します。

　$\mathbb{Z}/5\mathbb{Z}$の "中身" は次の画像のようになっています。

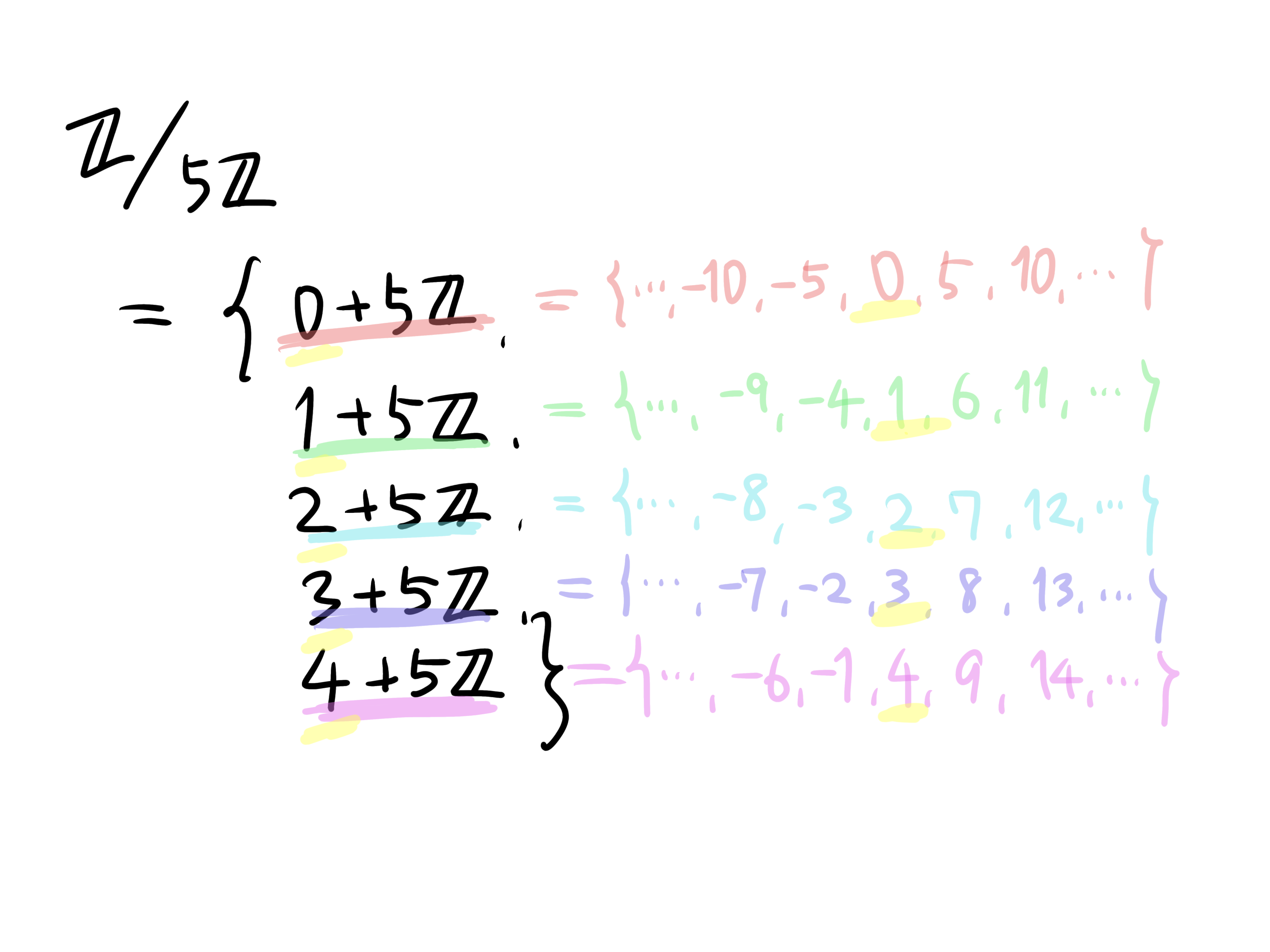図で描くのラクなので多用させてください......

　感覚的にわかりやすい記号なので説明はいらないかと思いますが、$m+n\mathbb{Z}=\{m+nx|x\in \mathbb{Z}\}$としています。

演算を定めよう！

　次に、$\mathbb{Z}/5\mathbb{Z}$の演算を定めます。ここからは詰みポイントです！注意してください！

　演算の定め方ですが、アイデア自体は簡単です。
　ただ、見やすくするために記法を導入します。$\overline{m}=m+5\mathbb{Z}$とします。

（この記法なら、$\mathbb{Z}/5\mathbb{Z}=\{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4}\}$と書き直すことができます。ただ何を法としているかが明示されない記法なのでこの記事では出し渋っています。）

　そうですね、この記号のもと、演算の定義をするとすれば次のような形になるのではないでしょうか。

・$\overline{a}+\overline{b}=\overline{a+b}$

　これで演算の定義は万全ですね！！！！！！！！！！

　...

　...

　...

　...

　すみません、 well-defined性を確かめていないようなのですが

　(>_<)

　
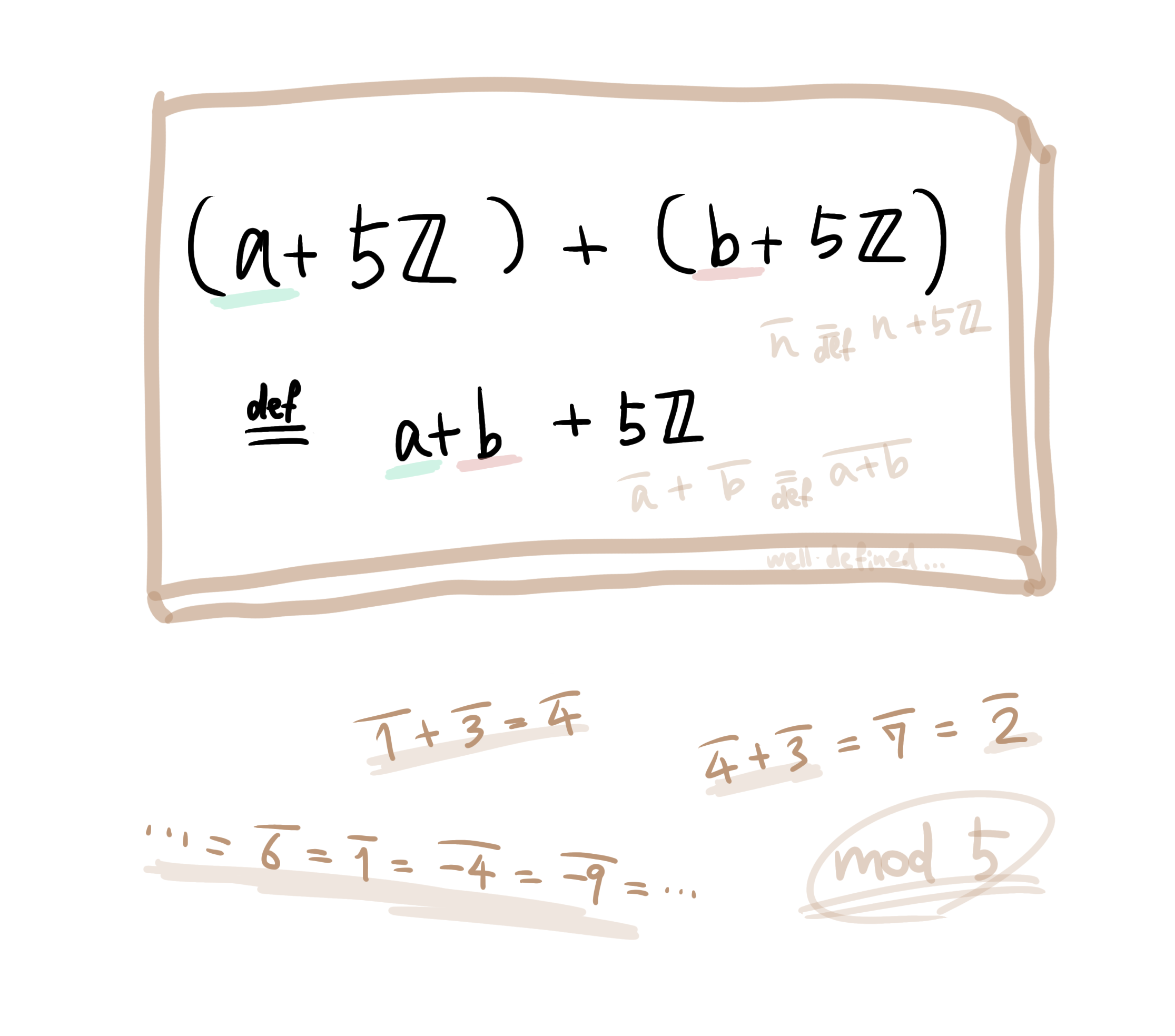アイキャッチ

ああ well-defined

　はい、では数学の有名詰みポイント well-defined について説明します。さっきの演算の定め方では何を確かめていなかったのか。それは置いておいて、一旦 well-defined について書きます。

　well-defined は、ちゃんと定義されている みたいな意味ではあるのですが、これは well-defined でない例 を見るのがいいです。その例を見てみましょう。

　写像$f:\mathbb{Q}\to \mathbb{Z}$を次のように定めます。有理数$q$を取ってきます。これを整数$a,b(b\ne 0)$を用いて$q=a/b$と書き、$f(q)=a+b$とします！！！

　いや、だめだろ！！！！！！！！

　$f(1/2)=1+2=3$ なのに $f(1/2)=f(2/4)=2+4=6$ とも取れてしまいます。これはダメです。より正確には、「$f$は写像になってない」です。こういう感じで、「見方によって結果が変わってしまう」状況はダメです。逆に、「見方によって結果が変わったりしない」のが well-defined です。

もとに戻って確認

　では$\mathbb{Z}/5\mathbb{Z}$の演算に戻ります。$\overline{a}+\overline{b}=\overline{a+b}$ としたのが引っ掛かりポイントでした。well-defined の解説を思い出しながら見てください。

　たとえば$\overline{2}$は、$\overline{7}$と書くこともできます。（この、書き方が複数あるという部分が問題の火種となります。）もしかしたら$\overline{2}+\overline{3}$の結果と$\overline{7}+\overline{3}$の結果が違うかもしれません。

　上の例は$1/2$を$2/4$と別の書き方をしたことで違う結果になりました。こういったことが起きない、これはちゃんとした定義ですよ！（←これが well-defined のことだと思って良いです）というのを示さなければなりません。

犯罪行為

何を示せばいい？

　$\overline{a},\overline{b}\in \mathbb{Z}/5\mathbb{Z}$の別の書き方を想定すればよいです。
　$\overline{a}=\overline{a^{\prime }},\overline{b}=\overline{b^{\prime }}$（$a,b,a^{\prime },b^{\prime }\in \mathbb{Z}$）とするとき、$\overline{a+b}=\overline{a^{\prime }+b^{\prime }}$となればよいです。

　まあこれは簡単です。$\overline{a}=\overline{a^{\prime }},$ $\overline{b}=\overline{b^{\prime }}$より$a^{\prime }=a+5m,$ $b^{\prime }=b+5l$と書けます。($m,l\in \mathbb{Z}$) ここから$\overline{a^{\prime }+b^{\prime }}=\overline{a+b+5(m+l)}=\overline{a+b}$がわかります。（$\overline{m}=m+5\mathbb{Z}$だったことを思い出せば明らかです）
　これでwell-definedであることが示されました！簡単ですね。

$\mathbb{Z}/5\mathbb{Z}$のまとめ

　$\mathbb{Z}/5\mathbb{Z}$は $0+5\mathbb{Z},$$0+5\mathbb{Z},$$1+5\mathbb{Z},$$2+5\mathbb{Z},$$3+5\mathbb{Z},$$4+5\mathbb{Z}$ の$5$つの元による集合で、そこに演算$\overline{a}+\overline{b}=\overline{a+b}$を定めました。それが well-defined であることも示しました。

じゃあ剰余群って

　剰余群は、上の$\mathbb{Z}$と$5\mathbb{Z}$から$\mathbb{Z}/5\mathbb{Z}$を作った流れを、もっと一般の群で行ってできたものです。
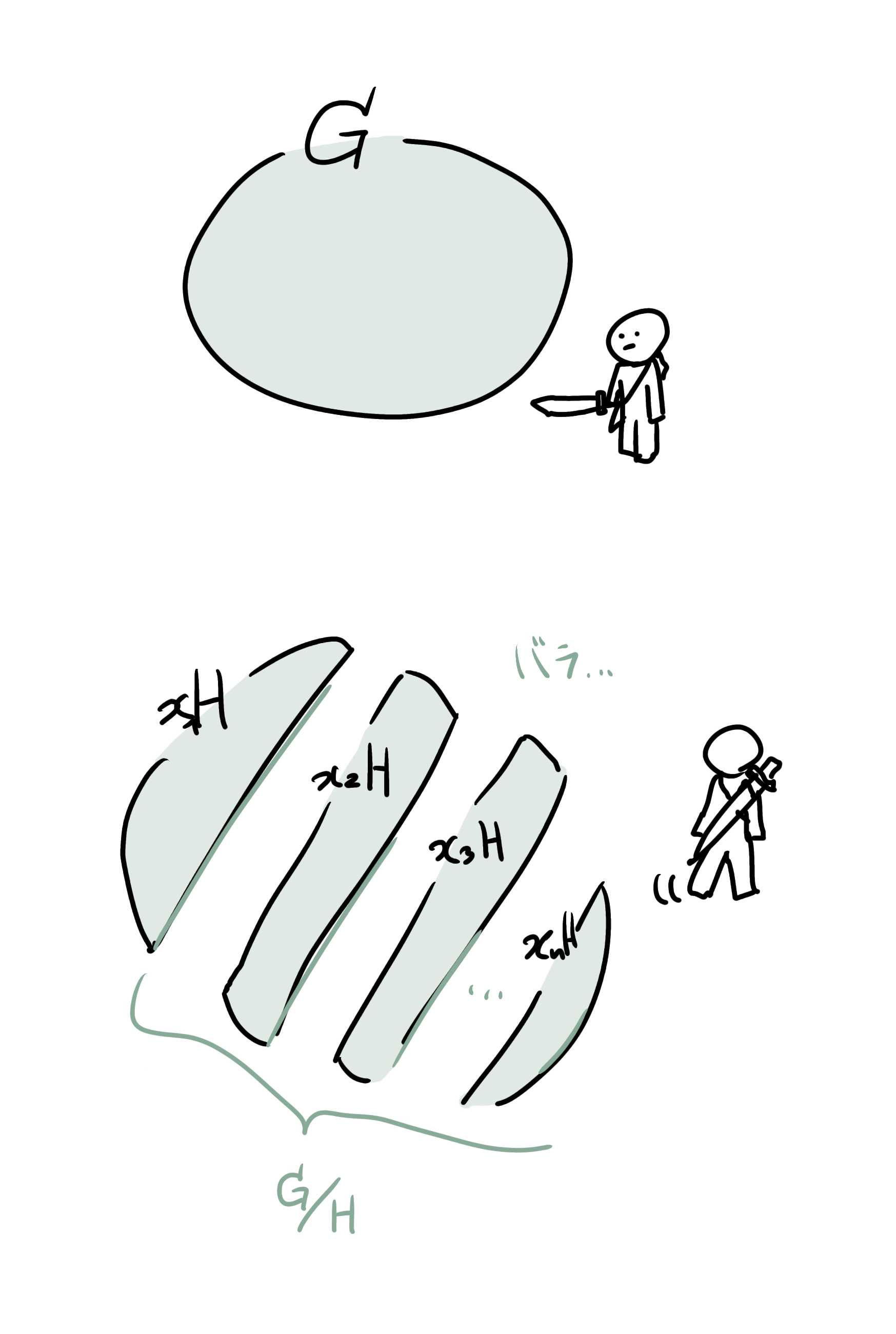
　群$G$とその部分群$H$から群$G/H$を作ります。

　$G/H$は、具体的に構成できます。それは、次のような構成です。

　$G/H=\{$$xH$$|$$x\in G$$\}$.（$xH=\{$$xh$$|$$h\in H$$\}$）

　これは群の演算を積の形で書いていた場合で、演算の記号が$+$だった場合は次のように書けます。

　$G/H=\{$$x+H$$|$$x\in G$$\}$.（$x+H=\{$$x+h$$|$$h\in H$$\}$）

　こちらで$G=\mathbb{Z},H=5\mathbb{Z}$としたものが$\mathbb{Z}/5\mathbb{Z}$に他なりません。

　$xH$とか$x+H$は、部分群から$x$ずらしたもののことです。例えば$2+5\mathbb{Z}$のことで、これは$5$の倍数全体という部分群から$2$ずらしたものです。

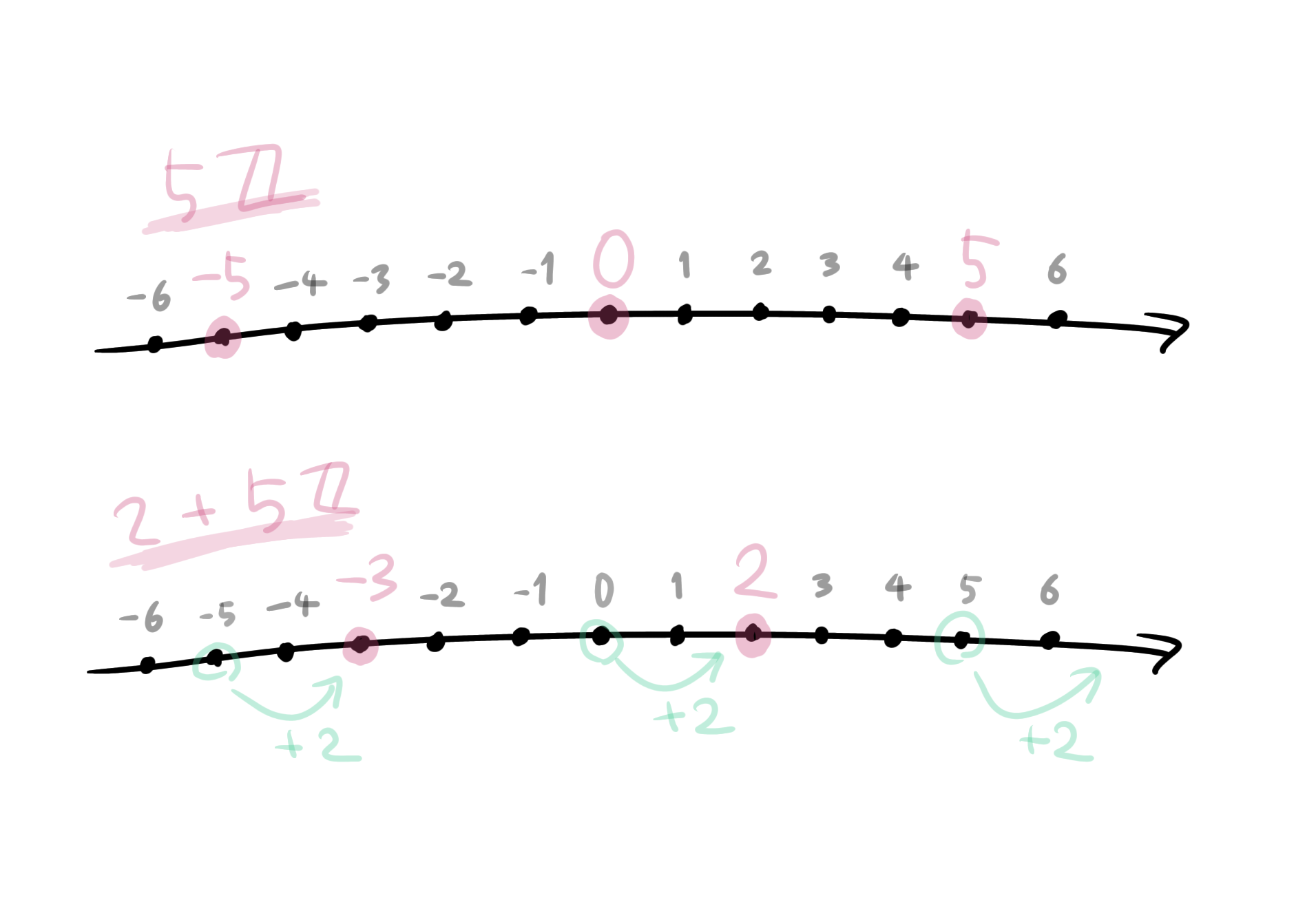全部の元を+2でずらす

　もう一度定義を貼っておきます。$G/H=\{$$xH$$|$$x\in G$$\}$.（$xH=\{$$xh$$|$$h\in H$$\}$）

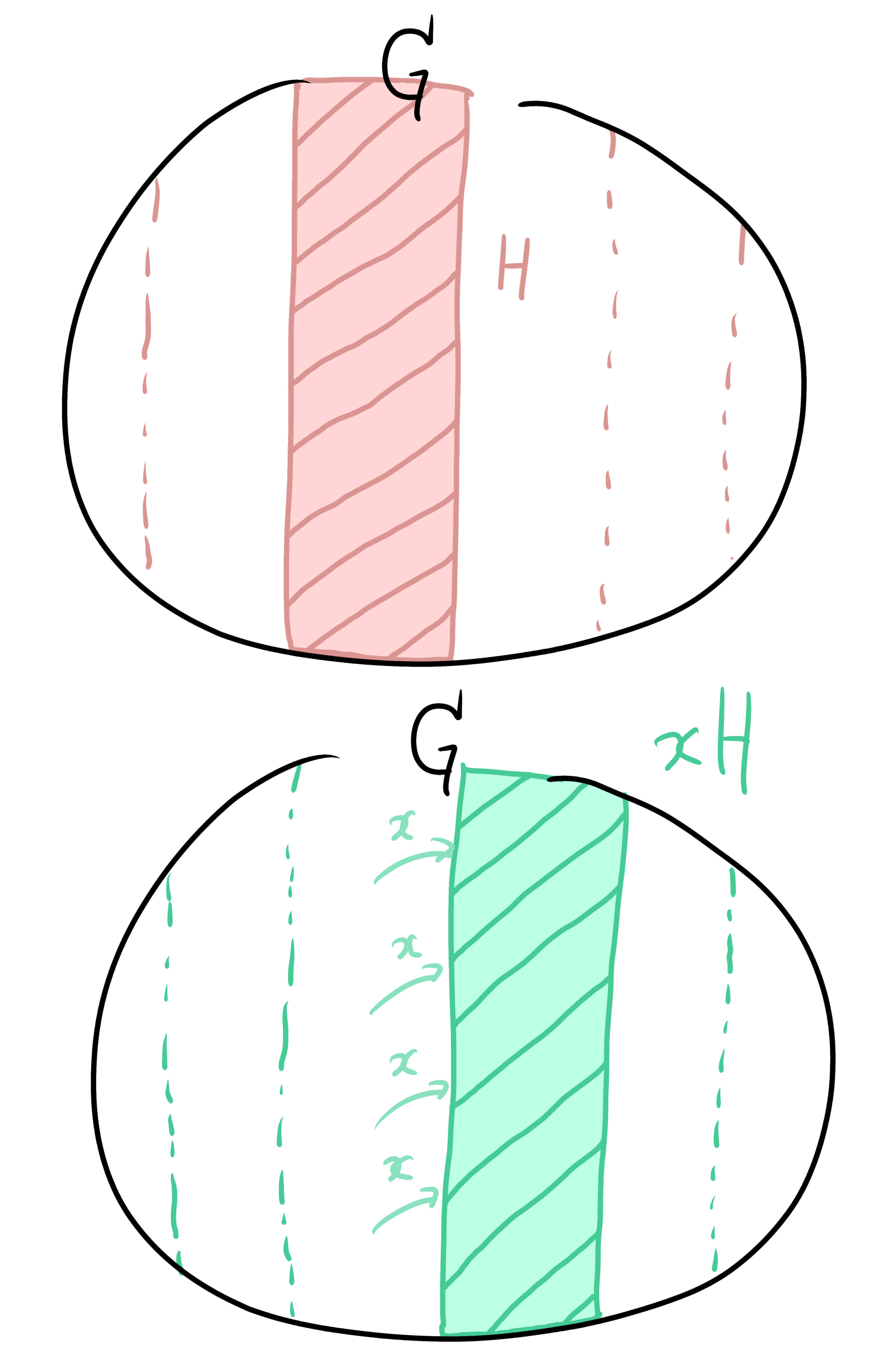部分群をxだけずらす

じゃあ演算は？

　さてさて、$\mathbb{Z}/5\mathbb{Z}$の演算は結構フツーに定めていましたね。$G/H$もフツーに定めます。$G/H$の元$xH$と$yH$について二項演算を定めよう！という話です。
　次のような感じです。

　$(xH)(yH)=xyH$.

　カンタン～～～ 至極単純です。これで演算もバッチリですね！！！！！！！！！！

　...

　...

　...

　...

　すみません、 well-defined性を確かめていないようなのですが

　(>_<)

アイキャッチ

ああ well-defined どうして

　前回は well-defined のチェックを$\mathbb{Z}/5\mathbb{Z}$の演算に対して行いました。これはしょっぴかれませんでした。しかし今回は、well-defined とならない例が実際にあります。有罪判決です。

　$G$を$3$次対称群$S_3$として、$H$をその部分群$H=\{1,(12)\}$とします。何も変えない置換$1$と、$1$と$2$を入れ替える互換$(12)$です。これは部分群です。そして、このとき$G/H$に上で書いた演算を考えると、well-defined となりません！

　えっと、「これだとうまくいかないらしい！」くらいの認識でいいと思います。これがどうして well-defined でないかをきちんと計算で追うのがこの時点での群論の理解につながるかというと、そうでもないと思います。群論の基礎がちゃんと分かってきた気がしたくらいのときに自分で計算してみるくらいでいいと思います。

　一応ちゃんと計算を貼っておきますが、文字で打つのが面倒になったので画像一枚で済ましちゃいますね、、、読まなくていいです

読まなくていいです

　ではなぜ$\mathbb{Z}/5\mathbb{Z}$ではうまく行ったのでしょうか。これは$5\mathbb{Z}$が$\mathbb{Z}$の正規部分群であるからです。

正規部分群

　正規部分群の説明をしたいのですが、正直なところ 準同型定理を理解するという目的なら正規部分群をちゃんとわかる必要は無いと思います。なので、この記事シリーズを読み切るくらいのためなら雑な理解で大丈夫です。

　群$G$の部分群$N$が正規部分群であるとは、任意の$G$の元$g$と任意の$N$の元$x$に対して$gx{g}^{-1}\in N$が成立することです。よくわかりませんね。正直ここではよくわからなくていいです。ではなぜ説明したかですが、剰余群の説明に必要だからです。

剰余群における正規部分群って

　$G/H=\{$$xH$$|$$x\in G$$\}$.（$xH=\{$$xh$$|$$h\in H$$\}$）

　上のように定義された$G/H$に演算を入れたいのに、well-defined でなくなってしまう場合があるのでした。ここで正規部分群が活躍します！

　先程は脆くも崩れ去りました演算規則、$(xH)(yH)=xyH$ は、$H$が正規部分群のとき well-defined となります！

名前だけでも覚えて帰ってください

　なぜ well-defined になるかですが、一応証明を打つのが面倒だったので画像で載せておきます。ただ、別に納得感があるとかそういうものでもないので、そんなにちゃんと追わなくていいと思います。理解度が上がってきた頃に自力で証明すればいいやくらいに思っておいて大丈夫だと思います。

（以下、$N$が正規部分群なら演算$(xN)(yN)=xyN$がwell-definedになる証明）
（補足を書きまくったらかえって見づらくなった）

正直ぜんぶ手書きで記事を書きたい

ようやく

　はい。このようにして$G/H$に演算が定まるとき、その演算で$G/H$は群になります。（証明してみてください！）この群を剰余群と呼びます。

可換の場合

　正規部分群の定義を振り返ってみましょう。群$G$の部分群$N$が正規部分群であるとは、任意の$G$の元$g$と任意の$N$の元$x$に対して$gx{g}^{-1}\in N$が成立することでした。
　$G$が可換の場合は、$gx{g}^{-1}=xg{g}^{-1}=x\in N$より、部分群はもれなくすべて正規部分群となります。

一般論のまとめ

　ここまで述べた内容を画像一枚にまとめました。ウオオオオ

この画像一枚でいい

最後に具体例を

　この記事にはまだ足りないものがあります。剰余群の具体例です。$\mathbb{Z}/5\mathbb{Z}$以外のものも紹介します。

$\mathbb{R}/\mathbb{Z}$

　$\mathbb{R}/\mathbb{Z}$はよく出てくる例ですね。具体的な元は$x+\mathbb{Z}$の形をしていて、これは整数全体の集合を$x$だけずらしたものになります。

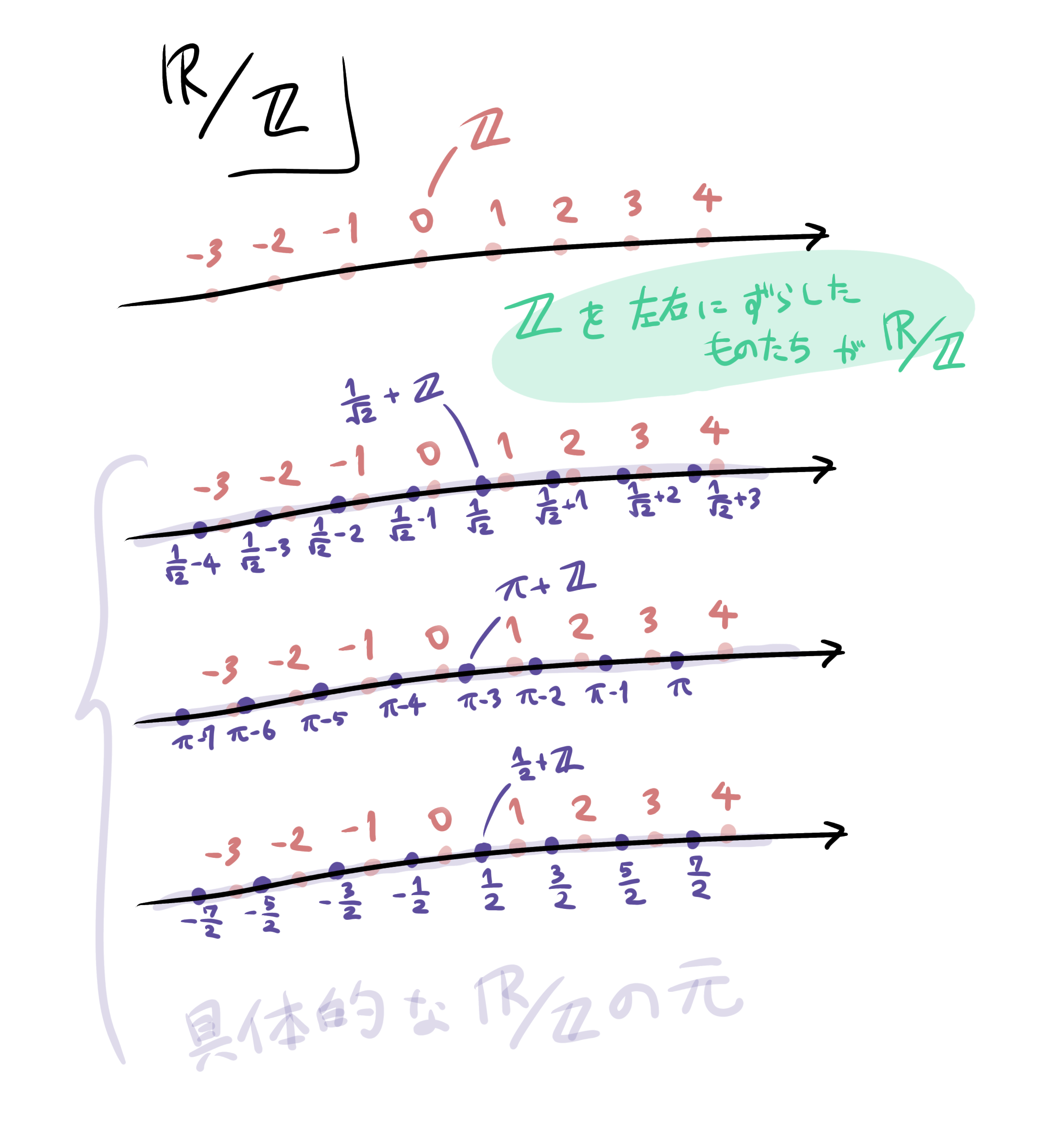具体例その順番で書くことある？

　これは周期$1$の関数を$\mathbb{R}/\mathbb{Z}$上の関数とみなすとかで使ってるのを見たことがあります。（それを使って$S^1$のド・ラームコホモロジーを求めるpdfがあったと思ったんですが見つかりませんでした......）

　またこれは、整数の違いを無視している群です。言うならば$\mathrm{mod}1$　ということですね。

　他に非可換な例とかも出したいのですが、どうしても複雑になってしまうのでやめておきます。

お疲れ様でした

　これで前編は終了です。長かったですね～～～
　「$G/H$は$H$が正規部分群なら演算が$(xH)(yH)=xyH$で定まり剰余群となる。」というのを叩き込んでください！
　ここまで読んでいただきありがとうございました～～～～～

　後編は→ https://mathlog.info/articles/nhIelluNjYOdlkMO5HTx