準同型定理を図いっぱいで理解しよう！（後編）

どうも

　こんにちは　ごててんという者です　いつか書こうと思っていた記事をようやく書き終えました（※2年くらい逃げてました）

　この記事シリーズ（全2回）では、群論の重要な定理「準同型定理」を説明します。結構しっかり書いた記事ですので、そんなに気軽に読めない記事かもしれません！
　後編（この記事です）では「準同型」「準同型定理」について説明します。いよいよ本番です。

　前編は→ https://mathlog.info/articles/sTacgC5iT24V4aWjLhiu

準同型について

　準同型の説明です。無茶苦茶雑なことを書くと、群と群の間のいいかんじの写像のことです。定義を見ましょう。

　線形代数や微積分をやっていて、たびたび「代数的に」いい感じの写像に出会ってきたと思います。これはそれらを包括しています。

　例をいっぱい出します！

　結構ビッグネーム（？）が出てきますね。準同型はそれくらい広い概念です。一応触れておきますが、「線形写像」も準同型の例です。

準同型の基礎知識

　準同型の、すぐわかる性質を述べておきます。

　$\phi:G_1\rightarrow G_2$を準同型とすると、$\phi$は単位元は送っても単位元です。$\phi$は逆元を送っても逆元です。ちゃんとした主張は画像で済ましちゃいますね。
演算の構造をある程度保ってくれる

同型

　さて、群論でキモとなる概念である「同型」について説明します。

　「同型」は...... まあ群と群の間に同型があったらその2つの群は同じとみなします。そのくらいの認識でいいと思います。より正確に言えば、「$G_1 \cong G_2$としたとき、$G_1$が◯◯なら$G_2$も◯◯になる」というような◯◯が群論で扱われる性質...... という感じです。例えば◯◯には「巡回群」とか「可換群」とかが入ります。

　同型という概念自体は重要ですが、別に話すことがあるかというと別に無い、という感じです。群論の範疇で 対象が「同じ」とはなにか を規定するのが同型の概念、という認識で問題ありません。

同型の例

　例ですが、準同型定理を説明する中で色々証明します。ですので、ここでは控えめに例を紹介しようと思います。

　このくらいにしておきましょう。

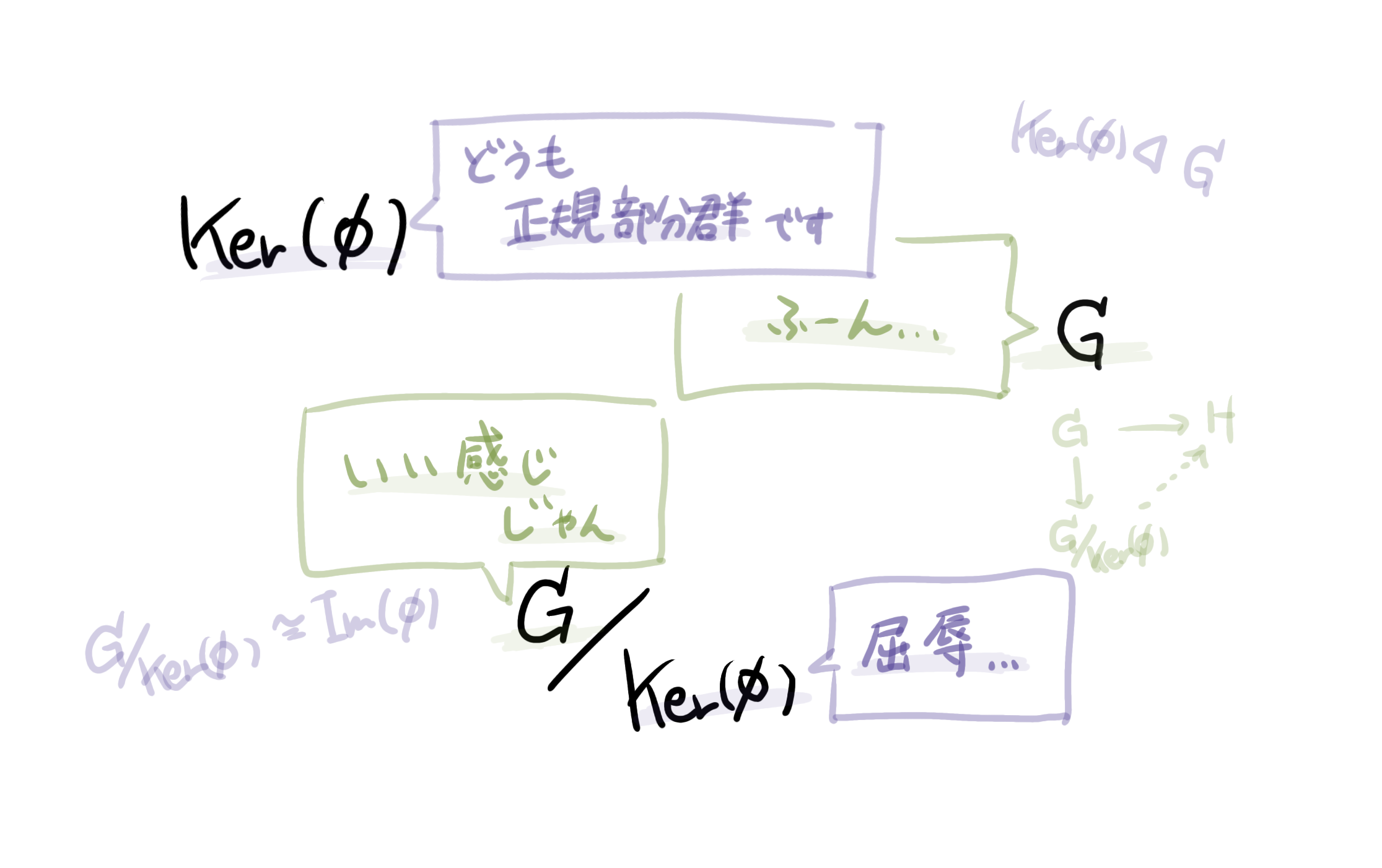
準同型の核（超重要）

　準同型定理を理解するために一番大事なのが$\mathrm{Ker}(\phi)$と書かれる、準同型の「核(Kernel)」です。これが...... 本当に大事です。 まずは定義をします。

　この命題は大事です。（証明は省略します。）
　前編を思い出してみてください。（読んでない人は別に大丈夫です。）「$G/H$は$H$が正規部分群なら演算が$(xH)(yH)=xyH$で定まり剰余群となる。」のでした。いま、$\mathrm{Ker}(\phi)$という、結構カノニカルな正規部分群が得られました。......これで剰余群を考えたら何か起きてくれそうですよね？ それが準同型定理に繋がります。

アイキャッチ

この記事の主定理

　さて、この記事のキーとなる定理が次になります。この定理は超大事だぞ！！！！！！！！！！！！！と言うためにここまで5,000文字打ったと言っても過言ではありません。

　これがたいへんに準同型定理を理解するための助けになります。
　この定理は「単射」と「$\mathrm{Ker}(\phi)=\{1\}$」を結びつけるものですが、これをもう少し深読みしてみましょう。
　物事というのは往々にしてグラデーションです。「数学が好き」というのも度合いがありますよね。「親しみやすい数学の雑学はちょっと楽しめる」から「数学者になる以外の人生が想像つかない」など、色々あります。さて、「単射」という言葉ですが、これは「極端」ですよね。

「単射」は極端な性質

　例えばですが、次のような3つの写像を考えてみましょう。

・$f:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ f(x)=\abs{x} $. 絶対値を取る写像
・$g:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ g(0)=0 $ or $ g(x)=x/\abs{x}$ $(x\ne0) $. 符号を得る写像
・$h:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ h(x)=1 $. すべて$1$に送る写像

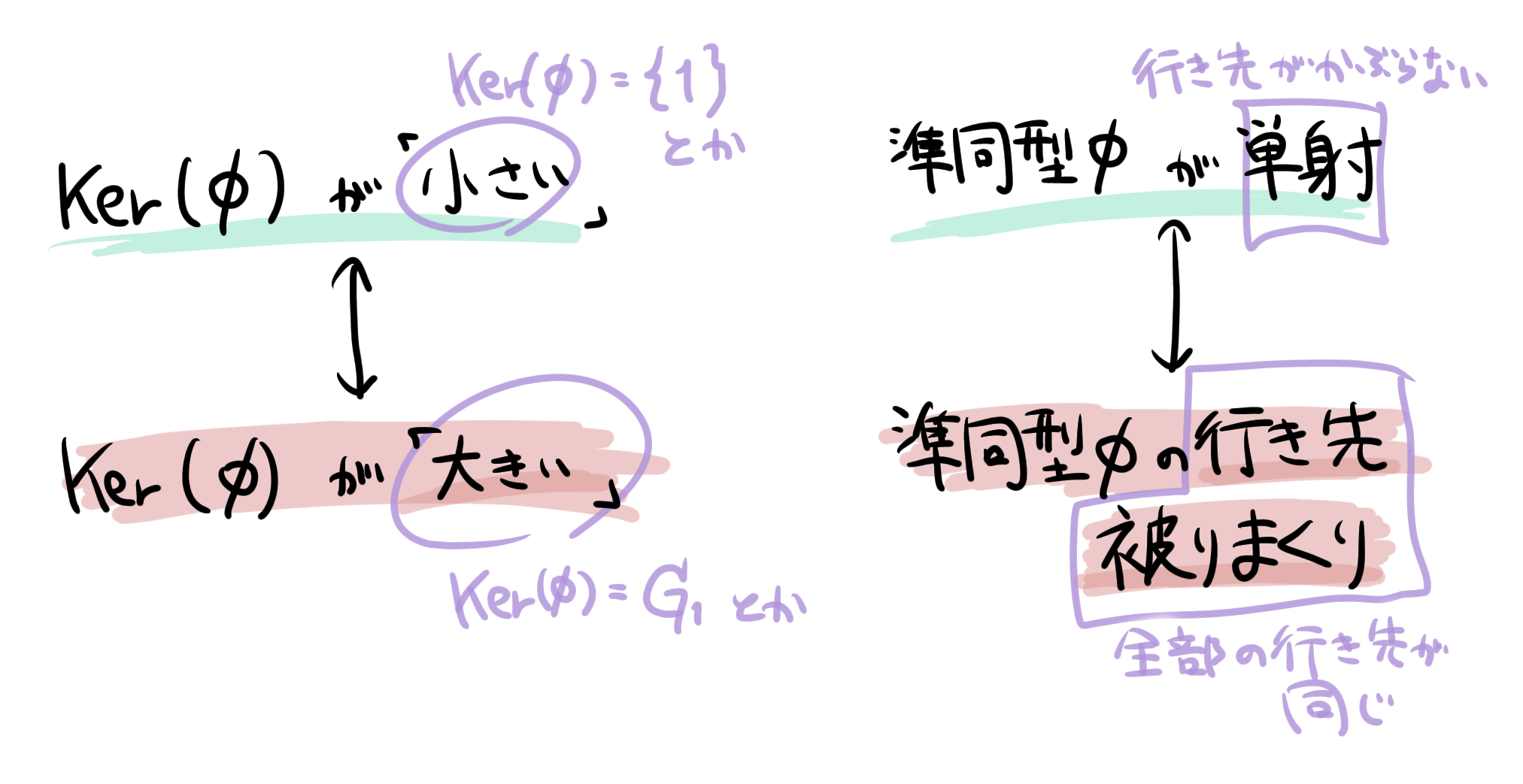
　これらはすべて単射ではありませんが、「単射っぽさ」を考えたら $f>g>h$ という気がしませんでしょうか。

　単射というのは、「行き先のかぶらなさ」が一番大きい場合のことです。そして、準同型における$\mathrm{Ker(\phi)}$というのは、「準同型写像の行き先がどれだけ被っているか」を表します。上の定理で言えば、「単射」という、いちばん行き先が被らない状況に「$\mathrm{Ker(\phi)}$が一元集合」という事実が対応しているということです。

核の小ささと単射っぽさが対応

像についても触れる

　$\mathrm{Im}(\phi)$も単射かどうかを表す側面があります。また次の3つの写像を見てみましょう。

・$f:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ f(x)=\abs{x} $. 絶対値を取る写像
・$g:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ g(0)=0 $ or $ g(x)=x/\abs{x}$ $(x\ne0) $. 符号を得る写像
・$h:\mathbb{Z}\rightarrow\mathbb{Z}$ $;$ $ h(x)=1 $. すべて$1$に送る写像

　上の方が「単射っぽい」ですが、「像が大きい」というのがありますね。

　「$\mathrm{Ker}(\phi)$が小さい」と「単射っぽい」、そして「$\mathrm{Im}(\phi)$が大きい」

　つまり「$\mathrm{Ker}(\phi)$が小さい」と「$\mathrm{Im}(\phi)$が大きい」
　これも理解の助けになるはずです。

　...

　...

　...

準同型定理

　さあ！！！ここまで長かったですね！！！ようやく本題です！！！！！！！

　アイキャッチをもう一度貼りますね。

またこのアイキャッチ

　ここに出てくる$G/\mathrm{Ker}(\phi)$が主役です。準同型$\phi:G_1 \rightarrow G_2$が与えられたとき、$\mathrm{Ker}(\phi)$という正規部分群が得られるのでそれで割ってみます。すると現れるものが$G/\mathrm{Ker}(\phi)$なのですが、これがなんと...... それでは準同型定理です。

　なんと...... 像と同型だったんですね！！！このイメージをゆっくり説明していきます。キーワードは、「準同型を無理やり全単射にして同型を作る」です。

そもそもどんな同型写像？

　上の主張では具体的な同型を与えていないのですが、実際には同型写像の構成方法まで与えられています。ですが、その構成方法の具体例を見てみましょう。そして、その構成方法を理解することが準同型定理の理解に繋がります。

絶対値を取る写像

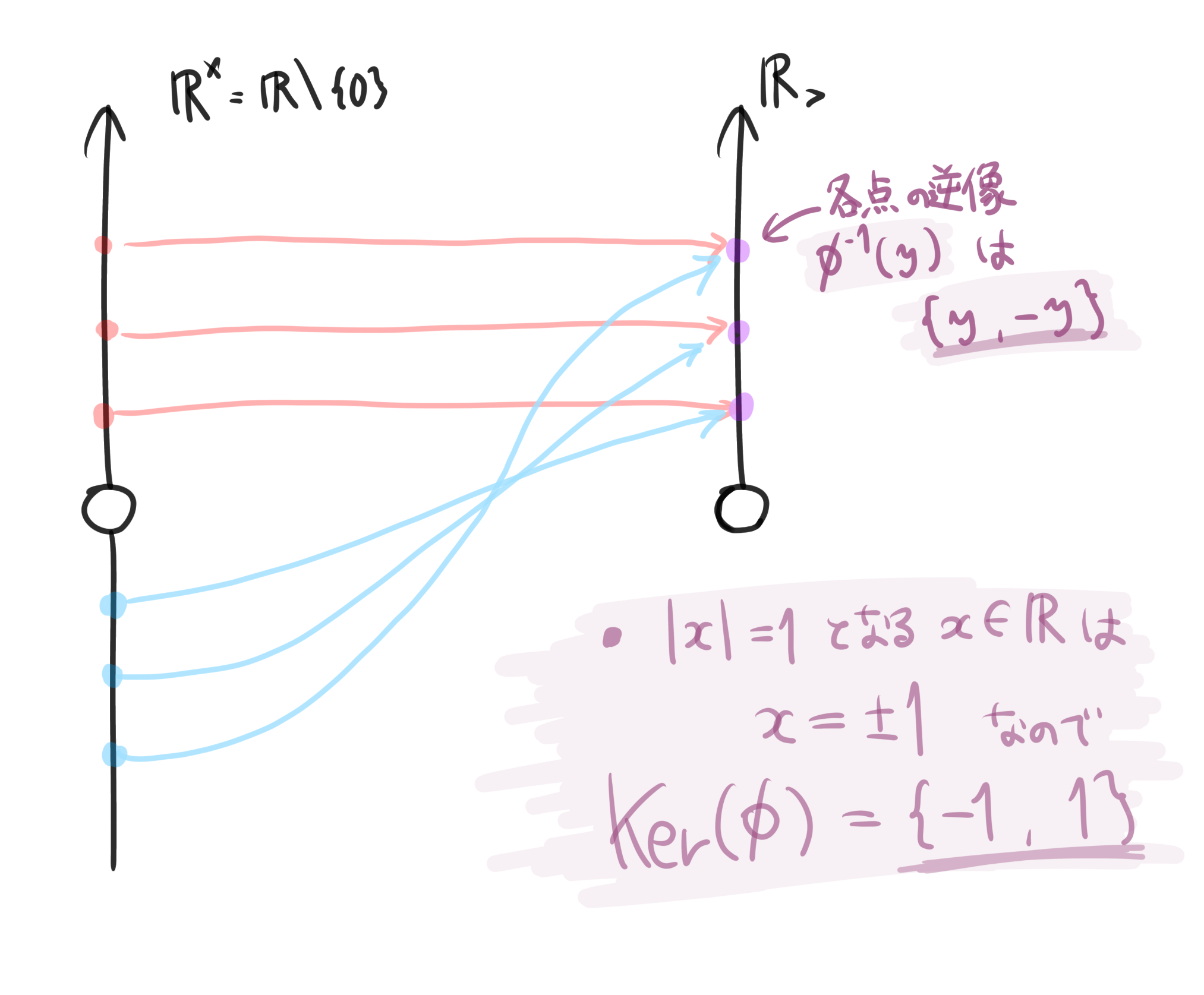
　$\mathbb{R}_>=\{r\in \mathbb{R} | r > 0 \}$とします。このとき、写像$\phi:\mathbb{R} \setminus \{0\} \rightarrow \mathbb{R}_>$を、絶対値を取る準同型 $x \mapsto \abs{x}$で定めます。
　この、特に単射でもない準同型から、全単射な同型写像を作るのが準同型定理です。それをやってみます。次の図を見てみてください。

2つの点が1つの点に対応

　とまあこんな感じの図が想像できると思います。さて、ここから全単射な写像を作りたいので、まずは単射にしてみましょう。さて単射にするためには、定義域を変えないといけません。どう変えれば良いでしょうか？ そうですね。正負を無視すれば良いです。

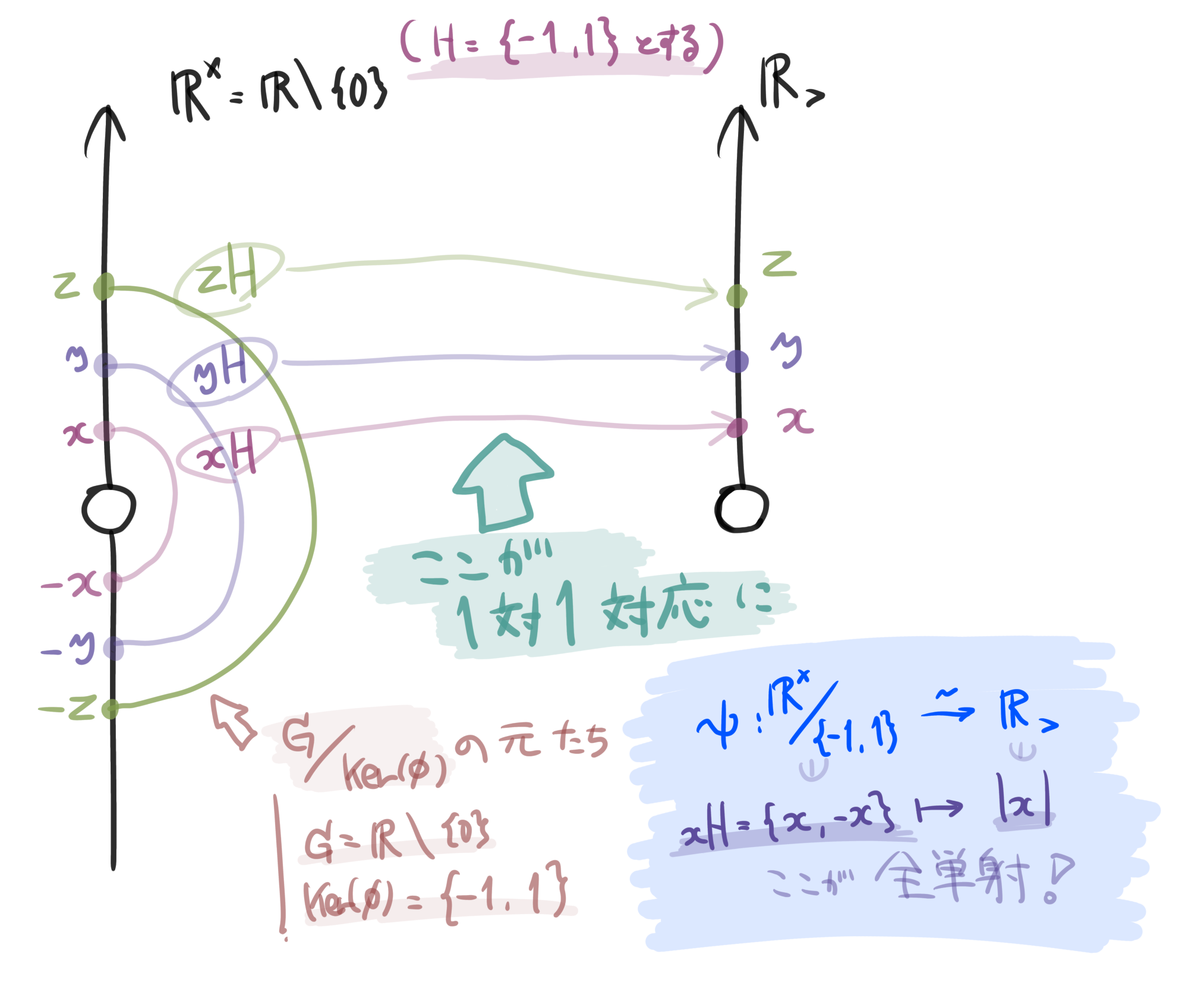
　さて、前編の記事でちらっと書いたことなのですが、$\mathbb{Z}/5\mathbb{Z}$というのは$5\mathbb{Z}$の差を無視してできたものでした。では正負を無視するにはどうするか。そうですね。部分群$\{1,-1\}$で剰余群を作ればいいです。そして$\{1,-1\}$は、この場合の$\mathrm{Ker}(\phi)$に他なりません！！！

情報を詰め込んだ図

　上の図で分かっていただけるかもしれませんが、これで全単射の完成です。どういう写像かなのですが、$x\mathrm{Ker}(\phi)$、つまり$x\{-1,1\}=\{-x,x\}$ から $\phi(x)$、つまり$\abs{x}$に対応させます。これが全単射になっている、ということです。
　ここから同型を書き下すと、$(\mathbb{R}\setminus \{0\}) / \{-1,1\} \cong\mathbb{R}_>$という感じです。（見た目キモ！！！）そして、$\phi$は全射でしたので、$\mathrm{Im}(\phi)=\mathbb{R}_>$です。これと$\mathrm{Ker}(\phi)=\{-1,1\}$を合わせると、上の準同型定理で見たような、$G/\mathrm{Ker}(\phi) \cong \mathrm{Im}(\phi)$という形にまとめることができます。

じゃあ抽象的に

　さてさて、準同型定理の同型を構成する対応を書いてみます。それは上でも赤字で強調した$x\mathrm{Ker}(\phi)$と$\phi(x)$の対応によります。これが1対1に対応しています。

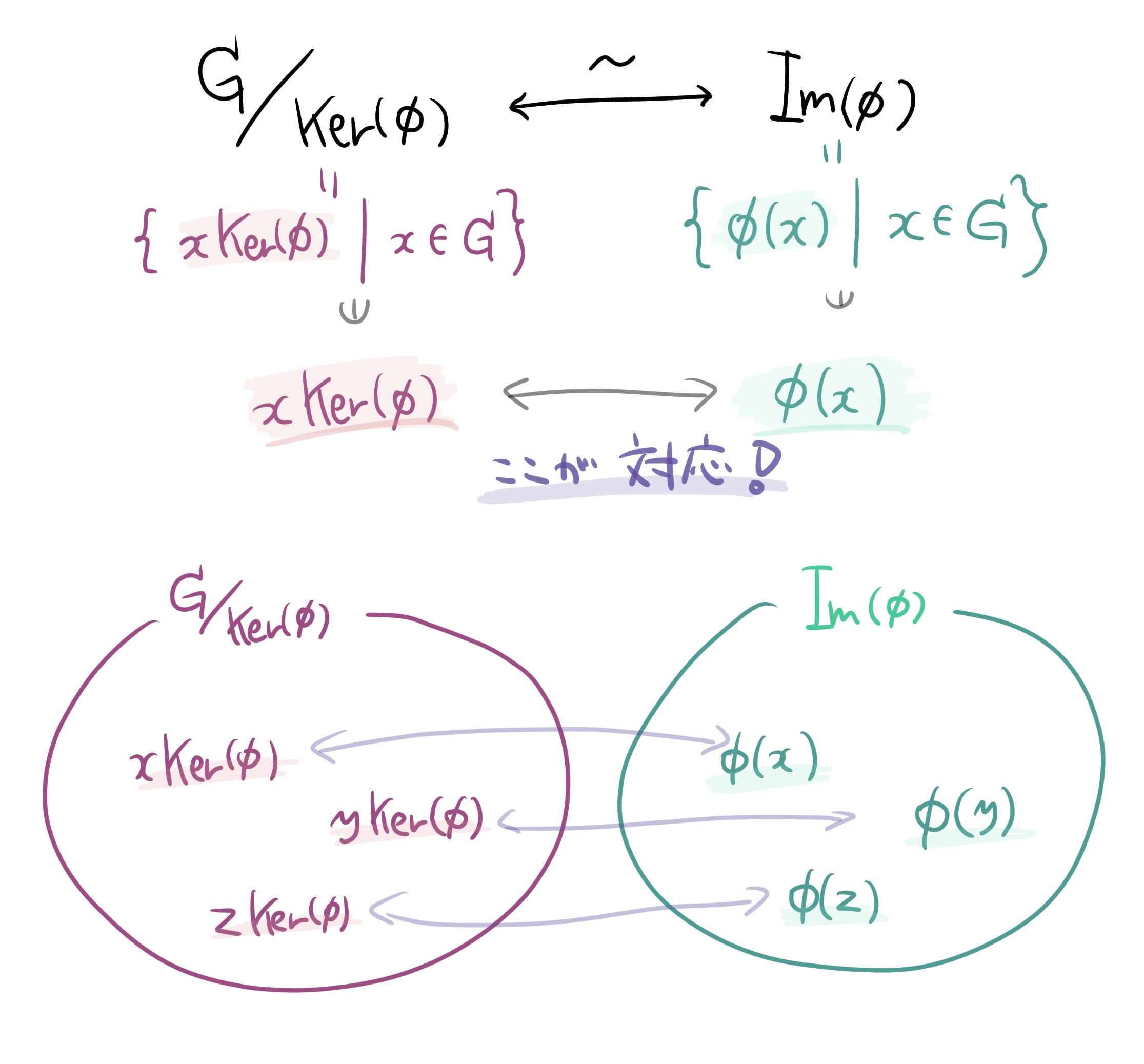この図が自分で描けるとよい？

　では、この対応の写像 $x\mathrm{Ker}(\phi) \mapsto \phi(x)$ で同型が定まることを示せば準同型定理を得られますね！

　...

　...

　...

　
　すみません、 well-defined性を確かめていないようなのですが

　
　(>_<)

ここでも well-defined

　前編でも説明しました well-defined が、またここでも問題となります。$x\mathrm{Ker}(\phi) \mapsto \phi(x)$ の対応のどこが良くないか。そうですね。$x\mathrm{Ker}(\phi)$は書き方が複数ある可能性があります。（$2+5\mathbb{Z}$は$2+5\mathbb{Z}=7+5\mathbb{Z}$のように複数通りの書き方がある話のことです。）

　
　さて、対応が well-defined, すなわち$x\mathrm{Ker}(\phi)$の書き方に依らず$\phi(x)$が定まることを示すのですが、$x\mathrm{Ker}(\phi) = y\mathrm{Ker}(\phi)$なら$\phi(x)=\phi(y)$であることがわかれば良いです。これは一瞬です。

　　
　$x\mathrm{Ker}(\phi) = y\mathrm{Ker}(\phi)$と仮定します。このとき$k \in \mathrm{Ker}(\phi)$があり$x=yk$と書けるので、$\phi(x)=\phi(yk)=\phi(y)\phi(k)=\phi(y)$がわかります.（$k \in \mathrm{Ker}(\phi)$から$\phi(k)=1$が分かります。）

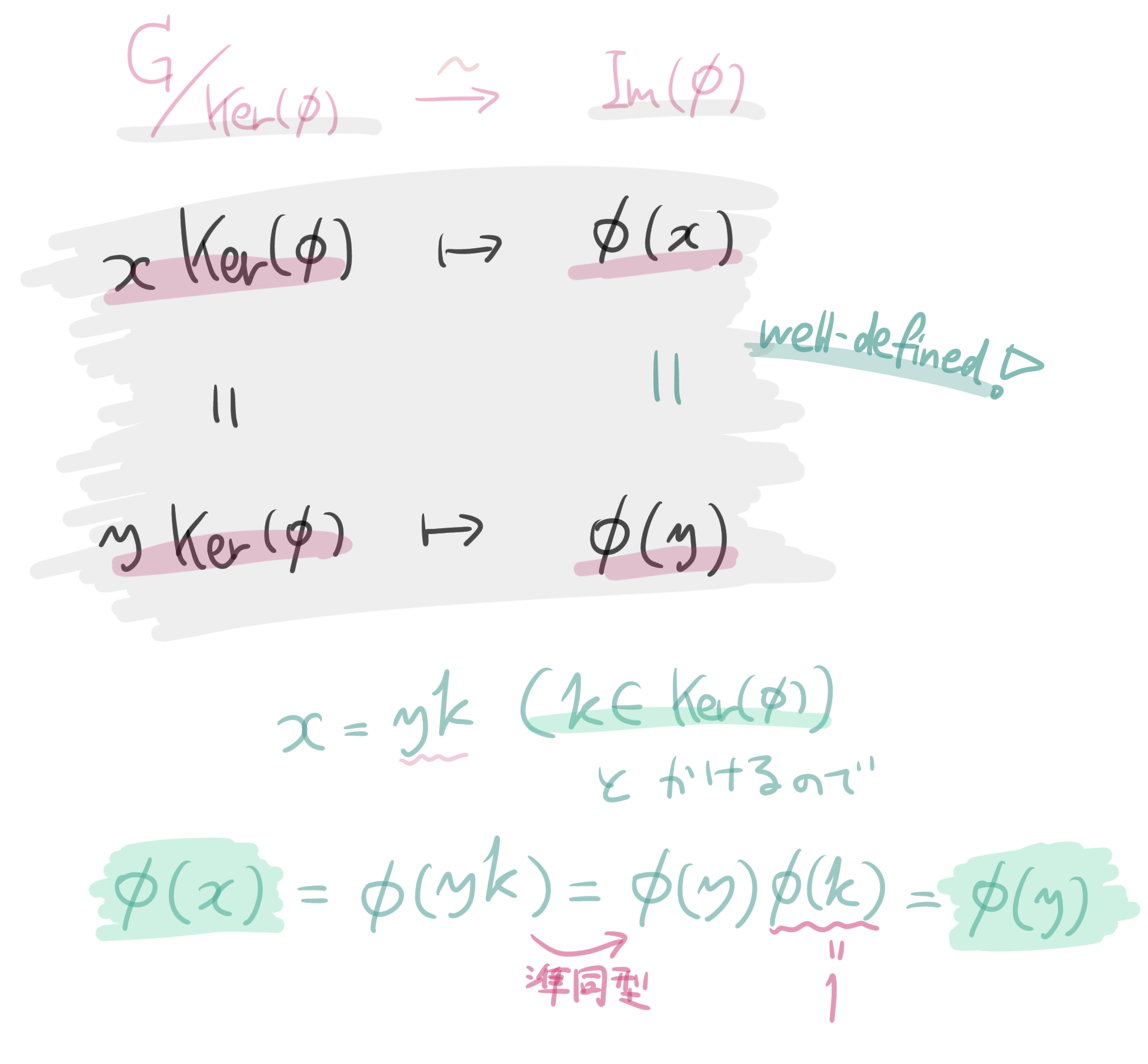well-defined

これが同型写像になることを示そう！

　さて、$x\mathrm{Ker}(\phi) \mapsto \phi(x)$が同型を与えていることを示しましょう。同型であることを示すステップをまとめます。

・準同型であることを示す

・全射であることを示す

・単射であることを示す

　実は同型写像であることを示すには、「準同型+全単射」であることを示せば良い（証明略）ので、これで良いです。

　イメージしやすいと思うので、以前ツイートした内容を描いたものを掲載します。

だいたいこんなかんじです

準同型であることの証明

　以下、対応$x\mathrm{Ker}(\phi) \mapsto \phi(x)$を表す写像を$\psi:G/\mathrm{Ker}(\phi) \rightarrow \mathrm{Im}(\phi)$と書きます。まずはこれが準同型であることを示さなければなりませんが、まあそれは簡単です。

　　見やすくするために$N=\mathrm{Ker}(\phi)$とします。また$\psi(xN)=\phi(x)$であることに注意しておきます。
　さて証明ですが、$\psi((xN)(yN))=\psi(xyN)=\phi(xy)=\phi(x)\phi(y)=\psi(xN)\psi(yN)$です。準同型ですね。

全射であることの証明

　まあこれも簡単です。$y \in \mathrm{Im}(\phi)$なら$\phi(x)=y$となる$x\in G$が取れます。もうお分かりですね。$\psi(x\mathrm{Ker}(\phi))=\phi(x)=y$です。全射！！！

単射であることの証明

　最後になります。$\psi:G/\color{magenta}\mathrm{Ker}(\phi)\color{black} \rightarrow \mathrm{Im}(\phi)$が単射であることを示します。また見やすくするために$N=\color{magenta}\mathrm{Ker}(\phi)\color{black}$とします。ここでは私が重要重要と書きまくっていた定理を使います。（$\mathrm{Ker}$が2つ出るので色分けしています。）

　この定理によると、$\color{blue}\mathrm{Ker}(\psi)\color{black}=\{N\}$を示せばよいです。（$G/\color{magenta}\mathrm{Ker}(\phi)\color{black}=G/N$の単位元は$N$です。）
　$xN \in \color{blue}\mathrm{Ker}(\psi) $、つまり$\psi(xN)=1$であるとします。すると$\phi(x)=\psi(xN)=1$より$x \in \color{magenta}\mathrm{Ker}(\phi)\color{black}=N$がわかるので、$xN=N$がわかります。ということは$\color{blue}\mathrm{Ker}(\psi)\color{black}=\{N\}$が分かってしまいました。単射だ！！！ 　

やったーーーー！！！！

　こうして準同型定理を証明できました！証明自体はそんなに難しくなかったですね。あとは準同型定理を使う問題を実際に解いてみて、この記事をまとめて終わろうと思います。

準同型定理を使おう

もともと同型な写像に適用してみた場合

　「準同型を無理やり全単射にして同型を作る」のが準同型定理です。では、もともと同型だった場合はどうでしょうか。
　同型写像（つまり全単射）$\phi:G\rightarrow G'$を準同型定理の式$G/\mathrm{Ker}(\phi) \cong \mathrm{Im}(\phi)$に適用したいです。

・$\mathrm{Ker}(\phi)$は？
　単射なので単位元のみです。よって左辺は$G/\mathrm{Ker}(\phi)=G/\{1\} \cong G$です。

・$\mathrm{Im}(\phi)$は？
　全射なので$\mathrm{Im}(\phi)=G'$です。

　つまり、$G \cong G'$ です！！！！！何も得られていません！！！！！！！！

$\exp$

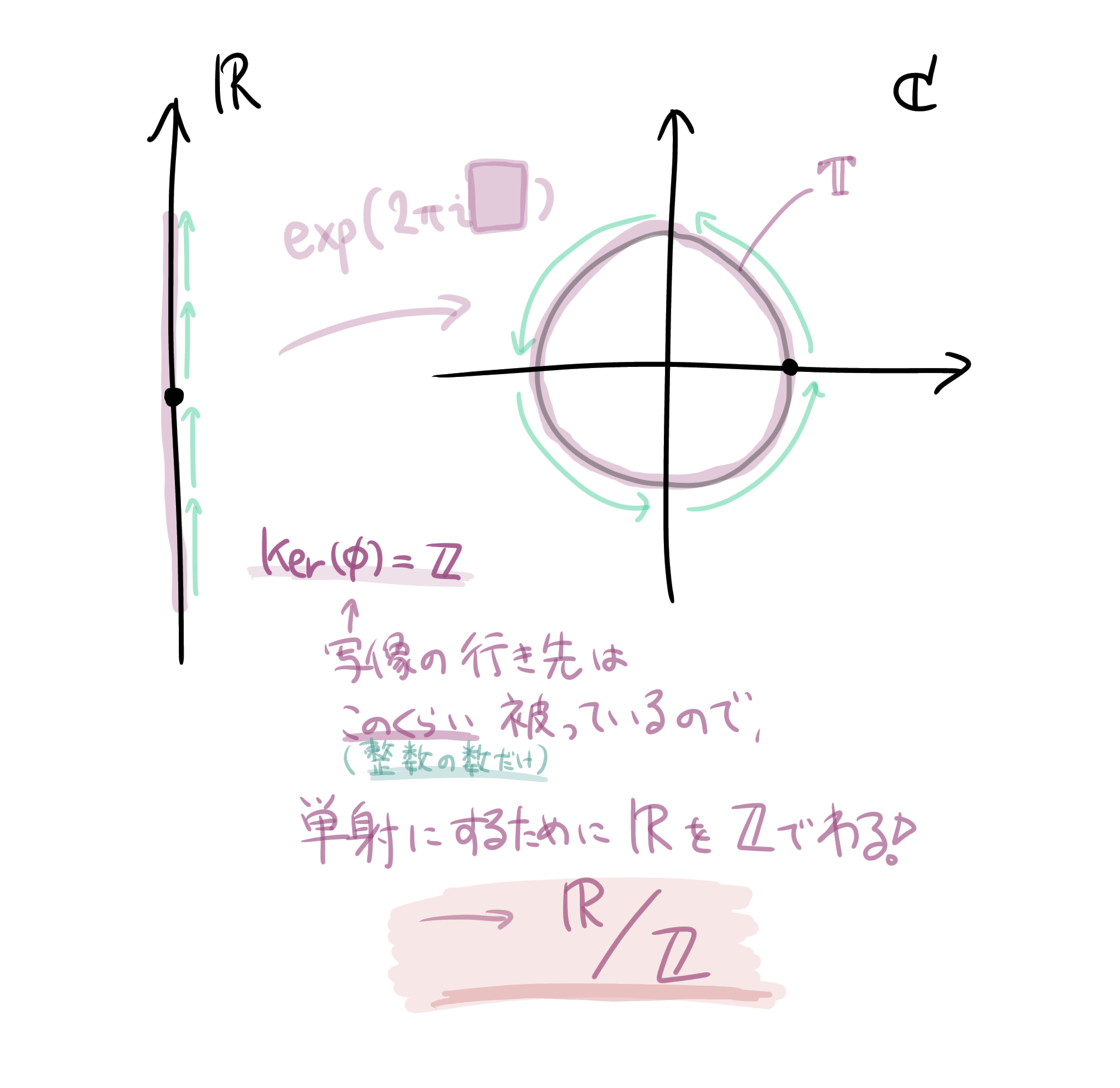
　準同型写像$\phi : \mathbb{R} \rightarrow \mathbb{C} \setminus \{0\}$を、$\phi(\theta)=\exp(2\pi i \theta)$で定めます。ここに適用してみましょう！

・$\mathrm{Ker}(\phi)$は？
　$\exp(2\pi i \theta)=1$となることと$\theta \in \mathbb{Z}$は同値です。よって$\mathrm{Ker}(\phi) = \mathbb{Z}$です。

・$\mathrm{Im}(\phi)$は？
　絶対値が$1$の元全体と対応します。$\mathbb{T}=\{$$z \in \mathbb{C}$$|$$\abs{z}=1$$\}$です。

　さて、これを$G/\mathrm{Ker}(\phi) \cong \mathrm{Im}(\phi)$に適用してみると、$\mathbb{R}/\mathbb{Z} \cong \mathbb{T}$となります。これをトーラス群と呼ぶようです。
トーラス群の図

対称群

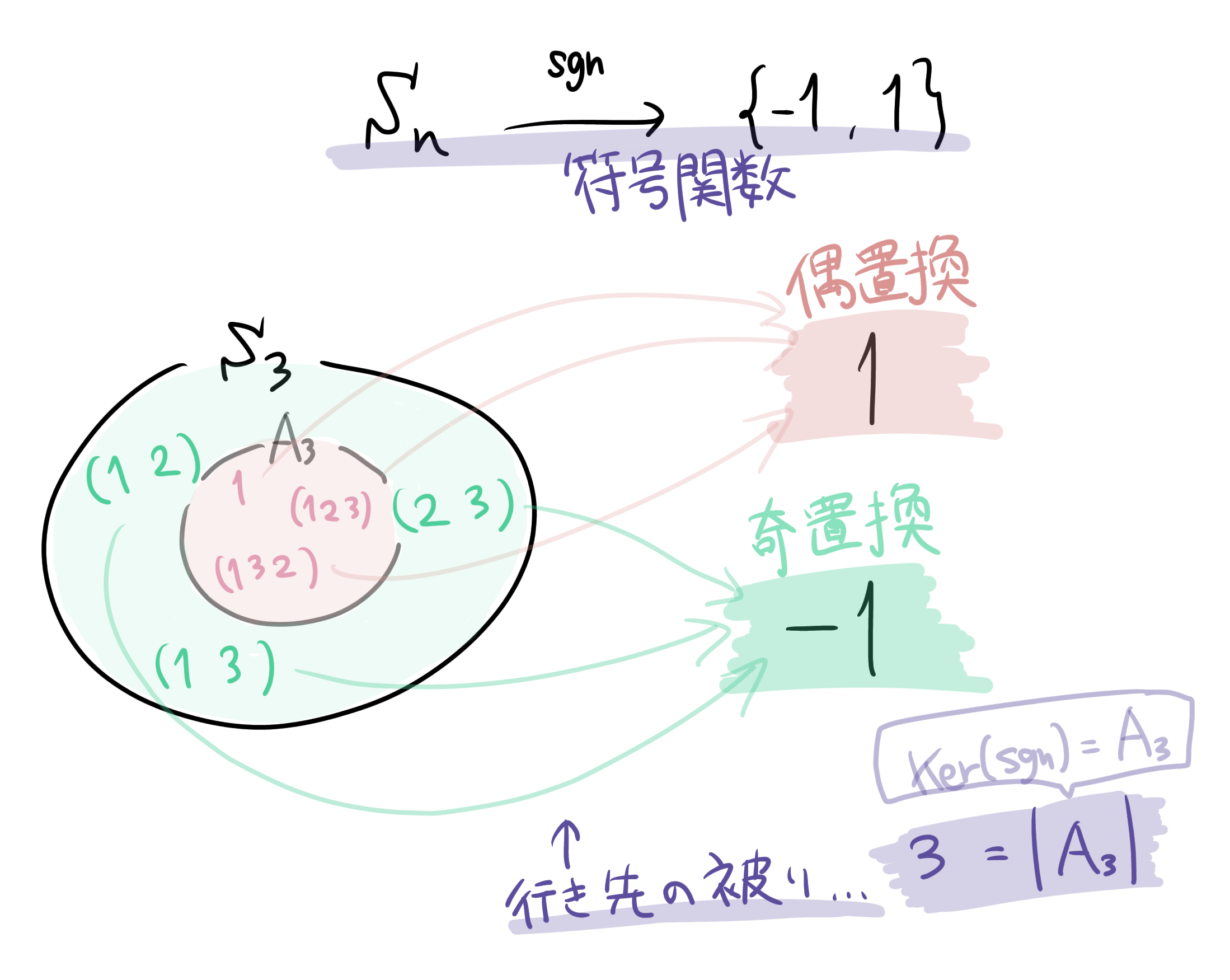
　置換から符号を対応させる準同型$\mathrm{sgn}:S_n \rightarrow \{-1,1\}$を考えてみます。$n$は$2$以上の整数とします。

・$\mathrm{Ker}(\mathrm{sgn})$は？
　置換$\sigma$が$\mathrm{sgn}(\sigma)=1$となることは、$n$次交代群$A_n$の元であることと同値です。（同値というか、そもそも$A_n$の定義を$\mathrm{Ker}(\mathrm{sgn})$で行うのが主流なんですかね？）よって$\mathrm{Ker}(\mathrm{sgn})=A_n$です。

・$\mathrm{Im}(\mathrm{sgn})$は？
　全射なので、$\{-1,1\}$です。

　では、これを$G/\mathrm{Ker}(\phi) \cong \mathrm{Im}(\phi)$に適用してみると、$S_n/A_n \cong \{-1,1\}$となります。

n=3の場合

エンディング

　さて、準同型定理のイメージは掴んでいただけましたでしょうか。$G/\mathrm{Ker}(\phi) \cong \mathrm{Im}(\phi)$という式からもう色々見て取れるのではないでしょうか。ここまでの内容を画像でまとめましたので、図を御覧ください。

これ1枚でマスター！

おしまい！

　ここまで読んでいただきありがとうございます！かな～～～～～り頑張って記事を書きました。GWを3日潰しました。どうでしたでしょうか？準同型定理の理解度は上がりましたでしょうか？
　今までに見てきた準同型定理の説明を見て、こういう説明の仕方をしているものは見たことがないな～～～と思い、（私が見たことがないだけだとは思いますが）いつか書こういつか書こうと思っていたら2年経ってしまいました。今回、なんとか完成させることができて、書き終わった今満足感に包まれています。図もいっぱい書きましたし、力作のつもりです。
　前編後編と割と長かったと思いますが、ここまで読んでいただき本当にありがとうございました。この記事の直感を持った状態で線形代数を見ると、$\mathrm{Ker}(\phi)$の次元が、「線形写像がどれだけ単射でないか」を表しているという見方ができると思います。準同型の核と単射とのつながりがこの記事で一番伝えたかった（？）ことですので、その部分を楽しんでいただけましたのなら幸甚の至りです。

　もし面白かったという方は記事の高評価よろしくお願いします！　それでは～～～