f(x)/(x+t)の積分1
prop2,25
先ず,prop2,25を解きます.
\begin{align}
\int_{-\infty}^{\infty}\ln\left(1+\frac{4\pi^2}
{(e^x-x+\ln\frac\pi2)^2}\right)dx,\int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx
\end{align}
です.
どちらも少し変形してみます
\begin{eqnarray}
\int_{-\infty}^{\infty}\ln\left(1+\frac{4\pi^2}{(e^x-x+\ln\frac\pi2)^2}\right)dx&=&\int_0^{\infty}\ln\left(1+\frac{4\pi^2}{(x-\ln x+\ln\frac\pi2)^2}\right)\frac{dx}{x}\\
&=&\mathrm{Re}\ 2\int_0^{\infty}\left(\ln\left(x-\ln x+\ln\frac{\pi}{2}-2\pi i\right)-\ln\left(x-\ln x+\ln\frac{\pi}{2}\right)\right)\frac{dx}{x}\\
&=&\mathrm{Re}\ 2\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac{\pi}{2}}-\frac{1}{x-\ln x+\ln\frac\pi2-2\pi i}\right)\left(1-\frac1x\right)\ln x\ dx
\end{eqnarray}
次に偏角を$(-\pi,\pi]$として,
\begin{eqnarray}
\int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx&=&\frac{1}{2}\int_{-\pi/2}^{\pi/2} \frac{x^2}{x^2+\ln^2(e^{ix}+e^{-ix})}dx\\
&=&\mathrm{Im}\ \frac{1}{2}\int_{-\pi/2}^{\pi/2}\frac{-x}{\ln(e^{ix}+e^{-ix})+ix}dx\\
&=&\mathrm{Im}\ \frac{1}{2}\int_{-\pi/2}^{\pi/2}\frac{-x}{\ln(e^{2ix}+1)}dx\\
&=&\mathrm{Im}\ \frac18\oint_{|z|=1}\frac{\ln z}{\ln(z+1)}\frac{dz}{z}
\end{eqnarray}
それぞれの課題点を考えてみましょう.
先ず一つ目ですが,最後の式を見るに,偏角を$[0,2\pi)$として$f(z)=\frac{1-\frac1z}{z-\ln z+\ln\frac\pi2}\ln z$とすれば計算できそうに感じますが,これでは大円の経路が発散してしまいます.
つぎに,二つ目は$\ln z$が$z\in\mathbb{R}_{\lt0}$で正則ではないので,そのまま留数定理を用いるということができません.
頑張って計算してみると.
\begin{eqnarray}
\left(\oint_{|z|=1}+\int_{-1+i0}^{-\varepsilon}-\oint_{|z|=\varepsilon}-\int_{-1-i0}^{-\varepsilon}\right)\frac{\ln z}{\ln(z+1)}\frac{dz}{z}&=&0\\
\end{eqnarray}
\begin{eqnarray}
\left(\int_{-1+i0}^{-\varepsilon}-\int_{-1-i0}^{-\varepsilon}\right)\frac{\ln z}{\ln(z+1)}\frac{dz}{z}&=&\int_{-1}^{-\varepsilon}\frac{(\ln(-t)+\pi i)-(\ln(-t)-\pi i)}{\ln(t+1)}\frac{dt}{t}\\
&=&\int_{\varepsilon}^{1}\frac{-2\pi i}{\ln(1-t)}\frac{dt}{t}\\
\end{eqnarray}
\begin{eqnarray}
\oint_{|z|=\varepsilon}\frac{\ln z}{\ln(z+1)}\frac{dz}{z}&=&\oint_{|z|=\varepsilon}\frac{\ln z}{z}\left(\frac{1}{z}+\frac12-\frac{z}{12}+O(z^2)\right)dz\\
&=&i\int_{-\pi}^{\pi}\left(\ln\varepsilon+ix\right)\left(\frac{1}{\varepsilon e^{ix}}+\frac{1}{2}-\frac{\varepsilon e^{ix}}{12}+O(\varepsilon^2)\right)dx\\
&=&\pi i\ln\varepsilon+\frac{2\pi i}{\varepsilon}+O(\varepsilon)
\end{eqnarray}
\begin{eqnarray}
\therefore\oint_{|z|=1}\frac{\ln z}{\ln(z+1)}\frac{dz}{z}&=&\int_{\varepsilon}^{1}\frac{2\pi i}{\ln(1-t)}\frac{dt}{t}+\pi i\ln\varepsilon+\frac{2\pi i}{\varepsilon}+O(\varepsilon)\\
&=&2\pi i\int^{1}\frac{dt}{t\ln(1-t)}\\
&=&2\pi i\left(\int_0^1\frac{1}{t\ln(1-t)}+\frac{1}{t^2}-\frac{1}{2t}dt+1\right)
\end{eqnarray}
最後の積分は計算可能なので値を出すことができました.
しかし,これはかなり難しい計算方法だと思います.
別の簡単な計算方法を紹介します.
\begin{align} \int_0^{\infty}\ln\left(1+\frac{4\pi^2}{(e^x-x+\ln\frac{\pi}{2})}\right)=2\pi^2 \end{align}
$a\in\mathbb{R}_{\gt0}$について,
\begin{align}
I(a):=\int_0^{\infty}\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{dx}{x+a}
\end{align}
\begin{eqnarray}
I(\infty)&=&\lim_{a\to\infty}\int_0^1\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac\pi2}\right)\frac{dx}{x+a}+\int_0^1\left(\frac{1}{x}-\frac{1}{x+\frac1a}\right)\ln\left(1+\frac{2\pi i}{\frac1x+\ln x+\ln\frac\pi2}\right)dx\\
&=&0
\end{eqnarray}
より,
\begin{eqnarray}
I(\infty)-I(a)&=&\int_a^{\infty}I'(t)dt\\
-I(a)&=&-\int_a^{\infty}\int_0^{\infty}\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{dx}{(x+t)^2}dt
\end{eqnarray}
であり,
\begin{eqnarray}
\int_0^{\infty}\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{dx}{(x+t)^2}&=&\left[\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{-1}{x+t}\right]_0^{\infty}
+\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac{\pi}{2}+2\pi i}-\frac{1}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{1-\frac1x}{x+t}dx\\
&=&\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac\pi2+2\pi i}-\frac{1}{x-\ln x+\ln\frac\pi2}\right)\frac{1-\frac1x}{x+t}dx
\end{eqnarray}
です.偏角を$[0,2\pi)$として,
\begin{align}
f(z):=\frac{1-\frac{1}{z}}{z-\ln z+\ln\frac{\pi}{2}+2\pi i}\frac{1}{z+t}
\end{align}
の複素積分を考えます.
これは$z\in\mathbb{R}_{\geq0}$で正則でないので,次のような経路$C$を考えれば,
\begin{align}
\oint_Cf(z)dz=2\pi i\mathrm{Res}...
\end{align}
となります.
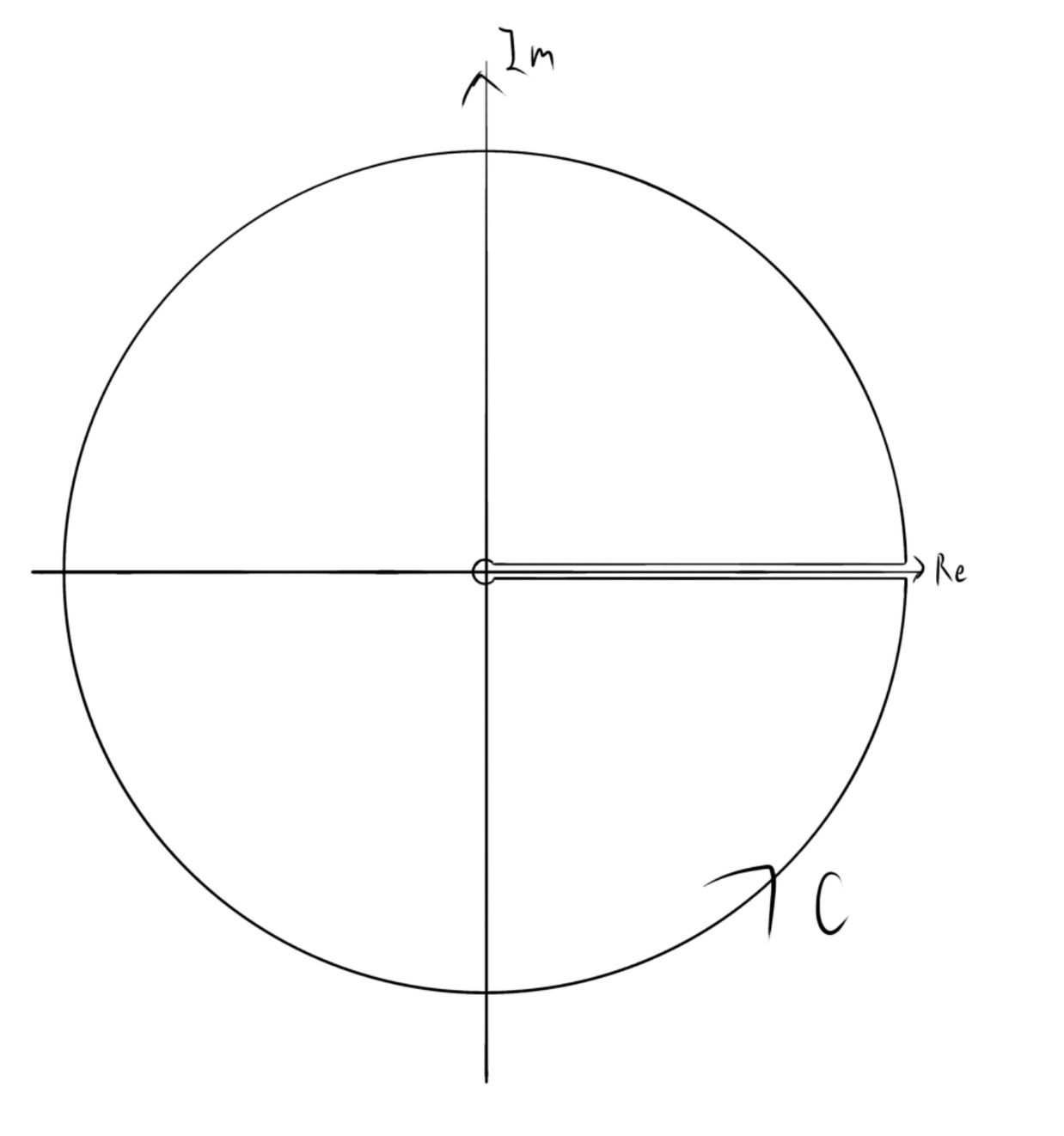
極は$z=-t$がすぐにわかり,少し考えると$z=\frac{\pi}{2}e^{\frac{3\pi i}{2}}$も
\begin{align}
\frac{\pi}{2i}-\left(\frac{3\pi i}{2}+\ln\frac{\pi}{2}\right)+\ln\frac{\pi}{2}+2\pi i=0
\end{align}
なので極であることがわかります.
そのため,
\begin{align}
\oint_Cf(z)dz=2\pi i\left(\frac{1+\frac{1}{t}}{\pi i-t-\ln t+\ln\frac{\pi}{2}}+\frac{1}{t-\frac{\pi i}{2}}\right)
\end{align}
となります.
\begin{eqnarray}
\oint_Cf(z)dz&=&\int_0^{\infty}f(x)-f(xe^{2\pi i})dx+\int_0^{2\pi}f(\infty e^{ix})i\infty e^{ix}dx-\int_0^{2\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx\\
&=&\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac\pi2+2\pi i}-\frac{1}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{1-\frac{1}{x}}{x+t}dx
\end{eqnarray}
なので,
\begin{align}
\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac{\pi}{2}+2\pi i}-\frac{1}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{1-\frac1x}{x+t}dx=2\pi i\left(\frac{1}{t-\frac{\pi i}{2}}-\frac{1+\frac1t}{t+\ln t-\pi i-\ln\frac{\pi}{2}}\right)
\end{align}
であり,
\begin{eqnarray}
I(a)&=&\int_a^{\infty}\int_0^{\infty}\ln\left(1+\frac{2\pi i}{x-\ln x+\ln\frac\pi2}\right)\frac{dxdt}{x+t}\\
&=&\int_a^{\infty}\int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac\pi2+2\pi i}-\frac{1}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{dxdt}{x+t}\\
&=&\int_a^{\infty}2\pi i\left(\frac{1}{t-\frac{\pi i}{2}}-\frac{1+\frac1t}{t+\ln t-\ln\frac{\pi}{2}-\pi i}\right)dt\\
&=&2\pi i\left[\ln\frac{t-\frac{\pi i}{2}}{t+\ln t-\ln\frac{\pi}{2}-\pi i}\right]_a^{\infty}\\
&=&2\pi i\ln\frac{a+\ln a-\ln\frac{\pi}{2}-\pi i}{a-\frac{\pi i}2}
\end{eqnarray}
がわかります.
$a\to+0$とすると,虚部は発散しそうなので実部を取ってみると,
\begin{align}
\int_0^{\infty}\ln\left(1+\frac{4\pi^2}{\left(x-\ln x+\ln\frac{\pi}{2}\right)^2}\right)\frac{dx}{x}=2\pi^2
\end{align}
となり題意が示されました.
$a=1$を考えてみると,
\begin{align}
\int_0^{\infty}\left(\frac{1}{2}\ln\left(1+\frac{4\pi^2}{\left(x-\ln x+\ln\frac{\pi}{2}\right)^2}\right)+i\arctan\frac{2\pi}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{dx}{x+1}\\
=2\pi\left(\arctan\frac{\pi}{1-\ln\frac{\pi}{2}}-\arctan\frac{\pi}{2}\right)+\pi i\ln\frac{\left(1-\ln\frac{\pi}{2}\right)^2+\pi^2}{1+\frac{\pi^2}{4}}
\end{align}
がわかったりします.
\begin{align} \int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx=\frac{\pi}{8}(1-\gamma+\ln2\pi) \end{align}
偏角を$(-\pi,\pi]$します.
先ほどの変形より,
\begin{align}
\int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx=\mathrm{Im}\ \frac18\oint_{|z|=1}\frac{\ln z}{\ln(1+z)}\frac{dz}{z}
\end{align}
です.ここから変形していきます.
\begin{eqnarray}
\oint_{|z|=1}\frac{\ln z}{\ln(1+z)}\frac{dz}{z}&=&\oint_{|z|=1}\left(1-\frac{\ln(1+z)-\ln z}{\ln(1+z)}\right)\frac{dz}{z}\\
&=&\oint_{|z|=1}\left(1-\frac{1}{\ln(1+z)}\int_0^1\frac{dt}{z+t}\right)\frac{dz}{z}\\
&=&2\pi i-\oint_{|z|=1}\int_0^1\frac{1}{z+t}\frac{1}{\ln(1+z)}\frac{dtdz}{z}
\end{eqnarray}
であり,$0\lt t\lt1$において次の積分の経路内は$z=0,-t$以外で正則なので,
\begin{eqnarray}
\oint_{|z|=1}\frac{1}{\ln(1+z)}\frac{dz}{z(z+t)}&=&2\pi i\left(\mathrm{Res}_{z=0}+\mathrm{Res}_{z=-t}\right)\frac{1}{\ln(1+z)}\frac{1}{(z+t)z}\\
&=&2\pi i\lim_{z\to-t}\frac{1}{z\ln(1+z)}+\lim_{\varepsilon\to+0}\int_{-\pi}^{\pi}\frac{i}{\ln(1+\varepsilon e^{ix})}\frac{dx}{t+\varepsilon e^{ix}}\\
&=&-\frac{2\pi i}{t\ln(1-t)}+\lim_{\varepsilon\to+0}i\int_{-\pi}^{\pi}\frac{1}{t\varepsilon e^{ix}}+\frac{t-2}{2t^2}+O(\varepsilon)dx\\
&=&2\pi i\left(\frac{t-2}{2t^2}-\frac{1}{t\ln(1-t)}\right)
\end{eqnarray}
となります.
よって,
\begin{eqnarray}
\int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx&=&\mathrm{Im}\ \frac{1}{8}\oint_{|z|=1}\frac{\ln z}{\ln(1+z)}\frac{dz}{z}\\
&=&\frac{\pi}{4}\left(1+\int_0^1\frac{1}{t\ln(1-t)}-\frac{t-2}{2t^2}dt\right)
\end{eqnarray}
となります.
\begin{eqnarray}
\int_0^1\frac{1}{x\ln(1-x)}+\frac{1}{x^2}-\frac{1}{2x}dx&=&\int_0^1\frac{1}{1-x}\left(\frac{1}{\ln x}-\frac12+\frac{1}{1-x}\right)dx\\
&=&\int_0^{\infty}\frac{1}{e^x-1}\left(-\frac1x-\frac{1}{2}+\frac{e^x}{e^x-1}\right)dx\\
&=&\int_0^{\infty}\frac{e^x}{(e^{x}-1)^2}-\frac{1}{2(e^{x}-1)}-\frac{1}{x(e^x-1)}dx
\end{eqnarray}
これは,前回解説したprop42と同じようにして計算できます.
\begin{align}
I(s):=\int_0^{\infty}\left(\frac{xe^x}{(e^x-1)^2}-\frac{x}{2(e^x-1)}-\frac{1}{e^x-1}\right)e^{-sx}dx
\end{align}
とすれば,
\begin{align}
\int_0^{\infty}\frac{e^x}{(e^x-1)^2}-\frac{1}{2(e^x-1)}-\frac{1}{x(e^x-1)}dx=\int_0^{\infty}I(t)dt
\end{align}
です.そして,
\begin{align}
i(s):=\int_0^{\infty}\left(\frac{x^2e^x}{(e^x-1)^2}-\frac{x^2}{2(e^x-1)}-\frac{x}{e^x-1}\right)e^{-sx}dx
\end{align}
とすれば,
\begin{align}
I(s)=\int_s^{\infty}i(t)dt
\end{align}
です.
\begin{eqnarray}
i(s)&=&\sum_{n\geq0}\int_0^{\infty}\left(x^2ne^{-nx}-\frac{x^2}{2}e^{-(n+1)x}-xe^{-(n+1)x}\right)e^{-sx}dx\\
&=&\sum_{n\geq0}\left(\frac{2n}{(n+s)^3}-\frac{1}{(n+s+1)^3}-\frac{1}{(n+1+s)^2}\right)\\
&=&2\psi^{(1)}(s)+s\psi^{(2)}(s)-\psi^{(1)}(s+1)+\frac{1}{2}\psi^{(2)}(s+1)
\end{eqnarray}
なので,
\begin{eqnarray}
I(s)&=&\left[\psi^{(0)}(t)-\psi^{(0)}(t+1)+t\psi^{(1)}(t)+\frac12\psi^{(1)}(t+1)\right]_s^{\infty}\\
&=&1-\left(-\frac{1}{2s^2}-\frac1s+\left(s+\frac12\right)\psi^{(1)}(s)\right)
\end{eqnarray}
であり,
\begin{eqnarray}
\int_0^{\infty}\frac{e^x}{(e^x-1)^2}-\frac{1}{2(e^x-1)}-\frac{1}{x(e^x-1)}dx&=&\int_0^{\infty}1+\frac{1}{2s^2}+\frac{1}{s}-\left(s+\frac12\right)\psi^{(1)}(s)ds\\
&=&\left[\ln\Gamma(x)+x-\frac{1}{2x}+\ln x-\left(x+\frac12\right)\psi^{(0)}(x)\right]_0^{\infty}\\
&=&\frac{1}{2}+\frac12\ln2\pi-1-\frac12\gamma\\
&=&\frac{\ln2\pi-\gamma-1}{2}
\end{eqnarray}
以上より,
\begin{eqnarray}
\int_0^{\pi/2}\frac{x^2}{x^2+\ln^2(2\cos x)}dx&=&\frac{\pi}{4}\left(1+\int_0^1\left(\frac{1}{x\ln(1-x)}+\frac{1}{x^2}-\frac{1}{2x}\right)dx\right)\\
&=&\frac{\pi}{4}\left(1+\int_0^{\infty}\left(\frac{e^x}{(e^x-1)^2}-\frac{1}{2(e^x-1)}-\frac{1}{x(e^x-1)}\right)dx\right)\\
&=&\frac{\pi}{8}(1+\ln2\pi-\gamma)
\end{eqnarray}
です.
これは僕の最初の記事で出ていますが当時の僕に解けるレベルではなかったです.
f(x)/(x+t)型の積分
今回示すのに用いた変形として重要なのは,
\begin{eqnarray} \int_0^{\infty}\left(\frac{1}{x-\ln x+\ln\frac{\pi}{2}+2\pi i}-\frac{1}{x-\ln x+\ln\frac{\pi}{2}}\right)\frac{1-\frac1x}{x+t}dx&=&2\pi i\left(\frac{1}{t-\frac{\pi i}{2}}-\frac{1+\frac{1}{t}}{t+\ln t-\pi i-\ln\frac{\pi}{2}}\right)\\ \oint_{|z|=1}\frac{1}{\ln(1+z)}\frac{dz}{z(z+t)}&=&2\pi i\left(\frac{t-2}{2t^2}-\frac{1}{t\ln(1-t)}\right) \end{eqnarray}
でした.
どちらも,$\frac{1}{x+t}$を含んだ積分になっています.
このような積分で有名なものとして,Hilbert変換があります.
\begin{align}
H(f)(t):=p.v.\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{f(x)}{x-t}dx
\end{align}
いままでのものを踏まえると,積分区間が$(-\infty,\infty)$以外のものを考えたくなります.
Kの積分を解く
にて次の積分の解法を軽く紹介していました.
\begin{eqnarray}
\int_0^{1}\frac{\kappa(1-x)}{\sqrt x}\frac{dx}{1-xt}&=&\pi\kappa(t)\\
\int_0^1\kappa(x)\kappa(1-x)\frac{dx}{1-xt}&=&\frac{\pi}{2}\kappa(t)^2
\end{eqnarray}
$\mathrm{proof}$
まず偏角を$(-\pi,\pi)$としたとき,$x\in\mathbb{R}_{\gt1}$
\begin{align} \kappa(x\pm0i)=\frac{1}{\sqrt x}\left(\kappa\left(\frac1x\right)\pm i\kappa\left(1-\frac{1}{x}\right)\right) \end{align}
でした.$m,n\in\mathbb{Z}$に対して,
\begin{align} f(z):=\frac{z^m\kappa(z)^n}{z-t} \end{align}
を考えます.$\kappa(z)$が$z\in\mathbb{R}_{\gt1}$で正則でないので,次の経路$C$を考えます.
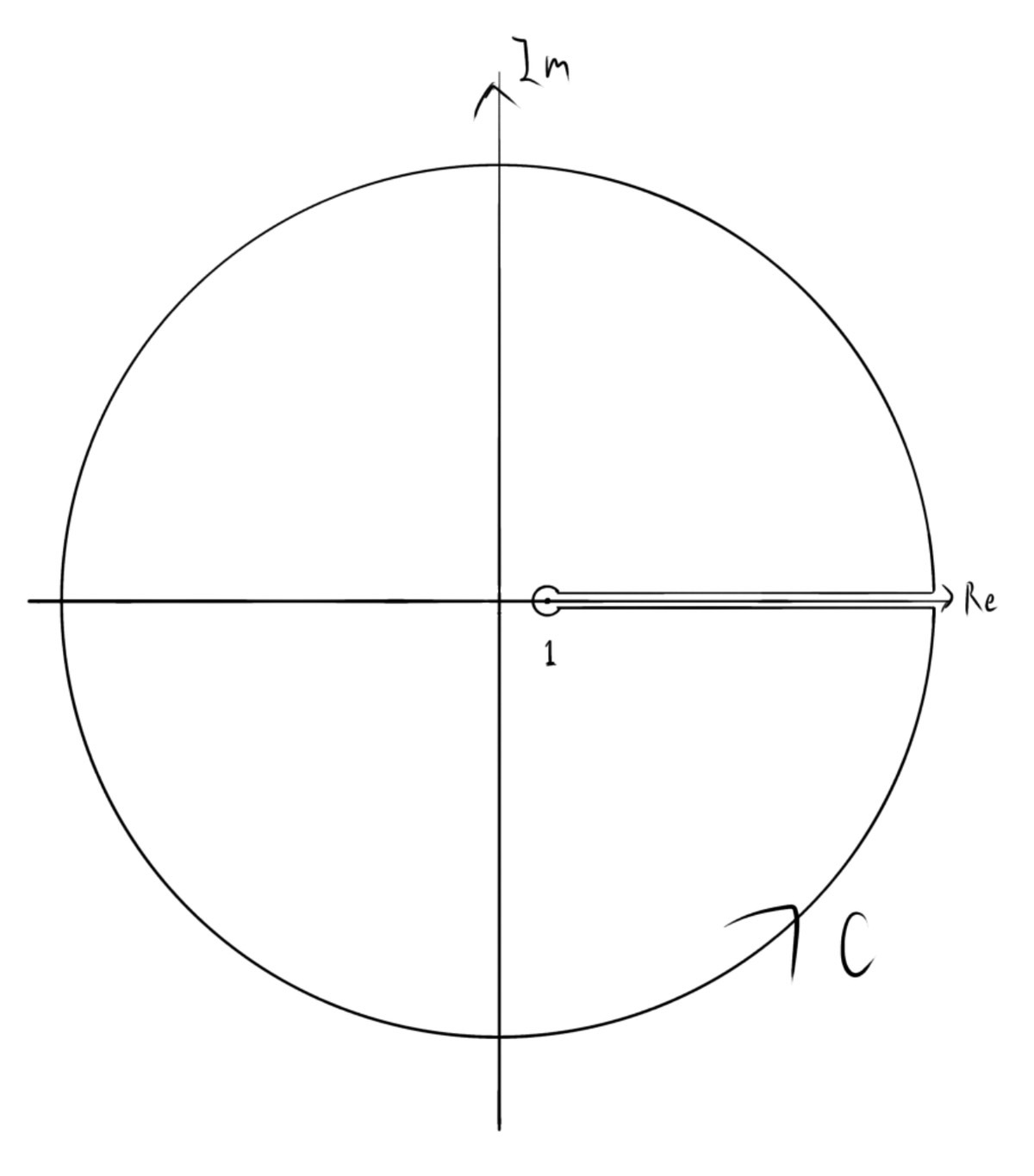
\begin{align} \oint_{C}f(z)dz=\int_1^{\infty}f(x+i0)-f(x-i0)dx+\int_{-\pi}^{\pi}f(\infty e^{ix})\infty ie^{ix}dx-\int_{-\pi}^{\pi}f(1+0e^{ix})0ie^{ix}dx \end{align}
です.
\begin{align} \int_{-\pi}^{\pi}f(\infty e^{ix})\infty ie^{ix}dx=\int_{-\pi}^{\pi}f(1+0e^{ix})0 ie^{ix}dx=0 \end{align}
となる$n,m$に対して,
\begin{eqnarray} \oint_Cf(z)dz&=&\int_1^{\infty}f(x+0i)-f(x-0i)dx\\ &=&\int_1^{\infty}\frac{x^m}{x-t}\left(\left(\kappa\left(\frac{1}{x}\right)+i\kappa\left(1-\frac1x\right)\right)^n-\left(\kappa\left(\frac{1}{x}\right)-i\kappa\left(1-\frac{1}{x}\right)\right)^n\right)\frac{dx}{x^{n/2}} \\ &=&\int_0^1\frac{x^{\frac{n}{2}-m-1}}{1-xt}\left(\left(\kappa\left(x\right)+i\kappa(1-x)\right)^n-\left(\kappa(x)-i\kappa(1-x)\right)^n\right)dx \end{eqnarray}
なので,
\begin{eqnarray} \oint_Cf(z)dz=2\pi i \ t^m\kappa(t)^n+\lim_{\varepsilon\to0}2\pi i\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx \end{eqnarray}
を踏まえると
$m=0,n=1$で
\begin{align} \int_0^1\frac{\kappa(1-x)}{\sqrt x}\frac{dx}{1-xt}=\pi\kappa(t) \end{align}
$m=0,n=2$で
\begin{align} \int_0^1\kappa(x)\kappa(1-x)\frac{dx}{1-xt}=\frac{\pi}{2}\kappa(t)^2 \end{align}
となります.
これも$\frac{1}{x+t}$を含んだ積分といえそうです.
\begin{align}
\int_Af(x)\frac{dx}{x+y}=F(y),\int_Bg(y)\frac{dy}{x+y}=G(x)
\end{align}
に対して,
\begin{align}
\int_A\int_Bf(x)g(y)\frac{dxdy}{x+y}=\int_BF(y)g(y)dy=\int_Af(x)G(x)dx
\end{align}
となるのはかなり有用なのではないでしょうか.
よく見るのは,
\begin{align}
\int\frac{dx}{x+y}=\ln(x+y)+C
\end{align}
であり,これは今回示した積分や,
\begin{align}
\int_0^1\frac{K'(x)\tanh^{-1}x}{x}dx=\pi\beta(2),\int_0^1\frac{K(x)K'(x)}{x}\ln\frac{1}{1-x^2}dx=\frac{7\pi}{8}\zeta(3)
\end{align}
に使われています.
