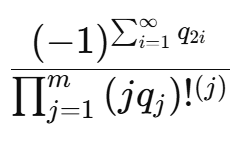任意の関数の関数的平方根を求めよ

関数的平方根

173

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

今回の問題

$f (x)$ の不動点であり、 $f^{\frac{1}{2}} (x)$ の不動点でないものは存在するか。

任意の関数の関数的平方根のテイラー展開をせよ。

ここで $f^{\frac{1}{a}}$ は $\underset{a 回の合成}{\underset{⏟}{f^{\frac{1}{a}} (f^{\frac{1}{a}} (\dots f^{\frac{1}{a}} (x)))}} = f (x)$ となる関数です。

関数的平方根の定義についてはコチラ。
$\sin x$ の関数的平方根についてはコチラ。

問題1

とりあえず前導出した合成不動点定理を確認しましょう。

合成不動点定理

不動点が1つの場合は合成不動点定理ですでに判明しています。

合成不動点定理

方程式 $x = f (x)$ の唯一の解が $α$ であるとき、 $f^{\frac{1}{2}} (α) = α$

$f^{\frac{1}{2}} (α) = β (α \neq β)$ と仮定する。
$\begin{array}{rcl} f^{\frac{1}{2}} (f^{\frac{1}{2}} (α)) & = & f (α) \\ f^{\frac{1}{2}} (β) & = & α \end{array}$
さらに、 $f^{\frac{1}{2}} (f^{\frac{1}{2}} (β)) = f (β)$ なので、
$\begin{array}{rcl} f^{\frac{1}{2}} (f^{\frac{1}{2}} (β)) & = & f (β) \\ f^{\frac{1}{2}} (α) & = & f (β) \\ β & = & f (β) \end{array}$
これは $α$ が $x = f (x)$ の唯一の解であることに矛盾。
よって $f^{\frac{1}{2}} (α) = α$

この証明は不動点が複数あるとき次のようにとらえられます。

$f (α) = α, f^{\frac{1}{2}} (α) = β$ であるとき、 $f (β) = β$

そもそも $f^{\frac{1}{2}} (α) = β (α \neq β)$ となるものが存在するかわかりませんが...

周期点

とりあえず、 $f^{\frac{1}{2}} (α) = β (α \neq β)$ となるものが存在すると仮定します。

周期点

関数 $f$ の $n$ 回合成を $f^{n} (x) (n \in N)$ とする。
ある $α$ において $f^{n} (α) = α$ となるとき、 $α$ を $n$ 周期点とよぶ。

すると、次のようなことが分かります。

$f (x)$ の不動点は $f^{\frac{1}{2}} (x)$ の不動点か $2$ 周期点である。

$f (α) = α$ とする。 $f^{\frac{1}{2}} (f^{\frac{1}{2}} (α)) = α$ を満たす必要があるから、

$f^{\frac{1}{2}} (α) = α$ か ${\begin{cases} f^{\frac{1}{2}} (α) = β \\ f^{\frac{1}{2}} (β) = α \end{cases}$ 　のどちらかである。( $α \neq β$ )

さらに定理2より、 $f (β) = β$ である。

同じようにして $f (x)$ の不動点は $f^{\frac{1}{a}} (x)$ の不動点か、 $a$ 周期点であることが証明できます。

$α$ を $f (x)$ の不動点の1つであるとする。

${\begin{cases} f^{\frac{1}{2}} (α) = β \\ f^{\frac{1}{2}} (β) = α \end{cases}$ 　ならば、 $f^{'} (α) = f^{'} (β)$

$f^{\frac{1}{2}} (f^{\frac{1}{2}} (x)) = f (x)$ の両辺を微分すると、

$f^{\frac{1}{2}}^{'} (x) f^{\frac{1}{2}}^{'} (f^{\frac{1}{2}} (x)) = f^{'} (x)$

$α$ を代入すると、

$\begin{array}{rcl} f^{\frac{1}{2}}^{'} (α) f^{\frac{1}{2}}^{'} (f^{\frac{1}{2}} (α)) & = & f^{'} (α) \\ f^{\frac{1}{2}}^{'} (α) f^{\frac{1}{2}}^{'} (β) & = & f^{'} (α) \end{array}$

$β$ を代入すると、
$\begin{array}{rcl} f^{\frac{1}{2}}^{'} (α) f^{\frac{1}{2}}^{'} (f^{\frac{1}{2}} (β)) & = & f^{'} (β) \\ f^{\frac{1}{2}}^{'} (β) f^{\frac{1}{2}}^{'} (α) & = & f^{'} (β) \end{array}$
よって、 $f^{'} (α) = f^{'} (β)$

つまり、 $f (x)$ の不動点が $f^{\frac{1}{2}} (x)$ の $2$ 周期点になることは今のところほとんどないといえるでしょう。

問題2

$\sin x$ の分解の時のように、微分して求めます。 $f (x)$ の不動点を $Q$ とします。
とりあえず $f^{\frac{1}{2}} (Q) = Q$ を仮定します。
すると、次のようにテイラー展開されます。

不動点周りで $f^{\frac{1}{2}} (x)$ は次のようにテイラー展開される。

$f^{\frac{1}{2}} (x) = \sum_{n = 0}^{\infty} \frac{Q_{n}}{n!} (x - Q)^{n}$

$Q_{10}$ までを記します。とても見づらいですがご了承ください。


$Q_{0}$	$Q$	$Q$
$Q_{1}$	$\sqrt{f^{'} (Q)}$	$\sqrt{f^{'} (Q)}$
$Q_{2}$	$\frac{f^{″} (Q)}{f^{'} (Q) + Q_{1}}$	$\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}}$
$Q_{3}$	$\frac{f^{‴} (Q) - 3 Q_{1} Q_{2}^{2}}{Q_{1}^{3} + Q_{1}}$	$\frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}}$
$Q_{4}$	$\frac{f^{⁗} (Q) - 3 Q_{2}^{3} - 6 Q_{3} Q_{1}^{2} Q_{2} - 4 Q_{3} Q_{1} Q_{2}}{Q_{1}^{4} + Q_{1}}$	$\frac{f^{⁗} (Q) - 3 {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{3} - 6 (\frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}}) (\sqrt{f^{'} (Q)})^{2} \frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}} - 4 (\frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}}) \sqrt{f^{'} (Q)} \frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}}}{(\sqrt{f^{'} (Q)})^{4} + \sqrt{f^{'} (Q)}}$
$Q_{5}$	$\frac{(f^{'''''} (Q) - 10 Q_{3} Q_{3} Q_{1}^{2} - 5 Q_{4} Q_{1} Q_{2} - 15 Q_{3} Q_{1} Q_{2}^{2} - 10 Q_{2} (Q_{4} Q_{1}^{3} + Q_{3} Q_{2}))}{Q_{1}^{5} + Q_{1}}$	$\frac{f^{'''''} (Q) - 10 {(\frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}})}^{2} f^{'} (Q) - 5 (\frac{f^{⁗} (Q) - 3 {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{3} - 6 \frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}} f^{'} (Q) \frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}} - 4 \frac{f^{‴} (Q) - 3 \sqrt{f^{'} (Q)} {(\frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}})}^{2}}{(\sqrt{f^{'} (Q)})^{3} + \sqrt{f^{'} (Q)}} \sqrt{f^{'} (Q)} \frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}}}{f^{'} (Q)^{2} + \sqrt{f^{'} (Q)}}) \sqrt{f^{'} (Q)} \frac{f^{″} (Q)}{f^{'} (Q) + \sqrt{f^{'} (Q)}}}{f^{'} (Q)^{5 / 2} + \sqrt{f^{'} (Q)}}$
$Q_{6}$	$\frac{(f^{''''''} (Q) - 15 Q_{3} Q_{2}^{3} - 20 Q_{3} Q_{4} Q_{1}^{3} - 15 Q_{3} Q_{4} Q_{1}^{2} - 45 Q_{4} Q_{1}^{2} Q_{2}^{2} - 15 (Q_{5} Q_{1}^{4} + 4 Q_{3} Q_{3} Q_{1}) Q_{2} - Q_{2} (10 Q_{3}^{2} + 6 Q_{5} Q_{1} + 15 Q_{4} Q_{2}))}{Q_{1}^{6} + Q_{1}}$	とても長い式
$Q_{7}$	$\frac{f^{'''''''} (Q) - 35 Q_{4} Q_{4} Q_{1}^{3} - 35 Q_{3} Q_{5} Q_{1}^{4} - 21 Q_{3} Q_{5} Q_{1}^{2} - 35 Q_{3} Q_{4} Q_{2} - 105 Q_{4} Q_{1} Q_{2}^{3} - 7 Q_{1} (10 Q_{3} Q_{3}^{2} + Q_{6} Q_{2}) - 105 (Q_{3} Q_{3} Q_{1}^{3} + Q_{5} Q_{1}^{3}) Q_{2}^{2} - 21 Q_{2} (Q_{6} Q_{1}^{5} + Q_{5} Q_{2} + 10 Q_{3} Q_{4} Q_{1}^{2} + 5 Q_{3} Q_{4} Q_{1})}{Q_{1}^{7} + Q_{1}}$	めっちゃ長い式
$Q_{8}$	$\frac{f^{''''''''} (Q) - (35 Q_{4}^{2} Q_{2} + 105 Q_{4} Q_{2}^{4} + 56 Q_{3} Q_{6} Q_{1}^{5} + 70 Q_{4} Q_{5} Q_{1}^{4} + 56 Q_{4} Q_{5} Q_{1}^{3} + 56 Q_{3} Q_{5} Q_{2} + 420 Q_{5} Q_{1}^{2} Q_{2}^{3} + 28 (Q_{3} Q_{6} + 10 Q_{4} Q_{3}^{2}) Q_{1}^{2} + 8 Q_{1} (Q_{7} Q_{2} + 35 Q_{3} Q_{3} Q_{4}) + 210 (Q_{6} Q_{1}^{4} + Q_{3} Q_{4} + 4 Q_{3} Q_{4} Q_{1}) Q_{2}^{2} + 28 Q_{2} (10 Q_{3}^{2} Q_{3} + Q_{7} Q_{1}^{6} + Q_{6} Q_{2} + 15 Q_{4} Q_{4} Q_{1}^{2} + 20 Q_{3} Q_{5} Q_{1}^{3} + 6 Q_{3} Q_{5} Q_{1}))}{Q_{1}^{8} + Q_{1}}$	ものすごく長い式
$Q_{9}$	$\frac{f^{'''''''''} (Q) - (280 Q_{3}^{4} + 36 Q_{7} Q_{2}^{2} + 126 Q_{5}^{2} Q_{1}^{4} + 36 Q_{8} Q_{1}^{7} Q_{2} + 126 Q_{4} Q_{5} Q_{2} + 378 Q_{3} Q_{5} Q_{2}^{2})}{Q_{1}^{9} + Q_{1}} - \frac{126 Q_{1}^{5} (3 Q_{7} Q_{2}^{2} + Q_{4} Q_{6}) + 84 Q_{1}^{3} (Q_{4} Q_{6} + 15 Q_{6} Q_{2}^{3} + 15 Q_{4} Q_{5} Q_{2})}{Q_{1}^{9} + Q_{1}} - \frac{840 Q_{3}^{2} (Q_{5} Q_{1}^{3} + 3 Q_{4} Q_{1} Q_{2}) + 36 Q_{1}^{2} (Q_{3} Q_{7} + 21 Q_{4} Q_{5} Q_{2})}{Q_{1}^{9} + Q_{1}} - \frac{9 Q_{1} (Q_{8} Q_{2} + 105 Q_{5} Q_{2}^{4} + 210 Q_{4}^{2} Q_{2}^{2} + 7 Q_{3} (5 Q_{4}^{2} + 4 Q_{6} Q_{2}))}{Q_{1}^{9} + Q_{1}} - \frac{84 Q_{3} (Q_{7} Q_{1}^{6} + Q_{6} Q_{2} + 15 Q_{4} Q_{2}^{3} + 15 Q_{4}^{2} Q_{1}^{2} + 6 Q_{3} Q_{5} Q_{1} + 45 Q_{5} Q_{1}^{2} Q_{2}^{2} + 15 (Q_{6} Q_{1}^{4} + Q_{3} Q_{4}) Q_{2})}{Q_{1}^{9} + Q_{1}}$	想像できないぐらい長い式
$Q_{10}$	$\frac{f^{''''''''''} (Q) - 126 Q_{5}^{2} Q_{2} - 945 Q_{5} Q_{2}^{5} - 1575 Q_{4}^{2} Q_{4} Q_{1}^{2} - 10 Q_{9} Q_{1} Q_{2} - 45 Q_{3} Q_{8} Q_{1}^{2} - 210 Q_{4} Q_{7} Q_{1}^{6} - 120 Q_{4} Q_{7} Q_{1}^{3} - 252 Q_{5} Q_{6} Q_{1}^{5} - 210 Q_{5} Q_{6} Q_{1}^{4} - 210 Q_{4} Q_{6} Q_{2} - 4725 Q_{6} Q_{1}^{2} Q_{2}^{4} - 2800 Q_{3}^{3} Q_{4} Q_{1} - 3150 (Q_{4} Q_{4} + Q_{7} Q_{1}^{4}) Q_{2}^{3} - 1260 Q_{3} Q_{4} Q_{5} Q_{1} - 2100 Q_{3}^{2} (Q_{6} Q_{1}^{4} + Q_{3} Q_{4} + 3 Q_{4} Q_{2}^{2} + 6 Q_{5} Q_{1}^{2} Q_{2})}{Q_{1}^{10} + Q_{1}}$	とーっても長いんじゃない？多分。

はい。こんな感じです。もう二度と打ちたくありません。
意外と完全ランダムという感じではなく、分母には規則性があります。
これを使えば、大体の関数の関数的平方根を近似することができます。

次のグラフは $x^{2} - 1$ に適用したものです。 !FORMULA[88][1114237592][0]に適用したもの $x^{2} - 1$ に適用したもの
赤は $x^{2} - 1$ 、青は関数的平方根の近似 $(x > 0)$ 、緑はその合成、黒は $x^{\sqrt{2}} - 0.3$ です。
ちなみに不動点は $x = φ$ (黄金数)です。