え!!　交換子だけでルービックキューブを!?

ルービックキューブの可解な配置のうち半数は交換子だけで揃えることができ，残りの半数は任意の面をこっそり$90$度回せば交換子だけで揃えられる配置になるので，実質「出来らあっ！」ということになります．

誤りなどありましたらご指摘・ご教示くださると嬉しいです．

ルービックキューブ群と拡張ルービックキューブ群

ルービック変換とルービックキューブ群

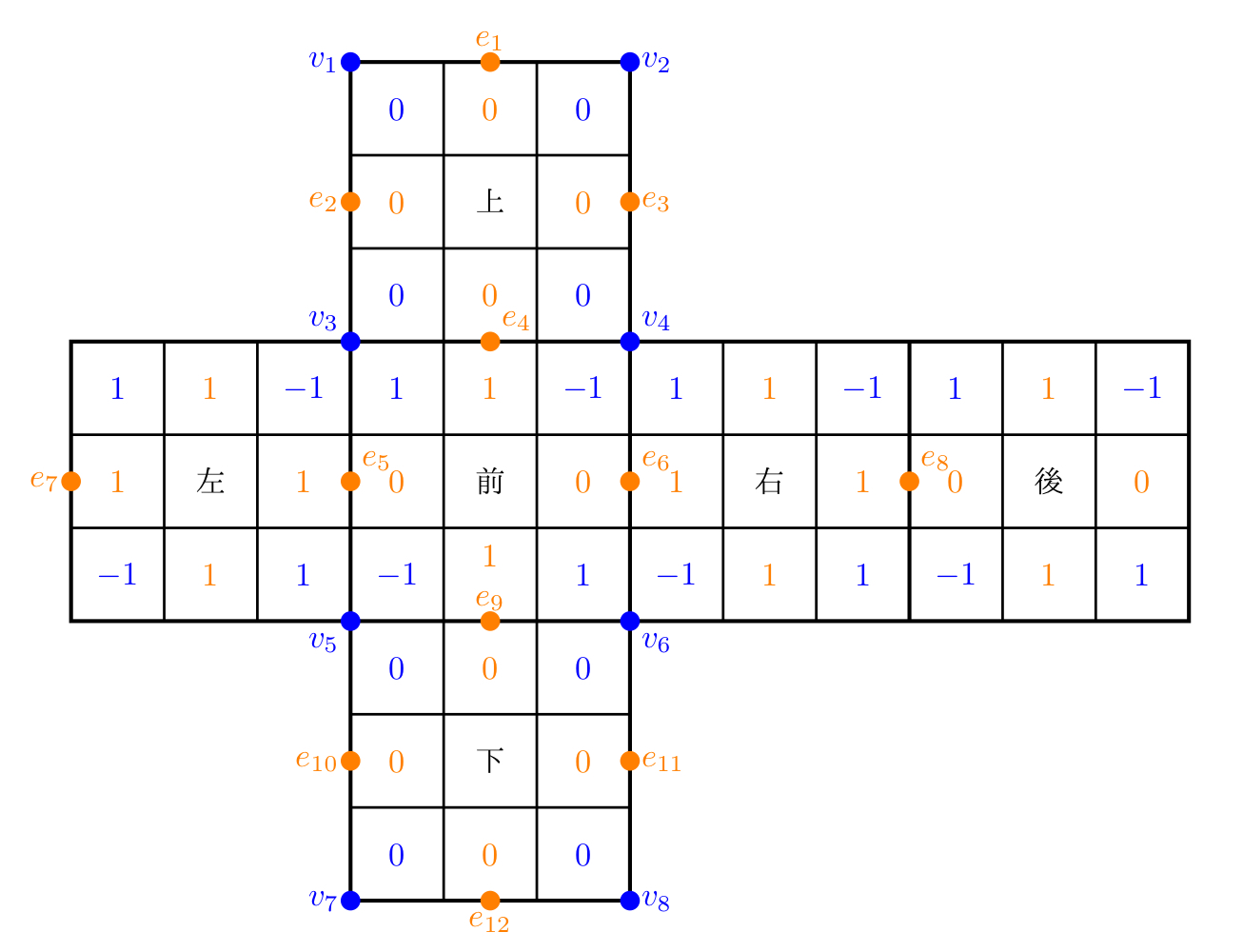ルービックキューブの「展開図」

雑な定義ですが，意味するところは伝わるかと思います．

我々がルービックキューブを揃えるときに行なっているのは，スクランブル$g \in G_{\mathrm{rubik}}$で崩されたルービックキューブに対してうまいことルービック変換$g^{-1} \in G_{\mathrm{rubik}}$を見つけることに他なりません．

拡張ルービック変換と拡張ルービックキューブ群

ところで，ルービックキューブを揃える一番簡単な方法は，一旦分解してから組み立てるというものでしょう．このような操作を考えることは（数学的には）何ら問題がないので，しばらくおおらかに行くことにします．

ルービックキューブを分解してから組み立てるという操作はある置換$\gamma \in S_{48}$に対応します．実際にルービックキューブを観察すると以下のことがわかります．

コーナーキューブについて

• $\gamma(V \times (\mathbb{Z}/3)) \subset V \times (\mathbb{Z}/3)$;
• 任意の$v \in V \times (\mathbb{Z}/3)$に対して，$\pi_{V}(\gamma(v))$は$\pi_{\mathbb{Z}/3}(v)$に依らない．

ただし$\pi_{X}$は$X$への射影です．

これらのことから，$\gamma$は全単射$\gamma_{V} \colon V \to V$および$\{\pi_{V}(v)\} \times (\mathbb{Z}/3) \to \{\pi_{V}(\gamma(v))\} \times (\mathbb{Z}/3)$を誘導することがわかります．後者について次が成り立ちます：

• 全単射$\mathbb{Z}/3 \cong_{\mathrm{Set}} \{\pi_{V}(v)\} \times (\mathbb{Z}/3) \to \{\pi_{V}(\gamma(v))\} \times (\mathbb{Z}/3) \cong_{\mathrm{Set}} \mathbb{Z}/3$は$3$次対称群の元として偶置換である．

エッヂキューブについて

同様に次が成り立ちます：

• $\gamma(E \times (\mathbb{Z}/2)) \subset E \times (\mathbb{Z}/2)$;
• 任意の$e \in E \times (\mathbb{Z}/2)$に対して，$\pi_{E}(\gamma(e))$は$\pi_{\mathbb{Z}/2}(e)$に依らない．

逆にこれら5条件を満たす置換はルービックキューブを分解してから組み立てるという操作に対応しています．

基本変換は拡張ルービック変換なので，$G_{\mathrm{rubik}}$は$\Gamma_{\mathrm{rubik}}$の部分群です．

拡張ルービック変換の作用を詳しく見ていきましょう．

コーナーキューブについて

写像$p_{V} \colon \Gamma_{\mathrm{rubik}} \to S_{8}$を
$$ p_{V}(\gamma) \colon \{1,\ldots,8\} \cong_{\mathrm{Set}} V \stackrel{\gamma_{V}}{\longrightarrow} V \cong_{\mathrm{Set}} \{1,\ldots,8\} $$
で定めます．$\gamma_{V}$の定義から$p_{V}$は準同型です．

また，拡張ルービック変換$\gamma$と$i \in \{1, \ldots, 8\}$に対して，$o_{V}(\gamma)_{i} \in \mathbb{Z}/3$を
$$ \gamma(v_{p_{V}(\gamma^{-1})(i)},0) = (v_{i},o_{V}(\gamma)_{i}) $$
で定め，この値を$\gamma$による$v_{i}$の回転数といいます．
コーナーキューブの回転
$\gamma$から誘導される全単射$\{v_{p_{V}(\gamma^{-1})(i)}\} \times (\mathbb{Z}/3) \to \{v_{i}\} \times (\mathbb{Z}/3)$が偶置換であることから，任意の$n \in \mathbb{Z}/3$に対して
$$ \gamma(v_{p_{V}(\gamma^{-1})(i)},n) = (v_{i},n + o_{V}(\gamma)_{i}) $$
が成り立つことに注意します．

写像$o_{V} \colon \Gamma_{\mathrm{rubik}} \to (\mathbb{Z}/3)^{8}$を
$$ o_{V}(\gamma) = (o_{V}(\gamma)_{1},\ldots,o_{V}(\gamma)_{8}) $$
で定めます．

$o_{V}$は（残念ながら？）準同型ではないのですが，次が成り立ちます：

半直積の積の定義から次が成り立ちます．

エッヂキューブについて

同様にして準同型$p_{E} \colon \Gamma_{\mathrm{rubik}} \to S_{12}$と，$\gamma$による$e_{j}$の反転数$o_{E}(\gamma)_{j} \in \mathbb{Z}/2$が定まります．そこで写像$o_{E} \colon \Gamma_{\mathrm{rubik}} \to (\mathbb{Z}/2)^{12}$を
$$ o_{E}(\gamma) = (o_{E}(\gamma)_{1},\ldots,o_{E}(\gamma)_{12}) $$
で定めます．

$o_{E}$についても同様に次が成り立ちます：

以上の考察から，準同型
$$ \Phi_{\mathrm{rubik}} := (p_{V}, o_{V}, p_{E}, o_{E}) \colon \Gamma_{\mathrm{rubik}} \to (S_{8} \ltimes (\mathbb{Z}/3)^{8}) \times (S_{12} \ltimes (\mathbb{Z}/2)^{12}) $$
が定まります．これが全単射であることは容易に納得できると思います．

これで拡張ルービックキューブ群の構造がわかりました．とくにその位数は$3^{8} \cdot 8! \cdot 2^{12} \cdot 12! = 2^{29} \cdot 3^{15} \cdot 5^{3} \cdot 7^{2} \cdot 11 \sim 5.2 \times 10^{20}$です．

可能配置

ここでルービックキューブ自体に目を向けてみると，混ぜられたルービックキューブの状態は

• コーナーキューブの位置（$8!$通り）
• コーナーキューブそれぞれの向き（$3$通りづつ）
• エッヂキューブの位置（$12!$通り）
• エッヂキューブそれぞれの向き（$2$通りづつ）

で記述できることに気づきます．

集合$\mathcal{C}$と群$(S_{8} \ltimes (\mathbb{Z}/3)^{8} ) \times (S_{12} \ltimes (\mathbb{Z}/2)^{12})$を適宜混同することで$\Gamma_{\mathrm{rubik}}$の$\mathcal{C}$への作用を定めることができます：
$$ c \cdot \gamma := c \Phi_{\mathrm{rubik}}(\gamma);\ c \in \mathcal{C}, \gamma \in \Gamma_{\mathrm{rubik}}. $$
この作用は（当然）自由かつ推移的なので写像$\Gamma_{\mathrm{rubik}} \to \mathcal{C}; \gamma \mapsto I \cdot \gamma$は全単射です．さらに
\begin{align} I \cdot \gamma &= (\mathrm{id},0,\mathrm{id},0) \cdot (p_{V}(\gamma), o_{V}(\gamma), p_{E}(\gamma), o_{E}(\gamma))\\ &= (p_{V}(\gamma), o_{V}(\gamma), p_{E}(\gamma), o_{E}(\gamma))\\ &= \Phi_{\mathrm{rubik}}(\gamma) \end{align}
となるので，$\Phi_{\mathrm{rubik}}$によって操作$\gamma$と状態$I \cdot \gamma$とが同一視できることがわかります．

ルービックキューブの基本定理

その名の通り，可解配置とはルービック変換のみで揃えることのできるルービックキューブの配置のことです．したがって，混ぜられた状態のルービックキューブが与えられたとき，それが可解配置であるかどうか（を判定する方法）が問題になります．

ここではまず必要性のみ証明します．十分性の証明は小キューブの動かし方について考察してから行なうことにします．

小キューブを思いのままに動かすには

数学的準備：交換子による作用について

集合$X$に群$G$が右から作用している状況を考えます．元$g \in G$に対して

• $X^{g} = \{x \in X \mid x \cdot g = x \}$;
• $\mathrm{supp}(g) = X \smallsetminus X^{g} = \{x \in X \mid x \cdot g \neq x\}$

とおきます．これらは$g$の作用に関して閉じており，また$X^{g} = X^{g^{-1}}$，$\mathrm{supp}(g) = \mathrm{supp}(g^{-1})$が成り立ちます．

さらに，$g, h \in G$に対して

• $X_{g,h} = \mathrm{supp}(g) \cap \mathrm{supp}(h)$
• $X(g,h) = X_{g,h} \cup (X_{g,h} \cdot g^{-1}) \cup (X_{g,h} \cdot h^{-1})$

とおきます．

したがって，交換子$[g,h]$による作用を考える場合，部分集合$X(g,h)$への影響だけ考えればよいことになります．

3点交換

2ヶ所での同時置換

3点交換のときと同様に，仮定を満たす元の組がひとつでも見つかればそれらの共軛に対しても同じことが成り立ちます：

小キューブの3点交換

小キューブの2点交換は不可能でしたから，3点交換を考えることにします．

$X = V \cup E$とおきます．ルービックキューブ群$G_{\mathrm{rubik}}$は準同型$p_V \colon G_{\mathrm{rubik}} \to S_{8} \subset S_{20}$および$p_{E} \colon G_{\mathrm{rubik}} \to S_{12} \subset S_{20}$を通して$X$に作用していました．

$a, b, c \in X$を相異なるコーナーキューブ（resp. エッヂキューブ）とします．3点交換の原理より，その条件を満たす$g, h \in G_{\mathrm{rubik}}$をうまく見つけることができれば（向きを無視した）3点交換$a \mapsto b \mapsto c \mapsto a$が実現できます：

詳しく（？）は J Perm氏の動画 （ここでは向きも考慮に入れています）を参照してください．

コーナーキューブの3点交換

任意の3つのコーナーキューブを$v_{1}, v_{2}, v_{4}$に持って来られることはルービックキューブを少しいぢればわかるので，$v_{1}, v_{2}, v_{4}$の3点交換さえ実現できればよいことになります．

たとえば，$g = R, h = U^{-1}L^{-1}U$とおくと，$X_{g,h} = \{v_{2}\},\ X_{g,h} \cdot g^{-1} = \{v_{4}\},\ X_{g,h} \cdot h^{-1} = \{v_{1}\}$となることが（実際にルービックキューブを回すことで）わかります．よって，$\cdot [g,h]$は3点交換$v_{4} \mapsto v_{2} \mapsto v_{1} \mapsto v_{4}$を行ないます．

エッヂキューブの3点交換

任意の3つのエッヂキューブを$e_{1}, e_{4}, e_{9}$に持って来られることはルービックキューブを少しいぢればわかるので，$e_{1}, e_{4}, e_{9}$の3点交換さえ実現できればよいことになります．

たとえば，$g = RF^{2}R^{-1}, h = LU^{2}L^{-1}$とおくと，$X_{g,h} = \{e_{4}\},\ X_{g,h} \cdot g^{-1} = \{e_{9}\},\ X_{g,h} \cdot h^{-1} = \{e_{1}\}$となることがわかります．よって，$\cdot [g,h]$は3点交換$e_{9} \mapsto e_{4} \mapsto e_{1} \mapsto e_{9}$を行ないます．

小キューブの回転・反転

続いて，コーナーキューブの回転，およびエッヂキューブの反転について考えます．

$X = (V \times (\mathbb{Z}/3)) \cup (E \times (\mathbb{Z}/2))$とおきます．ルービックキューブ群$G_{\mathrm{rubik}}$は$X$に作用しているのでした．ひとつの小キューブだけの回転・反転は不可能でしたから，ふたつ（以上）の小キューブを同時に回転・反転させることを考えましょう．以下，たとえば$(v_{1}, 1)$を$v_{1}^{+}$と略記します．

コーナキューブの回転

$g = [R,U]^{2}, h = ULU^{-1}$とおきます．このとき，$X_{g,h} = \{v_{4}^{0}, v_{4}^{+}, v_{4}^{-}\} = X_{g,h} \cdot g^{-1},\ X_{g,h} \cdot h^{-1} = \{v_{3}^{0}, v_{3}^{+}, v_{3}^{-}\}$となることがわかります．よって，$\cdot [g,h]$はコーナーキューブ$v_{3}, v_{4}$の回転のみを行ないます．とくに
$$ v_{3}^{0} \mapsto v_{3}^{-},\ v_{4}^{0} \mapsto v_{4}^{+} $$
となることが実際に確かめられます．

さらに，命題11より，$[g,h]$とその共軛を用いることで，コーナーキューブ$v_{1}, v_{3}, v_{5}, v_{7}$は自由に回転できることがわかります（ただし，総回転数が保存する必要はあります）．

また，$g' = [L,D]^{2}, h' = DRD^{-1}$とおくと，$[g',h']$とその共軛を用いることで，コーナーキューブ$v_{5}, v_{6}, v_{7}, v_{8}$は自由に回転できることがわかります．

エッヂキューブの反転

$g = RUD^{-1}F^{2}U^{2}D^{2}BU, h = U^{-1}$とおきます．このとき，$X_{g,h} = \{e_{3}^{0}, e_{3}^{+}\} = X_{g,h} \cdot g^{-1}, X_{g,h} \cdot h^{-1} = \{e_{4}^{0}, e_{4}^{+}\}$となることがわかります．よって，$\cdot [g,h]$はエッヂキューブ$e_{3}, e_{4}$の反転のみを行ないます．さらに，命題11より，$[g,h]$とその共軛を用いることで，エッヂキューブ$e_{1}, e_{2}, e_{3}, e_{4}$は自由に反転できることがわかります（ただし，総反転数が保存する必要はあります）．

基本定理の十分性の証明，或はルービックキューブを交換子（だけ）で揃える方法

前節での考察をもとに基本定理の十分性を証明しましょう．

そこで，拡張ルービック変換$\gamma \in \Gamma_{\mathrm{rubik}}$が

1. $\mathrm{sgn}(p_{V}(\gamma)) = \mathrm{sgn}(p_{E}(\gamma))$;
2. $o_{V}(\gamma)_{1} + \cdots + o_{V}(\gamma)_{8} \equiv 0 \pmod3$;
3. $o_{E}(\gamma)_{1} + \cdots + o_{E}(\gamma)_{12} \equiv 0 \pmod2$

を満たしているとします．このとき，可能配置$I \cdot \gamma$が可解配置であることを示すためには，ルービック変換$g_{\gamma} \in G_{\mathrm{rubik}}$であって$(I \cdot \gamma) \cdot g_{\gamma} = I$となるものが存在することを示せばよいことになります．

定理5の必要性と補題1，補題3より，任意の$g \in G_{\mathrm{rubik}}$に対して$\gamma g \in \Gamma_{\mathrm{rubik}}$も上の3条件を満たすことに注意しましょう．

上の証明において，$g_{2}, g_{3}, g_{4}$は交換子の積で書けることに注意すると，ルービックキューブは交換子だけで揃えられると放言しても許される気がしてきます．実際にやってみろと言われるとそれはまた別の話になりますが．

補遺：ルービックキューブ群の構造

まず，基本定理からただちにつぎがわかります：

拡張ルービックキューブ群$\Gamma_{\mathrm{rubik}}$の部分群$\Gamma_{\mathrm{rubik}}'$をつぎで定めます：
$$ \Gamma_{\mathrm{rubik}}' = \left\{\gamma \in \Gamma_{\mathrm{rubik}} \middle|\ \sum o_{V}(\gamma)_{i} = 0, \sum o_{E}(\gamma)_{j} = 0\right\}. $$
また，$(\mathbb{Z}/3)^{7}$と$\{n \in (\mathbb{Z}/3)^{8} \mid \sum n_{i} = 0\}$，および$(\mathbb{Z}/2)^{11}$と$\{m \in (\mathbb{Z}/2)^{12} \mid \sum m_{j} = 0\}$を自然に同一視します．このとき，次が成り立ちます：

基本定理の系より$G_{\mathrm{rubik}}$は$\Gamma_{\mathrm{rubik}}'$の部分群ですが，より詳しく次が成り立ちます：

最後に，
$$ \Gamma_{\mathrm{rubik}}' \cong_{\mathrm{Grp}} (S_{8} \times S_{12}) \ltimes ((\mathbb{Z}/3)^{7} \times (\mathbb{Z}/2)^{11}) $$
および
$$ \{(\sigma, \tau) \in S_{8} \times S_{12} \mid \mathrm{sgn}(\sigma) = \mathrm{sgn}(\tau)\} = (S_{8} \times S_{12}) \cap A_{20} $$
に注意すると，次がわかります：

更新履歴

2023/08/06：

• ルービックキューブのラベル付けを変更しました．
• 回転数，反転数の定義を修正しました．
• 合せて関係各所の修正・書き換えを行いました．