文献あり

量子コンピュータにおける素因数分解(3): 量子フーリエ変換

はじめに

この記事は量子コンピュータによる素因数分解のアルゴリズムである「Shorのアルゴリズム」の解説記事第3回目です。1,2回目は以下：

第3回は量子フーリエ変換（Quantum Fourier Transform, QFT）に関して書きます。前回導入したべき剰余の計算
\begin{align} \hspace{1.5cm} a^x \text{ mod }N \end{align}
を行う量子回路と共に、Shorのアルゴリズムにおいて中心的な役割を担います。

本記事ではフーリエ変換の基礎知識はあるものとして話を進めます（※深い知識は必要ないです。定義+αくらい知っていれば十分です）。ご了承ください。

本記事はRef.1を参考にしています。

量子フーリエ変換（QFT）とは

以下の変換を行う量子回路を考えます：

\begin{align} \hspace{1.5cm} |j\rangle\to\frac{1}{2^{n/2}}\sum_{k=0}^{2^n-1}\tag{1} \exp(2\pi i j k /2^n)|k\rangle \end{align}

前回までの記事にあるように、$|j\rangle \ (j\text{は}0\le j < 2^n\text{をみたす整数})$とは、$j$を2進数表示した各桁を$j_i\in \{0,1\} \ (i=0,1,2,\cdots,n-1)$として
\begin{align} \hspace{1.5cm} |j\rangle:=|j_0\rangle|j_1\rangle\cdots |j_{n-1}\rangle \end{align}
のことです（2値を取る量子状態$|0\rangle,|1\rangle$の存在は仮定します）。Eq.(1)の変換ができれば、$\sum_{j=0}^{N-1}x_j|j\rangle$という重ね合わせの状態にこれを施すことで
\begin{align} \hspace{1.5cm} \sum_{j=0}^{N-1}x_j|j\rangle\to \sum_{k=0}^{N-1}y_k|k\rangle, \ \ \ \ y_k=\frac{1}{\sqrt{N}}\sum_{l=0}^{N-1}\exp(2\pi i k l/N)x_l, \ \ N=2^n \end{align}
を得ます。このようにして$x_j$の離散フーリエ変換$y_j$の情報を持つ状態を作ることができます。ただし実際に量子状態を観測して$y_j$を得るのは現実的でないことに注意してください（Ref.Nielsen P220）。この観測はQFTの速さを無意味にするほど時間がかかります。QFTの量子回路は、あくまで他のアルゴリズム（今回はShorのアルゴリズム）の部品、サブルーチンとして使うものです。

以下Eq.(1)を実現する量子回路、すなわちQFTの量子回路を構成します。

QFTを実現する量子回路の構成

QFTの量子回路において次が成立することが重要です：
\begin{align} \hspace{1.5cm} \frac{1}{2^{n/2}}\sum_{k=0}^{2^n-1}e^{2\pi i j k/2^n}|k\rangle &=\frac{1}{2^{n/2}} \sum_{k_0=0}^1 \sum_{k_1=0}^1 \cdots \sum_{k_{n-1}=0}^1 e^{2\pi i j (\sum_{l=1}^n k_{l-1}/ 2^{l})}|k_0\rangle|k_1\rangle\cdots |k_{n-1}\rangle\\ &=\frac{1}{2^{n/2}}\left(\sum_{k_0=0}^1e^{2\pi i j k_0/2^1}|k_0\rangle\right) \left(\sum_{k_1=0}^1e^{2\pi i j k_1/2^2}|k_1\rangle\right) \cdots \left(\sum_{k_{n-1}=0}^1e^{2\pi i j k_{n-1}/2^n}|k_{n-1}\rangle\right)\\ &=\frac{1}{2^{n/2}}(|0\rangle+e^{{2\pi i j/2^1}}|1\rangle) (|0\rangle+e^{{2\pi i j/2^2}}|1\rangle) \cdots (|0\rangle+e^{{2\pi i j/2^n}}|1\rangle)\tag{2} \end{align}
最初の行では$k=k_02^{n-1}+k_1 2^{n-2}+\cdots + k_{n-1}2^0$としています。

ここで$j$を$j=j_02^{n-1}+j_1 2^{n-2}+\cdots + j_{n-1}2^0$のように2進数表示します。Eq.(1)の各括弧内の位相ファクター$\exp(2\pi i(j/2^l))$において、$j/2^l$の整数部分は無視できます。ゆえに$\exp$の肩は
\begin{align} \hspace{1.5cm} &j/2^1\to j_{n-1}/2^1\\ &j/2^2\to j_{n-2}/2^1+j_{n-1}/2^2\\ &\vdots\\ &j/2^n\to j_{0}/2^1+j_1/2^2+\cdots+j_{n-1}/2^n \end{align}
としてよいです。よって
\begin{align} \hspace{1.5cm} \text{Eq.(2)}=\frac{1}{2^{n/2}}(|0\rangle+e^{{2\pi i (j_{n-1}/2^1)}}|1\rangle) (|0\rangle+e^{2\pi i (j_{n-2}/2^1+j_{n-1}/2^2)}|1\rangle) \cdots (|0\rangle+e^{2\pi i (j_{0}/2^1+j_1/2^2+\cdots+j_{n-1}/2^n)}|1\rangle)\tag{3} \end{align}
となります。よって初期状態として
\begin{align} \hspace{1.5cm} |j\rangle=|j_0\rangle|j_1\rangle\cdots|j_{n-1}\rangle \end{align}
を用意し、この各qubitをEq.(3)のように変換する量子回路を組めばフーリエ変換ができたことになります。

ここで「小数バイナリ表示」を導入します:

小数バイナリ表示

\begin{align} \hspace{1.5cm}j_0/2^1+j_1/2^2+\cdots+j_{n-1}/2^n \text{ を } 0.j_0j_1\cdots j_{n-1}\text{ のように表す} \end{align}

するとEq.(3)は
\begin{align} \hspace{1.5cm} \text{Eq.(3)} = \frac{1}{2^{n/2}} (|0\rangle+e^{2\pi i \ 0.j_{n-1}}|1\rangle) (|0\rangle+e^{2\pi i \ 0.j_{n-2}j_{n-1}}|1\rangle) \cdots (|0\rangle+e^{2\pi i \ 0.j_0j_1\cdots j_{n-1}}|1\rangle)\tag{4} \end{align}
と書けます。文献ではこの形で書くことが多いです。

Eq.(4)を実現するのに以下の2つの量子ゲートを導入します：

QFTに必要な量子ゲート

アダマール（Hadamard）ゲート:
これは1 qubitに作用するゲートであり、以下の変換を行う
\begin{align} \hspace{1.5cm} |0\rangle\mapsto \frac{|0\rangle+|1\rangle}{\sqrt{2}}, \ \ \ |1\rangle\mapsto \frac{|0\rangle-|1\rangle}{\sqrt{2}} \end{align}
このゲートを$\hat H^{(i)}$で表す。$i$はHadamrdゲートが作用するqubitの番号。量子回路図では以下のように表す：
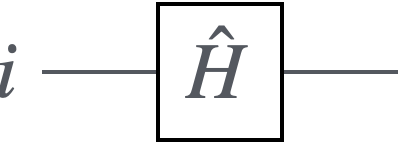Hadamardゲートの量子回路図
制御$\boldsymbol{R_k}$（controlled-$\boldsymbol{R_k}$）ゲート:
2 qubitに作用するゲート。1つはcontrol qubit, もうひとつがtarget qubit。control qubitが$|1\rangle$のとき、target qubitの$|1\rangle$に$e^{2\pi i/2^k}$の位相をかける。このゲートを$\hat R_k^{(lm)}$で表す。ここで$l$はcontrol qubitの番号、$m$はtarget qubitの番号。量子回路図では$R^{(lm)}_k$を以下のように表す：
$\hat R_k^{(lm)}$の量子回路図

これらのゲートを用いてQFTの量子回路を作ります。ゲートの定義より\begin{align} \hspace{1.5cm} &\hat H^{(i)}(\alpha|0\rangle_i+\beta|1\rangle_i) =\frac{1}{\sqrt{2}}(\alpha+\beta)|0\rangle_i +\frac{1}{\sqrt{2}}(\alpha-\beta)|1\rangle_i,\\ &\hat R_k^{(lm)}|j_l\rangle(\alpha|0\rangle_m+\beta|1\rangle_m) =|j_l\rangle(\alpha |0\rangle_m+e^{2\pi i j_l/2^k}\beta|1\rangle_m) \end{align}
が成立します。最初の式より$\hat H^{(i)}|j_i\rangle, \ j_i\in \{0,1\}$は以下のようにかけることがわかります：
\begin{align} \hspace{1.5cm} \hat H^{(i)}|j_i\rangle&=\frac{1}{\sqrt{2}}(|0\rangle_i+e^{\pi i j_i}|1\rangle_i)\\ &=\frac{1}{\sqrt{2}}(|0\rangle+e^{2\pi i j_i/2^1}|1\rangle)\\ &=\frac{1}{\sqrt{2}}(|0\rangle+e^{2\pi i \ 0.j_i}|1\rangle) \end{align}
これらの式から以下が成立します：
\begin{align} \hspace{1.5cm} \hat H^{(0)} |j_0\rangle&=\frac{1}{2^{1/2}}(|0\rangle+e^{2\pi i \ 0.j_0}|1\rangle),\\ \hat R_2^{(1\ 0)}\hat H^{(0)}|j_0\rangle|j_1\rangle&= \frac{1}{2^{1/2}}(|0\rangle+e^{2\pi i\ 0.j_0j_1}|1\rangle)|j_1\rangle,\\ \hat R_3^{(2\ 0)}R_2^{(1\ 0)}\hat H^{(0)}|j_0\rangle|j_1\rangle|j_2\rangle&= \frac{1}{2^{1/2}}(|0\rangle+e^{2\pi i \ 0.j_0j_1j_2}|1\rangle)|j_1\rangle|j_2\rangle,\\ \vdots \end{align}
一般化すると以下が成立することがわかります：

\begin{align} \hspace{1.5cm} &R_k^{(i+k \ i)}R_{k-1}^{(i+k-1\ i)} \cdots R_2^{(i+1\ i)} \hat H^{(i)} |j_0\rangle|j_1\rangle\cdots|j_{i-1}\rangle|j_i\rangle|j_{i+1}\rangle\cdots|j_{i+k}\rangle\\ &=(|j_0\rangle |j_1\rangle\cdots |j_{i-1}\rangle) \frac{1}{2^{1/2}} (|0\rangle_i +e^{2\pi i\ 0.j_ij_{i+1}\cdots j_{i+k}}|1\rangle_i) |j_{i+1}\rangle|j_{i+2}\rangle\cdots|j_{i+k}\rangle \end{align}

ここで$\hat K(i;k)$を以下のように定義します：
\begin{align} \hspace{1.5cm} \hat K(i;k):=\hat R_k^{(i+k-1\ i)}\hat R_{k-1}^{(i+k-2\ i)}\cdots R_2^{(i+1 \ i)} \hat H^{(i)} \end{align}
すると
\begin{align} \hspace{1.5cm}\text{Eq.(4)}=\hat H^{(n-1)}\hat K(n-2;2)\cdots\hat K(1;n-1) \hat K(0;n)|j_0\rangle|j_1\rangle\cdots|j_{n-1}\rangle\tag{5} \end{align}
と書けます。

Eq.(5)を図にすると図3のようになります：
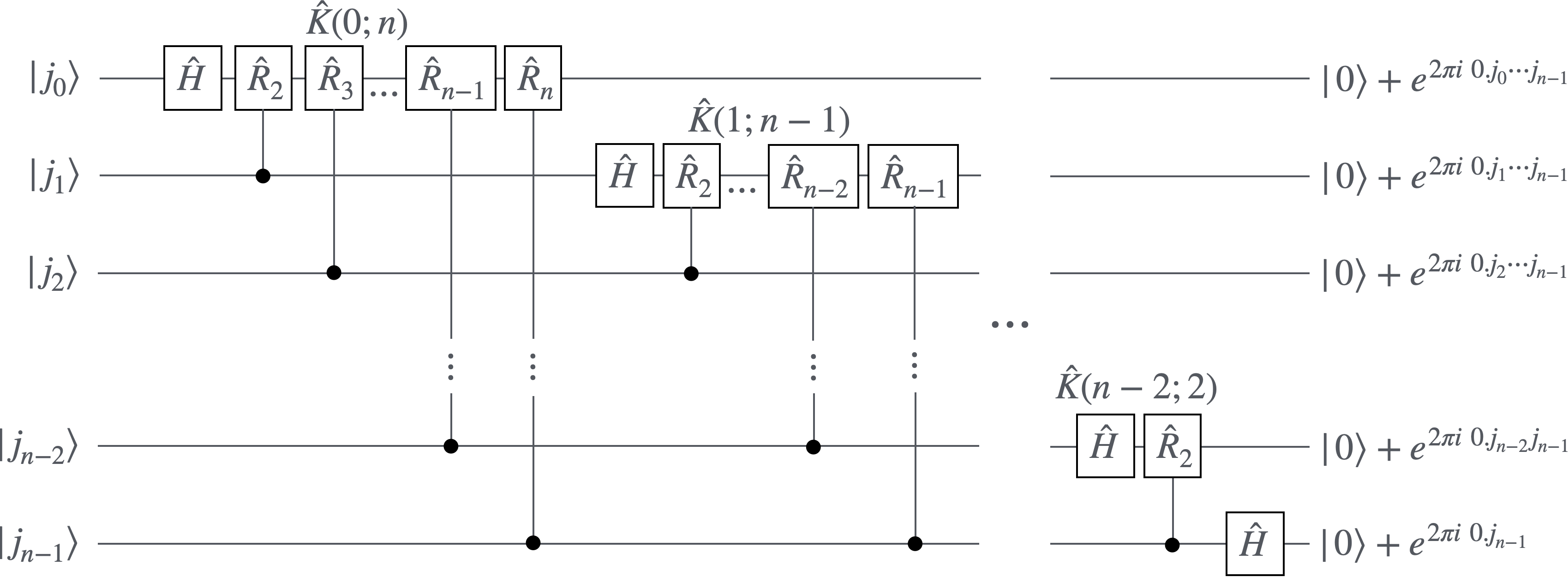フーリエ変換を実現する量子回路図