曲線の長さはどこで測られているか？

概要

普通の Euclid 空間で曲線の長さを測る時、特に深く意識はしないことだが、もうちょっと高尚に多様体目線で見た時には、どこで長さが測られていると思えるのか気になったので少しまとめてみたい。

簡単な例 1

平面の中の原点$(0,0) \in \mathbb{R}^{2}$から点$(x,y) \in \mathbb{R}^{2}$への距離を測りたい時、いわゆるピタゴラスの定理により、長さは$(x^{2}+y^{2})^{1/2}$となるであろう。この$(x, y)$が原点に限りなく近い時、これを$(\Delta x, \Delta y)$とでも書くことにすると長さは$((\Delta x)^{2} + (\Delta y)^{2})$になるだろう。
覚えていないが、たぶん中学の数学の範囲だったと思う。

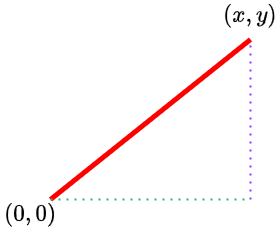ピタゴラスの定理

簡単な例 2

次に平面の中の適当に滑らかな曲線$\gamma(\cdot) \in \mathbb{R}^{2}$について考えてみたい。$t \in [0,1]$というパラメータを用いて

$$ \begin{align*} \gamma(t)=(x(t), y(t)) \end{align*} $$

と書かれているとする。$\gamma(0)$が始点$P$で、$\gamma(1)$が終点$Q$とする。長さを測るためには素朴に折れ線近似を考えよう。

十分に大きな$n \in \mathbb{N}$をとって、$t_{i}=\frac{i}{n}$として$P = \gamma(0)$, $Q = \gamma(1)$となるような点列$P=P_{0}, P_{1}, ..., P_{n}=Q$を考える。この点列を結ぶ線分の長さを考えると、これは$n$本の線分の長さの和になる。$i=0, 1, ...,n−1$に対して、$P_{i}$と$P_{i+1}$を結ぶ線分の長さは$((x(\frac{i+1}{n})−x(\frac{i}{n}))^{2}+(y(\frac{i+1}{n})−y(\frac{i}{n}))^{2})^{1/2}$である。これを$n$本の線分について足し合わせると、$n$本の線分の長さの和が得られる。$n$を無限大に近づけると、この和は$\gamma$の長さに収束するだろう。（と、Copilot が勝手に文章を書いてくれたが、悪くなさそうなのでそのまま採用した）

この線分の長さの総和は$\Delta x_{i}=x(\frac{i+1}{n})−x(\frac{i}{n})$, $\Delta y_{i}=y(\frac{i+1}{n})−y(\frac{i}{n})$,$\Delta t=\frac{1}{n}$と書くことにすると、

$$ \begin{align*} &\sum_{i=0}^{n−1}(\Delta x_{i}^{2}+\Delta y_{i}^{2})^{1/2} \\ =&\sum_{i=0}^{n−1}\left(\left(\frac{\Delta x_{i}}{\Delta t}\right)^{2}+\left(\frac{\Delta y_{i}}{\Delta t}\right)^{2}\right)^{1/2} \Delta t \\ \to &\int_{0}^{1}(x'(t)^{2}+y'(t)^{2})^{1/2} dt \end{align*} $$

となって、ピタゴラスの定理に極小の距離の和が積分の形になる。たぶん高校の数学の範囲だったと思う。この極限値を曲線$\gamma$の長さ$L$と呼んだであろう。

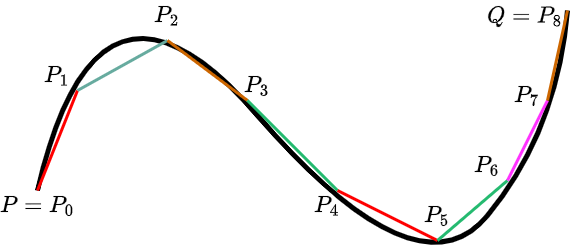折れ線近似

さて、$\gamma'(t)=(x'(t), y'(t))$と書くことにすると、ちょっとカッコをつけて

$$ \begin{align*} L = \int_{0}^{1} \|\gamma'(t)\| dt \end{align*} $$

となる。ここで$\|\cdot\|$は気取って書くと Euclid ノルムというやつになる。

無限小のベクトルはどこにいる？

ここで、$\gamma'$はどこにいるのか？ ということについて考えたい。

結局、オチとしては「接空間にいるので～」ということになって以下は大変つまらない内容である。ただ、普通にはどう考えても平面上の無限小のベクトルでしょとしか思えないが、一方で無限小のベクトルは厳密には書けないので、書けない以上は普通には存在していないとも言えるわけではある。

突如多様体$M$について考えよう。多様体は位相空間であって、局所的に Euclid 空間と同相であるようなものであった。Möbius の帯のようなものを考えると、局所的には 2 次元平面だが、全体としては「うむむ？」という形状なので、全体としては Euclid 空間には一致しない。

という定理があるようで（ Ref. [1] 定理 13.13）、これを考えると大体の多様体は Euclid 空間の図形のような気もするし、Möbius の帯も紙工作できることから分かるように、3 次元空間、特に$\mathbb{R}^{2×2+1} = \mathbb{R}^{5}$に埋め込めている。

とは言え、性質の良い場合の話なので、何でもかんでも Euclid 空間の中で考えるのも宜しくない（よく分からないという場合もあるだろうし）。ということで、多様体論は多様体の中で考えるのが基本であるだろう。

接空間

多様体の接空間という概念がある。多様体$M$の点$p \in M$に対して、$p$に “接する” ベクトルの集合を$T_{p}M$と書く。これは$p$に接するベクトルの集合である。多様体$M$が$m$次元であるとすると、$T_{p}M$は$p$に “接する” $m$次元のベクトル空間になる。$T_{p}M$の元を接ベクトルと呼ぶ。（と、再び Copilot が勝手に文章を書いてくれたが、悪くなさそうなのでそのまま採用した）

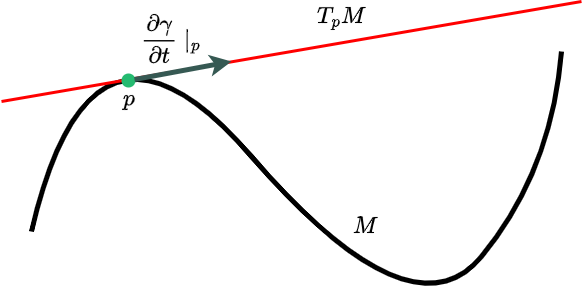接空間

先の曲線を 1 次元多様体と思うと、典型的には赤線のようなものを「接空間」のイメージ図とするのであろうが、あまりこのイメージが良くないこともあるし、「接束」を考える時に絵的にイマイチだと思うが、「長さ」の話をする時はこれでも良さそうなので、これにしておく。

さて、この曲線を多様体と思いたい。記号を流用して

$$ \begin{align*} M: [0,1] \simeq \gamma \ (\subset \mathbb{R}^{2}) \end{align*} $$

でほぼほぼ自明な局所座標が入った多様体と考えられるだろう。素朴な曲線論のイメージを可視化したような図にしたが、この図からしても接ベクトルは多様体$M$の外にいってしまっていて、接空間$T_{p}M$に入っていそうである。曲線論の話を思い出すとこの接ベクトルを無限小の長さにした時に、その長さを測りたい。それを各点$p \in M$で足し合わせると、多様体上の曲線の長さも測れるのではないかということになるだろう。

計量テンソル

突然難しそうなキーワードが出て来る。曲線の長さを測りたいというお話だったので、実は今まで考えていた多様体$M$は Riemann 多様体で、Riemann 計量というものが入っていますと思うことにする。Riemann 計量とは接空間$T_{p}M$の 内積 である。ベクトル空間のベクトルの長さを測るなら内積だということである。$p \in M$ごとに$T_{p}M$に定まるこの内積$g_{p}$は

$$ \begin{align*} g_{p}:T_{p}M×T_{p}M→\mathbb{R} \end{align*} $$

という双線型写像であるが、多重線型代数の用語を用いてちょっとカッコイイ書き方をすると、

$$ \begin{align*} [T_{p}M×T_{p}M→\mathbb{R}]=(T_{p}M×T_{p}M)^{∗}≃T_{p}M^{∗} \otimes T_{p}M^{∗} \end{align*} $$

となってしまい、「$g_{p} \in T_{p}M^{∗} \otimes T_{p}M^{∗}$なので、2 階共変テンソルですね」みたいなとんでもないことになってしまう。が、居場所を「近所の宿泊施設」と呼ぶか「ホテルニューグランド」と呼ぶかの違いくらいだと思う。2 階共変テンソルとかどうでも良くて、単に内積である。$g_{p}$を内積らしくするために$\langle \cdot, \cdot \rangle_{p}$と書くことにすると、$\xi \in T_{p}M$に対してノルム

$$ \begin{align*} \|\xi\|_{p}=(\langle \xi, \xi \rangle_{p})^{1/2} \end{align*} $$

を導入できる。後は、何かしらの形で積分が定まれば多様体上の曲線の長さを測ることができるだろう。

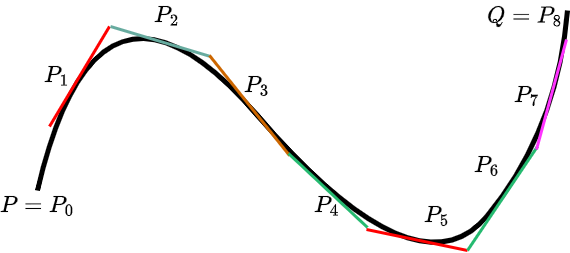無限小の接ベクトルの長さを測る

と言うことで、曲線を外側の空間を使って折れ線近似をして長さを測っているつもりが、気が付いたら接空間の中でベクトルの長さを測っていたのである。

故郷の Euclid 空間に帰ってくる

多様体の話になったので何か特別な話をしている感じがするが、Euclid 空間もまた多様体として考えられるので、ここまでの話はすべて Euclid 空間にも適用できる。ではこの観点で見るとどうなるか？

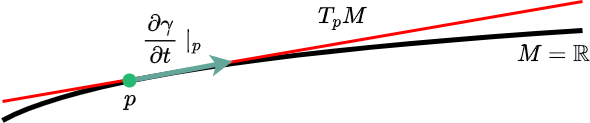Euclid 空間における曲線の長さ

少し見やすくするために$M=\mathbb{R}$を曲げているが、Euclid 空間の各点で自身と見分けのつかない空間が接空間としてべたっと貼りついていると考えることができるのである。実は我々は Euclid 空間の中で曲線の長さを測っていると思っていたら、いつの間にか 透明なフィルムのように貼りついた平らな接空間の上で無限小のベクトルの長さを測って足し合わせていた というのである。

まとめ

この記事はただの冗談である。途中で触れた「Whitney の埋め込み定理」によって、普通のシチュエーションならちょっと次元は高まるが Euclid 空間の中の図形として具現化されているはずである。なので、素直に多様体の外の領域を活用して折れ線近似で長さを測っていると思えば良いのではないだろうか。

あと、ここでも Copilot が総括してくれたが、そのお気持ちは狙いとちょっと違ったので棄却して、自分で書いた。