距離空間5 中点

前回は内在的距離の具体例をみました.距離 $d$ は曲線の長さによる長さ構造 $L_{d}$ を誘導し,その長さ構造から内在的距離 $d_{L_{d}}$ が定まるのでした.そうして距離空間 $(X, d)$ から誘導された内在的距離空間 $(X, \hat{d})$ の自然な構成を得ました.
では,内在的距離ではないものにはどんなものがあるのでしょうか.距離が内在的であるための条件については後で詳しくみていきますが,一つ例を挙げようと思います.

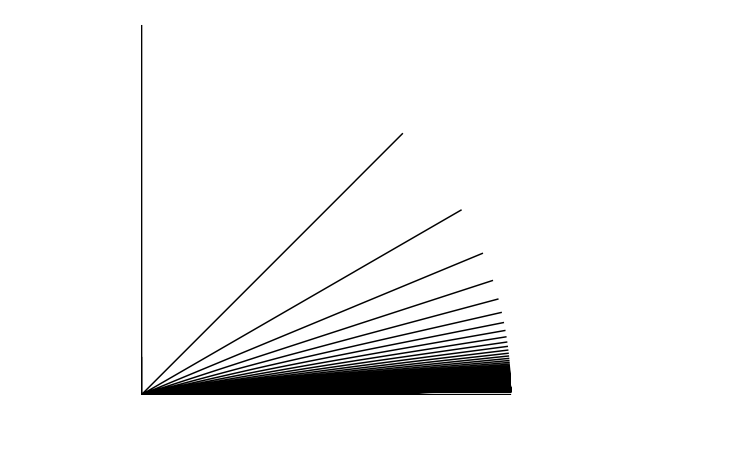
$R^{2}$ の部分空間 $⋃_{i = 1}^{\infty} [(0, 0), (\cos \frac{1}{i}, \sin \frac{1}{i})] \cup [(0, 0), (1, 0)]$ を考える.ただし $[a, b]$ で点 $a, b$ を結ぶ線分を表す.この位相空間は長さ空間と同相にならない.
a

相対位相で ${(\cos \frac{1}{i}, \sin \frac{1}{i})}_{i}$ は $(1, 0)$ に収束する.長さ空間におけるこれらの点の距離は常に $2$ 以上なので矛盾する. $◻$

これは長さ空間の部分空間が長さ空間になるとは限らない例であり,内在的距離による位相が元の空間の位相と異なる例でもあります.じゃあいつなるのか？ということは置いておいて~~今でしょ！~~より一般に次のことが成り立ちます.

長さ空間 $X$ は局所道連結,すなわち,任意の点の任意の近傍は道連結な近傍を含む.

$x \in X$ とし $U_{x}$ を $x$ の近傍とする.ある $0 < r < \infty$ であって $B (x, r) \subseteq U_{x}$ なるものが存在する.もし開球 $B (x, r)$ のある点と $x$ を結ぶ道が存在しなければ距離は $\infty$ となり矛盾する. $◻$

さて,前回は距離から内在的距離を得る方法を考えましたがこの方法で次々と新しい距離空間を得ることができるのでしょうか.

$(X, d)$ を距離空間, $\hat{d}$ を $d$ から誘導される内在的距離とする.
(1) $γ$ が $(X, d)$ で有限長なら $L_{\hat{d}} (γ) = L_{d} (γ)$
(2) $\hat{d}$ に誘導された内在的距離は $\hat{d}$ に一致する.

一般化三角不等式から道の長さの方が大きいので $\hat{d} \geq d$ .これより $L_{\hat{d}} (γ) \geq L_{d} (γ)$ .逆の不等号を示すため $γ : [a, b] \to X$ を道, $Y = {y_{j}}$ を $[a, b]$ の分割とする.左辺は右辺の形で表される道の長さ全体の下界だから $\hat{d} (γ (y_{j}), γ (y_{j + 1})) \leq L_{d} (γ, y_{j}, y_{j + 1})$ .よって
$\sum_{\hat{d}} (Y) = \sum d (γ (y_{i}), γ (y_{i + 1})) \leq L_{d} (γ)$ . $Y$ は任意だから $L_{\hat{d}} (Y) \leq L_{d} (γ)$ となる.
(1)から明らか. $◻$

異なる長さ構造が同じ内在的距離を誘導することがあります.どのような長さ構造が内在的距離に誘導されたものでしょうか.

$L$ が下半連続な長さ構造なら, $L$ は内在的距離 $d = d_{L}$ に誘導された長さ構造に一致し, $L$ のすべての認容的道 $γ$ に対し $L (γ) = L_{d} (γ)$

$L_{d} (γ) \leq L (γ)$ は常に成立する. $γ : [a, b] \to X$ を有限長な道とすると, $L$ の連続依存性により関数 $L (t) = L (γ |_{[a, t]})$ は $[a, b]$ 上一様連続である.よって任意の $ϵ > 0$ に対してある分割 $a = t_{0} \leq t_{1} \leq \dots \leq t_{k + 1} = b$ であって任意の $i$ に対して $d_{L} (γ (t_{i}), γ (t_{i + 1})) < ϵ$ を満たすものが存在する. $d_{L}$ の定義から $γ (t_{i})$ から $γ (t_{i + 1})$ への道 $σ_{i}$ であって $L (σ_{i}) \leq d_{L} (γ (t_{i}), γ (t_{i + 1})) + \frac{ϵ}{k + 1}$ を満たすものが存在する. $σ_{i}$ たちの積 $h_{ϵ}$ に対して
$L (h_{ϵ}) = \sum_{i = 0}^{k} L (σ_{i}) \leq \sum_{i = 0}^{k} d_{L} (γ (t_{i}), γ (t_{i + 1})) + ϵ \leq L_{d} (γ) + ϵ$ .三角不等式から任意の $t$ に対して $d_{L} (γ (t), h_{ϵ} (t)) \leq 3 ϵ$ .
(実際,一様連続性からある $i$ が存在して $d_{L} (γ (t), γ (t_{i + 1})) < ϵ$ が成り立つ.示した不等式と同様に
$d_{L} (h_{ϵ} (t), h_{ϵ} (t_{i + 1})) \leq L (h_{ϵ} |_{[t, t_{i + 1}]}) \leq L_{d} (γ |_{[t, t_{i + 1}]}) + ϵ \leq d (γ (t_{i}), γ_{t_{i + 1}}) + ϵ < 2 ϵ$ .よって
$d_{L} (γ (t), γ (t_{i + 1})) \leq d_{L} (γ (t), γ (t_{i + 1})) + d_{L} (h_{ϵ} (t), h_{ϵ} (t_{i + 1})) < 3 ϵ$ )
よって $h_{ϵ} (t) \to γ (t)$ が $d$ による位相が元の位相より細かい(これは $L$ の条件 $4$ による)ことからわかる. $L$ の下半連続性から
$L (γ) \leq \underset{ϵ \to 0}{lim inf} L (h_{ϵ}) \leq L_{d} (γ)$ . $◻$

もし距離が内在的であれば,そこからさらに長さ構造の構成を経て内在的距離を構成しても最初と同じ距離が得られることがわかりました.内在的距離の性質をみていきましょう.意外と重要になるのが中点の存在です.

中点,

ϵ -

中点

距離空間 $(X, d)$ の点 $z \in X$ は $x, y \in X$ に対し $d (x, z) = d (z, y) = \frac{1}{2} d (x, y)$ を満たすとき $x$ と $y$ の中点であるという.
また, $| 2 d (x, z) - d (x, y) | \leq ϵ$ , $| 2 d (z, y) - d (x, y) | \leq ϵ$ を満たすとき $ϵ -$ 中点という.

距離空間 $(X, d)$ の距離 $d$ が狭義内在的であるとすると,任意の $x, y \in X$ に対し,中点 $z$ が存在する.

$d$ は狭義内在的だから $x$ から $y$ への最短の道 $γ : [a, b] \to X$ の長さは $L (γ) = d (x, y)$ である. $L (t) = L (γ |_{[a, t]})$ とおく. $L (t)$ は連続, $L (0) = 0$ だから中間値の定理によりある $c \in [a, b]$ が存在して $L (c) = \frac{1}{2} L (b)$ を満たす.今, $z = γ (c)$ とすると $d (x, z) \geq \frac{1}{2} L (b)$ , $d (y, z) \geq \frac{1}{2} L (b)$ なので三角不等式から $d (x, z) = d (y, z) = \frac{1}{2} L (b)$ . $◻$

狭義とは限らない場合も任意の $ϵ > 0$ の誤差を除いた結果が成り立ちます.

$d$ を内在的距離とし $ϵ > 0$ とする.任意の $x, y \in X$ に対し $ϵ -$ 中点が存在する.

$γ$ を $L (γ) - d (x, y) \leq ϵ$ を満たす道とすれば同様の主張がいえる.
(実際上と同様の記号で三角不等式により
$0 \leq L (c) - d (x, γ (c)) + L (c) - d (γ (c), y) \leq L (γ) - d (x, y) < ϵ$ .特に
$| L (c) - d (x, γ (c)) | < ϵ$ , $| \frac{1}{2} L (γ) - \frac{1}{2} d (x, y) | < \frac{ϵ}{2}$ なので
$| d (x, γ (c)) - \frac{1}{2} d (x, y) | < \frac{3 ϵ}{2}$ となり $| 2 d (x, γ (c) - d (x, y)) | < 3 ϵ$ を得る.)

中点をとる操作を繰り返すことにより次の系は明らかです.

補題5

$X$ を狭義内在的距離 $d$ を備えた空間とする.任意の $ϵ > 0$ と任意の $x, y \in X$ に対し,ある有限列 $x_{1} = x, x_{2}, \dots, x_{k} = y$ であって任意の $i \in {1, 2, \dots, k - 1}$ に対して $d (x_{i}, x_{i + 1}) \leq ϵ$ かつ $\sum_{i = 1}^{k - 1} d (x_{i}, x_{i + 1}) = d (x, y)$ を満たすものが存在する.

内在的距離については最後の式を $\sum_{i = 1}^{k - 1} d (x_{i}, x_{i + 1}) - d (x, y) \leq ϵ$ に置き換えたものが成り立ちます.

投稿日：2月5日

更新日：2月10日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

qq_pp

3794

他の人のコメント

コメントはありません。

読み込み中

qq_pp

距離空間5 中点