文献あり

アポロニウスの円と二点を通る円とその間の曲線

144

はじめに

こんにちは、AAGです。
今日は研究中に偶然生まれた不思議な曲線について語りたいと思います。
後で知ったことによる双極座標系というもので考えるのもいいっぽいです。

アポロニウスの円

アポロニウスの円をご存じでしょうか？
ある二点からの距離の比が等しい点の集まりが円になるので、そうやって作った円のことをアポロニウスの円といいます。
3:1のアポロニウスの円
これは、基準となった二点を通る任意の円と直交するのですが、これらの証明は読者に任せます。（反転とか使えるかも）
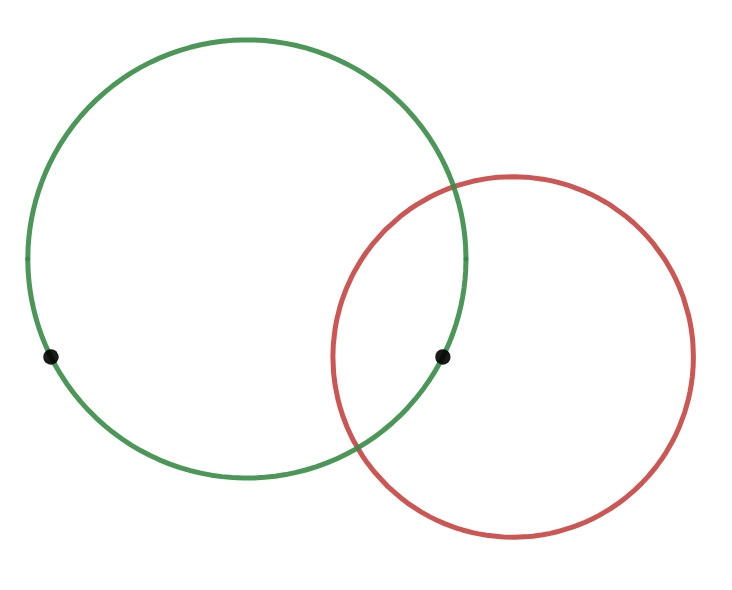直交

二点を通る円

有向角というものを導入すれば
「二点$A,B$に対して$\measuredangle APB$が等しい点$P$の集まり（および$A,B$自身）」
といえます。
くわしくはこちらを参照

対数螺旋のようなもの

今回紹介するのは以下の図のような曲線群です。
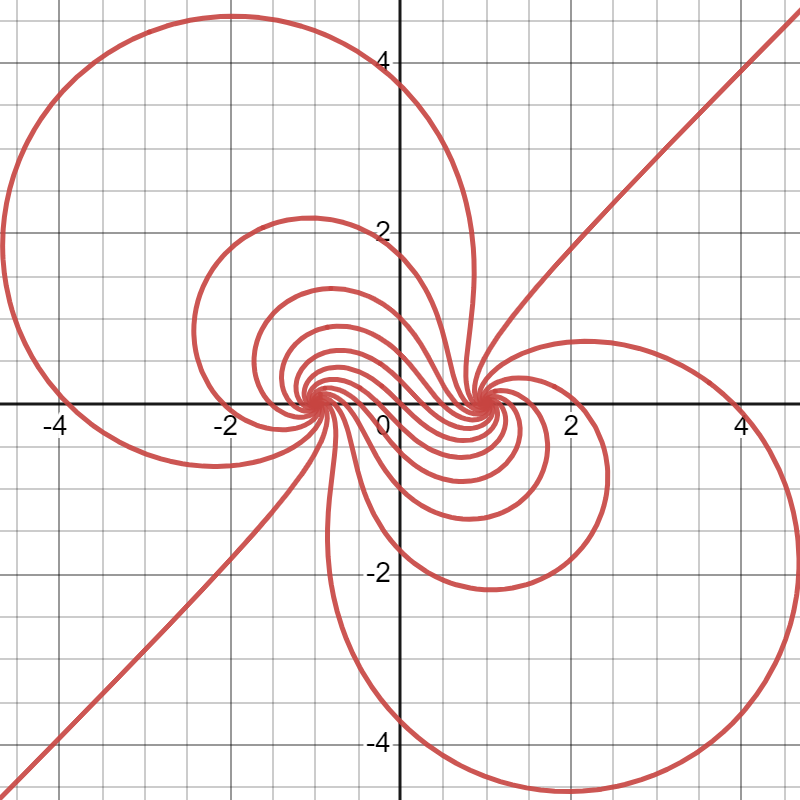なんと説明すればいいのかわからん
各々ある二点$A,B$からの「距離の比」と「$e^{\measuredangle APB}$」の比が一定になるような点$P$の集まりになっています。
（もしかしたら逆比になっているかもしれません）
$e^{\measuredangle APB}$の指数を定数倍すれば滑らかに「アポロニウスの円と二点を通る円と」の間を変化します

desmos （bは分子、cは分母だと思ってください）

動機

※微分方程式とちょっとの複素関数の知識を含みます。
複素関数（二次関数）をベクトル場で表したものを曲線で表したくて、
$\dot{z}=(1+i)(z^2+1)$を解いてみたい
$z=r_1e^{i\theta_1}-i=r_2e^{i\theta_2}+i$（$r_1,r_2,\theta_1,\theta_2$は実数値）とおく
\begin{eqnarray} \left\{ \begin{array}{l} \dot{r_1}+ri\dot{\theta_1}=r_1(r_1e^{i\theta_1}-2i)(1+i) \\ \dot{r_2}+ri\dot{\theta_2}=r_2(r_2e^{i\theta_2}+2i)(1+i)\\ \end{array} \right. \end{eqnarray}

\begin{eqnarray} \left\{ \begin{array}{l} \dot{r_1}=r_1^2(\cos(\theta_1)-\sin(\theta_1))+2r_1 \\ \dot{\theta_1}=r_1(\cos(\theta_1)+\sin(\theta_1))-2 \\ \dot{r_2}=r_2^2(\cos(\theta_2)-\sin(\theta_2))-2r_2 \\ \dot{\theta_2}=r_2(\cos(\theta_2)+\sin(\theta_2))+2 \\ \end{array} \right. \end{eqnarray}
$$\frac{\dot{r_1}}{r_1}-\frac{\dot{r_2}}{r_2}$$
$$=r_1(\cos(\theta_1)-\sin(\theta_1))+2-r_2(\cos(\theta_2)-\sin(\theta_2))+2 $$
$$=\mathfrak{Re}(z+i)-\mathfrak{Im}(z+i)+2-\mathfrak{Re}(z-i)+\mathfrak{Im}(z-i)+2$$
$$=2$$
$$\dot{\theta_1}-\dot{\theta_2}$$
$$=r_1(\cos(\theta_1)+\sin(\theta_1))-2-r_2(\cos(\theta_2)+\sin(\theta_2))-2 $$
$$=\mathfrak{Re}(z+i)+\mathfrak{Im}(z+i)-2-\mathfrak{Re}(z-i)-\mathfrak{Im}(z-i)-2$$
$$=-2$$
$$\therefore \frac{\dot{r_1}}{r_1}-\frac{\dot{r_2}}{r_2}=\dot{\theta_2}-\dot{\theta_1}$$
$$\therefore \log {r_1}-\log{r_2}=\theta_2-\theta_1+C'$$
$$\therefore \frac{r_1}{r_2}=Ce^{\theta_2-\theta_1}$$
なんかでてきた