文献あり

三色ネックレスとSchröder路

長さ $ℓ$ のネックレスとは，合計 $ℓ$ 個の何種類かの玉を円形に配置した組合せ論的オブジェクトである [8,4,2,3]．
二つのネックレスは，一方が他方を円に沿って回転して得られるならば，同値であるという．
いわゆる数珠ではないので反転は考えない．すべての玉を区別するネックレスは円順列 [1]という名で有名だが，ここでは区別できない玉もある場合を扱う．

ネックレスとカタラン数

以下が成り立つ [5,6,7]．

玉0を $n$ 個，玉1を $n + 1$ 個使って作る同値でないネックレスの数は， $n$ 番目のカタラン数つまり $\frac{1}{2 n + 1} (\binom{2 n + 1}{n, n + 1}) = \frac{1}{n + 1} (\binom{2 n}{n})$ 通りである．

例えば，3個の0と4個の1でネックレスを作る方法は下図のとおり5通りあり，これは3番目のカタラン数である．
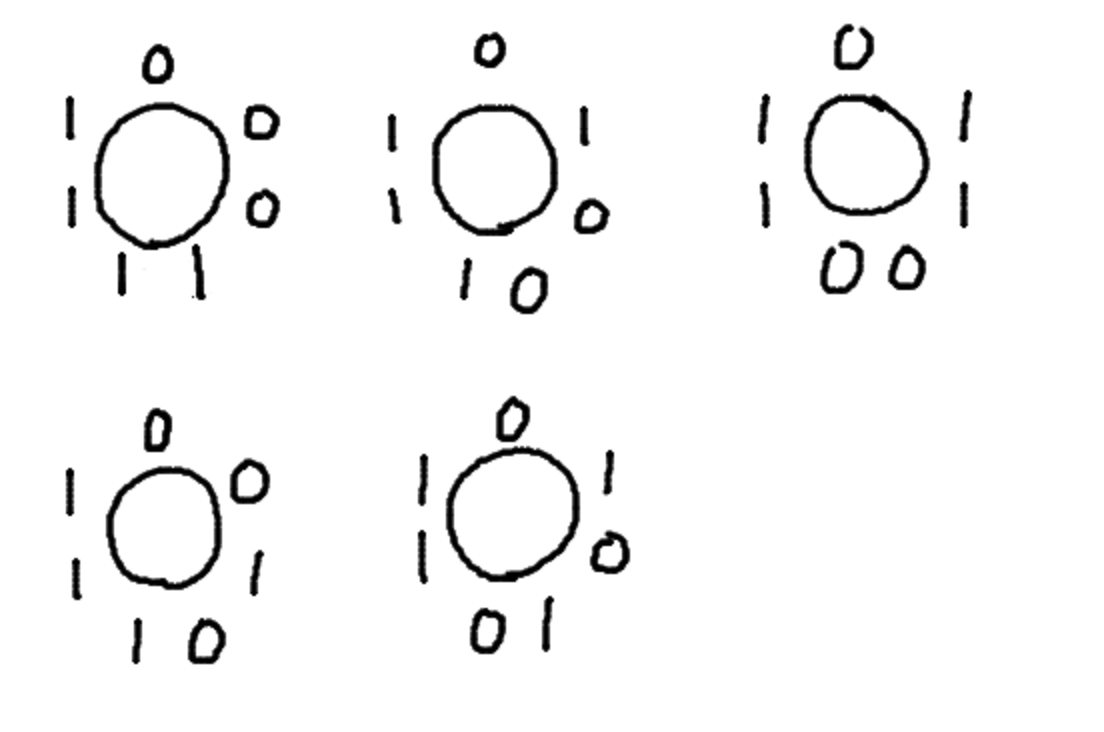3個の0と4個の1でできるネックレス

定理1の代数的証明はBurnsideの補題やPólyaの計数定理 [8,9]を使ってできる．

我々が興味を持つのは，定理1自体よりもむしろ定理1から提起される「全単射を作れ」タイプの問題である．カタラン数はDyck路の数なので，以下の問題が提起される．

「玉0を $n$ 個，玉1を $n + 1$ 個使って作るネックレス」と，「サイズ $n$ のDyck路」の一対一対応を作れ．

問題1の全単射はcycle lemmaと呼ばれる定理を使うとできる．
これについて，例えば[6]や[7]にも書いてあるが，あとで軽く述べる．

三色ネックレスとSchröder路

本記事で述べたいのは，玉を三種類に拡張した場合である．
同じくPólyaの計数定理を使って，以下の主張は簡単に示せる．

玉0を $n$ 個，玉1を $n + 1$ 個，玉2を $n + 2$ 個使って作れる同値でないネックレスの数は $\frac{1}{3 n + 3} (\binom{3 n + 3}{n, n + 1, n + 2})$ 通りである．

ここに現れる数 $\frac{1}{3 n + 3} (\binom{3 n + 3}{n, n + 1, n + 2})$ は，オンライン数列大百科 [10]を見ると

「ピークを $n$ 個持つサイズ $2 n + 1$ のSchröder路の数」（oeis: A319578）

として載っているから，以下の問題が提起される．

「玉0を $n$ 個，玉1を $n + 1$ 個，玉2を $n + 2$ 個使って作るネックレス」と，「ピークを $n$ 個持つサイズ $2 n + 1$ のSchröder路」の一対一対応を作れ．

本記事ではこの全単射を構成してみた．

用語の準備

ネックレスの形式的な定義とかもここで述べておく．

ネックレスの形式的な定義

「円形に並べる」というのを巡回群の作用を使って以下のように定義する．
有限集合 $X$ 上の長さ $ℓ$ の語 $w = w_{0} \dots w_{ℓ - 1} (w_{i} \in X)$ と，位数 $ℓ$ の巡回群 $C_{ℓ} ≜ ⟨ a ∣ a^{ℓ} = e ⟩$ の元 $a^{i}$ に対して
$\begin{array}{r} a^{i} \cdot (w_{0} \dots w_{ℓ - 1}) ≜ w_{i} \dots w_{ℓ - 1} w_{0} \dots w_{i - 1} (i \in {0, \dots, ℓ - 1}) \end{array}$
と定義する．
語 $w$ に対して， $a^{0} \cdot w, \dots, a^{ℓ - 1} \cdot w$ によって得られる語たちを， $w$ の巡回シフトという．

語の集合
$W_{n} ≜ {w = w_{0} \dots w_{2 n} ∣ w は n 個の 0 と n + 1 個の 1 からなる}$
に対する，巡回群 $C_{2 n + 1}$ の作用が上記によって定義される．
「 $n$ 個の0と $n + 1$ 個の1を使って作るネックレス」とは，この作用による軌道である．（軌道とは作用によってうつり合う語を同値と定義したときの同値類である．）

また，語の集合
$V_{n} ≜ {w = w_{0} \dots w_{3 n + 2} ∣ w は n 個の 0 と n + 1 個の 1 と n + 2 個の 2 からなる}$
には，同様に巡回群 $C_{3 n + 3}$ の作用が定義される．
「 $n$ 個の0と $n + 1$ 個の1と $n + 2$ 個の2を使って作るネックレス」とは，この作用による軌道である．

格子路に関する用語の定義

Dyck路やSchröder路といった格子路に関する用語を定義する．

Dyck路

サイズ $n$ のDyck路とは，二つのベクトル $U ≜ (1, 1)$ と $D ≜ (1, - 1)$ からなる長さ $2 n$ の列
$v = (v_{1}, \dots, v_{2 n}) v_{i} \in {U, D}$
であって，二条件

任意の $i \in {1, \dots, 2 n}$ に対して， $v_{1} + \dots + v_{i} = (i, y_{i})$ とすると，
$y_{i} \geq 0$ ．
$v_{1} + \dots + v_{2 n} = (2 n, 0)$

を満たすものである．

Schröder路

サイズ $n$ のSchröder路とは，三つのベクトル $U ≜ (1, 1), D ≜ (1, - 1), L ≜ (2, 0)$ からなる列
$v = (v_{1}, \dots, v_{ℓ}) v_{i} \in {U, D, L}$
であって，二条件

任意の $i \in {1, \dots, ℓ}$ に対して， $v_{1} + \dots + v_{i} = (i, y_{i})$ とすると，
$y_{i} \geq 0$ ．
$v_{1} + \dots + v_{ℓ} = (2 n, 0)$

を満たすものである．

Schröder路の中で，ベクトル $U$ と $D$ がこの順番で連続する部分をピークという．

cycle lemmaと問題1の全単射

cycle lemmaを述べるために，dominating [6]という概念が必要になる．

dominating

語 $w = w_{0} \dots w_{2 n} \in W_{n}$ がdominatingであるとは，任意の $i \in {0, \dots, 2 n}$ に対して，語 $w_{0} \dots w_{i}$ に含まれる文字 $1$ の数が，それに含まれる文字 $0$ の数より多いことである．

dominatingを説明する例

dominatingな列の例： $11010, 1111000$
dominatingでない列の例： $011, 10101, 0010111$

以下の定理はcycle lemma [6]と呼ばれる.

cycle lemma

任意の語 $w = w_{0} \dots w_{2 n} \in W_{n}$ に対して，その巡回シフト
$w_{i} \dots w_{2 n} w_{0} \dots w_{i - 1}$ でdominatingなものが唯一つ存在する．

cycle lemmaを説明する例

語 $w = 0010111 \in W_{3}$ の巡回シフトは以下の $7$ つあり，そのうち $a^{4} \cdot w$ だけがdominatingである．
$\begin{aligned} a^{0} \cdot (0010111) & = 0010111, \\ a^{1} \cdot (0010111) & = 0101110, \\ a^{2} \cdot (0010111) & = 1011100, \\ a^{3} \cdot (0010111) & = 0111001, \\ a^{4} \cdot (0010111) & = 1110010, \\ a^{5} \cdot (0010111) & = 1100101, \\ a^{6} \cdot (0010111) & = 1001011, \end{aligned}$

cycle lemmaの証明．

列 $w \in W_{n}$ に含まれる文字0,1をそれぞれベクトル $U, D$ に置き換えることにより， $W_{n}$ の元を，点 $(0, 0)$ から出発して点 $(2 n + 1, y_{n})$ へ行く格子路とみなす．
格子路 $w \in W_{n}$ の節点のなかで「最も下にある点のうち，最も右にあるもの」が唯一つ存在する．その点を $(i, y_{i})$ とする．
すると $a^{i} \cdot w$ はdominatingであり， $a^{j} \cdot w (i \neq j)$ はdominatingではない．

問題1の解答．[6,7]

cycle lemmaより各同値類の代表元として，dominatingな語を一意的にとれる．よって，「玉0を $n$ 個，玉1を $n + 1$ 個使って作るネックレス」は $W_{n}$ のdominatingな語と一対一対応する． $W_{n}$ のdominatingな語の先頭にある $1$ を取り除き，文字0,1をそれぞれ文字 $D, U$ に変えるとDyck路を得る．この対応は一対一である．

全単射の例

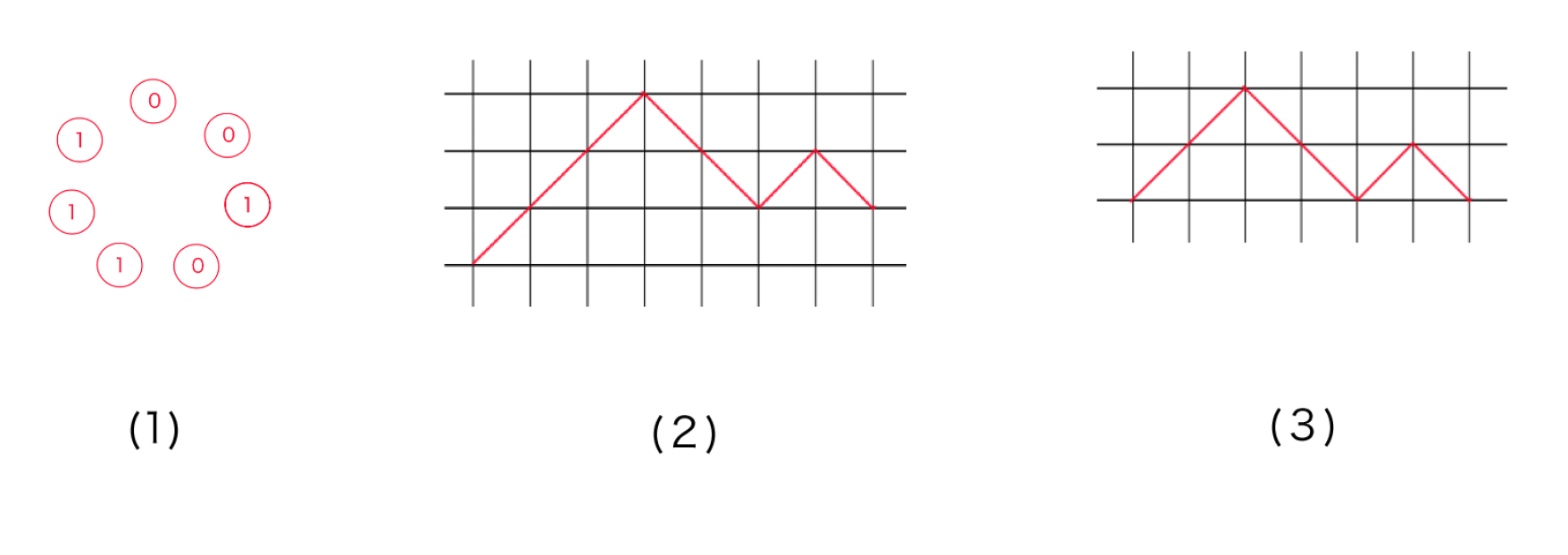
問題1の全単射の例
(1) ネックレス（＝軌道）．
(2) その軌道に含まれる唯一のdominatingな元 $1110010$ ．
(3) 先頭の1を取り去って作ったDyck路．

(1)と(2)は一対一対応していて，(2)と(3)も一対一対応する．

問題2の全単射

まず，玉が三種類の場合のdominatingを定義する．

玉が三種類の場合のdominating

語 $w = w_{0} \dots w_{3 n + 2} \in V_{n}$ がdominatingであるとは，任意の $i \in {0, \dots, 3 n + 2}$ に対して，語 $w_{0} \dots w_{i}$ に含まれる文字 $2$ の数が，それに含まれる文字1の数より多いことである．

玉が三種類の場合のdominatingを説明する例

dominatingな列の例： $202211$
dominatingでない列の例： $022211$

dominatingな列は必ず $2$ から始まる．下の例は先頭が $0$ なので，語 $0$ に含まれる文字 $2$ の数 (0個)が，それに含まれる文字 $1$ の数 (0個)より多くないため，dominatingではない．

玉が三種類のときもcycle lemmaと似た主張が成り立つ．

玉が三種類のときのcycle lemma

任意の語 $w = w_{0} \dots w_{3 n + 2} \in V_{n}$ に対して，その巡回シフト
$w_{i} \dots w_{3 n + 2} w_{0} \dots w_{i - 1}$ で (定義4の意味で)dominatingなものが唯一つ存在する．

玉が三種類のときのcycle lemmaの証明．

語 $w$ の巡回シフトたちを，文字 $0$ を無視すると同じになるものを同値とする同値関係により類別する．これらの同値類の代表元として，先頭が $0$ でないものを一意的に取ることができる．これら代表元たちのうちdominatingであるものが，定理3より唯一つ存在する．

問題2の解答．

「各節点に重さを付けたDyck路」というオブジェクトを定義する．
サイズ $n$ で重さ $m$ の「各節点に重さを付けたDyck路」とは，サイズ $n$ のDyck路 $v$ と，長さ $n + 1$ の非負整数列 $k = (k_{0}, \dots, k_{n})$ の組 $(v, k)$ で，
後者の和が $m$ ，つまり $k_{0} + \dots + k_{n} = m$ なるものである．
後者の非負整数列のことを重さの列ということにする．

定義4の意味でdominatingな列 $w \in V_{n}$ は，サイズ $n + 1$ で重さ $n$ の「各節点に重さを付けたDyck路」と一対一対応する．
なぜならば，文字0を無視すると，問題1よりdominatingな列 $w$ はサイズ $n + 1$ のDyck路と一対一対応し，その後合計 $n$ 個の0がどこに何個あったのかを重さの列として表せばよいからである．
例えば，dominatingな列 $220210121$ は， $0$ を無視すると $2221121$ だから，Dyck路 $UUDDUD$ と重さの列 $(0, 1, 0, 1, 0, 0, 0)$ の組に対応する．
絵で書くと以下のようなのを考えている．
各節点に重さを付けたDyck路!FORMULA[123][822804771][0]．サイズは!FORMULA[124][36213][0]で重さは!FORMULA[125][36182][0]である．各節点に重さを付けたDyck路 $(UUDDUD, 0101000)$ ．サイズは $3$ で重さは $2$ である．

次に，「サイズ $n + 1$ で重さ $n$ の各節点に重さを付けたDyck路」から「ピークを $n$ 個持つサイズ $2 n + 1$ のSchröder路」への一対一対応を作る．
サイズ $n + 1$ で重さ $n$ の各節点に重さを付けたDyck路
$(v, k) = ((v_{1}, \dots, v_{2 n + 2}), (k_{0}, \dots, k_{2 n + 2}))$
が与えられたとき，各 $i = 0, \dots, 2 n + 2$ について，列 $v$ の $v_{i}$ の直後に $(u d)^{k_{i}}$ を挿入する．但し， $(u d)^{k_{0}}$ は列 $v$ の先頭に挿入する．こうして作られた新しい列を $v^{'}$ とする．
例えば， $(UUDDUD, 0101000)$ が与えられたら，
$v^{'} = U u d UD u d DUD$
である．
次に， $v^{'}$ に含まれる連続する $UD$ をすべて $L$ に置き換える．こうしてできる列を $v^{″}$ とする．
例えば，上記の例では
$v^{″} = U u d L u d DL$
である．
最後に， $v^{″}$ に含まれる $u d$ を $UD$ に置き換え，これを $v^{‴}$ とする．
例えば，上記の例では
$v^{‴} = UUDLUDDL$
である．
こうして作られる列 $v^{‴}$ は，ピークを $n$ 個持つサイズ $2 n + 1$ のSchröder路である．この対応 $v \mapsto v^{‴}$ は一対一である．

全単射の例

以下は問題2の全単射の例を絵で描いたものである．
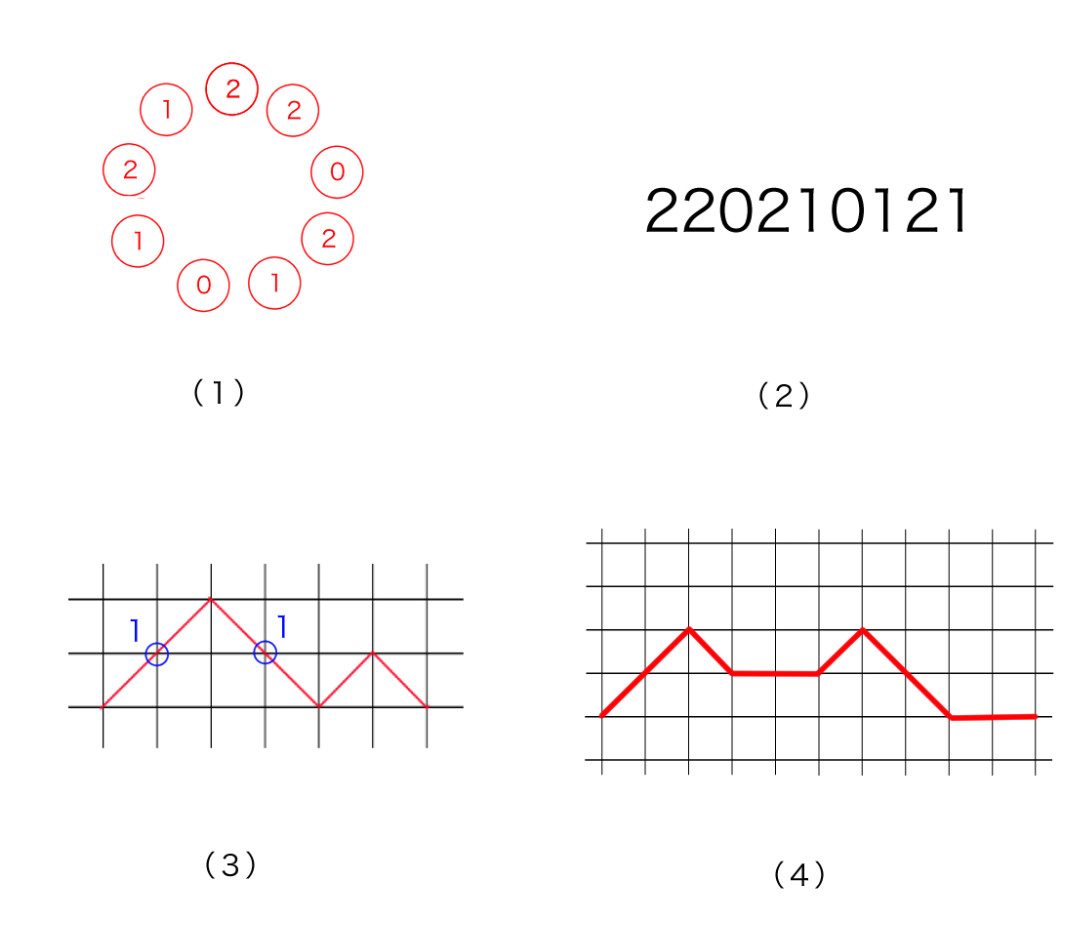(1) ネックレス (2) 軌道のdominatingな代表元 (3) 各節点に重さを付けたDyck路 (4) Schröder路
(1)と(2)，(2)と(3)，(3)と(4)はそれぞれ上で述べたように一対一対応しており，結果的に(1)と(4)は一対一対応する，