文献あり

巨大数学入門

①巨大数？グラハム数のことやろ←甘い！

グラハム数は、数学の証明に使われた最大の数として、ギネスブックに登録されている数だ。グラハム問題という、ある定理が成立するような、nのざっくりとした下限であるが、ここでは詳しく取り上げない。(ちなみに正確な下限に関しては未解決問題である)
まず、グラハム数の定義を確認しよう。
ここからの内容の変数は、全て自然数とする。
矢印表記は、私たちの、二項演算の拡張だ。
足し算をレベル1とする
a+a+a+…+a(b回)=a×b
掛け算は、足し算を繰り返したもの
これをレベル2とする
a×a×a×…×a(b回)=a^b
累乗は、掛け算を繰り返したもの
これをレベル3とする
a^a^a^…^a(b回)=a↑↑b
この続きに、テトレーション(tetration)を用意する。
テトレーションは、累乗を繰り返したもの
これをレベル4とする。
(tetra-tion)は、4番目(tetra)の演算子という意味で用いられているのだ)
既にある記号では表現できないから、新しい記号を作ろう。↑を用いることにする。
(累乗から交換則が成立しないため、右結合か左結合かで大きさが変化するが、対角化すると本質的な「大きさ」は一致する、グラハム数は、右結合を用いる)
10^100はGoogolと言って、宇宙空間の素粒子の総数と言われている。
10^10^100はGoogolplexと言って、さっきの話より、宇宙空間に10進数で表現できる最大の数くらいの大きさだ。
10↑↑10=10↑10↑10↑10↑10↑10↑10↑10↑10↑10 (Dekalogue)
この時点で、既に宇宙空間に数を記述するのはとっくに不可能なため、これ以降は現実世界に存在するものと比較する試みは全く意味をなさない。
ペンテーション(pentation)は、テトレーションを繰り返したもの
これをレベル5とする
a↑↑a↑↑a↑↑…↑↑a(b回)=a↑↑↑b
これを繰り返していこう。
二項演算子{n}を矢印n本として、
a{n-2}bはレベルnのa,b間の二項演算とする。
あと一歩!
f^を関数の合成として、
G(n)=3{n}3として、
G^64(4)がグラハム数だ!
え、大きさがイマイチ分からない？
視覚的に教えよう！
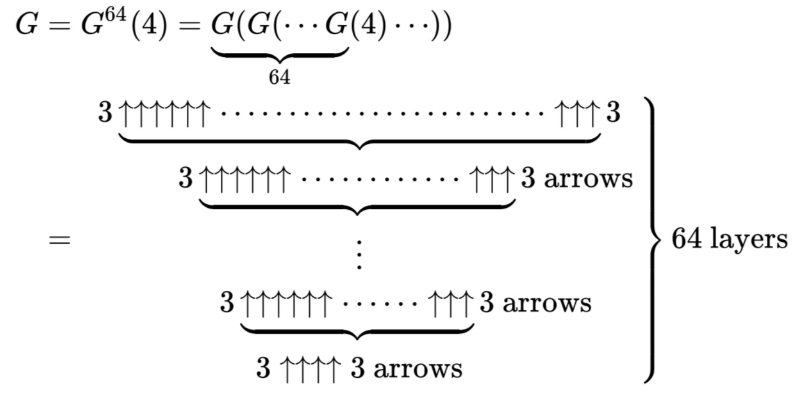視覚化した

あらゆる巨大数は、急増加関数を用いて近似される。急増加関数には可算順序数を組み込んで強化する。グラハム数に対応する順序数はω+1である。これは、巨大数のなかで小さい部類だ。
練習問題
(1)3↑x=E(x)
3↑↑↑3=E^k(3)　　(トリトリ)
このとき、kの値を求めよ。

★急増加関数の定義

君は初学者かもしれないが、唐突に急増加関数を学ばなければならない。
これから必要になるからだ。何も恐れなくていい。定義はたった3行だから。
簡単だ
ね、簡単でしょ？
君の疑問は既に想定している。順序数の定義がきっと分からないのだろう。
ざっくり教えよう。自然数1,2,3,4…の極限はωである。ωにはまた1を足して,
それを繰り返してω+1,ω+2,ω+3…の極限はω2である。さらに、
ω2+1,ω2+2,ω2+3…の極限はω3である。この操作を繰り返すと、
ω,ω2,ω3,ω4…の対角化だと気づかされる。極限はω^2だ。
さらにωの累乗の肩を増やすと、
ω,ω^2,ω^3…の極限はω^ω　ωが二段の指数タワーになる。
これも対角化していくと、
ω,ω^ω,ω^ω^ω…の極限をω↑↑ω=ε_0　イプシロン・ゼロ(イプシロン・ナル、イプシロン・ノート)って呼ぶことにする。
後続順序数とは、何かの順序数の次の順序数。つまり、ある順序数αを用いてα+1と表せる順序数だ。極限順序数は、そうでない順序数。(何らかの数列)…の極限αって定義できる。この、(何らかの数列)を基本列と呼び、αの基本列のn番目をα[n]って表すことにする。この具体的な定義が下の通りだ。
謎の[]の説明
この段階で、既に想像を絶する巨大数のレベルに到達できる。これを先に知ると、以降は現段階の限界より弱い、気楽なものになるだろう。
具体的に計算してみよう。
f0(x)=x+1
f1(x)=2x
f2(x)=x2x
f3(x)>2↑↑(x+1) (x>1)
fn+1(x)>2{n}x (x>1)
練習問題
(2) f2(x)≧2x+2　　(x>3)を証明して、
f3(x)>2↑↑(x+3) (x>12) を証明せよ。
(3) fω(x)<(x+1){x-1}(x+1) を証明せよ。
(4)アッカーマン関数を次のように定義する。
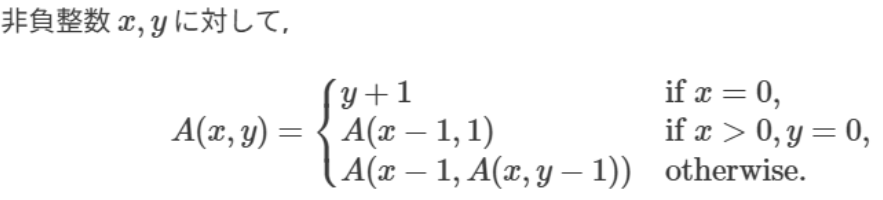アッカーマン関数
例えば、A(3,3)=61が成立する。
①A(x,y)=2{x-2}(y+3)-3　を証明せよ。(x≧3)
②fk(n+1)>A(k+1,n)を証明せよ。

②的確な対角化とは〜成功例と失敗例〜

これらは全て配列に関する表記だ。
いかに対角化を効率良く行うか、これが全てである。

下手くそな例ーコピー表記

※雑多な内容だから読み飛ばしても問題ありません。
定義を覗いてみよう。
ここで出現する×はハイパー数学の×である。
もちろんこれは累乗に置き換えても、大きさはほとんど変わらない。
このとき、ab=a↑↑b
a[b]=a↑↑↑bとなり、
a[b,c]=a{c}bである。
つまり、定義を少し変えると矢印表記の拡張になる。

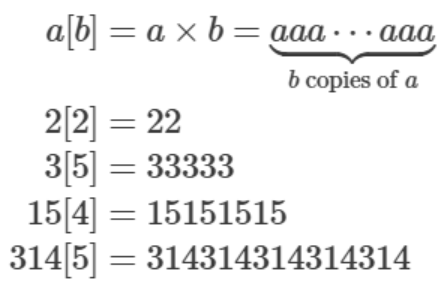定義
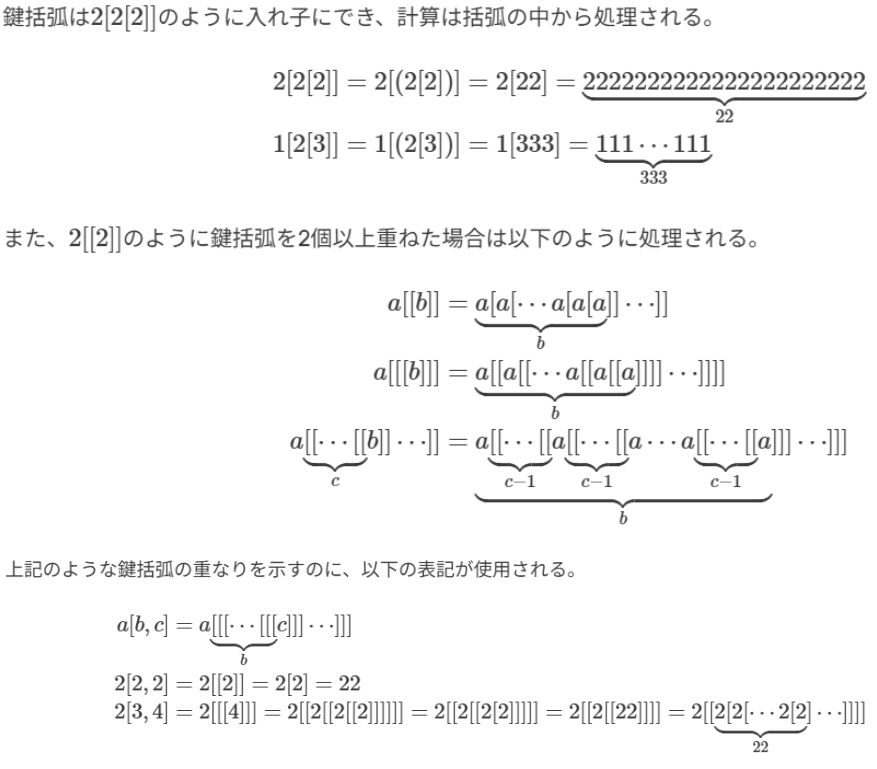画像の名前
画像の名前

この内容を急に全て理解しろと言われると戸惑うかもしれないが、
Googologistはすぐに解析できて当然である。
第一段階して、多重括弧を定義して、入れ子構造を用いてハイパー数学をベースに
レベルnの表記を定義してωレベルを実現している。
ここからが肝だ。
引数が3つのときを参照する。
a[b,c,d]≒a[a[b,c,d-1],a[b,c,d-1]]
いかつい入れ子構造を実現しているが、数を大きくするのに本質なのは、引数cである。
そのため引数bを入れ子にしてもほとんど大きくならない。
よって
a[b,c,d]≒a[b,a[b,c,d-1]]
ここでdを関数の合成回数と解釈して、
a[b,c]=f(c)として、a[b,c,d]≒f^d(c)が成立する。これはグラハム数と同等、ω+1レベルだ。
引数4つの時は、4つ目の引数は3つめの引数の関数として、反復合成するから、
ω+2レベル
引数5つのときは、5つ目の引数は4つめの引数の関数として、反復合成するから、
ω+3レベル
これを対角化することで、コピー表記の限界はω×2になる。
精密に考えてみよう。
n[n,n]<f_ω(n+2)は容易に証明できる。
これを利用して、
n[n,n,n]<f^(n+1)_ω(n+1)=f_ω+1(n+1)
n[n,n,n,n]<f_ω+2(n+1)
n[n,n…(m個)…n,n]<f_ω+m-2(n+1)
この表記はさらに拡張できる。
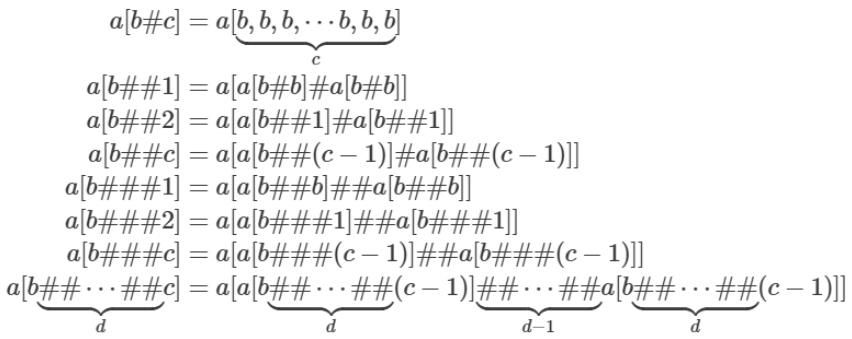画像の名前

しかしこれもたかがしれている。単純な計算でω3レベルだと分かる。本質的に対角化の手法が変っていないからだ。
練習問題
(5) n[n##…(n個)…##n]<f_ω3(n)を証明せよ。

中くらいの例ーチェーン表記

この表記は、矢印表記の自然な拡張として表記される。
まず、a{c}b=a→b→cと書き換える。
このとき、矢印表記のルールを
a{1}b=a^b
a{c}b=a{c-1}(a{c}(b-1))(b,c>1)、
a{c}1=a
というように定義を変えてもいい。
これはどういうことか。
cを1減らしてa{c-1}a…a{c-1}aという変換の長さがbであることは、cはそのまま、bが1少ないやつを右に代入するのと同じである。このとき、bは合成関数を実現するためのカウンターの役割を果たしている。
このルールを今後も適用しよう。配列の末尾が、強さに直接繋がるようにしたいから、カウンターはその一個手前にしよう。(実はこの安直な考えが、後々反省することになるが、今は一旦気にしない(騙される) ことにしよう)
a→b→c→1=a→b→cを前提に、
a→b→c→d=a→b→(a→b→(c-1)→d)→(d-1)
(b,c,d>1)は、
a→b→c=a→(a→(b-1)→c)→(c-1)
(b,c>1)の自然な拡張である。
ここから、さらに拡張をしていく。
矢印表記のルールは3個だが、
チェーン表記のルールは4個しかない。
𝑎→𝑏=𝑎^𝑏
𝑎→𝑏→𝑐→⋯→𝑦→𝑧→1=𝑎→𝑏→𝑐→⋯→𝑦→𝑧
𝑎→𝑏→𝑐→⋯→𝑦→𝑧→1→⋯=𝑎→𝑏→𝑐→⋯→𝑦→𝑧
𝑎→𝑏→𝑐→⋯→𝑦→𝑧=𝑎→𝑏→𝑐→⋯→(𝑎→𝑏→𝑐→⋯→(𝑦−1)→𝑧)→(𝑧−1)
(b,c,d,…,y,z>1)
この表記を評価していこう。
3→3→65→2はグラハム数より大きい。
練習問題
(6) 3→3→(n+1)→2=G^n(27)　を証明せよ。
次にこれ(コンウェイのテトラトリ)を展開していこう。
3→3→3→3=3→3→(3→3→27→2)→2
つまり、G^26(27)=Kとして、G^K(27)だ。
図で示すとこうなる
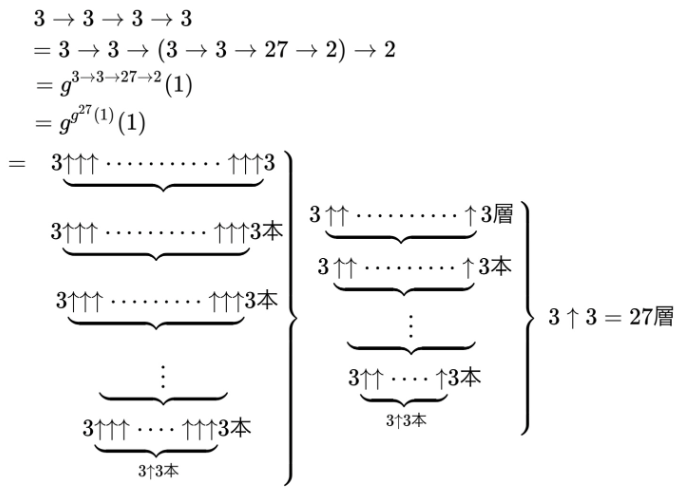画像の名前

一般にn→n→n→nはω+(n-1)レベルである。
3変数でωレベル
4変数でω2レベル……コピー表記の限界
5変数でω3レベル……拡張コピー表記の限界
6変数でω4レベル
…
n+2変数でωnレベル
グラハム数やコピー表記よりとても強力になるのは、末尾の変数を1増やす度に対応するレベルが1増えるからだ。つまり、チェーンの長さが1増える度にω増える。よって限界はω^2になる。
しかし、同じような配列表記で、もっと強化する手法がある。(次章)
拡張したものも紹介しよう。
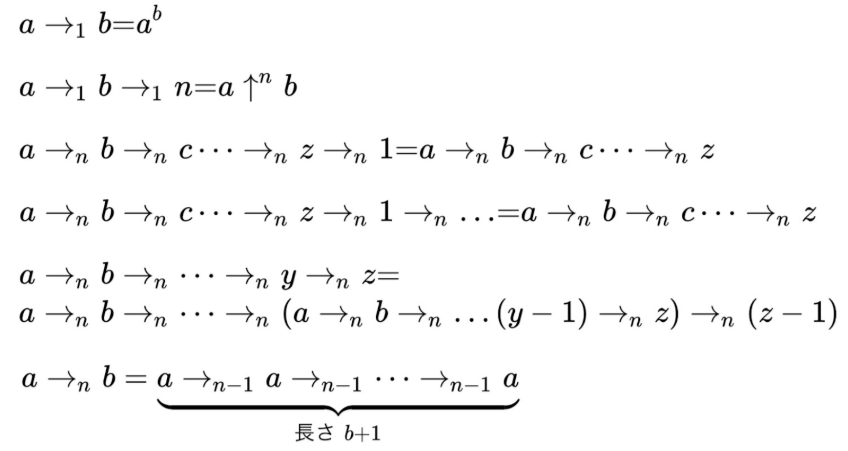拡張しました

注意事項:矢印のレベル(添え字)について、同じ配列中に異なる矢印が入っている場合は定義されない。

※n,b,c,d…,y,z>1
この表記の限界はω^3レベルだ。
ω^ωレベルには程遠い。
この定義を少し複雑に変更し、ω^ωレベルにする手法があるが、次の項目を見たら、煩雑な議論をしていたと気づくだろう。

上手な例ー線形配列表記

実は、たった4変数でω^2を表現する手法がある。
a{{1}}b=a{a{a{…{a}…}a}a}a(括弧がb-1個)とする。この配列を膨張(expanded)と呼ぶことにする。この時点でa{{1}}65はグラハム数よりも大きくなる。ここからさらに定義していこう。
a{{2}}b=a{{1}}a{{1}}a…(b回)…a{{1}}a (乗算膨張)
a{{3}}b=a{{2}}a{{2}}a…(b回)…a{{2}}a (冪乗膨張)
a{{4}}b=a{{3}}a{{3}}a…(b回)…a{{3}}a (膨張テトレーション)
…
真ん中の引き数を増やすたびにレベルに1を足しているため、この表記の限界はω2レベルである。もうコピー表記まで到達してしまった。しかし今後の定義も容易だ。
a{{{1}}}b=a{{a{{a{{…{{a}}…}}a}}a}}a(括弧がb-1個)
これを爆発(explosion)と呼ぶ。a{{{2}}}b,a{{{3}}}bも同様に定義できる。
a{{{{1}}}}b=a{{{a{{{a{{{…{{{a}}}…}}}a}}}a}}}a(括弧がb-1個)
これを爆轟と呼ぶ。爆轟とは何なのかを調べてみた。
関係ない話
恐らくtetration,pentationを捩ったものだろう。意味も併せて素晴らしいセンスだ。
波括弧の数が増えてきたので、記法を変化させるとともに、定義を少し変更する。
a{c}b={a,b,c}
a{{…{{c}}…}}b (括弧がd個)={a,b,c,d}
配列の入れ子構造の回数をbで表すのだから、チェーン表記の考え方と同様に、
2番目の引数を常に関数の合成回数を表すカウンターにするのが良さそうだ。
a{c}b=a{c-1}(a{c}(b-1))より、
{a,b,c}={a,{a,b-1,c},c-1}という変形の自然な拡張を意識して、
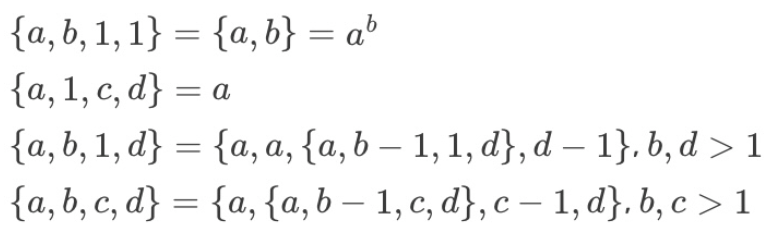自然な拡張
練習問題
(7)この定義の{a,b,c,4}が、これより前の定義の爆轟a{{{{c}}}}bに一致することを確認せよ。
なぜ大きくなるかは、これまでの全てをよんでいたら明白だ。コピー表記は、末尾の数が関数の合成を表すカウンターだから、長さがωに対応する。
チェーン表記は末尾から2番目が関数の合成を表すカウンター、末尾がωのカウンター、長さがω^2に対応する。
ここで、2つの表記に共通することは末尾以外のカウンターは常に死んでいる(変化しない)ことだ。
4変数線形配列表記は、2番目、3番目、4番目が常にアクティブなカウンターだから、たった4変数でω^2になる。2番目が関数の合成、3番目がレベルに1を足す役割、4番目がレベルにωを足す役割だからだ。ここから拡張するときに意識することは明らかだ。全ての引数を常にアクティブなカウンターにすることだ。
これを意識して拡張していこう。
5変数はこの通り
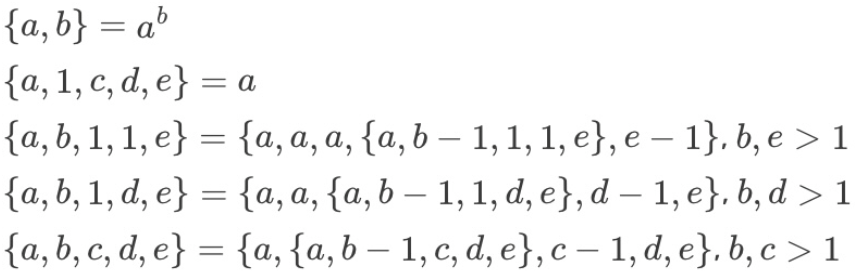5変数 5変数
6変数はこの通り
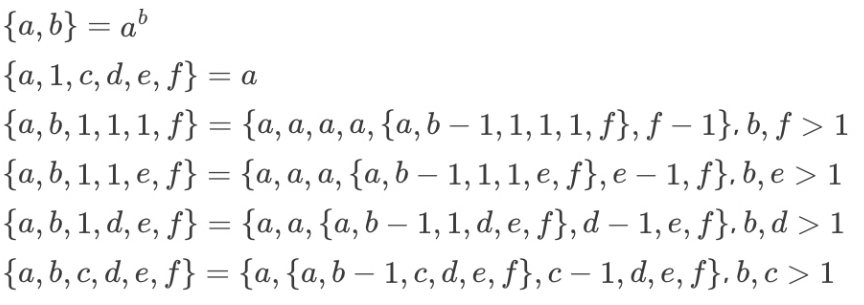6変数 6変数

今後の拡張も明白だろう。
ルールは矢印表記と変わらず、たった3ルールだ。
Bowersは次のように定義した。
bを基数(1つ目の引数)、pをプライム(2つ目の引数)とする。パイロットは、3つ目の引数以降で、初めて1でないもの、副操縦士はパイロットの1つ手前だ。(プライムとも一致しうる)副操縦士よりも前の配列の引数は全て乗客だ。
Aは現在の配列を表す。
①基数ルール
パイロットがいない場合（すなわち、プライムの後のすべての引数が1の時）
A= b^p
②プライムルール
プライムが1の時、 A= b
③破滅ルール
それ以外の時には、
1.副操縦士を元の配列のプライムを1減らしたものに置き換える。
3.パイロットの値を1減らす。
すべての乗客をbにする。
一方Birdは次のように定義した。
＃は長さ0以上の配列の一部を表し、変形前後で変化しない。
Rule 1. 引数が1つか2つなら、{a}= a, {a,b} = a^b(Rule 2の逆).
Rule 2. もし最後の引数が1なら、それは削除できる: {# 1} = {#}. (#記号は配列中の変わらない部分を表す。)
Rule 3. もし2番目の引数が1なら、その値は最初の引数となる: {a,1 #} = a
Rule 4. もし3番目の引数が1ならば:
{a,b,1,1,…,1,1,c #} = {a,a,a,a,…,a,{a,b-1,1,1,…,1,1,c #},c-1 #}
Rule 5. それ以外は:
{a,b,c #} = {a,{a,b-1,c #},c-1 #}
ここから定義される数も少し紹介しよう。
{3,3,3,3}…テトラトリ(コンウェイのテトラトリとは異なる
{4,4,4,4}…テトラテト
{10,10,10,10}…テトラデカル(tetradecal)
{10,10,10,10,10}…ペンタデカル(pentadecal)
{10,10,10,10,10,10,10,10,10,10}…イタラル(iteral)
{10,10,10,10,…(100個)…10,10}…グーボル(goobol)
この表記から、今回紹介する最大の数を作ろう
T(x)={10,10,10,…(x回)…10,10}として、
T^99(10)をギボル(Gibbol)とするよ。
線形配列表記と、急増加関数、アッカーマン関数の間に次の関係があるのが分かっている。
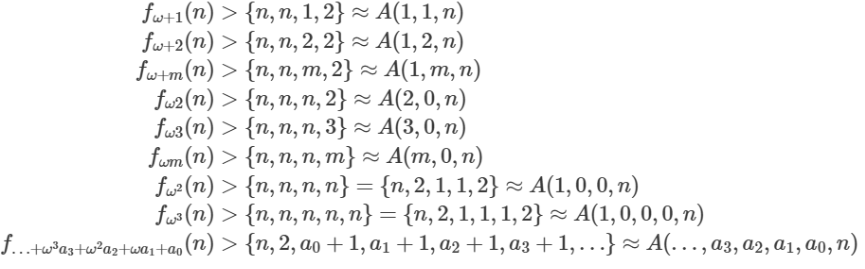これまでの表記との関係
練習問題
(8)
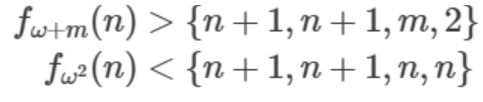これを証明しろ
(9)強配列表記を次のように定義する。
(チェーン表記と線形配列表記を比較するには、強配列表記を介在させると良い)
介在相手
次に、L(x)=3→3→3→…→3→3 (3がx回)とする。
①s(3,2,2,1,2)=L(x)のとき、xを求めよ。
②s(a,b,c,d)=a→a→a→…→a→b→c (矢印はd+1本)

★このことから、a→…→a→b→c (aがd個)<s(a,b,c,d)<{a,b,c,d}より、
具体的に、チェーン表記と4変数配列が同等だと分かる。
③n→mn<s(n,n,1,1,m)を証明せよ。(拡張チェーン表記を用いている)
実はこれらの議論によって重要なことが分かる。
①指数関数と1を引く操作、自身の配列のみ使える
②変形の条件分岐は単純である。(1か否か)
③配列の長さは常にそのままか、減少する。
このルールの元で作る配列表記の限界は、高々ω^ωである。
練習問題
(10)上記を証明せよ。
線形配列表記は、見事に限界の対角化をした。
この2人の表記は、元になっているものが一致しているが、定義の解釈が少し異なる。この少しの違いが、全然異なる方向へ拡張する、大きな違いを生む。
前者はBEAF(Bower’s Exploding Array Function)であり、後者がBAN(Bird’s Array Notation)である。前者は感覚的な理解に、後者は厳密な定義に特化している。

結論
巨大な数を作る本質は、ただ定義を複雑化することではない。基本となる表記を言い換えてより強く自然な拡張方法を模索したり、カウンター及び現在反映できる状態数を最大化すること。
迷ったら原点に戻ること。
これらが大切だ。
定義を読むだけでなく、どの部分が関数の強化の上で本質なのか見えるようになると、自ら新しい表記を作るのも容易い。

発展問題
(11)この表記は、矢印表記改だ。
新表記

この表記の限界はω^ωレベルだが、なぜなのかを説明しよう。これはω^ωレベルとは何なのか深い洞察である。
数を大きくするには、的確な対角化が必要だ。
もちろんε0以降の対角化の難易度は跳ね上がる。そもそもこれより大きい順序数を用意すること自体困難だからだ。次の項目に進もう。

③でかい数を作る最も早くてまあまあ困難な方法

ここからは理解を気にせず流し読みをしよう。
高校で習う計算は全て、足し算からスタートして、定義されている。これがペアノ算術だ。
皆の使うペアノ算術だけではε0を説明できない。ペアノ算術においては、f_ε0(n)という関数の強さを証明できない。例えば、グッドスタイン数列の収束性はペアノ算術で証明できないと証明されている。
これが、大学の集合論が必要になる理由。
可算順序数のみを用いる試みは、LVO程度で止まるのである(cf.ヴェブレン関数)。可算順序数をより大きくしたい場合、非可算順序数を用いる(cf.順序数崩壊関数)。Ω_ωに到達したら、次はΩ不動点、次にさらに大きな順序数が必要になるが…ここからはなんと現代数学の集合論ZFCでは限界があるのだ。ここからはさらに強力な独立命題が必要になるが、ZFCと矛盾している可能性もより高くなる。じゃあ、形式的な記号として巨大基数を用いることが可能かというと、それも慎重に扱わなければならない。
でかい順序数さえ作れたら巨大数を作れるというのが巨大数学の本質。とは言え、多くの名前のついた巨大数は、順序数を直接使わずに、対応関係だけ残して成り立っている。どういう対応を使うと大きくできるかは重要な考察だ。しかし、巨大数に王道はないと気づくだろう。

④うのの活動

巨大数学はグラフ理論と密接に繋がりがある
私が主に扱っている関数は
・Hydra(n)
・tree(n)
・TREE(n)
・SSCG(n)
・SCG(n)
・BH(n)
である。弱い順に書いた。どれも強力なグラフ理論の定理が背景になっている。
例えば、TREE及びtreeは、クラスカルの木定理が背景になっている。
どのくらい大きいの?
TREE(3)、tree(5)、SSCG(3)、SCG(1)、BH(4)はグラハム数や、より大きいどころか、今回学んだ順序数の限界ε0レベルも超えてしまう。当然入れる値が大きくなれば、想像を絶するほど大きくなる。詳しい値については、私の研究資料を覗くこと。