音階の構造を数学する
本記事は Mathlog Advent Calendar 2023 大学数学部門 の19日目の記事です．
本記事では，ピタゴラス音律や平均律といった音律の理論は一切扱いません．特に周波数比に基づく音律・音階の生成を数学的に解説した記事ではありません．
こうした話題に関心がある方は，例えば
- 数学好きのための音楽理論入門！！ （ みゆ🌹 ฅ^•ω•^ฅ ＠ 数学を愛する会 さんによるMathlog記事）
- Clader, Emily. Why Twelve Tones?
- 坂崎 紀『音律入門』
- Loy, Gareth. (2006). Musimathics, Volume 1: The Mathematical Foundations of Music. The MIT Press.
- Sethares, Willian A. (2005). Tuning, Timbre, Spectrum, Scale (2nd ed.). Springer.
- Spitzer, Shay Joel Francis. (2023). Mathematical Structure of Musical Tuning Systems. Senior Projects Spring 2023, 229.
などをご覧ください．
イントロダクション
』より引用](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FGmhbTa8kHvVSlwkl8nQS.png?alt=media)
伝統的な音楽理論では，音階は音律とともに，音響学的な説明によって基礎付けられることがほとんどです．特に，「音楽と数学」をテーマとする何らかの文書を読んだことのある方は，恐らく，周波数比に基づくピタゴラス音律の生成や，その派生形（純正律，平均律，中全音律など）についての数学的な議論を目にしたのではないかと思います．
しかし通常，作曲をする上では，こうした音響学的な議論はほぼ問題になりません．既に現代では，特別な理由がない限り平均律を用いることが標準となっていますし，仮に別の音律を用いたとしても，よほどのことでない限り「異なる音律で演奏された同じ音楽」として認識されるのであって，それで音楽そのものが何か本質的に変わるわけではないからです（そもそも音律の違いすら聴き取れない人も多いと思います）．音や和音そのものの質という個別的な問題を扱うのが音律だとすれば，むしろ作曲家がより扱っているのは，音や和音の間の唯名的な関係性，すなわち構造ではないでしょうか．
例えば，$A_4, C \sharp_5, E_5$という対象について考えてみましょう．純正律では，これらはそれぞれ
$$
\begin{align}
A_4 & \mapsto 440 \text{ Hz} \\
C \sharp_5 & \mapsto 550 \text{ Hz} \\
E_5 & \mapsto 660 \text{ Hz}
\end{align}
$$
と規定されますが，平均律では
$$
\begin{align}
A_4 & \mapsto 440 \text{ Hz} \\
C \sharp_5 & \mapsto 440 \times 2^{3/12} \approx 554.4 \text{ Hz} \\
E_5 & \mapsto 440 \times 2^{7/12} \approx 659.3 \text{ Hz}
\end{align}
$$
と規定されます．
一方，私たちが馴染んでいる音楽理論（和声理論，コード理論など）ではこうした個々の音の調律といった個別的規定は捨象され，「$A$メジャーコードの構成音である」とか「$D$メジャースケールに含まれている」とか「$A_4, C \sharp_5$間の音程は長3度である」といった「関係性」がそのまま問題とされていることが分かるでしょう．
すると，音階が持つこうした構造を数学的に書き表すことで，数学的手法を用いて音階に関する諸事実を発見する，という音階研究のあり方が考えられます．
さて，学術分野としての音楽理論では，'80年代後半から，こうした音階の構造に関する数学的研究が発達しており，ダイアトニック・セット理論（diatonic set theory）と呼ばれる領域も誕生しています．同じ「音楽と数学」であるとはいえ，その性格は音律の理論とは対照的です．本記事では，その基本的な部分を簡単に紹介します．
準備
ピッチクラス
左右方向に無限に広い理想的なピアノの鍵盤を考えてみましょう．このピアノの各鍵盤に対応する，$C_2$や$F \sharp_6$のような名前をピッチ（音高，pitch）と呼びます．
私たちが普段$C$という音名で呼んでいるものは，実際には$\dots, C_2, C_3, C_4, C_5, C_6, \dots$といった整数オクターブだけ異なるピッチたちを一つにまとめたものです．つまり，
$$ C = \{C_i : i \in \bbZ\}$$
です．同様の操作を他のピッチに対しても行えば，
$$
\begin{align}
& C, C \sharp, D, D \sharp, E, F, \\
& F \sharp, G, G \sharp, A, A \sharp, B
\end{align}
$$
という12種類の「ピッチのクラス」を得ることができます．簡単のため，これらをこの順に$0$から$11$の整数で表し，ピッチクラス（pitch class, PC）と呼びます．音名とピッチクラスの対応は以下の通りです．
| 音名 | ピッチクラス | 音名 | ピッチクラス |
|---|---|---|---|
| $C$ | $0$ | $F \sharp$ or $G \flat$ | $6$ |
| $C \sharp$ or $D \flat$ | $1$ | $G$ | $7$ |
| $D$ | $2$ | $G \sharp$ or $A \flat$ | $8$ |
| $D \sharp$ or $E \flat$ | $3$ | $A$ | $9$ |
| $E$ | $4$ | $A \sharp$ or $B \flat$ | $10$ |
| $F$ | $5$ | $B$ | $11$ |
全てのピッチクラスの集合$\{0, \dots, 11\}$をPC空間（PC space）と呼びます．オクターブ差さえ無視すれば，私たちの音楽はこの中で展開されると思うことができます．$B_4$の次のピッチが$C_5$であることからも分かるように，$11$-$0$間は隣接しているので，PC空間は以下のような循環構造を持っていることが分かります．
![PC空間!FORMULA[49][-2099443194][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FfwTqeZcquHzCMDem2a4w.png?alt=media)
PC空間$\bbZ_{12}$
この記事の本筋ではないですが，ここまでの流れを数学的に理解するなら
- ピッチの集合（$\bbZ$で表せる）を，整数オクターブだけ異なるピッチの集合（$12 \bbZ$で表せる）で割る．
- 剰余類環$\bbZ_{12} \simeq \{0, \dots, 11\}$をPC空間として得る．
というように理解できます．
PCセット
ピッチクラスの空でない集合をPCセット（PC set）と呼びます．同じことですが，これはPC空間$\bbZ_{12}$の空でない部分集合です．
- $C$メジャーコード（構成音$C, E, G$）：$\{0, 4, 7\}$
- $C$ダイアトニックスケール（構成音$C, D, E, F, G, A, B$）：$\{0, 2, 4, 5, 7, 9, 11\}$
上の例から示唆されるように，PCセットは文脈によって，スケール（音階，scale）やコード（chord）とも呼ばれます．スケール$X$は，$\# X = d$であるとき$d$音スケールであるといいます．例えば$C$ダイアトニックスケールは7音スケールです．
上記の定義から分かるように，スケールは中心音の情報を持ちません．スケールに中心音の情報を付加したものはモード（旋法，mode）と呼ばれます．例えば$C$ダイアトニックスケールは7音スケールなので，各音を中心音とする7つの旋法を一挙に扱っているものとみなせます（cf. Mode (music) - Wikipedia ）．
PC空間上に$C$ダイアトニックスケール$\{0, 2, 4, 5, 7, 9, 11\}$を図示すると，以下のようになります．
![!FORMULA[67][-2099443194][0]上での!FORMULA[68][36709][0]ダイアトニックスケールの表現](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FlljBgJUMJP1PrkWVpAxK.png?alt=media)
$\bbZ_{12}$上での$C$ダイアトニックスケールの表現
音階の一般化
さて，音楽にはダイアトニックスケール以外にも多くのスケールが存在します．身近な所では ホールトーンスケール や オクタトニックスケール がそうであり，また微分音音楽ではそもそも$\bbZ_{12}$以外のPC空間内でスケールが構成されます．
そこで思い切って，任意のピッチ空間における任意のスケールを考えることにしましょう．とはいえ，12と7をそれぞれ任意の正の整数$c$と$d$に変更すればよいだけです．
- ある正の整数$c$をクロマティック基数（chromatic cardinality）という．
- クロマティック基数$c$に対し，$\bbZ_c$をPC空間（PC space）という．
- PC空間の要素をピッチクラス（pitch class, PC），空でない部分集合をPCセット（PC set）という．PCセットはスケール（scale）とも呼ばれる．
- スケール$X \sbse \bbZ_c$に対し，$\# X = d$であるとき，$X$は$d$音スケール（$d$-note scale）であるという．
generic／specificの区別
音程は離散的な距離と思うことができますが，スケール上で同一の音程であったとしても，PC空間から見れば異なる音程であるということがあります．例えば，$C$ダイアトニックスケールにおいて，0-4（$C$-$E$）間の音程と2-5（$D$-$F$）間の音程は，スケール上で見ればどちらも2（度数法でいう3度）ですが，PC空間上で見ればそれぞれ4と3になります（度数法でいう長3度と短3度）．
このように，ある音程をスケール内部から見たときの値をgeneric音程（generic interval），スケール外部から見たときの値をspecific音程（specific interval）といいます．これは度数法の一般化と捉えることができます．
音階理論では，音程に限らず，あるものをスケール内部／外部から見ているということを表すためにgeneric／specificという形容詞を用いることがしばしばあります．
maximal evenness (ME)
先ほども見たように，$C$ダイアトニックスケールの構成音でgeneric音程2を作ると，以下のようにspecific音程4と3の全2種類の音程を得られることが分かります．
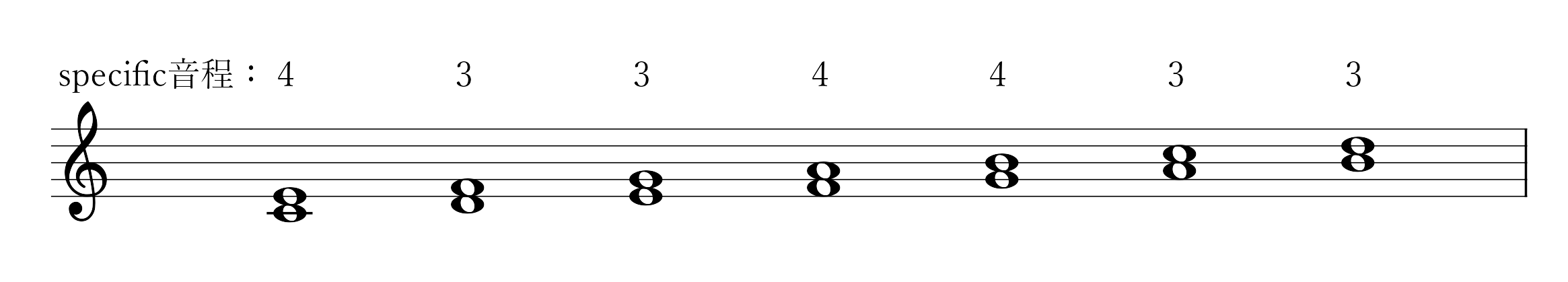generic音程2がなすspecific音程
さらにgeneric音程1の場合を試してみると，やはりspecific音程2と1の全2種類の音程を得られることが分かります．
generic音程1がなすspecific音程
実は，以下が成り立ちます．
$C$ダイアトニックスケールにおいて，generic音程$I \in \bbZ_7 \setminus \{0\}$は常に2種類のspecific音程を形成する．さらに，それらは連続する2整数である．
この性質はconsecutivity propertyと呼ばれるのですが，これを少し緩めたmaximal evennessと呼ばれる性質は，様々な興味深い性質をスケールに与えることが知られています．
以降，簡単のため$x \bmod n$を単に$(x)_n$と書きます．また断りのない限り，スケール$X$に対し，$X_i$を$i$番目に小さい$X$の要素とします（$i \ge 0$）．
$X \sbse \bbZ_c$を$d$音スケール，$I \in \bbZ_d$をgeneric音程とする．$X$における$I$のスペクトル（spectrum）$\spec_X (I)$を以下で定める．
$$ \spec_X (I) = \{(X_{(k + I)_c} - X_k)_c : k \in \bbZ_d\}$$
$d$音スケール$X \sbse \bbZ_c$がmaximally even（ME）であるとは，任意のgeneric音程$I \in \bbZ_d \setminus \{0\}$に対し，$\spec_X (I)$が1つの整数または連続2整数のみを要素に持つことをいう．
実は，私たちの親しんでいる様々なスケールがMEを満たすことが知られています．
- augコード：$\{0, 4, 8\}, \{1, 5, 9\}, \{2, 6, 10\}, \{3, 7, 11\}$
- dim7コード：$\{0, 3, 6, 9\}, \{1, 4, 7, 10\}, \{2, 5, 8, 11\}$
- ダイアトニックスケール：$\{0, 2, 4, 5, 7, 9, 11\}$など全12種
- ペンタトニックスケール：$\{0, 2, 4, 7, 9\}$など全12種
- ホールトーンスケール：$\{0, 2, 4, 6, 8, 10\}, \{1, 3, 5, 7, 9, 11\}$
- オクタトニックスケール：$\{0, 1, 3, 4, 6, 7, 9, 10\}, \{1, 2, 4, 5, 7, 8, 10, 11\}, \{0, 2, 3, 5, 6, 8, 9, 11\}$
さて，MEと類似する性質の一つに，Myhill性という性質があります．
$d$音スケール$X \sbse \bbZ_c$がMyhill性（Myhill's property）を持つとは，任意のgeneric音程$I \in \bbZ_d \setminus \{0\}$に対し，$\spec_X (I)$が2つの異なる整数のみを要素に持つことをいう．
MEとMyhill性の間には，比較的簡単にわかる以下の関係があります．
$\gcd (c, d) = 1$のとき，MEなスケールはMyhill性を持つ．
$X \sbse \bbZ_c$をMEなスケールとする．$X$がMyhill性を持たないと仮定し，$\gcd (c, d) \neq 1$を示す．MEとMyhill性の定義より，$\spec_X (I)$は常に1つの整数のみを要素に持つ．$\spec_X (1) = \{h\}$なる$h$を取る．
$$ c = \sum_{k = 0}^{d - 1} (X_{(k + 1)_d} - X_{k})_c = \sum_{k = 0}^{d - 1} h = dh$$
を得，よって$\gcd (c, d) \neq 1$を得る．
さて，Myhill性より少し強い，reducedと呼ばれる状況を考えてみましょう．
- $d$音スケール$X \sbse \bbZ_c$が還元されている（reduced）とは，$\spec_X (1)$が連続2整数のみを要素に持つことをいう．
- $d$音スケール$Y \sbse \bbZ_{c'}$が$d$音スケール$X \sbse \bbZ_{c}$から還元されている（reduced from）とは，$f (Y) = X$となるような順序同型写像$f \colon \bbZ_{c'} \to \bbZ_c$が存在し，かつ$Y$が還元されていることをいう．
2.の$X$を$Y$に還元する操作は要するに，スケール$X \sbse \bbZ_c$があるとして，$X$が還元されたスケールになるように$\bbZ_c$から非スケール音を適当に取り除くイメージです．
還元とMyhill性の間には以下の関係が成り立ちます．この定理は後々「cardinality equals variety」の章で重要な定理を導くのに用いられます．
$d$音スケール$Y \sbse \bbZ_{c'}$は$d$音スケール$X \sbse \bbZ_{c}$から還元されているとする．$Y$がMyhill性を持つならば，$\gcd (c', d) = 1$である．
まず以下の補題を示します．
$X \sbse \bbZ_c$を$d$音スケールとする．任意のgeneric音程$I \in \bbZ_d$に対し，以下が成り立つ．
$$ \sum^{d - 1}_{k = 0} (X_{(k + I)_d} - X_k)_c = c I$$
$$ \begin{align} \sum^{d - 1}_{k = 0} (X_{(k + I)_d} - X_k)_c & = \sum^{d - 1}_{k = 0} \sum^{I - 1}_{l = 0} (X_{(k + I + 1)_d} - X_{(k + l)_d})_c \\ & = \sum^{I - 1}_{l = 0} \sum^{d - 1}_{m = 0} (X_{(m + 1)_d} - X_{m})_c \\ & = \sum^{I - 1}_{l = 0} c \\ & = c I \end{align} $$
（更新：2023.12.30）このセクションのこれ以降の部分は修正中です．
well-formedness (WF)
ダイアトニックスケールに関する有名な事実の一つに，「適切な音を始点とし，完全5度堆積を6回繰り返せばダイアトニックスケールを『生成』できる」というものがあります．
完全5度堆積．連続する7音を選ぶとダイアトニックスケールになる．
ところで，この方法による$C$ダイアトニックスケール$X = \{0, 2, 4, 5, 7, 9, 11\}$の生成列を，$i$番目に小さい$X$の要素$X_i$によって表示してみると以下のようになります．
![!FORMULA[157][-1290932240][0]の生成順は，添え字を!FORMULA[158][-290712746][0]することで再現できる．](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FysfSZeweo5Pe221WaseA.png?alt=media)
$X = \{0, 2, 4, 5, 7, 9, 11\}$の生成順は，添え字を$+ 4 \bmod 7$することで再現できる．
これを見ると，添え字列も$+ 4 \bmod 7$によって生成されていることが分かります．
このように，スケールが「生成」される順番を，添え字列の「生成」によって再現できるという性質をwell-formednessと呼びます．
$X \sbse \bbZ_c$を$d$音スケール，$g \in \bbZ_c$をspecific音程とする．以下を満たす$s \in X$が存在するとき，$X$は$g$によって生成される（generated）という．
$$ X = \{(s + g I)_c : I \in \bbZ_d \}$$
また，そのような$g$を$X$の生成音程（generating interval）という．
$X \sbse \bbZ_c$を$g$によって生成される$d$音スケールとする．
- $X$がwell-formed（WF）であるとは，以下が任意の$I \in \bbZ_d$に対して成り立つような$h, i \in \bbZ_d$が存在することをいう．
$$ X_{(i + h I)_d} = (X_i + g I)_c$$ - $X$が非退化well-formed（non-degenerate well-formed）であるとは，$X$がWFであり，かつ$\gcd (c, d) = 1$であることをいう．
$C$ダイアトニックスケール$X = \{0, 2, 4, 5, 7, 9, 11\}$は（1）$g = 7$によって生成され，（2）非退化WFである．実際，
- 以下のように生成される．
$$ \{(5 + 7 I)_{12} : I \in \bbZ_7\} = \{5, 0, 7, 2, 9, 4, 11\} = X$$ - また$\gcd (12, 7) = 1$であり，各$I \in \bbZ_7$に対し，
$$ X_{(3 + 4 I)_7} = (5 + 7 I)_{12} = (X_3 + 7 I)_{12}$$
が計算によって確かめられる．
ME，Myhill性，WFの関係
証明を書くと長くなるので割愛しますが，以下が成り立つことが知られています．
$\gcd (c, d) = 1$のとき，MEなスケールは非退化WFである．
実は，(Carey and Clampitt 1996)では，全く別個に定義されたかのように見えたMyhill性と非退化WFが実は等価であることが証明されています．
以下は同値である．
- スケールがMyhill性を持つ．
- スケールが非退化WFである．
cardinality equals variety (CV)
さて，作曲を行うにあたっては，あるスケール上でどれだけの「種類」のメロディーやコードを作れるかが重要な問題となってきます．ここでは，同じgeneric構造を持つメロディーやコードが何種類あるかを考えてみましょう．
列に関するCV（LCV）
$X$を$d$音スケール，$k$を正の整数，$0 \le n_0, \dots, n_{k - 1} \le d - 1$とする．
- $\langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$を$X$上のPC列（sequence of PC）という．
- $X_{n_0}, \dots, X_{n_{k - 1}}$のうち相異なるものの数を，PC列$\langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$の基数（cardinality）といい，$\# \langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$と書く．
PC列とは要はメロディーのことです．
PC列を「スケール上で」平行移動させるという操作を定義します．
$X \sbse \bbZ_c$を$d$音スケール，$S = \langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$を$X$上のPC列，$I \in \bbZ_d$をgeneric音程とする．$S$の$I$-generic移置（$I$-generic transposition）$t_I (S)$を以下で定める．
$$ t_I (S) = \langle X_{(n_0 + I)_d}, \dots, X_{(n_{k - 1} + I)_d} \rangle$$
$X \sbse \bbZ_c$を$d$音スケール，$S = \langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$を$X$上のPC列とする．
- $S$のgenus$\gen (S)$を以下で定める．
$$ \gen (S) = \{t_I (S) : I \in \bbZ_d\}$$ - $S$のspecies$\sp (S)$を以下で定める．
$$ \sp (S) = \langle (X_{n_1} - X_{n_0})_c, \dots, (X_{n_{k - 1}} - X_{n_{k - 2}})_c \rangle $$
$X$が$C$ペンタトニックスケール$\{0, 2, 4, 7, 9\} \sbse \bbZ_{12}$，$S$がPC列$\langle 7, 2, 9, 2 \rangle$の場合，$I \in \bbZ_{5}$に対する$t_I (S)$を列挙すると，
$$
\begin{align}
t_0 (\langle 7, 2, 9, 2 \rangle) & = \langle 7, 2, 9, 2 \rangle \\
t_1 (\langle 7, 2, 9, 2 \rangle) & = \langle 9, 4, 0, 4 \rangle \\
t_2 (\langle 7, 2, 9, 2 \rangle) & = \langle 0, 7, 2, 7 \rangle \\
t_3 (\langle 7, 2, 9, 2 \rangle) & = \langle 2, 9, 4, 9 \rangle \\
t_4 (\langle 7, 2, 9, 2 \rangle) & = \langle 4, 0, 7, 0 \rangle
\end{align}
$$
となる．それぞれのspeciesは
$$
\begin{align}
\sp (\langle 7, 2, 9, 2 \rangle) & = \langle 7, 7, 5 \rangle \\
\sp (\langle 9, 4, 0, 4 \rangle) & = \langle 7, 8, 4 \rangle \\
\sp (\langle 0, 7, 2, 7 \rangle) & = \langle 7, 7, 5 \rangle \\
\sp (\langle 2, 9, 4, 9 \rangle) & = \langle 7, 7, 5 \rangle \\
\sp (\langle 4, 0, 7, 0 \rangle) & = \langle 8, 7, 5 \rangle \\
\end{align}
$$
となる．
$X \sbse \bbZ_c$を$d$音スケールとする．$X$が列に関してCV（line CV, LCV）であるとは，任意のPC列$S = \langle X_{n_0}, \dots, X_{n_{k - 1}} \rangle$に対し，
$$ \# S = \# \{\sp (T) : T \in \gen (S)\}$$
であることをいう．
上記の例では
$$ \# \langle 7, 2, 9, 2 \rangle = 3 = \# \{\sp (T) : T \in \gen (\langle 7, 2, 9, 2 \rangle)\}$$
となり，LCVが部分的に満たされています．これが任意のPC列に対して成り立つというのがLCVの主張です．
こちらも証明がやや長くなるので省略しますが，実は以下が成り立つことが知られています．
Myhill性を持つスケールはLCVである．
ダイアトニックスケールやペンタトニックスケールはMyhill性を持つので，これらはLCVを満たします．つまり$n$音の異なるピッチクラスからなるメロディーをスケール上で平行移動させても，ちょうど$n$種類のgeneric構造を持つメロディーしか生成できないことが言えるわけです．
ここから更に以下が証明できます．
以下は同値である．
- スケールがLCVである．
- スケールが非退化WFである．
「非退化WF$\Leftrightarrow$Myhill性」であるから，「LCV$\Leftrightarrow$Myhill性」を示せばよい．
$\Leftarrow$は前定理による．
$\Rightarrow$を示す．$X$をスケールとする．PC列$S = \langle X_{n_0}, X_{n_1} \rangle$に対し，
$$ \gen (S) = \{\langle X_{n_0}, X_{n_1} \rangle, \dots, \langle X_{(n_0 + d - 1)_d}, X_{(n_1 + d - 1)_d} \rangle\}$$
を得，よって
$$ \{\sp (T) : T \in \gen (S)\} = \{\langle \langle X_{n_1} - X_{n_0} \rangle \rangle, \dots, \langle \langle X_{(n_1 + d - 1)_d} - X_{(n_0 + d - 1)_d} \rangle \rangle\}$$
を得るが，LCVより，これは$\# S = 2$元集合である．よって，Myhill性が成り立つ．
コードに関するCV（CCV）
さてこの結果を見ると，PC列だけではなくコード（PCセット）に対しても同様のことが言えるのではないかという予想が生じます．スケールのこの性質をコードに関してCV（chord CV, CCV）であるといいます．
もちろん，コードのgenusやspeciesを定義せねばならないのですが，自然に行えるので省略します．ここでは，generic音程に関して平行移動できるコードは同じgenusに属し，specific音程に関して平行移動できるコードは同じspeciesに属するものと思えばよいです．
![!FORMULA[242][36709][0]ダイアトニックスケールの場合の例．(a)-(c)は全て同じgenusに属するが，(a)(b)と(c)は異なるspiecesに属する．](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FrXRL96uH6ZH2mEpvR7Zm.png?alt=media)
$C$ダイアトニックスケールの場合の例．(a)-(c)は全て同じgenusに属するが，(a)(b)と(c)は異なるspiecesに属する．
先ほどの定理6を見ると，以下が成り立つように思われます．
$X$をMyhill性を持つスケールとする．PCセット$Y \sbse X$に対し，$Y$と同genusのPCセットは，$\# Y$種類の異なるspeciesを形成する．
が，これは成立しません．まず明らかな反例として，$Y$が$X$と一致する場合が挙げられます．このとき$Y$と同genusのPCセットは明らかに$Y$自身しか存在しないため，形成されるspeciesも1種類のみになります．
では，「$Y \sbse X$」を「$Y \subset X$」に改めれば成り立つかというと，こちらも一般には成り立ちません．
$X = \{0, 1, 2, 4, 5\} \sbse \bbZ_{7}$，$Y = \{0, 1, 4\}$の場合を考える．$X$はMyhill性を持つ．しかし$Y$と同genusのPCセットは
$$ \{0, 1, 4\}, \{1, 2, 5\}, \{0, 2, 4\}, \{1, 4, 5\}, \{0, 2, 5\}$$
であり，これらは2種類のspeciesしか形成せず，$\# Y = 3$と一致しない．
スケールがCCVであるための必要十分条件については，(Clampitt 2008)によって次が得られています．
$X \sbse \bbZ_c$を$d$音スケールとする．以下は同値である．
- $X$はCCVである．
- $X$は非退化WFで，かつ$d$は以下を満たす素数である．
$$ d \le \left\lfloor \frac{c}{2} \right\rfloor + 1$$
$J$関数
ここまでは，与えられた$c, d$に対応するMEなスケールを発見しようと思うと，試行錯誤でそれらしきスケールを選び，いちいちMEの定義を満たしているかを確かめるしかありませんでした．しかし，実は$\gcd (c, d) = 1$の場合，MEなスケールを生成する公式が存在します．
$\gcd (c, d) = 1$を満たす正の整数$0 < d < c$と$m \in \bbZ_c$に対し，$J$関数（$J$-function）$J^m_{c, d} : \bbZ_d \to \bbZ_c$を以下で定める．
$$ J^m_{c, d} : x \mapsto \left( \left\lfloor \frac{c x + m}{d} \right\rfloor \right)_c$$
$m$をモード指数（mode index）という．
$c = 12$，$d = 7$の場合，像$J^m_{12, 7} (\bbZ_7)$を計算すると以下のようになる．
- $m = 0$の場合：$\{0, 1, 3, 5, 6, 8, 10\}$（$D \flat$ダイアトニックスケール）
- $m = 1$の場合：$\{0, 1, 3, 5, 7, 8, 10\}$（$A \flat$ダイアトニックスケール）
- $m = 2$の場合：$\{0, 2, 3, 5, 7, 8, 10\}$（$E \flat$ダイアトニックスケール）
- （中略）
- $m = 11$の場合：$\{1, 3, 5, 6, 8, 10, 11\}$（$F \sharp$ダイアトニックスケール）
2次MEセット
MEのセクションで，$\bbZ_{12}$におけるMEなPCセットの例としてaugコードやdim7コードを挙げましたが（「スケール」も「コード」も「PCセット」の別名であることを思い出しましょう），それらよりも遥かに利用頻度の高いメジャーコードやマイナーコード，あるいはM7コードやm7コードは登場しません．実際，これらが$\bbZ_{12}$でMEでないことは明らかです．ではこれらはMEという視点では捉えられない対象なのでしょうか．
実は，そのようなPCセットも，ある意味ではMEスケールであることが知られています．例えば，ダイアトニックスケールはPC空間$\bbZ_{12}$における7音MEスケールとして生成できますが，これをさらにPC空間$\bbZ_7$とみなし，その中で3音MEスケールを生成するとメジャーコードやマイナーコードが得られるのです．具体例として，$C$ダイアトニックスケールにおける$C$メジャーコード，$D$マイナーコード，$B$dimコードを生成する方法を書くと，
$$ \bbZ_3 = \{0, 1, 2\} \xrightarrow{J^0_{7, 3}} \{0, 2, 4\} \xrightarrow{J^5_{12, 7}} \{0, 4, 7\} = \mathrm{C}$$
$$ \bbZ_3 = \{0, 1, 2\} \xrightarrow{J^3_{7, 3}} \{1, 3, 5\} \xrightarrow{J^5_{12, 7}} \{2, 5, 9\} = \mathrm{Dm}$$
$$ \bbZ_3 = \{0, 1, 2\} \xrightarrow{J^4_{7, 3}} \{1, 3, 6\} \xrightarrow{J^5_{12, 7}} \{2, 5, 11\} = \mathrm{Bdim}$$
となります（なおCCVより，この3つ以外のspeciesのコードは存在しません）．このように，$J$関数を2回適用することで得られるようなスケールを2次MEセットといいます．
図示するとすれば以下のようになります．
![!FORMULA[305][36709][0]ダイアトニックスケール（薄い灰色）を!FORMULA[306][1261558730][0]とみなすと，!FORMULA[307][36709][0]メジャーコード（濃い灰色）はその中でMEとなる．](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FonvCmJHYyRJki8QL1xpw.png?alt=media)
$C$ダイアトニックスケール（薄い灰色）を$\bbZ_7$とみなすと，$C$メジャーコード（濃い灰色）はその中でMEとなる．
正の整数$0 < e < d < c$は$\gcd (c, d) = \gcd (d, e) = 1$を満たすとし，$m_1 \in \bbZ_d，m_2 \in \bbZ_c$とする．$J^{m_1, m_2}_{c, d, e} (\bbZ_e)$を2次MEセット（2nd-order ME set）という．ただし，
$$ J^{m_1, m_2}_{c, d, e} = J^{m_1}_{c, d} \circ J^{m_2}_{d, e} : \bbZ_e \to \bbZ_c$$
である．
$J^{5, 0}_{12, 7, 3} (\bbZ_3) = J^5_{12, 7} (J^0_{7, 3} (\bbZ_3)) = \{0, 4, 7\} = \mathrm{C}$
$J^{5, 2}_{12, 7, 4} (\bbZ_4) = J^{5}_{12, 7} (J^{2}_{7, 4} (\bbZ_4)) = \{0, 4, 7, 11\} = \mathrm{CM7}$
通常のMEと区別を強調したい場合は，通常のMEなスケールを「1次MEセット」と呼ぶこともあります．
その他の話題
以下では時間の都合上書ききれなかったことをいくつか紹介します．
近年の音階理論の中でも特に重要なのが，(Douthett 2008)で導入されたfiltered-point symmetry（FiPS）です．これはいわば，2次MEセットの自然な拡張である$n$次MEセット$J^{m_1, \dots, m_n}_{c_1, \dots, c_n} (\bbZ_{c_n})$の構成法を図示したものといえます．これについてはDouthett自身やPlotkinらをはじめとする様々な研究者がネオ・リーマン理論やvoice-leading理論と絡めた詳細な研究を行っています．
また，MEの定義についても議論があり，複数の等価な定義が提示されています．そもそもMEがなぜmaximally even（最大限に均等）という名前であるかというと，これは元々ダイアトニックスケールやホールトーンスケール，ペンタトニックスケールといったスケールが$\bbZ_{12}$の円の中でできるだけ均等になるように配置されているという観察を表現する言葉だったからです．とはいえ，ホールトーンスケールのように$c$が$d$の倍数であるときは完全に均等な配置ができるので何の問題もないのですが，そうでない場合，どのように配置すれば$\bbZ_c$上で「できるだけ均等に」配置したことになるのかは明らかではありません．以下はいずれも$\bbZ_{12}$上に7音スケールを配置した例ですが，(a)と(b)では確かに(b)の方がより均等であるように見えるものの，なぜかと問われると「何となくそう見える」という域を出ないのではないでしょうか．
![!FORMULA[322][-2099443194][0]上に7音スケールを配置した例．(b)はダイアトニックスケール．](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FlVIKRrEhP6CQCflVNr9m.png?alt=media)
$\bbZ_{12}$上に7音スケールを配置した例．(b)はダイアトニックスケール．
さてこの本義に照らすと，ここで紹介したMEの定義はあまり直観的でないことが分かります．スケール内で作れる音程が必ず1種類または半音だけ異なる2種類であることと，スケールができるだけ均等であることとの関係はあまり見えてきません．これはMEが初めて定義された(Clough and Douthett 1991)における定義なのですが，このギャップに応えるため，(Quinn 2004)や(Amiot 2007)では，離散フーリエ変換を用いたより自然な定義が提案されています．また，(Douthett and Krantz 2007)では重み付け関数を用いた定義が提案され，これと関連して1次元反強磁性イジング模型などの物理学上の話題も同時に扱われています．もちろん，これらの定義は全て等価であることが示されています．
また近年では，語の組合せ論を応用したスケールやモードの研究も発達しています．これについては(Clampitt 2019)が詳しいサーベイとなっています．
最後に，この並びに書くのもどうかと思いますが，筆者がまだ証明できていない予想を載せて終わりにします．
$(J^m_{c, d})^{-1} \circ J^m_{c, d} (x) = x$である．ただし，
$$ (J^m_{c, d})^{-1} : x \mapsto \left( \left\lceil \frac{d x - m}{c} \right\rceil \right)_d$$
少なくとも$c = 12$の場合常に正しいことは確認済みですが，まだ任意の正の整数$c$に対する証明が得られていません．もし証明された場合はお知らせいただけると嬉しいです．
おわりに
この記事では，ME，Myhill性，WF，CVといった'90年代までの音階理論で得られているような古典的な話題のみを主に紹介しました．同時に，音階理論は21世紀以降も進歩し続けている分野であり，ここでは紹介しませんでしたが，ネオ・リーマン理論／voice-leading理論／幾何学的音楽理論といった周辺理論との関連付けや，新しい概念・手法の導入などが数多く行われています．
ちなみにこの分野の代表的な研究者であったCloughとDouthettはいずれも既に故人となっており（2003年・2021年），個人的な感想ですが，音階理論もいよいよ新興の分野ではなくなってきたのだなあという事実をしみじみと感じています．
参考文献
- JMM: Journal of Mathematics and Music
- JMT: Journal of Music Theory
- Amiot, Emmanuel. (2007). David Lewin and Maximally Even Sets. JMM, 1(3), 157-172.
- Carey, Norman & Clampitt, David. (1989). Aspects of Well-Formed Scales. Music Theory Spectrum, 11(2), 187-206.
- Carey, Norman & Clampitt, David. (1996). Self-Similar Pitch Structures, Their Duals, and Rhythmic Analogues. Perspectives of New Music, 34(2), 62-87.
- Clampitt, David. (2007). The Legacy of John Clough in Mathematical Music Theory. JMM, 1(2), 73-78.
- Clampitt, David. (2008). “Cardinality Equals Variety for Chords” in Well-Formed Scales, with a Note on the Twin Primes Conjecture. In: (Douthett, Hyde and Smith 2008).
- Clampitt, David. (2019). An Overview of Scale Theory via Word Theory: Notes and Words, Commutativity and Non-Commutativity. MusMat: Brazilian Journal of Music and Mathematics, 3(2), 1-17.
- Clough, John & Douthett, Jack. (1991). Maximally Even Sets. JMT, 35(1/2), 99-173.
- Clough, John & Myerson, Gerald. (1985). Variety and Multiplicity in Diatonic Systems. JMT, 29(2), 249-270.
- Clough, John & Myerson, Gerald. (1986). Musical Scales and the Generalized Circle of Fifths. The American Mathematical Monthly, 93(9), 695-701.
- Douthett, Jack. (2008). Filtered Point-Symmetry and Dynamical Voice-Leading. In: (Douthett, Hyde and Smith 2008).
- Douthett, Jack; Hyde, Martha M. & Smith, Charles J. (2008). Music Theory and Mathematics: Chords, Collections, and Transformations. University of Rochester Press.
- Douthett, Jack & Krantz Richard. (2007). Maximally Even Sets and Configurations: Common Threads in Mathematics, Physics, and Music. Journal of Combinatorial Optimization, 14 (4), 385-410.
- Harasim, Daniel; Schmidt Stefan E. & Rohrmeier, Martin. (2020). Axiomatic Scale Theory. JMM, 14(3), 223-244.
- Hook, Julian. (2023). Exploring Musical Spaces: A Synthesis of Mathematical Approaches. OUP.
- Montiel, Mariana & Peck, Rober W. (Eds.). (2019). Mathematical Music Theory: Algebraic, Geometric, Combinatorial, Topological and Applied Approaches to Understanding Musical Phenomena. World Scientific.
- Plotkin, Richard. (2019). Chord Proximity, Parsimony, and Analysis with Filtered Point-Symmetry. Music Theory Online, 25(2).
- Quinn, Ian. (2004). A Unified Theory of Chord Quality in Equal Temperaments. Ph.D. Thesis, Eastman School of Music.
- Yust, Jason. (2022). Jack Douthett and Mathematical Music Theory. JMM, 16(3), 249-252.
この記事を高評価した人
この記事に送られたバッジ
投稿者
