3
現代数学
文献あり

層の特殊化と超局所化

代数解析,層理論,超局所層理論
716
0
$$\newcommand{bbC}[0]{\mathbb C} \newcommand{bbN}[0]{\mathbb N} \newcommand{bbR}[0]{\mathbb R} \newcommand{bbZ}[0]{\mathbb Z} \newcommand{bfk}[0]{\mathbb{k}} \newcommand{C}[0]{\mathsf{C}} \newcommand{cA}[0]{\mathcal{A}} \newcommand{cB}[0]{\mathcal{B}} \newcommand{Cb}[0]{\mathsf{C}^\mathrm{b}} \newcommand{cC}[0]{\mathcal{C}} \newcommand{cD}[0]{\mathcal{D}} \newcommand{cF}[0]{\mathcal{F}} \newcommand{CF}[0]{\mathrm{CF}} \newcommand{char}[0]{\mathrm{char}} \newcommand{cHom}[0]{\mathcal{H}om} \newcommand{cI}[0]{\mathcal{I}} \newcommand{cJ}[0]{\mathcal{J}} \newcommand{cL}[0]{\mathcal{L}} \newcommand{cM}[0]{\mathcal{M}} \newcommand{Cm}[0]{\mathsf{C}^-} \newcommand{cN}[0]{\mathcal{N}} \newcommand{cO}[0]{\mathcal O} \newcommand{codim}[0]{\operatorname{codim}} \newcommand{Coker}[0]{\operatorname{Coker}} \newcommand{Cp}[0]{\mathsf{C}^+} \newcommand{cRHom}[0]{R\mathcal{H}om} \newcommand{cT}[0]{\mathcal{T}} \newcommand{D}[0]{\mathsf{D}} \newcommand{Db}[0]{\mathsf{D}^\mathrm{b}} \newcommand{DbCc}[0]{\mathsf{D}^\mathrm{b}_{\text{$\mathbb{C}$-c}}} \newcommand{DbRc}[0]{\mathsf{D}^\mathrm{b}_{\text{$\mathbb{R}$-c}}} \newcommand{DbwCc}[0]{\mathsf{D}^\mathrm{b}_{\text{w-$\mathbb{C}$-c}}} \newcommand{DbwRc}[0]{\mathsf{D}^\mathrm{b}_{\text{w-$\mathbb{R}$-c}}} \newcommand{dim}[0]{\operatorname{dim}} \newcommand{Dm}[0]{\mathsf{D}^-} \newcommand{Dp}[0]{\mathsf{D}^+} \newcommand{End}[0]{\operatorname{End}} \newcommand{Eu}[0]{\mathrm{Eu}} \newcommand{Ext}[0]{\operatorname{Ext}} \newcommand{Hess}[0]{\mathrm{Hess}} \newcommand{Hom}[0]{\operatorname{Hom}} \newcommand{IC}[0]{\mathrm{IC}} \newcommand{id}[0]{\mathrm{id}} \newcommand{Image}[0]{\operatorname{Im}} \newcommand{ind}[0]{\mathrm{ind}} \newcommand{Int}[0]{\mathrm{Int}} \newcommand{K}[0]{\mathsf{K}} \newcommand{Kb}[0]{\mathsf{K}^\mathrm{b}} \newcommand{Ker}[0]{\operatorname{Ker}} \newcommand{Km}[0]{\mathsf{K}^-} \newcommand{Kp}[0]{\mathsf{K}^+} \newcommand{KRc}[0]{\mathbf{K}_{\text{$\mathbb{R}$-c}}} \newcommand{lten}[0]{\overset{L}{\otimes}} \newcommand{lto}[0]{\longrightarrow} \newcommand{Mc}[0]{\mathrm{Mc}} \newcommand{Mod}[0]{\operatorname{Mod}} \newcommand{MS}[0]{\operatorname{SS}} \newcommand{MS}[0]{\mathrm{SS}} \newcommand{muDCcge}[0]{{}^\mu\mathsf{D}^{\ge 0}_{\text{$\mathbb{C}$-c}}} \newcommand{muDCcle}[0]{{}^\mu\mathsf{D}^{\le 0}_{\text{$\mathbb{C}$-c}}} \newcommand{Ob}[0]{\mathrm{Ob}} \newcommand{op}[0]{\mathrm{op}} \newcommand{or}[0]{\mathrm{or}} \newcommand{pDCcge}[0]{{}^p\mathsf{D}^{\ge 0}_{\text{$\mathbb{C}$-c}}} \newcommand{pDCcle}[0]{{}^p\mathsf{D}^{\le 0}_{\text{$\mathbb{C}$-c}}} \newcommand{Perv}[0]{\mathrm{Perv}} \newcommand{plushat}[0]{\; \widehat{+} \;} \newcommand{PSh}[0]{\mathrm{PSh}} \newcommand{pt}[0]{\mathrm{pt}} \newcommand{RG}[0]{R\Gamma} \newcommand{RHom}[0]{R\mathrm{Hom}} \newcommand{sgn}[0]{\mathrm{sgn}} \newcommand{Sh}[0]{\mathrm{Sh}} \newcommand{simto}[0]{\overset{\sim}{\to}} \newcommand{supp}[0]{\operatorname{supp}} \newcommand{Supp}[0]{\operatorname{Supp}} \newcommand{tl}[0]{\widetilde} \newcommand{toone}[0]{\overset{+1}{\to}} \newcommand{tr}[0]{\mathrm{tr}} $$

この節では$\mu hom$の構成に向けて，層の特殊化と超局所化という操作を導入します．雑に言うと，特殊化は無限小の錐状集合上の切断を与える層であって，超局所化はマイクロ台を考えたときに出てくる超局所的な障害を与える層のことです．これらはある意味で双対の関係にあって，これはFourier-Sato変換という操作で結びついています．

ここでは最後まで$M$を$X$の余次元$l$の閉部分多様体として，$i \colon M \hookrightarrow X$で埋め込みをあらわします．このとき，$\tau \colon T_MX \to X$で法束をあらわします．記号を増やさないために$\pi$で射影$T^*X \to X$の他にも余法束からの射影$T^*_MX \to M$をあらわします．

層の特殊化

層の特殊化は$X$上の層から法束$T_MX$上の層を作り出す操作です．これによって層$F$が与えられたときに，$M$の法方向に無限小の意味で錐状になっている開部分集合$U$（図3を参照）をわたる切断$F(U)$の帰納極限を層として表示することができます．層の特殊化は法変形（または法束への変形）と呼ばれる幾何学的な構成を通して定義されます．

法変形（法束への変形）

ここでは次の条件を満たす多様体$\widetilde{X_M}$と二つの多様体の射$t \colon \widetilde{X_M} \to \bbR, p \colon \widetilde{X_M} \to X$の三つ組みを構成します：
(1) $t^{-1}(\bbR \setminus \{0 \}) \simeq X \times (\bbR \setminus \{0\})$,
(2) $t^{-1}(0) \simeq T_M X$,
(3) $p^{-1}(X \setminus M) \simeq (X \setminus M) \times (\bbR \setminus \{0\})$.

この$\widetilde{X_M}$は局所的に構成して，それらを適当な変換で貼り合わせることによって得られます．まず局所的なモデルとして$X=\bbR^d$で$M=\{ x=(x',x'') \mid x'=(x_1,\dots,x_l)=\{0\}^l \}$の場合を考えます．このときは，
$$ \widetilde{X_M}:=\{ (x,t) \in \bbR^d \times \bbR \}, t \colon (x,t) \mapsto t, p \colon (x,t) \mapsto (tx',x'') $$
と定めれば条件を満たします．一般の場合は次のように局所的なモデルを貼り合わせます．$M=\bigcup_i U_i$と開埋め込み$\phi_i \colon U_i \to \bbR^d$で$U_i \cap M=\phi_i^{-1}(\{0\}^l \times \bbR^{d-l})$となるものを取ります．そして
\begin{align} & V_i:=\{ (x,t) \in \bbR^d \times \bbR \mid (tx',x'') \in \phi_i(U_i) \}, \\ & t_{V_i} \colon V_i \to \bbR, (x,t) \mapsto t, \ p_{V_i} \colon V_i \mapsto (x,t) \mapsto (tx',x'') \end{align}
と定めます．さらに$\psi_{ji} \colon V_i \times_{U_i} \to (U_i \cap U_j) \to \bbR^d$を
$$ \psi_{ji}(x,t)=(\psi'_{ji}(x,t),\psi''_{ji}(x,t)), \quad (t\psi'_{ji}(x,t),\psi''_{ji}(x,t))=\phi_j \phi_i^{-1}(tx',x'') $$
によって定めます（$t=0$のときは$\phi_j \phi_i^{-1}(tx',x'')$の最初の$l$成分が消滅するので大丈夫）．こうして$(x_i,t_i) \in V_i$と$(x_j,t_j) \in V_j$を$t_i=t_j$かつ$x_j=\psi_{ji}(x_i,t_i)$のとき同一視して貼り合わせると$\widetilde{X_M}$が得られます．また各$V_i$への制限を$t_{V_i}, p_{V_i}$として$t,p$もwell-definedに定めることが出来ます．このように定めると変換関数を調べることで$t^{-1}(0)$が法束$T_MX$と同形になることがチェックできます．

法変形

上で構成した$\widetilde{X_M}$を$X$の$M$への法変形 (normal deformation) または法束への変形 (deformation to normal bundle) と呼ぶ．

以下の図1は法変形の模式的な図です．$x \in X \setminus M$に対してファイバー$p^{-1}(x)$は$T_MX$の無限遠の方に飛んでいきます．
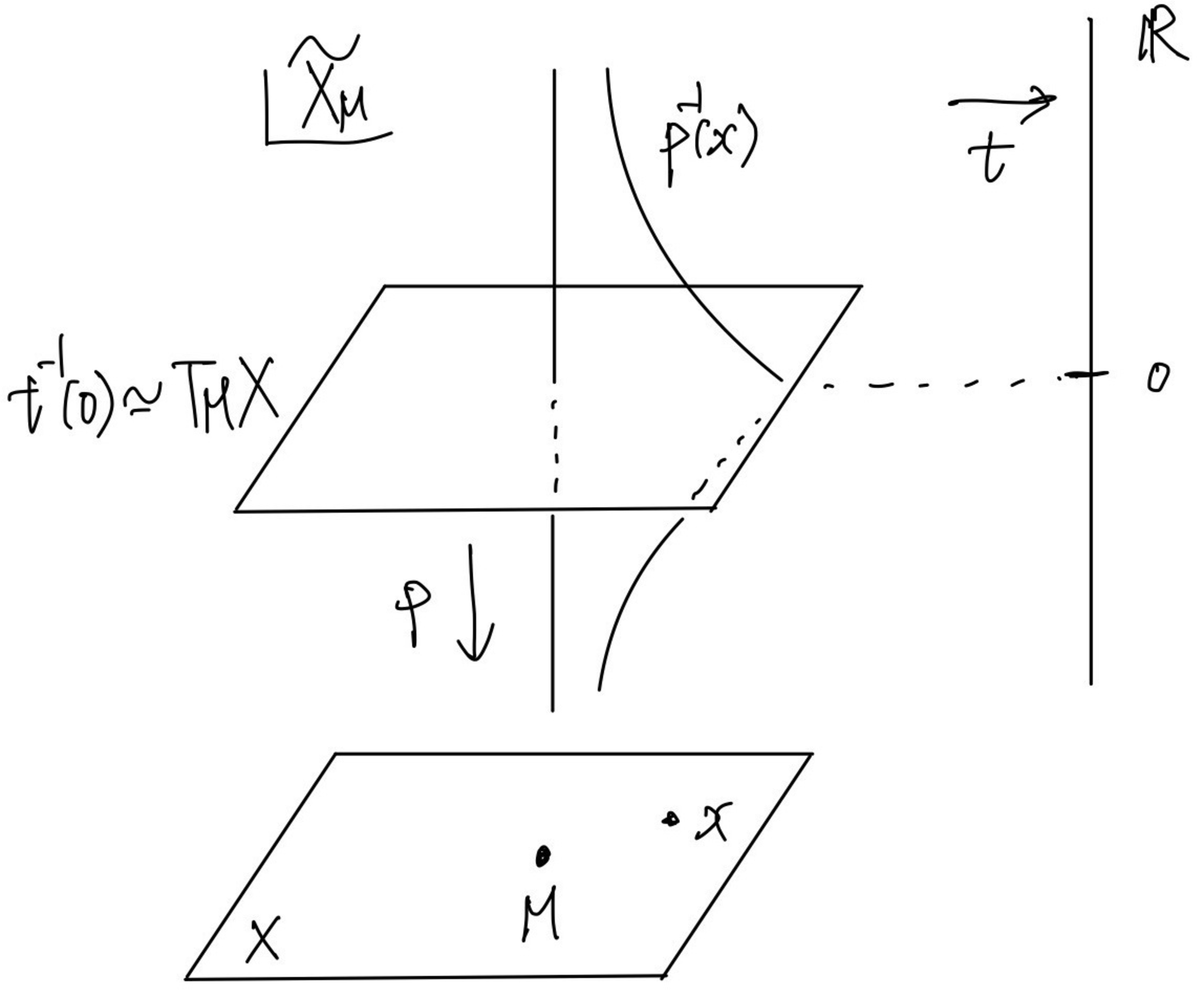法変形の模式図 法変形の模式図

ここで得た法変形はFultonのIntersection theoryなどに載っている代数幾何的な法束への変形の実多様体版とみなすことができます．

さて，法変形を使って$M$の近傍で法方向に無限大に引き伸ばす操作を考えてみましょう．$\Omega:=t^{-1}((0,+\infty))$を$\widetilde{X_M}$の開部分集合として$j \colon \Omega \hookrightarrow \widetilde{X_M}$で埋め込みをあらわし，$\tilde{p}:=p \circ j \colon \Omega \to X$と定めます．$s \colon T_MX =\{t=0\} \hookrightarrow \widetilde{X_M}$で法束の埋め込みをあらわします．すると次の多様体の可換図式が得られます：
$$ \xymatrix{ T_M X \ar@{^{(}->}[r]^-{s} \ar[d]_-{\tau} & \widetilde{X_M} \ar[d]^-{p} & \Omega \ar@{_{(}->}[l]_-{j} \ar[ld]^-{\tilde{p}} \\ M \ar[r]_-{i} & X. } $$

法錐

$X$の部分集合$S$に対して，$C_M(S):=T_MX \cap \overline{\tilde{p}^{-1}(S)}=s^{-1}j(\overline{\tilde{p}^{-1}(S)}) \subset T_M X$と定めて，$C_M(S)$を$M$に沿った$S$の法錐と呼ぶ．

上の模式図でも見たように$M$の近くで法方向に$S$を無限大に引き伸ばしたものが法錐$C_M(S)$になるわけです（図2も参照）． 第3節 の包合性のところで出てきた$C_p(S)$はこれのことでした．図を見れば$S$が部分多様体なら$C_p(S)$が接束$T_pS$になることも理解できると思います．
法錐の模式図 法錐の模式図

特殊化

さて上の法束の構成と似た操作を層に対して行ったものが特殊化です．すなわち$X$上の層$F$を$M$の法方向には無限大に引き伸ばして法束$T_MX$上の層に変換したものです．実は$F \in \Db(\bfk_X)$に対して，同形$s^{-1}Rj_*\tilde{p}^{-1}F \simeq s^! j_! \tilde{p}^!F$が成り立つことがチェックできるので，これを$M$に沿った特殊化と定めます．

層の特殊化

$F \in \Db(\bfk_X)$に対して
$$ \nu_M(F):=s^{-1}Rj_* \tilde{p}^{-1} \simeq s^! j_! \tilde{p}^! F \in \Db(\bfk_{T_MX}) $$
と定めて，$\nu_M(F)$を$F$の$M$に沿った特殊化 (specialization) と呼ぶ．

特殊化の性質

$F \in \Db(\bfk_X)$とする．
(i) $\nu_M(F) \in \Db(\bfk_{T_MX})$は$T_MX$のファイバーへの$\bbR_{>0}$の作用で不変であって$\Supp(\nu_M(F)) \subset C_M(\Supp(F))$が成り立つ．
(ii) $V$を$T_MX$の錐状開部分集合とすると，$\nu_M(F)$の$V$上の切断は$X$の開部分集合$U$が$C_M(X \setminus U) \cap V=\emptyset$を満たすようにわたる際の$U$上の切断と同形である（図3を参照）．すなわち，同形
$$ H^n(V;\nu_M(F)) \simeq \varinjlim_{U} H^n(U;F) $$
が成り立つ．
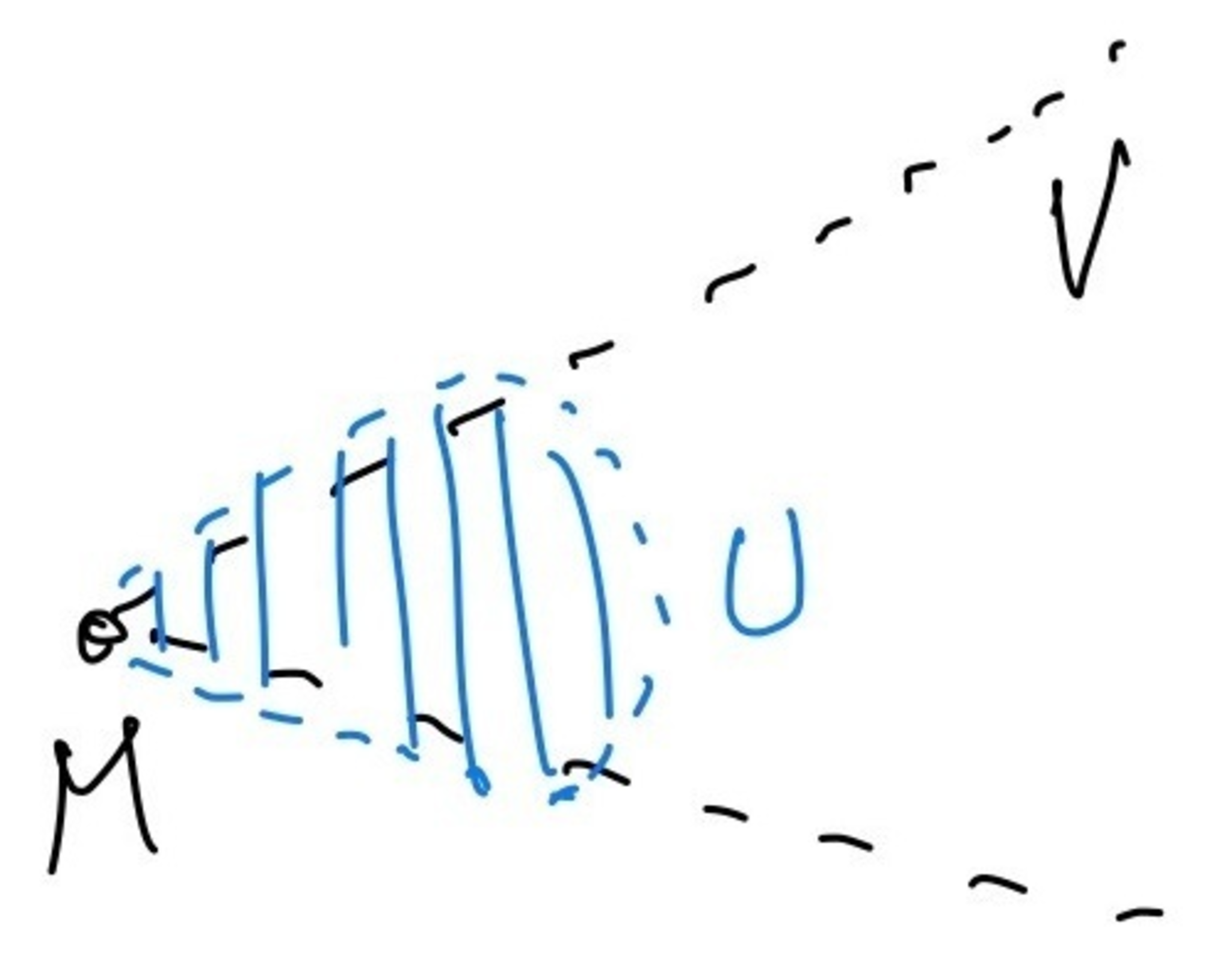条件を満たす開部分集合 条件を満たす開部分集合
(iii) $A$を$T_MX$の錐状閉部分集合とすると，$\nu_M(F)$の$A$に台を持つ大域切断は$X$内の$M$の開近傍$U$と$X$の閉部分集合$Z$が$C_M(Z) \subset A$を満たすようにわたる際の$Z \cap U$に台を持つ$U$上の切断と同形である（図4を参照）．すなわち，同形
$$ H^n_{A}(T_MX;\nu_M(F)) \simeq \varinjlim_{Z,U} H^n_{Z \cap U}(U;F) $$
が成り立つ．
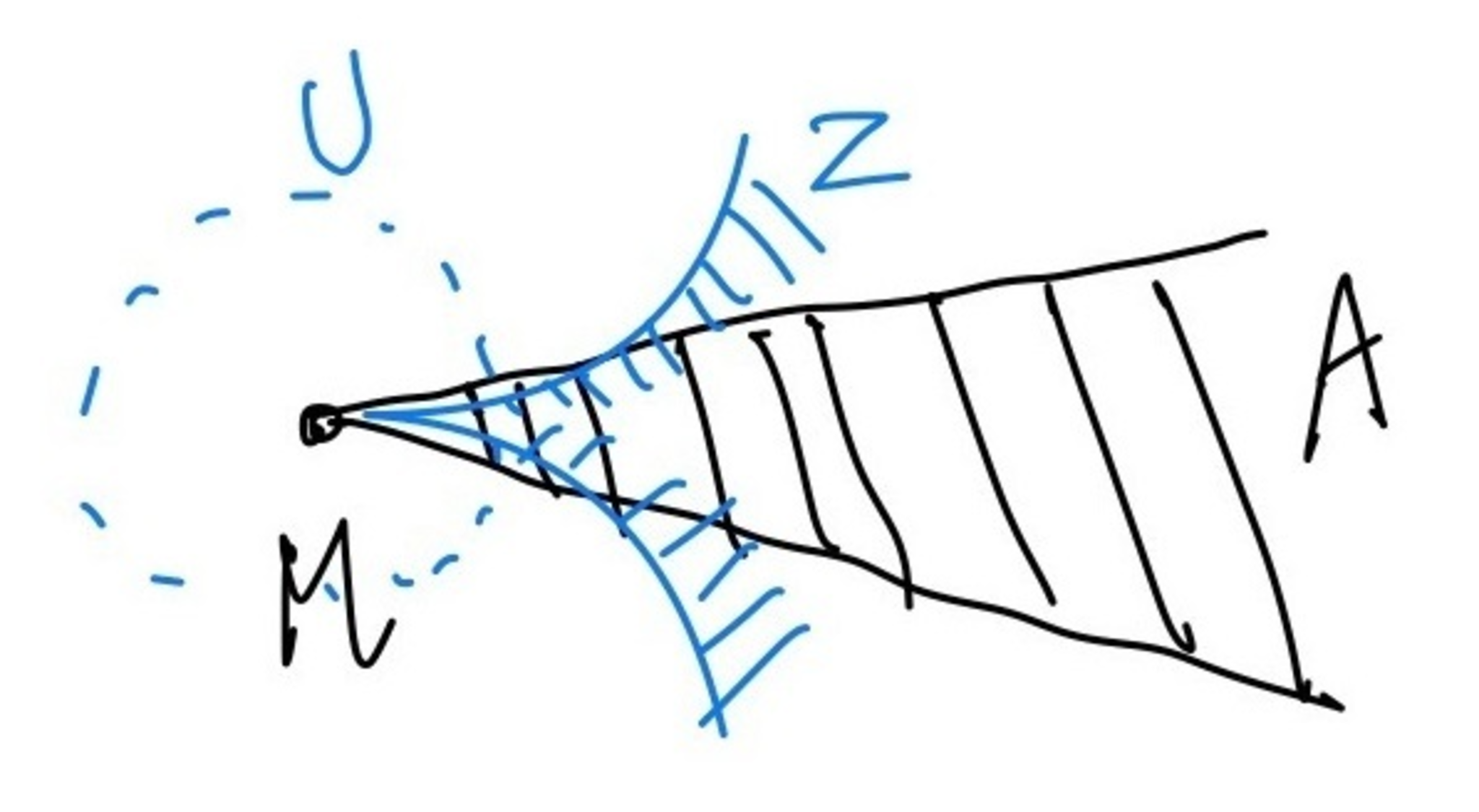条件を満たす閉部分集合と開部分集合 条件を満たす閉部分集合と開部分集合
(iv) 同形
$$ \nu_M(F)|_M \simeq F|_M, \quad \RG_M(\nu_M(F))|_M \simeq \RG_M(F)|_M $$
が成り立つ．ここで$M$は$T_MX$のゼロ切断とみなす．

お気持ち

(i) $\tilde{p}^{-1}F$がの$\bbR_{>0}$の作用で不変なのでよい．
(ii) 上でも述べたように法錐は$M$の近傍で法方向に無限大に引き伸ばしたものなので，$X$の開部分集合$U$が$C_M(X \setminus U) \cap V=\emptyset$を満たしていれば射$\RG(U;F) \to \RG(V;\nu_M(F))$が存在する．あとは帰納極限を取って同形になることを頑張ってチェックすればよい．(iii)は(ii)と五項補題から従う．(iv)は(ii)と(iii)の同形から示すことができる（特殊化の定義における二つのうちいずれかの相性の良い方を使って示すのが簡単）．

正則函数の層の特殊化

$M$を実解析的多様体，$X$をその複素化，$F=\cO_X$を$X$上の正則函数の層とする．このとき，$\nu_M(\cO_X)$は同一視$T_MX \simeq \sqrt{-1}TM$上の層であって，定理1の(ii)から$\sqrt{-1}TM$の錐状開部分集合$V$上の切断が無限小の意味で法方向に$V$だけ開きがある開集合（昔は無限小楔と呼ばれていた）上で正則な函数全体をあらわしている．佐藤超函数は無限小楔上で正則な函数の境界値の和としてあらわされるべきもので（ この佐藤超函数に関する記事 も参照），これを定式化するために佐藤幹夫が初めに特殊化を導入したという歴史がある．

ベクトル空間上の層であって$\bbR_{>0}$によるファイバーへの作用で不変なものはよく出てくるのでその部分圏の記号を定義しておきましょう．ここでも層の複体と層を区別しないで単に層と呼んでしまうことにします．

錐状層

$\tau \colon E \to X$を実ベクトル束とする．このとき，$F \Db(\bfk_E)$が錐状層であるとは任意の$\bbR_{>0}$の軌道$\bbR_{>0}v \ (v \in E)$への制限のコホモロジー層$H^n(F|_{\bbR_{>0}v})$が任意の$n \in \bbZ$に対して定数層になることをいう．$\Db_{\bbR_{>0}}(\bfk_E)$で錐状層からなる$\Db(\bfk_E)$の充満部分圏をあらわす．

この記号を用いると上の定理の(i)は正確には$\nu_M(F) \in \Db_{\bbR_{>0}}(\bfk_{T_MX})$であることを述べています．特殊化は函手$\nu_M \colon \Db(\bfk_X) \to \Db_{\bbR_{>0}}(\bfk_{T_MX})$を定めます．錐状層に対しては次の同形が成り立っていて計算上いろいろと役立つことがあります．つまり錐状層に対しては射影による順像（固有順像）とゼロ切断による逆像（上付きびっくり）が同形になるということです．

錐状層に対する射影とゼロ切断による操作の同形

$\tau \colon E \to X$を実ベクトル束として$i \colon X \to E$でゼロ切断をあらわす．$F \in \Db_{\bbR_{>0}}(\bfk_E)$とする．このとき，同形
$$ R\tau_* F \simeq i^{-1}F, \quad R\tau_!F \simeq i^!F $$
が成り立つ．

この補題を用いると上記定理1の(iv)の同形において同形$R\tau_* \nu_M(F) \simeq \nu_M(F)|_M \simeq F|_M$と$R\tau_!\nu_M(F) \simeq \RG_M(\nu_M(F))|_M \simeq \RG_M(F)|_M$が得られます（$i^! \simeq i^{-1} \circ \RG_X$であったことを思い出しましょう）．

多様体の射に対して順像・逆像に関する特殊化の函手的性質も得られますが，ここでは省略します．

Fourier-Sato変換

函数に対する普通のフーリエ変換は$\bbR^n_x$上の函数を周波数空間$\bbR^n_\omega$上の函数に変換するもので，定数倍（と変数の線形変換）を除いて
$$ \hat{f}(\omega):=\int_\bbR f(x) e^{-\sqrt{-1} \langle x, \omega \rangle} dx $$
で定義されたのでした．これは$\bbR^n_x \times \bbR^n_\omega$上の函数$e^{-\sqrt{-1} \langle x, \omega \rangle}$を核函数とした積分変換で，適当な意味で$\bbR^n_x$上の函数と$\bbR^n_\omega$上の函数の一対一対応を与えていました．この対応の層理論における類似物は色々と考えられていますが，ここではベクトル束$E$上の錐状層の圏とその双対ベクトル束$E^*$上の錐状層の圏との間の圏同値を与えるFourier-Sato変換を説明します．あとではFourier-Sato変換は法束$T_MX$上の特殊化を変換して余法束$T^*_MX$上の錐状層を得るために使われます．

$\tau \colon E \to X$を階数$r$の実ベクトル束として，$\pi \colon E^* \to X$でその双対ベクトル束をあらわします．次の引き戻しの図式を考えます：
$$ \xymatrix{ & E \times_X E^* \ar[ld]_-{p_1} \ar[rd]^-{p_2} & \\ E \ar[rd]_-{\tau} & & E* \ar[ld]^-{\pi} \\ & X. & } $$
普通のフーリエ変換との類似で$E \times_X E^*$上の層を使って層の意味での積分変換を考えます．$E \times_X E^*$の二つの部分集合$P_+,P_-$を
\begin{align} P_+ & := \{ (v,\xi) \in E \times_X E^* \mid \langle v, \xi \rangle \ge 0 \}, \\ P_- & := \{ (v,\xi) \in E \times_X E^* \mid \langle v, \xi \rangle \le 0 \} \end{align}
により定めて，$E \times_X E^*$上の層$\bfk_{P_\pm}$を核として使います．つまり$p_1$で$F \in \Db_{\bbR_{>0}}(\bfk_E)$を$E \times_X E^*$に引き戻して$\bfk_{P_-}$をテンソルして$p_2$で固有順像を取ることで$\Db_{\bbR_{>0}}(\bfk_{E^*})$の対象が得られます．$p_1$と$p_2$，$P_-$と$P_+$を入れ替えることによって逆の変換も得られます．$\bfk_{P_\pm}$が通常のフーリエ変換における核函数$e^{\pm \sqrt{-1} \langle x, \omega \rangle}$の類似というわけです．実は$F \in \Db_{\bbR_{>0}}(\bfk_E)$に対して，同形
$$ R{p_2}_! (p_1^{-1}F)_{P_-} \simeq R{p_2}_* \RG_{P_+}(p_2^{-1}F) \in \Db_{\bbR_{>0}}(\bfk_{E^*}) $$
が成り立つことがチェックできます．同様にして$G \in \Db_{\bbR_{>0}}(\bfk_{E^*})$に対して，同形
$$ R{p_1}_! (p_2^!G)_{P_+} \simeq R{p_1}_* \RG_{P_-}(p_2^!G) \in \Db_{\bbR_{>0}}(\bfk_{E}) $$
が成り立ちます．ここで$p_2$は位相的沈めこみなので$p_2^!$は相対向き付け層とシフトを除いて$p_2^{-1}$と一致しています．基本的にはシフトを除いて引き戻し・核函数のテンソル・固有順像の合成で積分変換が行われていると考えてよいです．上の同形の何がうれしいかというと，各同形の左辺はもう一つの同形の式の右辺の随伴であることが分かるということです．

Fourier-Sato変換

$F \in \Db_{\bbR_{>0}}(\bfk_E)$に対して
$$ F^\wedge := R{p_2}_! (p_1^{-1}F)_{P_-} \simeq R{p_2}_* \RG_{P_+}(p_2^{-1}F) \in \Db_{\bbR_{>0}}(\bfk_{E^*}) $$
と定めて，$F^\wedge$を$F$のFourier-Sato変換と呼ぶ．また，$G \in \Db_{\bbR_{>0}}(\bfk_{E^*})$に対して
$$ G^\vee := R{p_1}_! (p_2^!G)_{P_+} \simeq R{p_1}_* \RG_{P_-}(p_2^!G) \in \Db_{\bbR_{>0}}(\bfk_{E}) $$
と定めて，$G^\vee$を$G$の逆Fourier-Sato変換と呼ぶ．

さて，このように変換を定めると上で説明した随伴の関係になっていることを用いて次が示せます．

Fourier-Sato変換はベクトル束とその双対上の錐状層の圏の間の圏同値を誘導

$(\ast)^\wedge \colon \Db_{\bbR_{>0}}(\bfk_{E}) \to \Db_{\bbR_{>0}}(\bfk_{E^*})$と$(\ast)^\vee \colon \Db_{\bbR_{>0}}(\bfk_{E^*}) \to \Db_{\bbR_{>0}}(\bfk_{E})$は圏同値を与え，互いに逆である．

開部分集合上の切断と閉部分集合に台を持つ相対コホモロジーは様々なところで双対の関係になっていました．Fourier-Sato変換によってもこれらが入れ替わるというのが次の命題です．ベクトル束の錐状部分集合が凸であるとは各ファイバーとの共通部分が凸であることをいい，固有であるとは各ファイバーとの共通部分が直線を含まないことをいいます．$E$の部分集合$A$に対して，その双対集合$A^\circ$を
$$ A^\circ := \{ \xi \in E^* \mid \pi(\xi) \in \tau(A), \langle v, \xi \rangle \ge 0 \ (\forall v \in \tau^{-1}\pi(\xi) \cap A) \} $$
によって定めます．$A^\circ$は常に錐状集合になることに注意しましょう．

Fourier-Sato変換と切断の関係

$F \in \Db_{\bbR_{>0}}(\bfk_E)$とする．
(i) $U$を$E^*$の凸開部分集合とすると，同形
$$ \RG(U;F^\wedge) \simeq \RG_{U^\circ}(E;F) $$
が成り立つ．
(ii) $A$を$E^*$の凸固有錐状閉部分集合とすると，同形
$$ \RG_{A}(E^*;F^\wedge) \simeq \RG(\Int (-A^{\circ});F) \otimes \or_{\tau}[-r] $$
が成り立つ．ここで$\or_{\tau}=\or_{E/X}=H^r(\tau^!\bfk_X)$は$\tau \colon E \to X$に関する相対向き付け層である．

層の超局所化

層の超局所化は上でも予告していたように特殊化したものをFourier-Sato変換して余接束に持って行ったものとして定義されます．

層の超局所化

$F \in \Db(\bfk_X)$に対して
$$ \mu_M(F) := \nu_M(F)^\wedge \in \Db(\bfk_{T^*_MX}) $$
と定めて，$\mu_M(F)$を$F$の$M$に沿った超局所化 (microlocalization) と呼ぶ．

Fourier-Sato変換の性質と特殊化の性質から超局所化に関する次の主張が得られます．

超局所化の性質

$F \in \Db(\bfk_X)$とする．
(i) $\mu_M(F) \in \Db_{\bbR_{>0}}(\bfk_{T^*_MX})$.
(ii) $V$を$T^*_MX$の錐状開部分集合とすると，同形
$$ H^n(V;\mu_M(F)) \simeq \varinjlim_{Z,U} H^n_{Z \cap U}(U;F) $$
が成り立つ．ここで$U$は$U \cap M=\pi(V)$を満たす$X$の開部分集合，$Z$は$C_M(Z) \subset V^\circ$を満たす$X$の閉部分集合をわたる．特に$p \in T^*_MX$に対して，同形
$$ H^n(\mu_M(F))_p \simeq \varinjlim_{Z} H^n_Z(F)_{\pi(p)} $$
が成り立つ．ここで$Z$は$C_M(Z)_{\pi(p)} \subset \{v \in (T_MX)_{\pi(p)} \mid \langle v,p \rangle >0 \} \cup \{0\}$を満たす$X$の閉部分集合をわたる．
(iii) $A$を$T^*_MX$の凸固有錐状閉部分集合とすると，同形
$$ H^n_A(T^*_MX;\mu_M(F) \otimes \pi^{-1}\or_{M/X}) \simeq \varinjlim_{U} H^n(U;F) $$
が成り立つ．ここで$U$は$C_M(X \setminus U) \cap \Int(-A^\circ)=\emptyset$を満たす$X$の開部分集合をわたる．
(iv) 同形
$$ R\pi_* \mu_M(F) \simeq \mu_M(F)|_M \simeq \RG_M(F)|_M, \quad R\pi_!\mu_M(F) \simeq \RG_M(\mu_M(F))|_M \simeq F|_M \otimes \omega_{M/X} $$
が成り立つ．ここで$M$は$T^*_MX$のゼロ切断とみなす．

超局所化は函手$\mu_M \colon \Db(\bfk_X) \to \Db_{\bbR_{>0}}(\bfk_{T^*_MX})$ともみなします．上の定理5の(ii)で特殊な場合を考えるとマイクロ台を定義したときに現れた超局所的な障害が出てきます．実際，$\varphi \colon X \to \bbR$を$C^\infty$級函数として$\varphi(x_0)=0$なる点$x_0$において$p=d\varphi(x_0) \neq 0$であるとしましょう．すると$M=\varphi^{-1}(0)$は$x_0$の近傍で$X$の部分多様体となり，$F \in \Db(\bfk_X)$に対して$\mu_M(F)_p$が考えられます．このとき，定理5の(ii)に現れる$Z$の極大なものとして$\{ x \in X \mid f(x) \ge 0 \}$が取れるので
$$ H^n(\mu_M(F))_p \simeq H^n_{\{x \in X \mid \varphi(x) \ge 0 \}}(F)_{\pi(p)} $$
が得られます．この意味で超局所化は方向別の相対コホモロジーを茎として持っている層ということができます．理論を構築するときは族として層を持っていた方がうれしいので超局所化が重宝されるというわけです．

超局所化の台と層のマイクロ台の関係は次のようになっています．証明は基本的には上記定理5の(ii)で見た超局所化の茎の計算によります．

超局所化とマイクロ台

$F \in \Db(\bfk_X)$とする．このとき，
$$ \Supp(\mu_M(F)) \subset \MS(F) \cap T^*_MX $$
が成り立つ．

さて，超局所化に関する有用な完全三角があるのでここで説明しておきます．$\mathring{T}^*_MX$で$T^*_MX$からゼロ切断を除いた空間をあらわし，$\mathring{\pi}:=\pi|_{\mathring{T}^*_MX}$と定めます．すると，完全三角
$$ R\pi \RG_M(\mu_M(F)) \to R\pi_* \mu_M(F) \to R \mathring{\pi}_* \mu_M(F)|_{\mathring{T}^*_MX} \to R\pi \RG_M(\mu_M(F))[1] $$
が得られます．$\mu_M(F) \in \Db_{\bbR_{>0}}(\bfk_{T^*_MX}$であることから補題2と定理5の(iv)を用いると，同形$R\pi \RG_M(\mu_M(F)) \simeq \RG_M(\mu_M(F))|_M \simeq F|_M \otimes \omega_{M/X}$が得られます．$R\pi_*\mu_M(F)$にも定理5の(iv)を用いると，完全三角
$$ F|_M \otimes \omega_{M/X} \to \RG_M(F)|_M \to R \mathring{\pi}_* \mu_M(F)|_{\mathring{T}^*_MX} \to (F|_M \otimes \omega_{M/X})[1] $$
が得られます．しばしば$R \mathring{\pi}_* \cF|_{\mathring{T}^*_MX}$を単に$R \mathring{\pi}_* \cF$と書いてしまいます．

佐藤の完全列

$M$を$n$次元実解析的多様体，$X$をその複素化，$F=\cO_X$を$X$上の正則函数の層として上の完全三角を考えてみる．このとき，$\cO_X|_M$は$M$上の実解析的函数の層$\cA_M$である．さらに$\RG_M(\cO_X)|_M$は次数$n$に集中していて，そのコホモロジー層に相対向き付け層をテンソルした$H^n_{M}(\cO_X)|_M \otimes \or_{M/X}$を$M$上の佐藤超函数の層$\cB_M$と定めた（ 層理論と導来圏第8節 の例3）．ゆえに上の完全三角に向き付け層をテンソルすれば，完全三角
$$ \cA_M \to \cB_M \to R\mathring{\pi}_* (\mu_M(\cO_X) \otimes \pi^{-1}\or_{M/X}) \to \cA_M[1] $$
が得られる．実は$\mu_M(\cO_X)$も次数$n$に集中していることが示せるので，コホモロジー層$H^n(\mu_M(\cO_X) \otimes \pi^{-1}\or_{M/X})$をマイクロ函数の層$\cC_M$と定める．すると佐藤の完全列と呼ばれる層の完全列
$$ 0 \to \cA_M \to \cB_M \to \mathring{\pi}_* \cC_M \to 0 $$
が得られる．この完全列は佐藤超函数が実解析的でない具合をマイクロ函数で$T^*_MX$上で方向別に解析できるということを述べている．歴史的にはこのように佐藤超函数の超局所解析から超局所化という操作が現れたようである．ちなみに$T^*_MX \simeq \sqrt{-1}T^*M$とみなして同形$\cB_M \simeq \pi_* \cC_M$によって$u \in \cB_M(U)$を$\cC(\pi^{-1}(U))$にうつした際の台を$\MS(u)$と書いて佐藤超函数の特異スペクトラムと呼ぶ（第1節の注意（記号と名称について）も参照）．これが層のマイクロ台のアイデアのもとになったものである．

多様体の射に対して順像・逆像に関する超局所化の函手的性質も特殊化のそれを使うと得られますが，ここでは省略します．

まとめ

この節では

  • 法変形・層の特殊化
  • Fourier-Sato変換
  • 層の超局所化

について説明しました．

参考文献

[1]
Masaki Kashiwara and Pierre Schapira, Sheaves on Manifolds, Grundlehren der mathematischen Wissenschaften, Springer, 1988
[2]
Masaki Kashiwara and Pierre Schapira, Categories and Sheaves, Grundlehren der mathematischen Wissenschaften, Springer, 2006
[3]
William Fulton, Intersection Theory (Second edition), Springer, 1998
[4]
Alexandru Dimca, Sheaves in Topology, Universitext, Springer, 2013
[5]
竹内潔, D加群, 共立講座数学の輝き, 共立出版, 2017
[6]
Mark Goresky and Robert MacPherson, Stratified Morse Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Springer, 1988
[7]
John Willard Milnor（著），佐伯修（翻訳），佐久間一浩（翻訳）, 複素超曲面の特異点, シュプリンガー数学クラシックス, 丸善出版, 2012
[8]
Jörg Schürmann, Topology of Singular Spaces and Constructible Sheaves, Monografie Matematyczne, Birkhäuser, 2003
[9]
Pierre Schapira, A short review on microlocal sheaf theory, 閲覧日 2021年3月14日, https://webusers.imj-prg.fr/~pierre.schapira/lectnotes/MuShv.pdf
[10]
Stéphane Guillermou, Sheaves and symplectic geometry of cotangent bundles, 閲覧日 2021年4月10日, https://arxiv.org/abs/1905.07341
[11]
Pierre Schapira, A short review on microlocal sheaf theory, 閲覧日 2021年4月30日, https://webusers.imj-prg.fr/~pierre.schapira/lectnotes/MuShv.pdf
[12]
Marco Robalo and Pierre Schapira, A Lemma for Microlocal Sheaf Theory in the ∞-Categorical Setting, Publications of the Research Institute for Mathematical Sciences, 2018, 379-391
[13]
Stéphane Guillermou and Pierre Schapira, Microlocal theory of sheaves and Tamarkin’s non displaceability theorem, Homological Mirror Symmetry and Tropical Geometry, Lecture Notes of the Unione Matematica Italiana, 2014, pp. 43-85
[14]
David Nadler and Eric Zaslow, Constructible sheaves and the Fukaya category, J. Amer. Math. Soc., 2009, pp. 233-286
[15]
David Nadler, Microlocal branes are constructible sheaves, Sel. Math. New Ser., 2009, pp. 563–619
[16]
Carl McTague, Stratified morse theory, Unpublished expository essay written for Part III of the Cambridge Tripos, 2002
[17]
Masaki Kashiwara and Pierre Schapira, Microlocal Euler classes and Hochschild homology, Journal of the Institute of Mathematics of Jussieu, 2014, pp. 487-516
[18]
Mark Goresky and Robert MacPherson, Intersection homology theory, Topology, 1980, 135-162
[19]
Mark Goresky and Robert MacPherson, Intersection homology II, Inventiones Mathematicae, 1983, 77-129
[20]
Alexander A. Beilinson, Joseph Bernstein, and Pierre Deligne, Faisceaux pervers, Astérisque, 1982
投稿日：2021年7月8日

この本を高評価した人

高評価したユーザはいません

この本に送られたバッジ

バッジはありません。

投稿者

microsupport
microsupport
152
37380
層理論が好きです．広い意味での代数解析についての記事を書いています．

コメント

他の人のコメント

コメントはありません。
読み込み中
microsupport
microsupport

現在のページ

層の特殊化と超局所化
前のページへ
4 / 9
次のページへ
前ページへ
超局所層理論概説の表紙
次ページへ